基于UDKF的非共面陀螺在轨自主标定方法

张晓文，李骥

1. 北京控制工程研究所，北京 100190 2. 空间智能控制技术国家级重点实验室，北京 100190

陀螺是航天器重要的姿态测量敏感器，存在安装误差、常值漂移和刻度因子误差等影响角速度测量精度的参数。这些陀螺参数虽然可以在地面精度标定，但是在航天器入轨之后还会发生变化。因此对于定姿精度要求高的任务，或是需要陀螺独立外推一段时间姿态的任务，有必要对陀螺参数进行在轨标定。常规航天器使用基于星敏和陀螺测量的6阶滤波器同时估计本体姿态和陀螺常值漂移，忽略陀螺安装误差和刻度因子误差。

在NASA的卡西尼探测器上，设计有15阶卡尔曼滤波，对3部正交安装陀螺的常值漂移、安装误差和刻度因子共12个参数进行在轨标定[1-3]。每次标定分别绕本体系三轴旋转±180°，共持续4-5小时。从2002年到2016年，每年至少进行一次标定，其结果显示，安装误差和刻度因子在被标定更新之后保持了良好的稳定性。在2013年，嫦娥三号着陆器成功飞行应用了一种以星敏测量的姿态四元数和陀螺测量的角度增量作为输入，结合姿态机动，利用UD分解卡尔曼滤波(UDKF)在轨标定陀螺组件的常值漂移、安装误差和刻度因子误差的方法[4]。以上两例标定方法的不足之处是要求陀螺组件标称为正交安装，因此限制了其使用范围。出于冗余备份考虑，很多陀螺组件采用3部正交安装陀螺加1部倾斜安装陀螺的构型。在2014年，月地高速再入返回器成功飞行应用了一种基于最小二乘的可对非正交安装陀螺参数在轨标定的方法，通过一段时间的统计得到陀螺等效漂移的均值，实现计算的轻量化[5]。该方法的使用前提条件是星体角速度控制稳定度较高，因此适于用动量轮或控制力矩陀螺控制姿态的航天器，而不适于用喷气控制姿态的航天器。2016-2017年，在NASA的GOES-16卫星上测试验证了一种通过类似正弦抖动激励和傅里叶分析在轨标定陀螺刻度因子的方法[6]。该方法优点是不需要航天器做大角度机动，因此标定期间星上载荷可以正常工作，缺点是未标定陀螺安装。Zhang[7]研究了非正交安装陀螺常值漂移和刻度因子的在轨标定方法，但是未考虑陀螺安装误差。

有些航天器配置有由陀螺和加速度计组成的惯性测量单元。彭惠[8]、王易南[9]、Lu[10]等以星敏和卫星导航接收机作为测量信息来源，将惯性测量单元中陀螺和加速度计的安装误差和刻度因子等参数共同作为状态变量在一个滤波器中进行估计。

现有研究表明，为了保证陀螺在轨标定算法系统可观，需要航天器进行姿态机动。给定姿态机动序列或轨迹，利用奇异值分解[11]、李导数[12]或是分段线性定常系统可观性理论[13][14]等方法可以分析系统可观性，但是分析计算过程不够简洁。

为解决非正交安装陀螺组件在轨标定问题，对现有的正交安装陀螺组件在轨标定方法[4]进行改进和完善，提出一种基于UDKF的非共面安装陀螺组件在轨自主标定方法。首先，建立非共面陀螺定姿误差模型，并以此建立状态方程；然后，通过正交变换建立测量噪声解耦的测量方程；接着，给出从状态变量求解安装误差和刻度因子误差的精确公式；然后，通过公式推导证明原方法[4]是本方法在陀螺组件为正交安装条件下的特例；之后，基于可观性分析给出简洁的系统可观的角速度组合条件；最后通过数学仿真验证本方法的有效性。

1 陀螺参数标定算法

1.1 非共面陀螺定姿误差模型

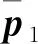
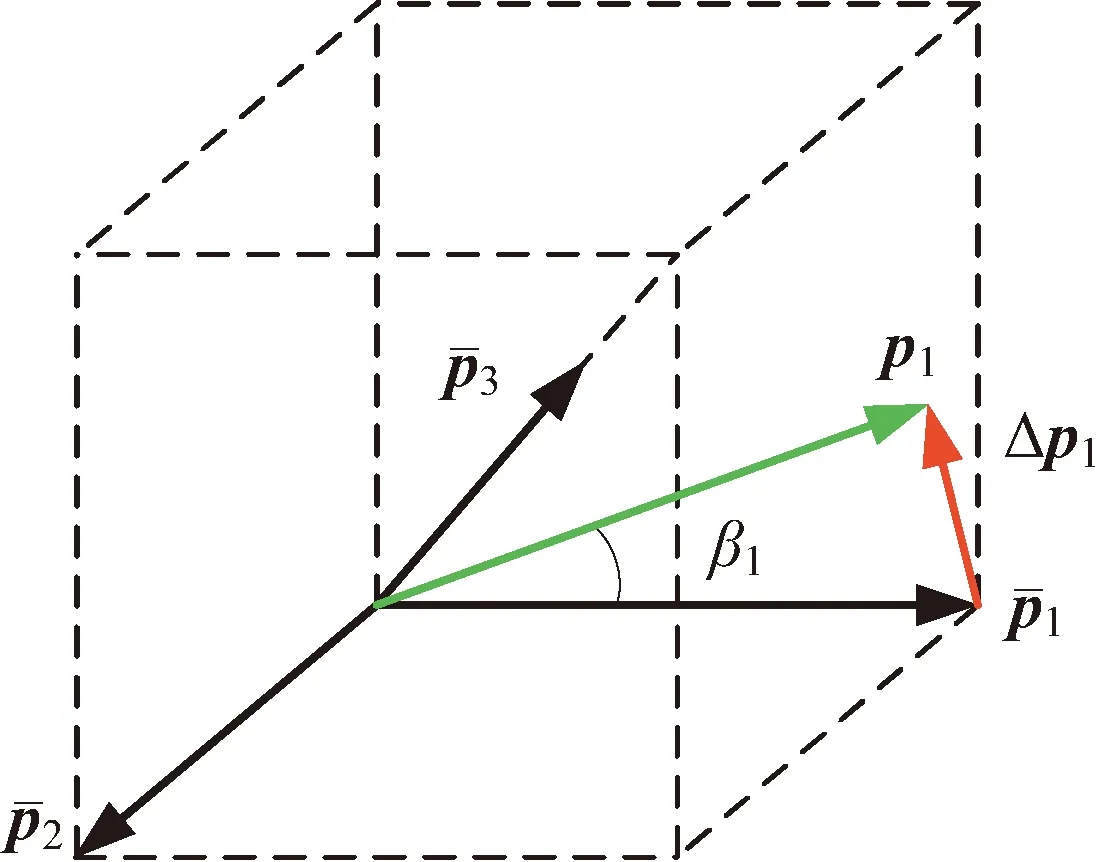
图1 陀螺安装误差示意Fig.1 Gyro misalignment diagram

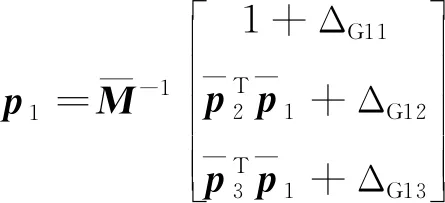
(1)

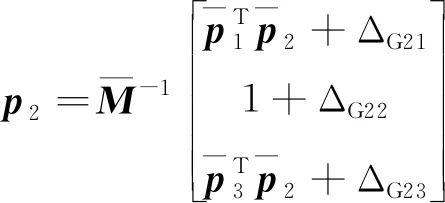
(2)

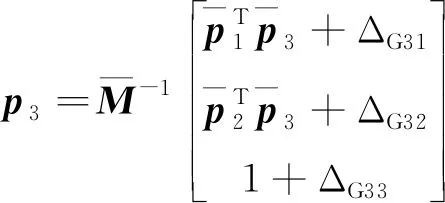
(3)

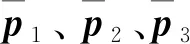
记3个陀螺的刻度因子误差为ΔKGi，常值漂移为bG，测量噪声为nG，则陀螺组件测量的本体角速度的误差为：

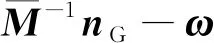
(4)

式中：ω为真实的本体角速度矢量。

定义如下辅助变量：

(5)

则式(4)变为：

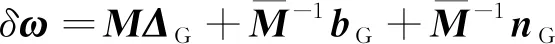
(6)

由式(5)得：

可知，辅助变量ΔG中各元素是陀螺刻度因子误差和安装误差的非线性组合。

在小角度假设下，陀螺定姿误差θ的传播方程为[15]：

(8)

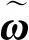
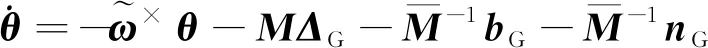
(9)

1.2 滤波器设计

为了提高标定算法的精度，滤波器实际估计的是陀螺常值漂移经过常规方法估计后的残差。这里为了简化表达仍然采用bG来表示。陀螺常值漂移不稳定性建模为：

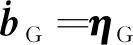
(10)

式中：ηG为随机白噪声。

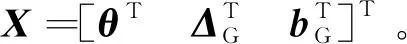
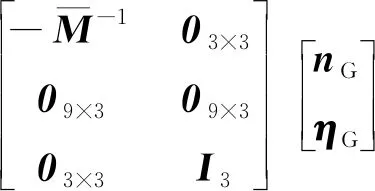
(11)

将星敏测量的本体姿态与陀螺外推的姿态相比较，可得到陀螺定姿误差的测量值，其与真值满足如下关系：

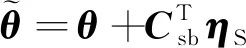
(12)

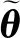
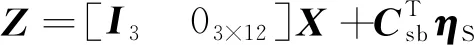
(13)

为保证标定算法的稳定性，滤波器具体实现采用UDKF[16]。UDKF为了序贯处理测量更新，要求测量噪声方差阵为对角阵。为此，将式(13)两边左乘正交阵Csb，得到测量噪声方差阵为对角阵的新的测量方程：

(14)

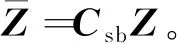
由状态变量定义知，滤波器是直接估计陀螺常值漂移，间接估计陀螺刻度因子误差和安装误差。这里采用间接估计的好处是状态方程为线性。

1.3 UDKF算法

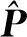
式中:

j=n,n-1,…,2

i=1,2,…,j-1

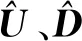
初始化:

α1=r+v1f1

对于j=2,3,…,n,

αj=αj-1+vjfj

最后滤波增益为:

得到滤波增益K后，采用与常规卡尔曼滤波相同公式求取状态变量估计。

1.4 安装误差和刻度因子误差求解

由于滤波器给出的是陀螺安装误差和刻度因子误差的间接估计，即辅助变量ΔG的估计，因此还需要进一步求解。式(5)包含9个方程，而待求解的陀螺参数共有12个，因此不能得出唯一解。如果要得出唯一解，需要增加约束条件。由式(5)得

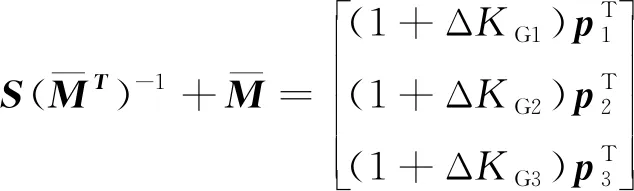
(15)

ΔKGi=‖ei‖-1

(16)

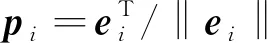
(17)

则陀螺安装误差矢量为：

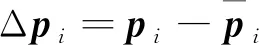
(18)

1.5 正交安装特例

在工程应用中，地面精确标定后的陀螺安装误差角一般不会超过0.1°。以陀螺1为例，当其安装误差角β1取0.1°时，安装误差分量ΔG11约等于1.523×10-6。可见，ΔG11的数值非常小，因此可以忽略。同理ΔG22和ΔG33也可以忽略。此外，再忽略ΔKG1ΔG12等二阶小量，则由式(7)可得陀螺安装误差和刻度因子误差的近似计算公式：

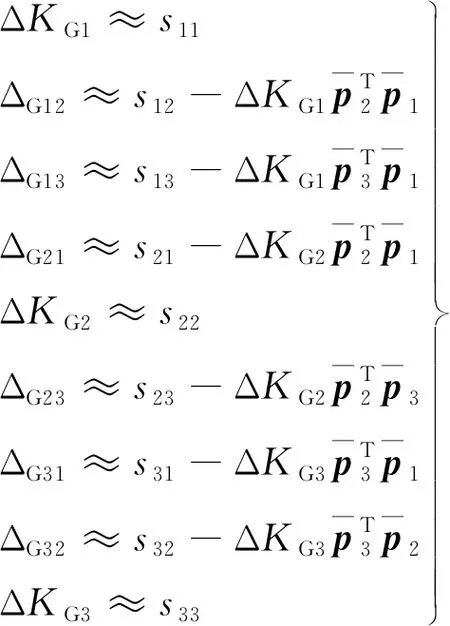
(19)

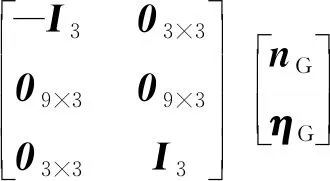
(20)

至此，滤波器的状态变量、状态方程和测量方程与原标定方法[4]相同，因此证明原标定方法是本方法在陀螺组件为正交安装条件下的特例，因此完全可由本方法代替。

2 系统可观性分析

当星体角速度ω为常值时，陀螺测量角速度误差中与安装误差和刻度因子误差相关的项也为常值。它们可以认为是等效的常值漂移，并且可由常规星敏定姿算法估计。以陀螺i为例，若令：

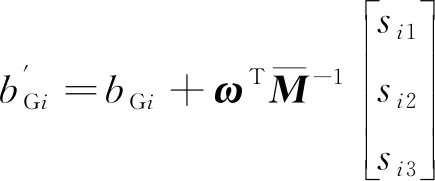
(21)

Axi=bi

(22)

式中：

式(22)有唯一解的条件是：

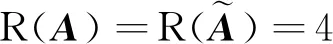
(23)

显然式(23)的成立要求n>3。当n=4时，推导可知式(22)有唯一解的角速度组合条件是：

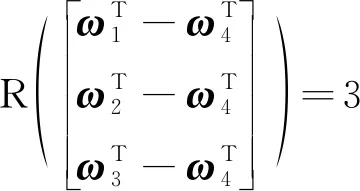
(24)

满足该条件意味着系统输出能够完全反应系统状态，因此式(24)是系统可观的角速度组合条件。不难验证当ω1、ω2和ω3非共面，且ω4为零或-ωi(i=1,2,3)时，式(24)成立。由此可见，航天器绕三个惯量主轴旋转，再加上一个静止状态或是绕一个惯量主轴反向旋转，就可以保证全部状态可观。对于喷气控制的航天器，绕惯量主轴旋转可以提高姿态机动的稳定性。

3 数学仿真结果

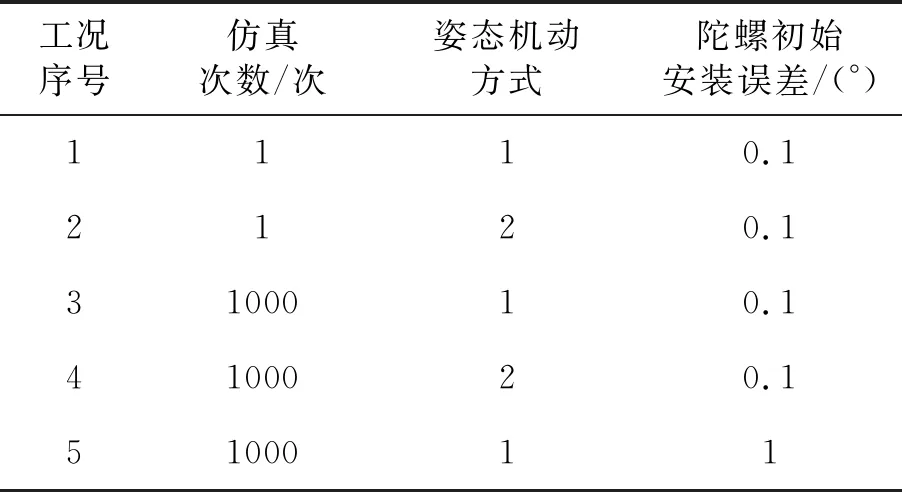
表1 仿真工况列表

工况1的仿真的结果见图2～图4。陀螺安装误差标定结果曲线见图2，在前3个姿态机动段时标定误差较大，在进入第4个姿态机动段时误差迅速减小并收敛。陀螺常值漂移标定结果曲线见图3，在仿真前20 s标定误差变化幅度较大，然后迅速向零附近收敛。陀螺刻度因子标定结果曲线见图4，其变化特点类似安装误差标定结果曲线。陀螺安装误差和刻度因子的标定误差，在前3个姿态机动段，并不一定随着姿态机动段数的增加而减小，但是在进入第4个姿态机动段后都会迅速向零收敛，这与可观性分析结果一致。

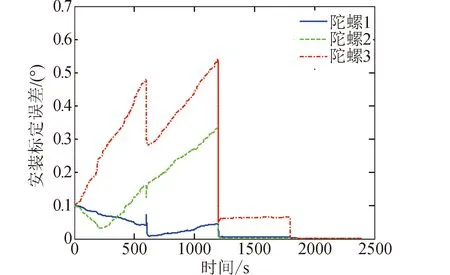
图2 工况1的陀螺安装误差标定结果曲线Fig.2 Calibration error curves of gyro misalignment in case 1

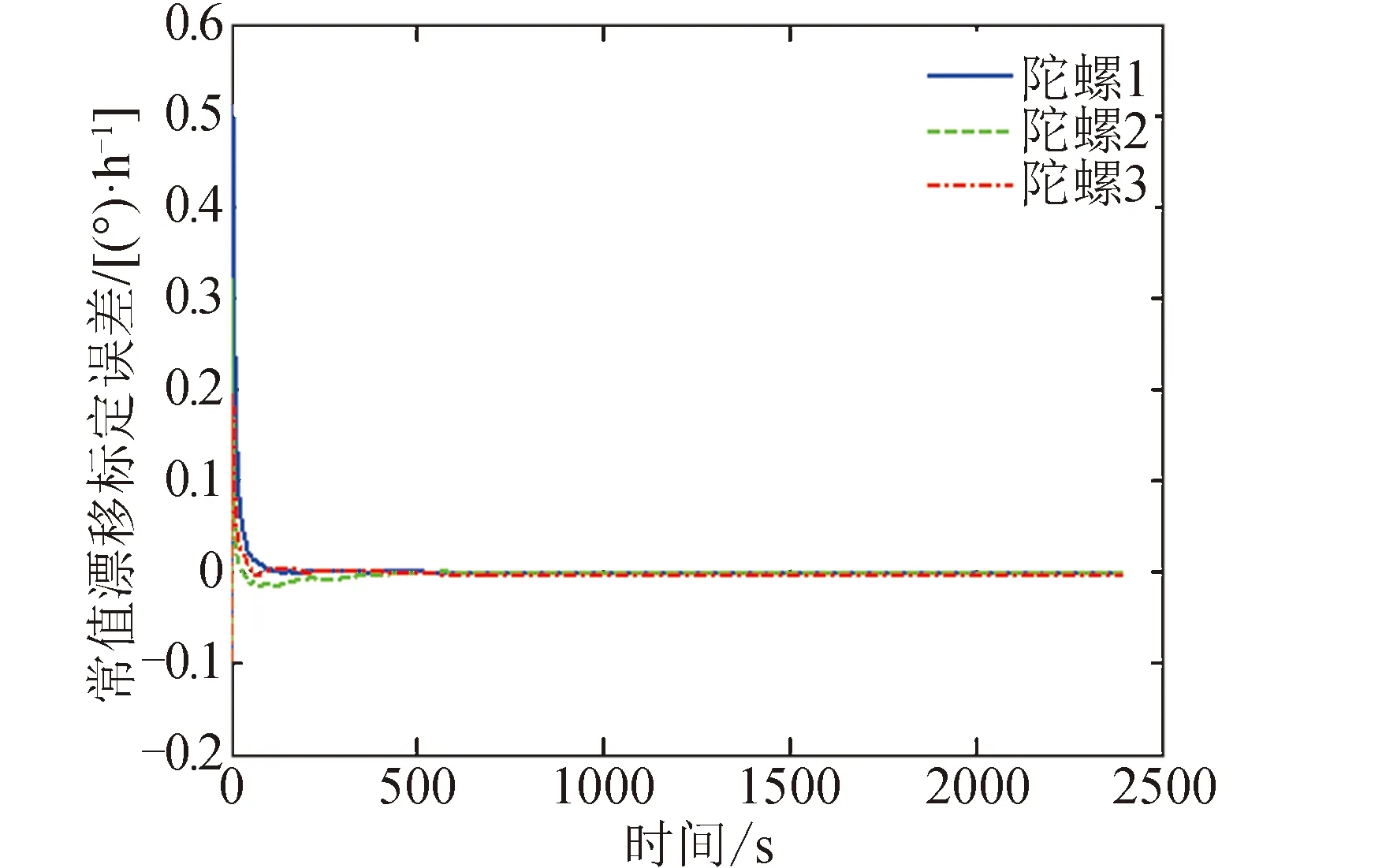
图3 工况1的陀螺常值漂移标定结果曲线Fig.3 Calibration error curves of gyro constant bias in case 1

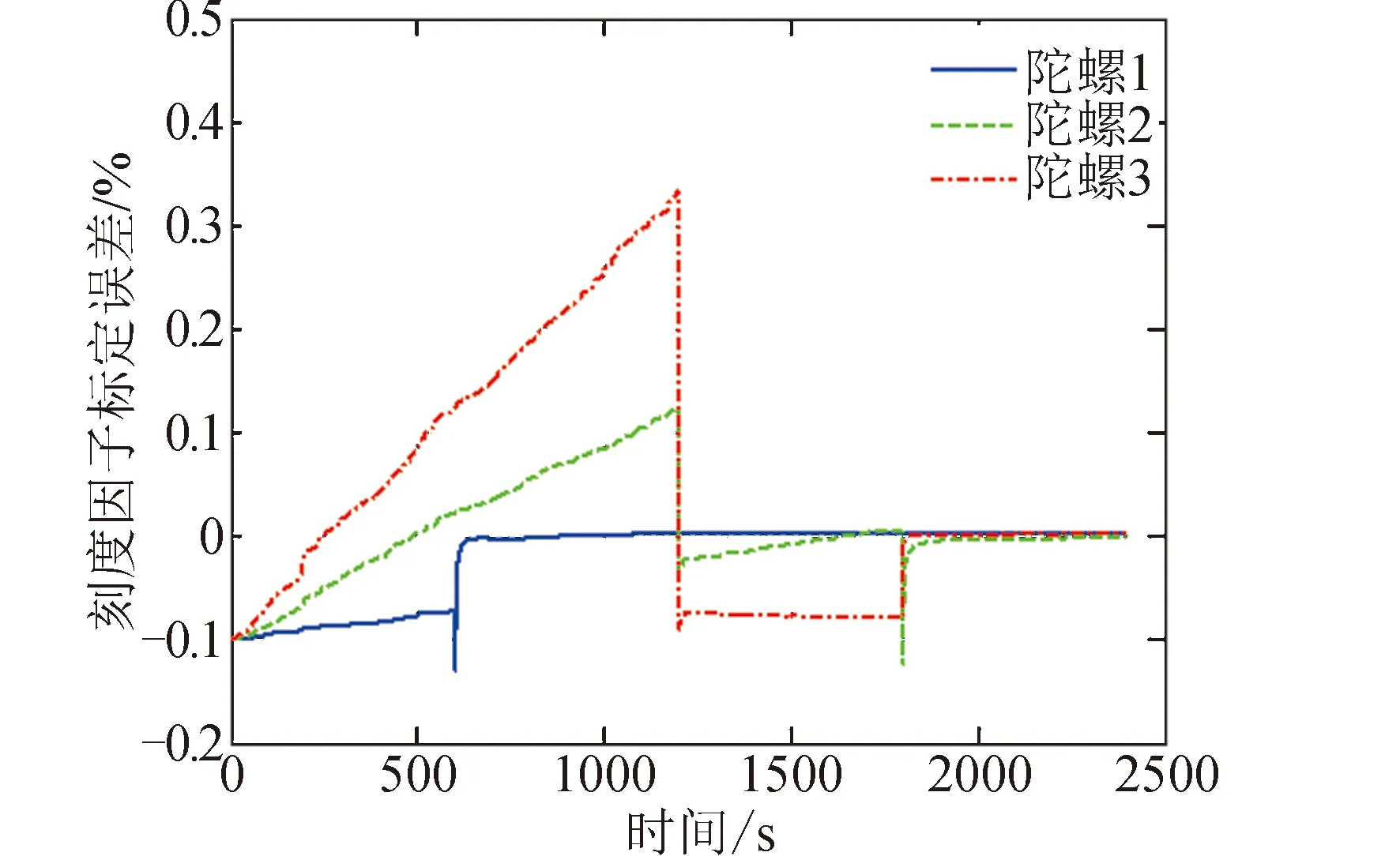
图4 工况1的陀螺刻度因子误差标定结果曲线Fig.4 Calibration error curves of gyro scale factor in case 1

工况2的仿真结果见图5～图7。从图5和图7可知陀螺安装误差和刻度因子的标定误差，在进入第4个姿态机动段后迅速向零收敛。从图6可知陀螺常值漂移的标定误差，在进入第2个姿态机动段后迅速向零收敛，这比工况1要晚。工况2中所有标定误差都能收敛再次验证了可观性分析结果。

图5 工况2的陀螺安装误差标定结果曲线Fig.5 Calibration error curves of gyro misalignment in case 2

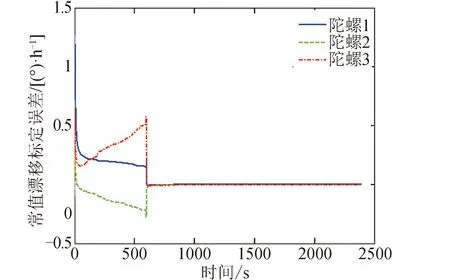
图6 工况2的陀螺常值漂移标定结果曲线Fig.6 Calibration error curves of gyro constant bias in case 2

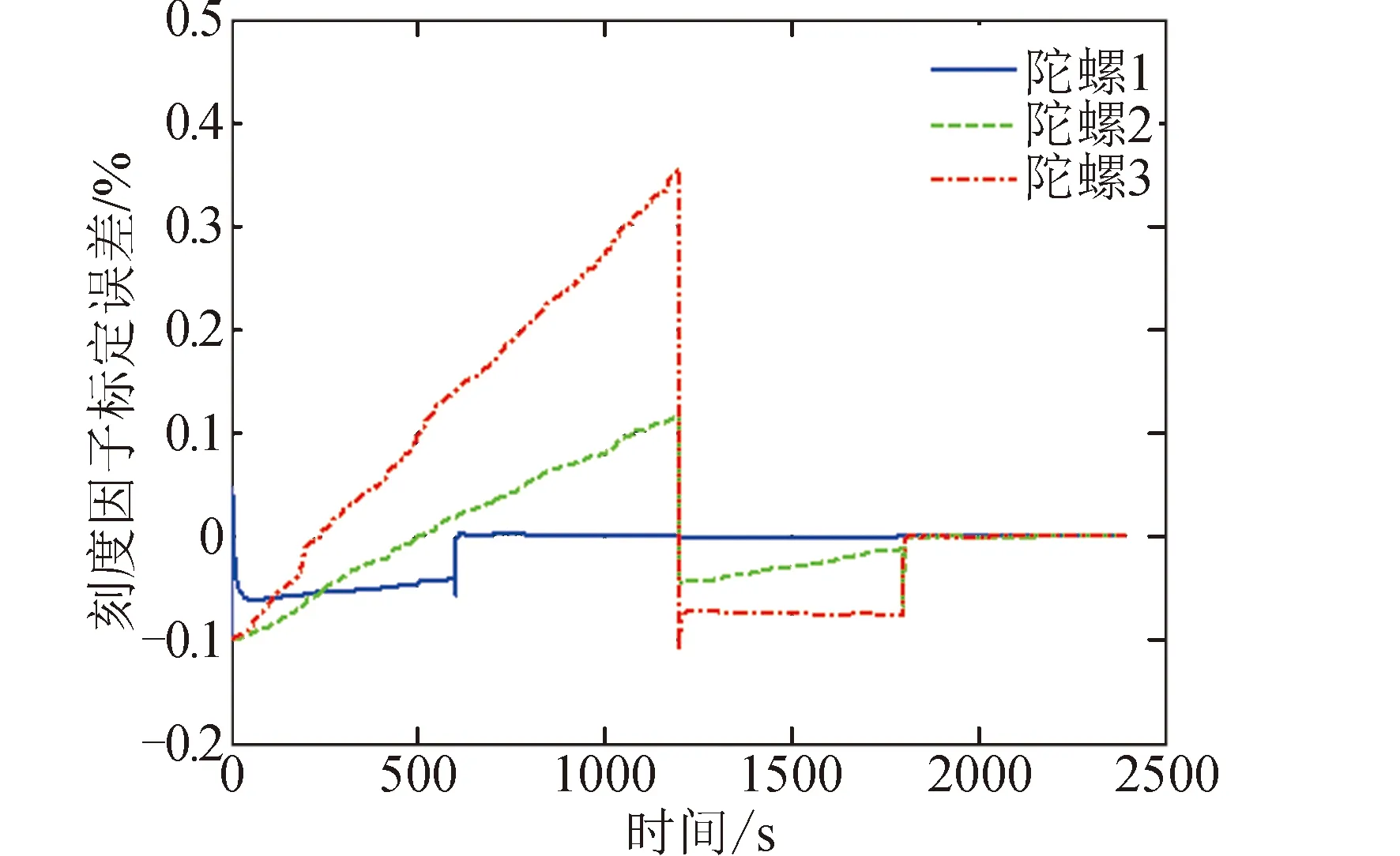
图7 工况2的陀螺刻度因子误差标定结果曲线Fig.7 Calibration error curves of gyro scale factor in case 2

工况3的陀螺参数最大标定误差见表2。陀螺安装误差最大标定误差为0.002 14°，是初始误差的2.14%。陀螺常值漂移最大标定误差为0.00966°/h，是初始误差的9.66%。陀螺刻度因子误差最大标定误差为0.00462%，是初始误差的4.62%。以上数学仿真结果表明本方法有效。

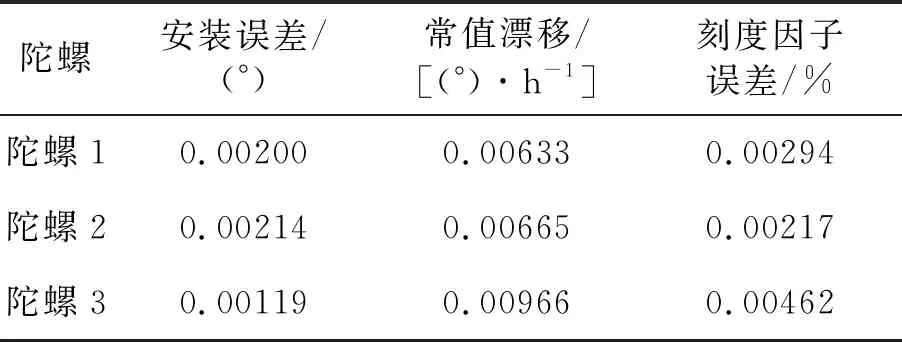
表2 工况3的陀螺参数标定结果

工况4的陀螺参数最大标定误差见表3。陀螺安装误差最大标定误差为0.001 64°，是初始误差的1.64%。陀螺常值漂移最大标定误差为0.00736°/h，是初始误差的7.36%。陀螺刻度因子误差最大标定误差为0.00292%，是初始误差的2.92%。表3结果优于表2结果，说明姿态机动方式2的标定精度高于姿态机动方式1。

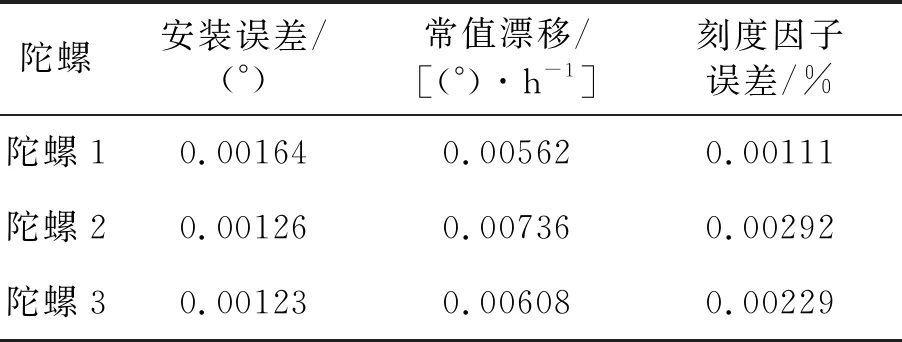
表3 工况4的陀螺参数标定结果

工况5的陀螺参数最大标定误差见表4。

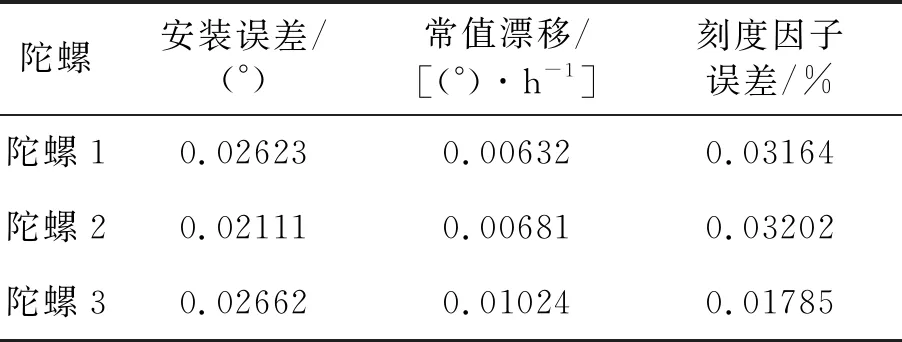
表4 工况5的陀螺参数标定结果

陀螺安装误差和刻度因子误差的最大标定误差相对表2增大一个量级，但是与表2工况的初始误差相比，减小了一个量级。陀螺常值漂移最大标定误差与表2相当。该结果说明陀螺初始安装误差增大，则陀螺安装误差和刻度因子误差的标定误差会增大，而陀螺常值漂移标定误差无显著变化。此外，如果再进行一轮迭代标定，可将标定精度提高到优于表2结果的水平。

4 结束语

对现有的正交安装陀螺组件在轨标定方法进行改进，提出应用范围更为广泛的非共面安装陀螺组件的安装误差、常值漂移和刻度因子误差在轨自主标定方法。该方法不要求陀螺为正交安装，不要求标定姿态机动高稳定度。公式推导证明，原方法是本方法在陀螺组件为正交安装条件下的特例，因此完全可由本方法代替。给出的系统可观的角速度组合条件可指导姿态机动序列的设计工作。数学仿真结果表明本方法有效，陀螺安装误差、常值漂移和刻度因子误差标定精度分别优于0.01°、0.01(°)/h和0.01%。本方法对于有惯性导航需求的航天器设计具有重要的工程应用价值。