微结构固体中孤立波的动力稳定性*

韩元春 那仁满都拉

（内蒙古民族大学数理学院，通辽 028043）

引言

随着科学技术的迅速发展，人们越来越关注微晶、合金、岩石、陶瓷以及功能梯度材料等含微结构的固体材料中波传播问题.这主要是因为当今检测技术中所使用的一些高频波的波长越来越接近材料的微结构特征长度，导致微结构效应对波场产生了不可忽视的影响.由于经典连续介质理论不能对含微结构的固体材料的力学行为给出准确描述，人们提出了若干描述其变形与运动的理论和模型［1-4］.近年来，Engelbrecht等根据Mindlin微结构理论，重点研究了含微结构的固体材料中孤立波的存在与传播问题.在文献［5］中建立了微结构固体的非线性基本模型，并证明了微结构固体中可以存在一种非对称孤立波.文献［6］中详细研究了微结构效应对孤立波的传播及相互作用的影响.文献［7］中研究了微结构固体中孤立波传播的反问题.文献［8］中本文作者之一用定性分析方法证明了微结构固体中对称与非对称孤立波的存在性.

含微结构的固体材料中孤立波的形成与传播问题的研究对该材料的无损检测与评价具有重要意义.因为孤立波在固体材料中传播时，其形状、幅度以及传播速度中携带着材料内部结构特性的重要信息.从文献［7］的研究结果看，这可能成为对固体材料进行检测与评价的一种有效手段.但不管是在实验中，还是在实际检测中，在固体材料中传播的孤立波始终受到不同程度的扰动，所以在扰动影响下孤立波能否稳定传播成为关键问题，只有稳定传播的孤立波，才能克服扰动，能够长时间存在，且能在实验中观测到和实际中应用到.近年来，对复杂系统中孤立波的存在性和动力系统的稳定性问题的研究受到了越来越多的重视［9-12］.

本文以描述微结构固体的一种KdV类方程作为控制方程并利用积分因子方法，将对微结构固体中传播的孤立波在不同小扰动的影响下能否稳定传播问题进行数值模拟研究.

1 波模型及积分因子方法

在文献［13］中建立了描述Mindlin型微结构固体中一维孤立波传播的新模型

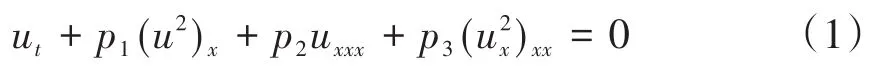
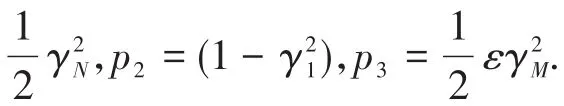
积分因子方法是数值求解偏微分方程的一种计算速度快、精度高、稳定性好并能容易编程实现的有效方法，是属于一种伪谱方法［14，15］.该方法通过作快速傅里叶变换（FFT）和乘积分因子的巧妙手段，消掉方程中导致数值频散的刚性项（即线性空间导数项），从而达到高精度求解方程的目的.依据该方法的基本思想，对方程（1）作傅里叶变换，可得

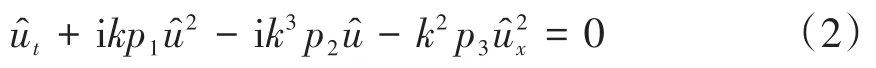
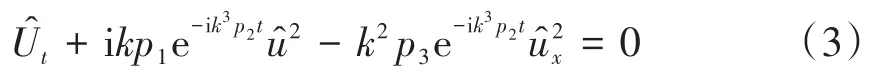
又因为

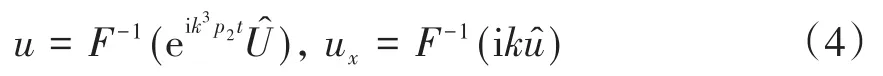
把（4）式代入方程（3），可得

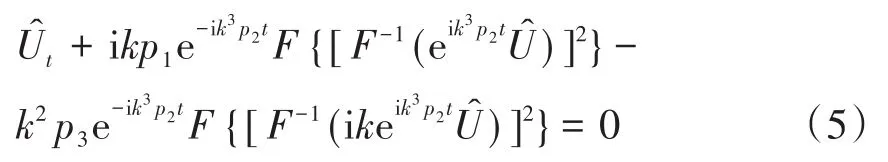
2 微结构固体中孤立波传播的稳定性

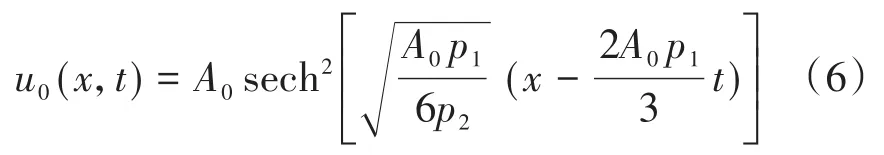
这里常数A0表示孤立波的波幅.式（6）表示一种向右传播的对称钟型孤立波，其传播速度和宽度都与波幅有关，这是非线性波的重要特性.为考察未受扰孤立波在微结构固体中的传播特性，这里以式（6）为初始条件，并采用周期性边界条件，在区间[-π，π]上进行数值计算.计算时选取的材料常数为p1=100，p2=3，p3=0.01，孤立波的幅度为A0=1.图1绘制的是t=0.4时刻在弱微尺度非线性效应的微结构固体中传播的孤立波波形以及此时的孤立波波形与初始波形上对应点的位移偏差（图中用Δu表示偏差）.可看出，随着时间的推移，初始时刻的孤立波（6）缓慢变形并产生了一些偏差，但这种弱微尺度非线性效应下所产生的偏差非常小，即孤立波能够较长时间基本保持波形和传播速度在微结构固体中稳定传播.因此，在弱微尺度非线性效应的微结构固体中孤立波基本能够保持波形和传播速度而较长时间稳定传播.值得注意的是微结构固体中传播孤立波的动力学稳定性与固体介质的材料常数有关，当固体的微尺度非线性效应较强（p3较大）时，微结构固体中的孤立波明显变形、失去其对称性，并形成一种非对称孤立波或根本不能形成孤立波［5，8］.因此，微结构固体中孤立波的形成需要合适的条件，不同的微结构固体（材料常数不同）中形成的孤立波的形状特性不同，其传播的稳定性也应有所不同.

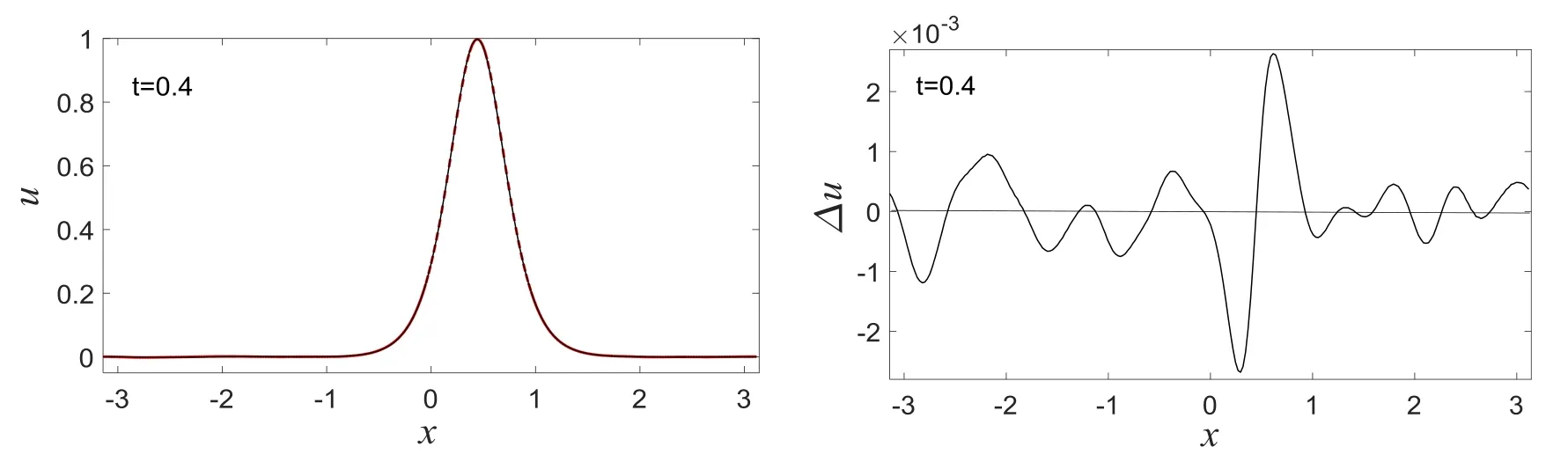
图1 未受扰孤立波（红色虚线）与初始波形的偏差Fig.1 The deviation of undisturbed solitary wave（red dashed line）and initial waveform

2.1 高斯波扰动下的孤立波

假设微结构固体中传播的孤立波受到了高斯波扰动，其表达式为

式中，A为高斯波的幅度，μ为高斯波的宽度因数.数值模拟时，采用周期性边界条件，并在区间[-π，π]上进行计算，初始条件取为u（x，0）=u0（x，0）+u′（x，0），材料常数取为 p1=100，p2=3，p3=0.01，孤立波幅度为A0=1.由于考虑的是小扰动，所以扰动幅度应足够小，取为A=0.01，约为孤立波幅度的1%.如果扰动幅度较大，肯定会影响孤立波的稳定传播，这是众所周知的.一般来讲，经过足够长时间的演化后，如果扰动的幅度没有产生明显的增加，受扰波的波幅、宽度等波形结构和传播速度基本保持不变，则可判定该波是动力学稳定；如果扰动的幅度产生明显的增加，受扰波的波形结构和速度发生明显改变，则可判定该波是动力学不稳定.在图2中显示的是当A=0.01，μ=40时，t=0和t=0.4时刻的孤立波的波形图.可看出，随着时间的推移，初始时刻的局部扰动，逐步弥散到整个计算区域，但扰动幅度没有明显增加.经过一定时间的演化后，t=0.4时刻的受扰孤立波的波形和传播速度有了一些小的变化，出现了一些波尾，在图3所示的受扰孤立波与未受扰孤立波在同一时刻的偏差图上也能看到这一点.这表明微结构固体中的孤立波的抗干扰性不是很强，其动力学稳定性也不是很稳定.特别是当A=0.01，μ=10，即改变局部扰动的宽度时，受扰孤立波的波形结构和传播速度有了比较明显变化（如图4所示），在图5所示的偏差图上也明显看到这一点.这表明高斯波扰动的幅值能够影响孤立波的稳定传播之外，其宽度也能影响孤立波的稳定传播.由此可总结出：微结构固体中传播孤立波的抗干扰性即其动力学稳定性不是很强，只有受到幅度和宽度都非常小的高斯波扰动下，微结构固体中传播的孤立波才能显现出一定程度的动力学稳定性.

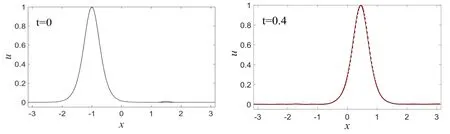
图2 高斯波扰动下的孤立波（红色虚线）Fig.2 The solitary wave（red dashed line）disturbed by Gaussian wave

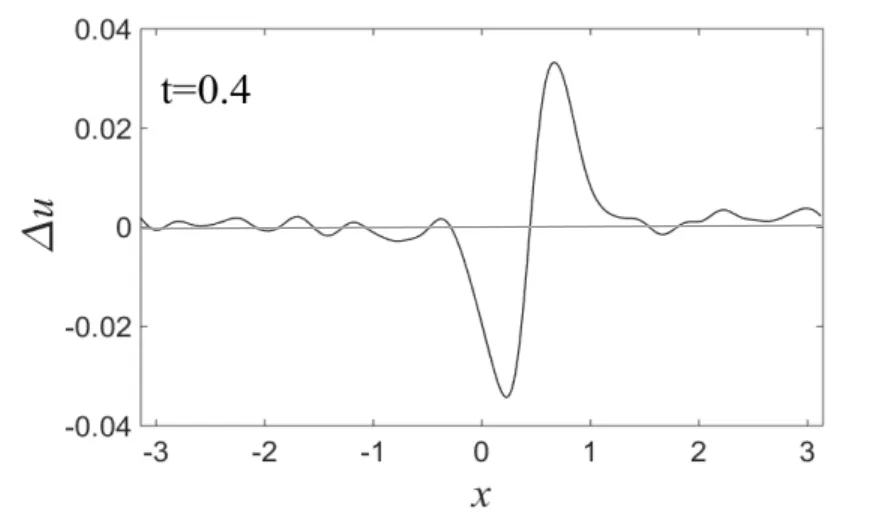
图3 受扰孤立波与未受扰孤立波的偏差Fig.3 The deviation of disturbed solitary wave and undisturbed solitary wave

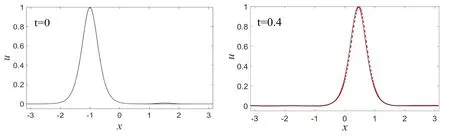
图4 高斯波扰动下的孤立波（红色虚线）Fig.4 The solitary wave（red dashed line）disturbed by Gaussian wave

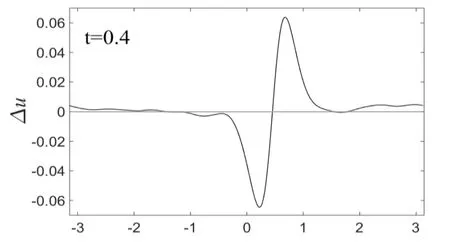
图5 受扰孤立波与未受扰孤立波的偏差Fig.5 The deviation of disturbed solitary wave and undisturbed solitary wave

2.2 Ricker子波扰动下的孤立波

假设微结构固体中传播的孤立波受到了Ricker子波扰动，其表达式为

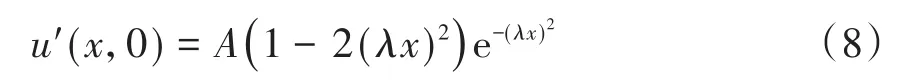
其中，A为Ricker子波的幅度，λ为Ricker子波的宽度因数.数值模拟时，所采用的边界条件、初始条件、材料常数和孤立波幅度都与上节的相同.图6中显示的是当A=0.01，λ=6时，t=0和t=0.4时刻受到Ricker子波扰动的孤立波波形图.由图可看出，随着时间的推移，初始时刻的局部扰动，逐步弥散到整个计算区域，但扰动幅度没有明显增加.经过一定时间演化后，受扰孤立波的波形和传播速度开始发生了一些微小的变化，但还能够保持原有特性.如图7所示的受扰孤立波与未受扰孤立波的偏差图上可以看到两者的偏差，显然偏差度很小.因此，在Ricker子波小扰动下孤立波的波形和传播速度也发生了一些微小的变化，但相比于高斯波扰动下的变化要小一些.当A=0.01，λ=3，即改变局部扰动的宽度时（如图8所示），受扰孤立波的波形和传播速度有了较明显变化（如图9所示）.这表明Ricker子波的宽度也能够影响孤立波的稳定传播.由此可得：微结构固体中传播孤立波的抗干扰性和动力学稳定性不是很强，只有受到幅度和宽度都非常小的Ricker子波扰动下，微结构固体中传播的孤立波才能显现出一定程度的动力学稳定性.

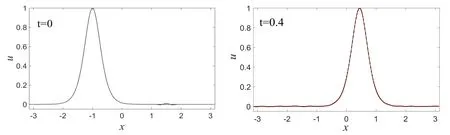
图6 Ricker子波扰动下的孤立波（红色虚线）Fig.6 The solitary wave（red dashed line）disturbed by Ricker wavelet

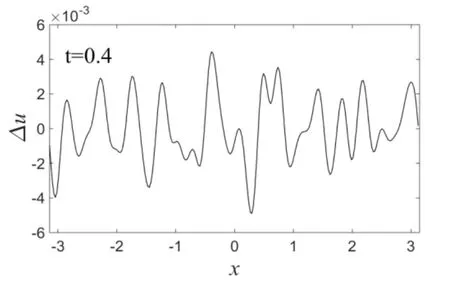
图7 受扰孤立波与未受扰孤立波的偏差Fig.7 The deviation of disturbed solitary wave and undisturbed solitary wave

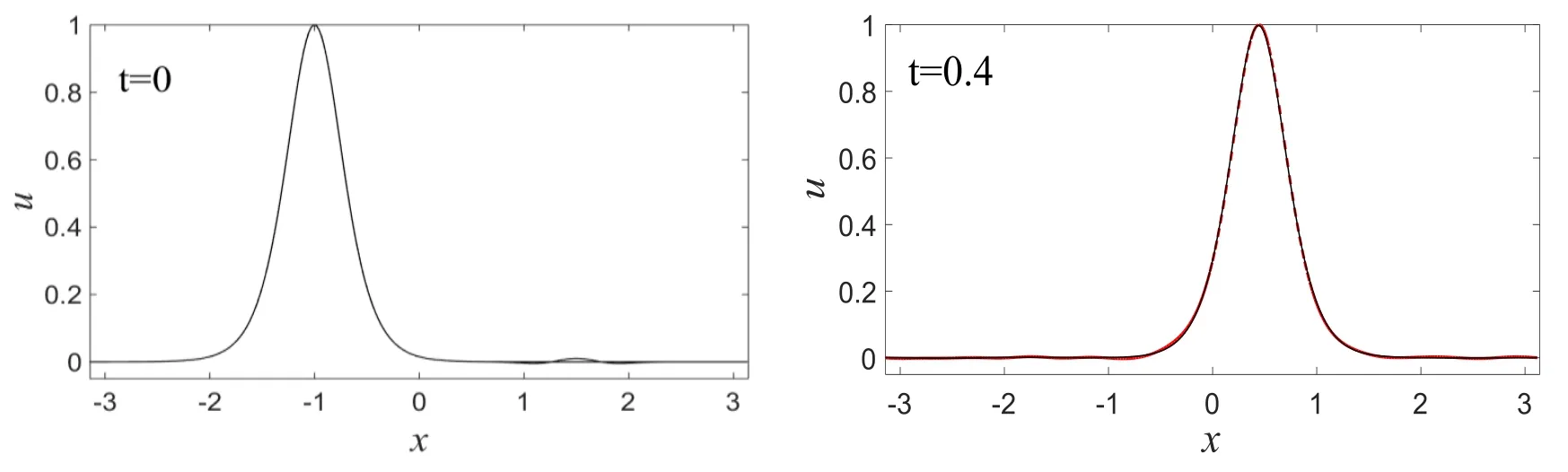
图8 Ricker子波扰动下的孤立波（红色虚线）Fig.8 The solitary wave（red dashed line）disturbed by Ricker wavelet

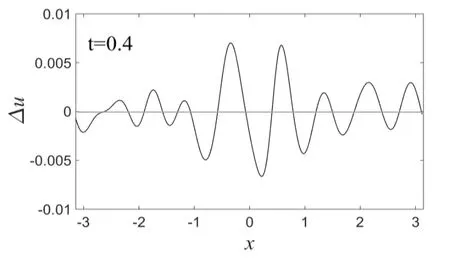
图9 受扰孤立波与未受扰孤立波的偏差Fig.9 The deviation of disturbed solitary wave and undisturbed solitary wave

2.3 双曲正割波扰动下的孤立波

设微结构固体中传播的孤立波受到了双曲正割波小扰动，即 u′（x，0）=Asech（μx），同样我们采用数值方法考察了孤立波传播的动力学稳定性.数值模拟时，所采用的边界条件、初始条件、材料常数和孤立波幅度等都与上节相同.图10给出的是当A=0.01，μ=12时，在t=0和t=0.4时刻受到双曲正割波扰动的孤立波的波形图.图11给出的是在t=0.4时刻受扰孤立波与未受扰孤立波的偏差图.从偏差图可看出，受到双曲正割波扰动的孤立波的波形和传播速度的变化情况非常类似于受到高斯波扰动的孤立波的波形和传播速度的变化情况.图12给出的是当A=0.01，μ=6时，在t=0和t=0.4时刻受到双曲正割波扰动的孤立波的波形图，即受到宽度较宽的双曲正割波扰动的情况.可以看出，受到宽度较宽的双曲正割波扰动之后，孤立波的波形和传播速度有了更明显的变化，从偏差图13也可看到这一点.此时的变化情况非常类似于受到高斯波扰动的孤立波的波形和传播速度的变化情况.相比受到三种不同小扰动下的孤立波的波形和传播速度的变化，可看出在Ricker子波扰动下孤立波的波形和传播速度的变化最小，高斯波扰动和双曲正割波扰动下孤立波的波形和传播速度的变化非常类似，偏差程度也基本相同.

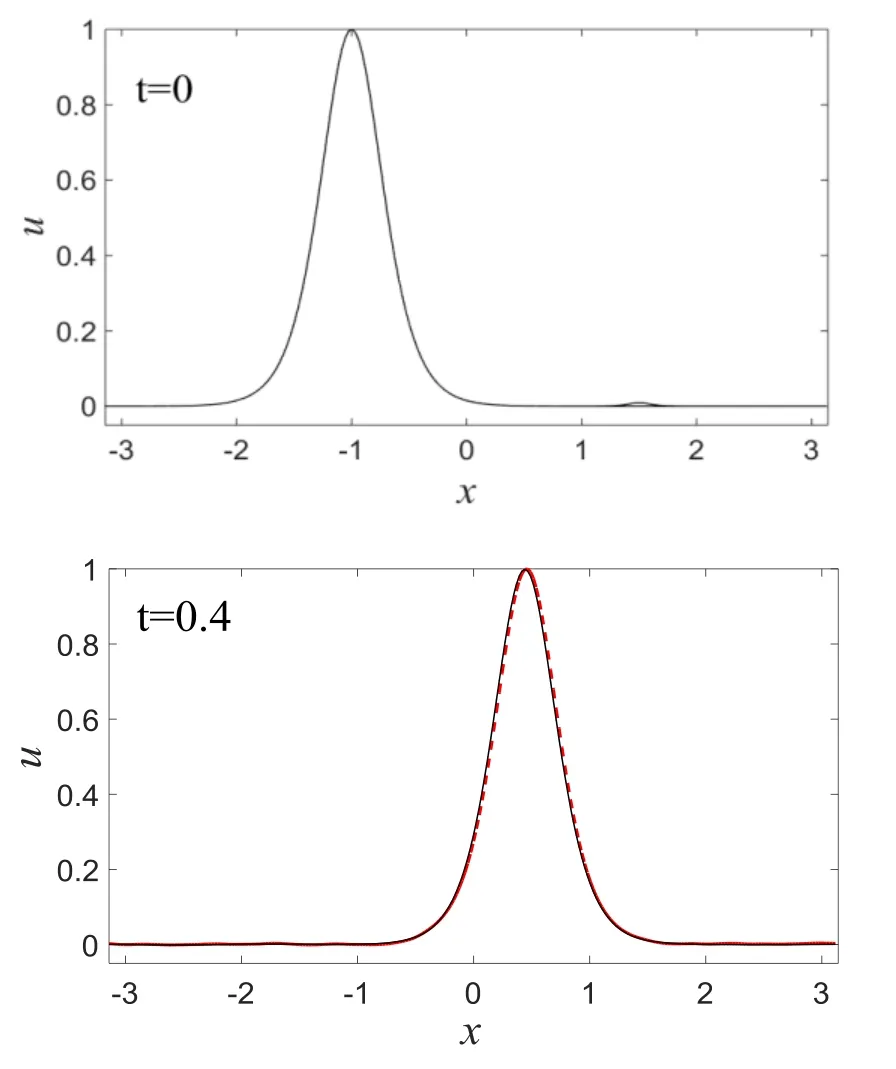
图10 双曲正割波扰动下的孤立波（红色虚线）Fig.10 The solitary wave（red dashed line）disturbed by Hyperbolic secant wave

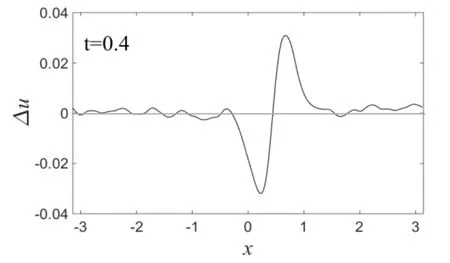
图11 受扰孤立波与未受扰孤立波的偏差Fig.11 The deviation of disturbed solitary wave and undisturbed solitary wave

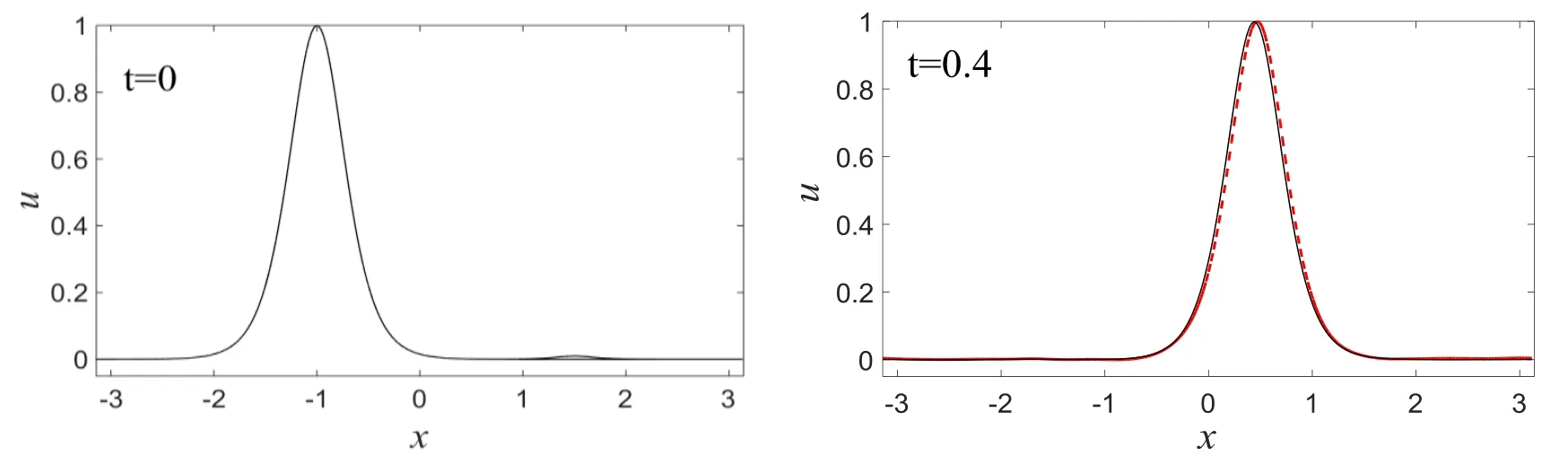
图12 双曲正割波扰动下的孤立波（红色虚线）Fig.12 The solitary wave（red dashed line）disturbed by Hyperbolic secant wave

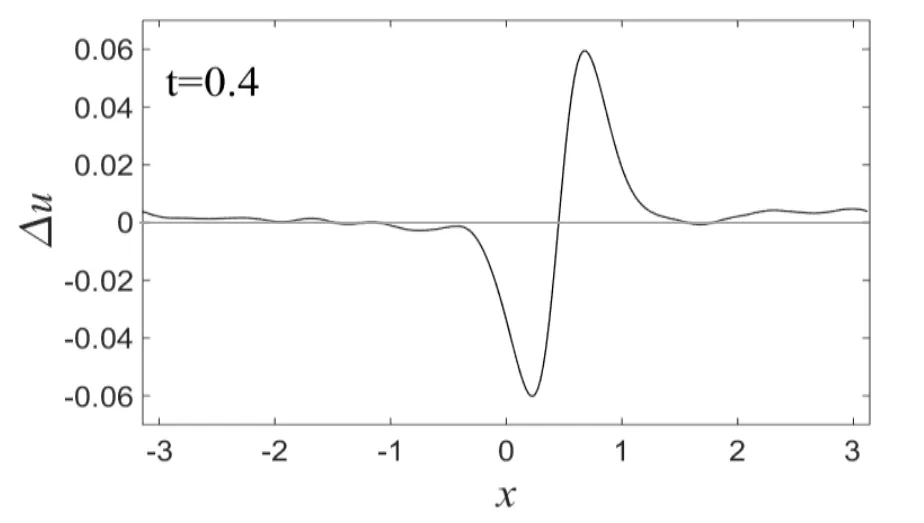
图13 受扰孤立波与未受扰孤立波的偏差Fig.13 The deviation of disturbed solitary wave and undisturbed solitary wave

3 结论

描述微结构固体中波传播的一种KdV类方程作为控制方程，并利用积分因子方法，对受到不同小扰动的孤立波在具有弱微尺度非线性效应的微结构固体中传播的动力学稳定性进行了数值模拟研究.主要结论有：

（1）在高斯波扰动、Ricker子波以及双曲正割波扰动下，孤立波的动力学稳定性都与三种扰动的幅度和宽度有关.

（2）微结构固体中传播孤立波的动力学稳定性不是很强，只有受到幅度和宽度都非常小的小扰动下，微结构固体中传播的孤立波才能显现出一定程度的动力学稳定性.

（3）扰动幅度和宽度基本相同的情况下，相比Ricker子波扰动，高斯波扰动和双曲正割波扰动对孤立波的影响更明显一些.只有稳定传播的孤立波，才能克服扰动，能够长时间传播，且能在实验中观测到和实际中可能利用到.从此意义上讲，微结构固体中孤立波能否稳定传播问题的研究对固体材料性能的无损检测与评价具有重要实际意义.希望本文结果会对微结构固体的无损检测与评价提供理论指导和帮助.