二阶多智能体系统的线性广义一致性*

柴洁 过榴晓 陈晶 陈良康

（江南大学理学院，无锡 214122）

引言

近年来，随着人工智能技术的快速发展和在实际生活中的广泛应用，多智能体系统研究吸引了越来越多各领域学者们的兴趣.而一致性作为多智能体系统协调控制中最基本的问题之一，受到许多热切的关注.

目前，大多数文献是研究多智能体网络系统的完全一致性［1.2］，即多个智能体组成的系统在控制协议的作用下，它的状态变量（如位移、速度等）逐渐趋同.一些学者从另外的角度出发，考虑智能体之间存在性能和合作任务上的差异，研究了多智能体系统的非精确一致性问题及其变种，比如文献［3-5］研究了群一致性问题，即智能体被分为多个群体，同一群体内的信息收敛到一致，不同群体间的一致状态可以不同.文献［6］提出一阶非线性领导-跟随多智能体系统的部分分量一致性的概念，文献［7］进一步讨论了二阶多智能体系统的部分状态量一致性问题.文献［8］考虑了蜂拥控制的特殊群集问题，相对群一致性还要考虑蜂拥系统中的分离和聚合两个原则.而在一些特殊的任务和环境中，个体之间还需要达到和保持预先给定的队形，同时又要适应环境约束，这是多智能体系统协调控制中的编队控制问题［9］，它与一致性有着密切的关系.

典型的多智能体系统非精确一致性为广义一致性.文献［10-13］研究了复杂网络的广义同步现象，即耦合系统的动力学之间存在某种已知或未知的函数关系.在此基础上，文献［14］提出了线性和非线性的一阶多智能体系统广义一致性的定义.由上述文献的启发，本文拟将一阶多智能体系统的广义一致性概念推广到二阶多智能体系统，理论推导二阶多智能体系统实现线性广义一致的充分必要条件，进一步，参考文献［15-20］中对通信协议的信号延时的存在对系统多智能体实现一致性控制的影响和条件的分析，给出了二阶多智能体系统最大容许时滞与固定拓扑图的Laplacian矩阵特征值之间的关系.

事实上，广义一致性是一个更自然的概念，也是作为多智能体系统输出一致性的一种特例.广义一致性能够更自然地描述由多个相互作用分量组成的生物和物理系统中的一些相干现象，具有一定的理论意义和实践价值.本文考虑二阶多智能体系统实现广义一致性问题，理论和数值实验讨论非延迟和延迟通信控制协议下的系统实现线性广义一致性的充分必要条件，通过多个仿真实例验证了结果的正确性.

1 问题描述

1.1 预备知识

1.2 模型描述

设有N个一阶智能体系统，每个智能体的动态方程为：

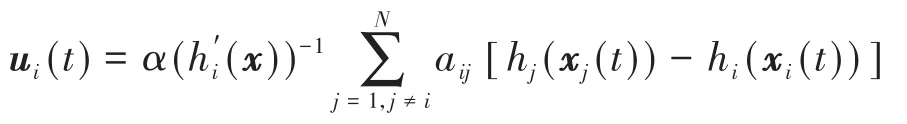
如果对于所有的i=1，2，…，N，hi（x）=x/ki，ki≠0，则称系统（1）实现线性广义一致性，如果至少存在一个hi（x）为非线性的，就称系统（1）实现了非线性广义一致性.

进一步，本文讨论N个智能体的二阶多智能体系统，各智能体的动态方程为：

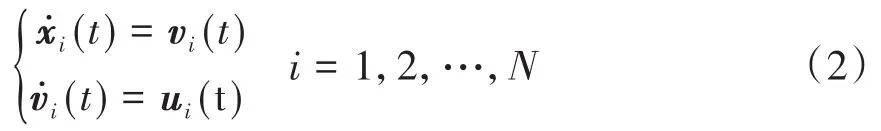
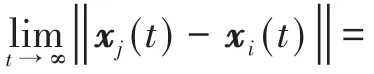
现在把文献［14］中一阶多智能体系统的广义一致性定义推广到了二阶情形.

定义1 对于任意初始条件xi（0）∈R，vi（0）∈R，i，j=1，2，…，N，如果满足

则称二阶多智能体系统（2）实现广义一致性.

简单起见，本文只研究线性的广义一致性问题.

定义2 对于任意初始条件xi（0）∈R，vi（0）∈R，i，j=1，2...N，如果满足

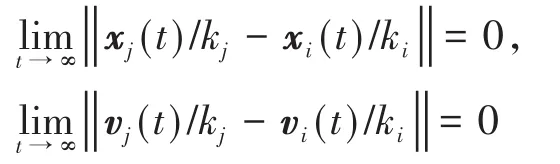
则二阶多智能体系统（2）关于参数ki，i=1，2，…，N实现线性的广义一致性.

注1 当参数ki，i=1，2，…，N为若干组不同但组内相同的参数，则二阶系统可实现分组一致状态.更特殊的，当参数ki，i=1，2，…，N有两组，分别为1和-1，即二阶系统达到竞争与合作［15］的反分组状态.所以，本文提出的二阶多智能体系统线性广义一致概念可视为更一般的情形.

设计控制协议如下：

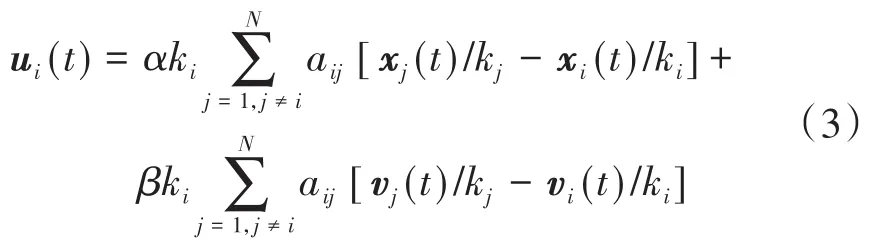
其中，ki，i=1，2，…，N.为N个非零常数.α，β表示耦合参数.由式（2），式（3）和拉普拉斯矩阵的定义，系统等价表示为：

2 主要结果

2.1 无通信延迟情形

本节将研究系统（5）关于参数ki的线性广义一致性的实现与耦合参数α，β及拉普拉斯矩阵L的特征值之间的关系.令uij（i=1，2，…，N；j=1，2），分别表示矩阵和拉普拉斯矩阵L的特征值.

引理1［21］拉普拉斯矩阵L有一个0的特征值，并且其它特征值均有正实部，当且仅当有向图G包含一个有向生成树.

引理2［22］二阶多智能体（5）能够实现线性广义一致性，当且仅当矩阵含有一个特征值0（二重），并且其它特征值含有负实部.此外，如果二阶线性广义一致性实现，则当t→∞时有：

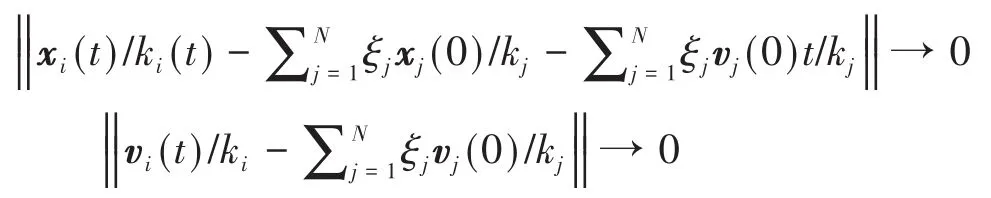
这里ξ是拉普拉斯矩阵L关于特征值0的唯一非负左特征向量，满足ξT1N=0.

定理1 二阶多智能体系统（5）实现线性广义一致性，当且仅当：

1）有向图G包含一个有向生成树；

3）K为可逆矩阵，即ki≠ 0，i=1，2，…，N.（6）证明 作矩阵的特征多项式：

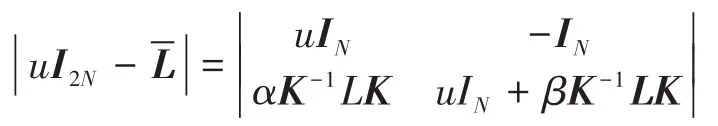
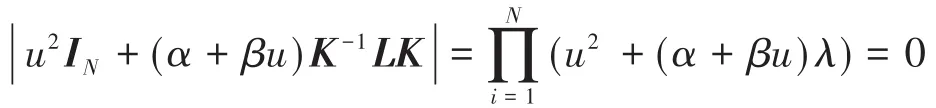
这里λi（i=1，2，…，N）表示拉普拉斯矩阵L的特征值.

由此可知：矩阵L有一个代数重数为m的0特征值，当且仅当矩阵有一个代数重数为2m的0特征值.由引理1和引理2，只需要证明：Re（λi）>0，（i=2，3，…，N），且条件2）成立，当且仅当Re（uij）<0，（i=2，3，…，N；j=1，2）.

消除d可得到

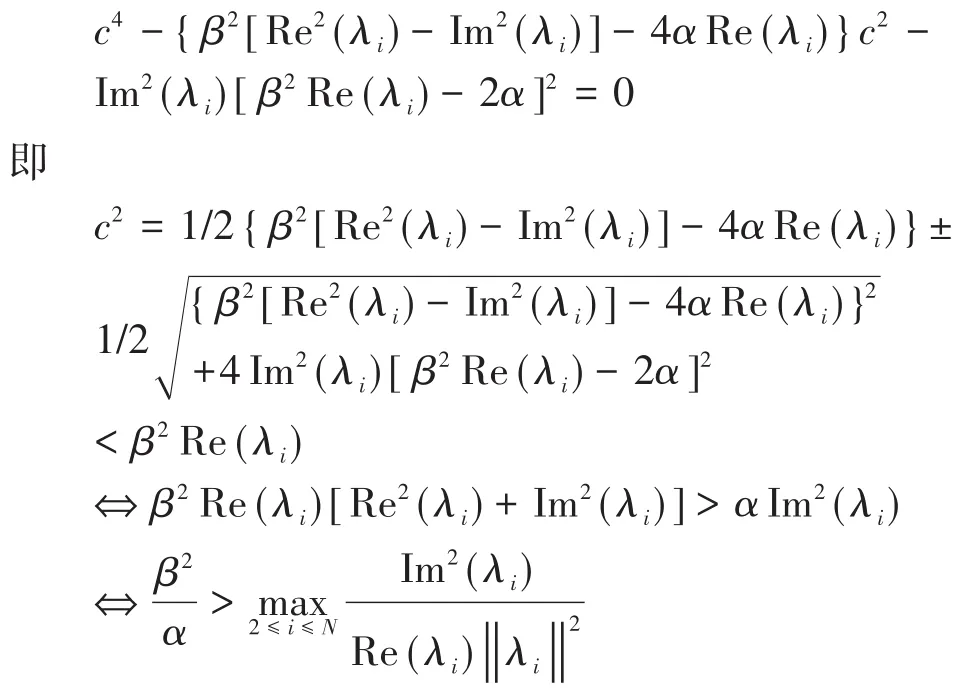
证毕.

注2 由定理1知，耦合参数α，β及拉普拉斯矩阵L的特征值对系统一致性的实现起着十分重要的作用，且若hi（x）是线性函数，即hi（x）=x/ki，ki≠0，则理论上系统线性广义一致性的实现与ki的取值无关.

2.2 有通信延迟情形

在系统（2）中，假设设计控制协议中带有通信延时：

这里，τ>0为时间延迟常数.令

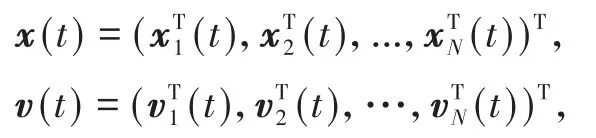
则系统（2）和（8）的等价矩阵形式为：

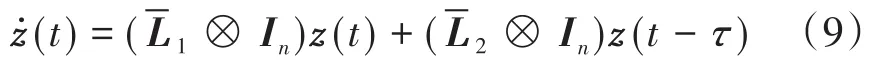
这里，

计算系统（9）的特征方程为

由系统（9）的特征方程很容易得出：L有一个代数重数为m的0特征值.当且仅当g（u）=0有一个2m重零根.给出以下3个引理：

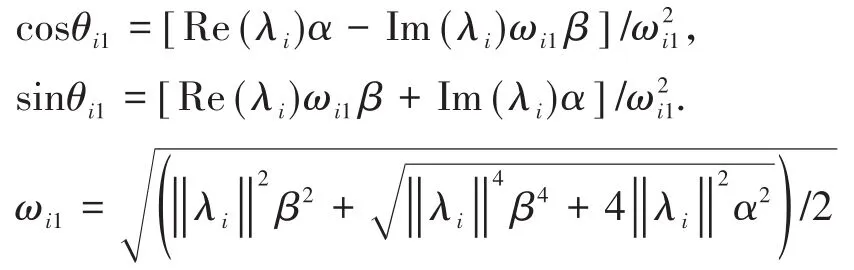
引理4［23］对于指数多项式

引理5［22］假设有向图G包含一个有向生成树.u是gi（u）=0，2≤i≤N的解，那么当τ∈ψ时，du/dτ存在，并且Re（du/dτ）|τ∈ψ>0.

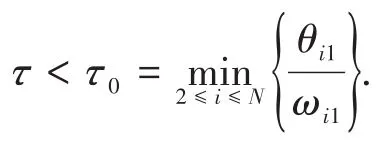
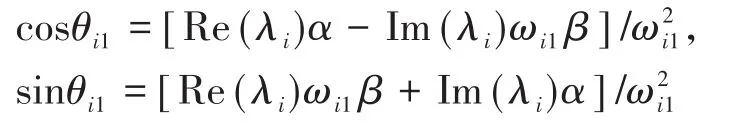
其中，

证明 因为有向图G包含一个有向生成树，并且满足定理1中的2）、3）式，故由定理1知，当τ=0时，系统（9）能够实现线性广义一致性.再由引理2知g（u）=0含有一个零根（二重），并且其它根含有负实部.当τ从0变化到τ0时，由引理3知一个纯虚根会出现.由引理4和引理5知，当0≤τ<τ0时，g（u）=0有一个零根（二重），且其它根含有负实部，系统（9）实现线性广义一致性，而当τ>τ0时，至少存在一个具有正实部的根，故当τ>τ0时无法实现一致性.证毕.

注3 定理2在定理1的基础上给出了延迟通信的二阶多智能体系统满足线性广义一致性的充要条件，即延迟参数τ要小于一个临界值，且给出了这个最小临界值τ0的具体求法.由于τ0的求解与拉普拉斯矩阵L特征值的实部与虚部有关，实际特征值的精度对τ0的计算影响很大，所以，实际操作中，可以适当提高计算精度，减少误差带来的影响.

3 数值仿真

3.1 系统无时延情形

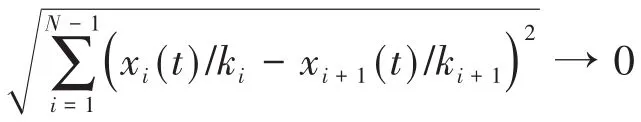
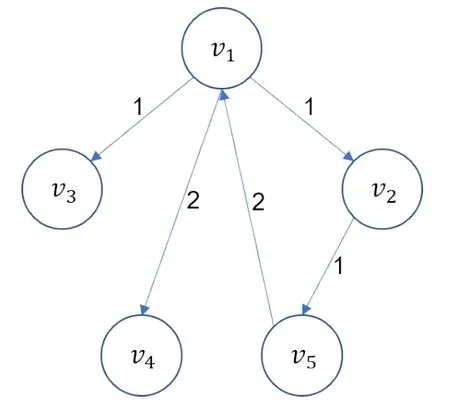
图1 有向加权图GFig.1 Directed weighted graphG

图2 当α=0.1，β=0.15时系统位置和速度状态轨迹图Fig.2 Position and velocity state trajectory of the system with α=0.1，β=0.15

图3 当α=0.1，β=0.15时系统全局误差演化图Fig.3 Evolution of the system global error withα=0.1，β=0.15

图4 当α=0.1，β=0.05时系统全局误差演化图Fig.4 The Evolution of the system global error with α=0.1，β=0.05

3.2 系统有时延情形

系统（9）中取参数 N=5，n=1，α=0.1，β=0.5，非零线性广义参数和连接拓扑图同上.由定理2计算可得控制协议中最大时间延迟τ0=0.822.当τ=0.7时，多智能体在各自参数下的投影状态轨迹如图5所示，系统（9）能够实现关于参数的线性广义一致性.而当τ=0.9不满足定理2的充要条件，此时由图6可知系统（9）不能达到线性广义一致性.

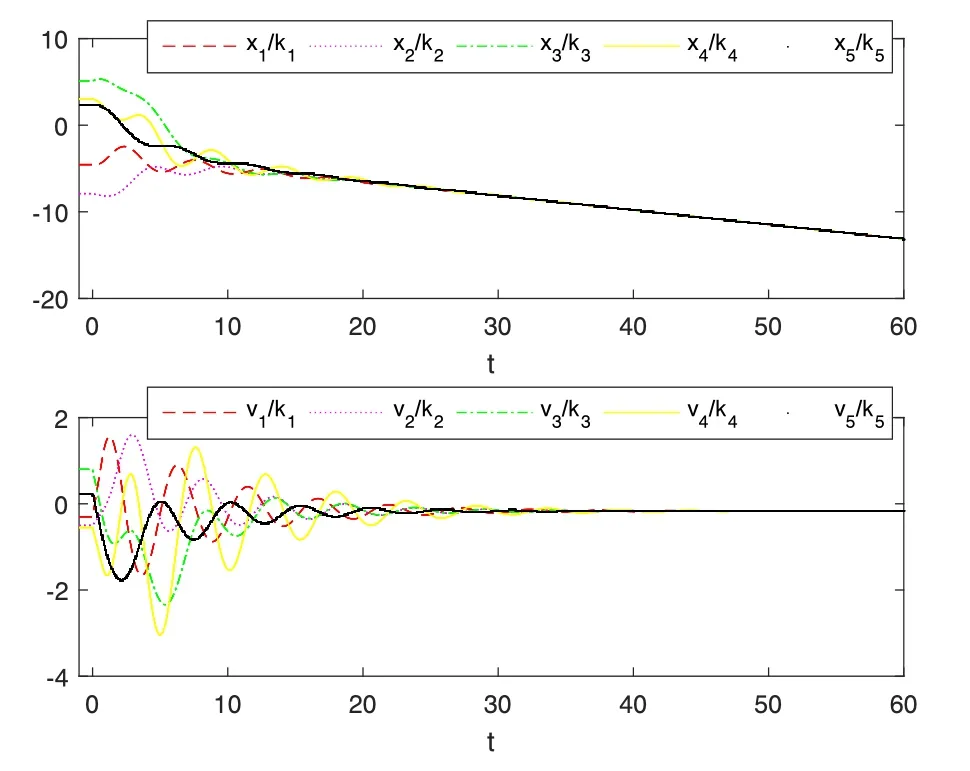
图5 当α=0.1，β=0.5，τ=0.7时系统位置和速度状态轨迹图Fig.5 The position and velocity state trajectory of the system withα=0.1，β=0.5，τ=0.7

图6 当α=0.1，β=0.5，τ=0.9时系统位置和速度状态轨迹图Fig.6 The position and velocity state trajectory of the system with α=0.1，β=0.5，τ=0.9

4 小结

本文研究了二阶多智能体系统关于多参数的线性广义一致性，在有向网络拓扑结构下设计了有效的控制协议，获得了系统在有时延和无时延两种情况下实现线性广义一致性的充分必要条件，并运用代数图论和稳定性等理论给出了证明.在接下来的工作中作者将讨论二阶多智能体系统的非线性广义一致性以及广义群一致性等问题.