分布式阵列在定向通信DOA 估计中的应用*

高龙超

（中国西南电子技术研究所，四川 成都 610036）

0 引言

定向天线相比全向天线具有增益高、抗干扰以及低截获的特性，因此在通信系统中的应用越来越广泛。使用定向天线进行通信的系统称为定向通信系统。定向通信吸引了众多学者的研究。文献[1]研究了定向通信的MAC 协议。文献[2]提出了一种基于时分调度的定向通信信息共享方法。定向通信系统除了具备高增益带来的通信距离远的优点外，还可利用定向天线的方向性进行角度测量。通信系统可使用角度测量信息实现相对导航[3]。角度精度越高，相对导航精度越高。因此，获取高精度的DOA 估计对定向通信系统十分重要。DOA 估计精度与天线孔径密切相关，天线孔径越大，精度越高。使用阵列天线是扩大天线孔径的普遍做法，而过多的增加阵元数目会使天线硬件成本过高，且算法计算量急速增加。文献[4]提出使用分布式阵列扩充阵列孔径获取高精度测角结果，先通过子阵获取无模糊的角度估计，再通过分布式合成阵列获取高精度有模糊的角度估计，将二者结合最终得到无模糊高精度的角度估计。已有的使用分布式阵列进行DOA 估计的文献均是基于文献[4]的思想，需要两次使用空间谱估计算法。两次空间谱估计算法对应两次矩阵特征值分解，算法运算量较大。这些文献均以雷达为研究背景，本文研究的对象是定向通信，而通信与雷达的一个显著区别为通信双方是合作方。通信双方建立通信后可进行信息交互，如位置信息[5]。通信系统利用双方的位置信息可以得到通信对象的角度估计，这一计算过程相比空间谱估计算法运算量小得多，可以用该角度估计解分布式合成阵列的角度模糊。本文将分布式阵列应用于定向通信系统的角度估计，利用通信系统的合作特性，根据通信双方的位置信息得到精度较低的角度估计结果，再使用一次空间谱估计算法得到无模糊的高精度角度估计结果。整个DOA 估计过程只需一次矩阵特征值分解。

1 信号模型

分布式阵列的布阵方式如图1 所示，由两个子阵构成，且两个子阵相同。子阵是阵元数为M的均匀线阵，且两个子阵在同一条直线上。阵元间距d=0.5λ，λ为通信信号的波长。两个子阵的间距为R。

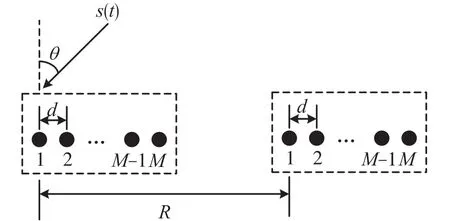
图1 分布式阵列布阵示意

假设某一时刻使用该分布式阵列的定向通信系统在通信过程中只有一个通信对象。若分布式阵列覆盖范围内有多个通信对象，则分时通信，因此某一时刻只有一个通信对象的信号到达该分布式阵列。本文使用空间谱估计算法获取有测角模糊的高精度DOA估计，需要先建立分布式阵列的信号模型。假设有一个窄带远场信号到达该阵列，到达角为θ，以图1 中左边子阵的阵元1 为参考，则该阵列的数据接收矢量X(t)为：

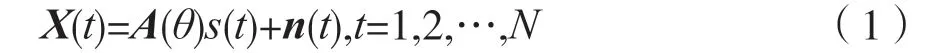
式中：s(t)为信号复包络；n(t)为噪声，其均值为0，长度为2M；N为快拍数，即一个通信时隙内接收N个脉冲信号。

A(θ)为该阵列的导向矢量：

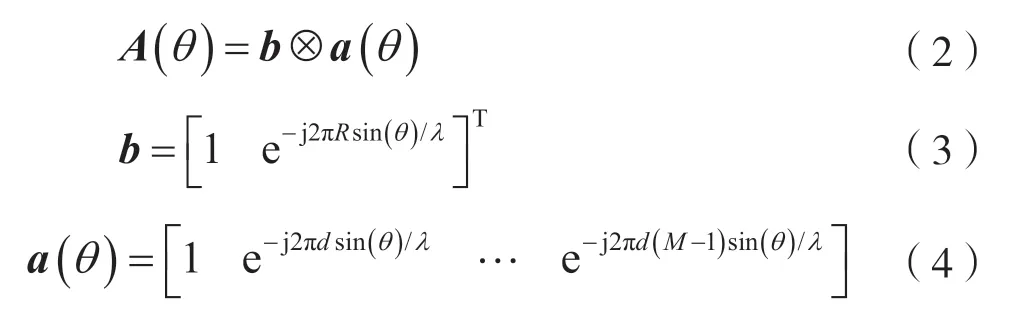
根据一个通信时隙内N个脉冲信号的数据接收矢量得到阵列协方差矩阵：

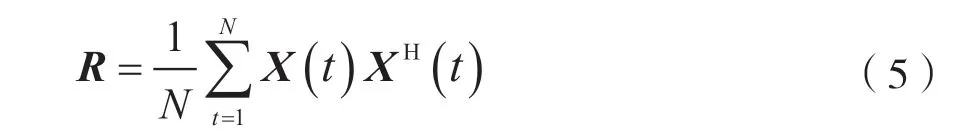
对其进行特征值分解：

式中，U1为最大特征值对应的特征矢量形成的信号子空间，U2为其他特征值对应的特征矢量形成的噪声子空间，T1为最特征值，T2为其他特征值形成的对角矩阵。

2 DOA 估计方法

为了扩大阵列孔径，如图1 所示的分布式阵列中两个子阵拉开的间距一般较大。根据相控阵天线工作原理可知，该阵列的天线方向图会出现栅瓣。使用经典的谱MUSIC 算法[6]在作用空域进行谱峰搜索，必然有测角模糊。为了解模糊，首先需要获取一个无模糊的测角结果，由该测角结果确定一个搜索范围，使得在该范围内不包含MUSIC 空间谱的伪峰但包含实际峰值，以得到无模糊的高精度测角结果。通信系统可通过通信双方的位置信息得到通信对象的DOA 低精度角度估计。通信系统所在平台的惯性导航系统可将本平台位置信息送给该通信系统，而通信对象的位置信息可通过无线通信链路传输过来[5]即平台定位信息共享，这是战术数据链的基本功能。

2.1 低精度角度估计

惯性导航系统以经度、纬度、高度的形式给出位置信息，相应的坐标系称为经纬高坐标系。经纬高坐标系是大地坐标系的一种，但其不是直角坐标系。使用经纬高计算通信对象的角度时，需要先进行坐标系转换，将经纬高坐标系下的坐标值转换为地理直角坐标系下的坐标值。

对于本文研究的定向通信系统，先假设其阵列布阵与地理直角坐标系的X轴在同一条直线上。如图2 所示，P1为本通信系统所在平台，P2为通信对象所在平台。

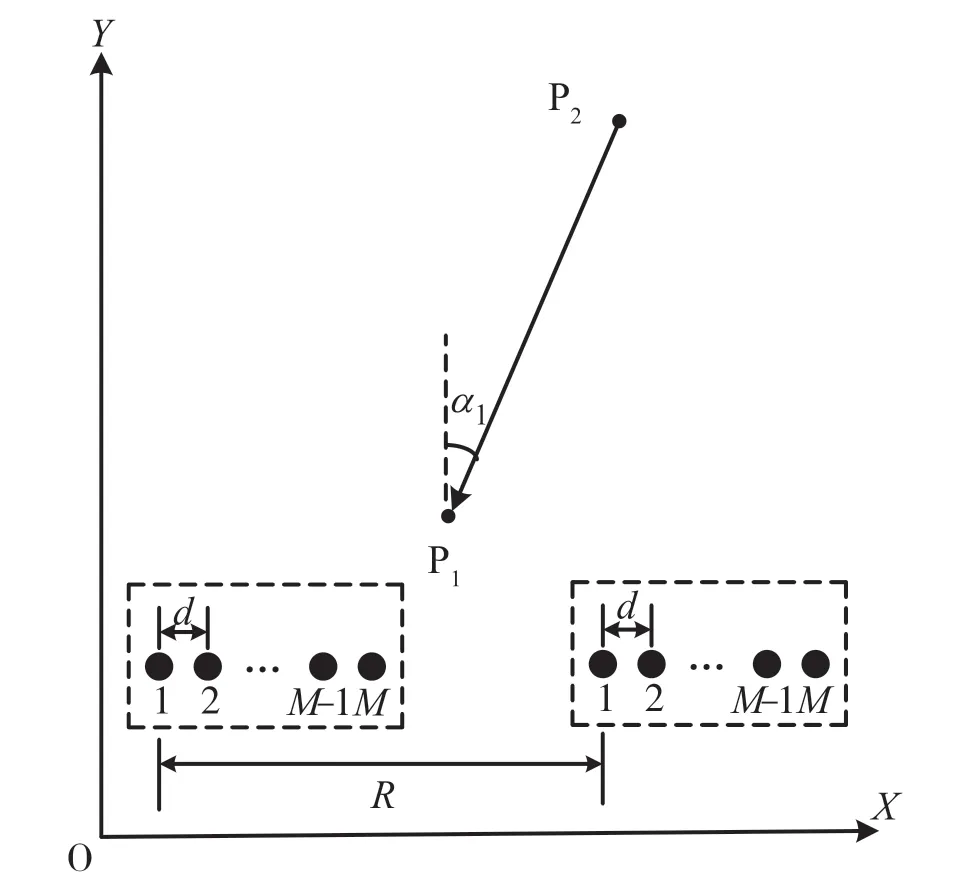
图2 通信双方位置关系示意

通信双方经纬高坐标系下的坐标可通过惯性导航系统获取。根据文献[7]，将通信双方的坐标值从经纬高坐标系转换到地理直角坐标系。地理直角坐标系下，根据P1(x1,y1)、P2(x2,y2)的位置，可计算出相对于P1的方位角：

前文假设如图2 所示的阵列与地理直角坐标系的X轴在同一条直线上，但实际上并非如此。根据式（7）计算得到α1后，还需将地理直角坐标系先转换到平台坐标系，再转换到天线坐标系，得到天线坐标系下的角度，才可以用来解模糊：

式中，u表示平台姿态角矢量，w表示天线安装角矢量，v为坐标系转换函数。根据文献[8]介绍的转换方法，地理坐标系转换到平台坐标系，转换矩阵由平台姿态角决定；平台坐标系转换到天线坐标系，转换矩阵由天线安装角决定。本文不再详细描述坐标系转换方法。平台姿态角由惯性导航系统给出，天线安装角由激光雷达测量得到。这两组测量数据存在一定误差，为随机误差。随机误差大小分别由惯性导航系统和激光雷达的测量精度决定。

2.2 确定无模糊搜索范围

根据式（7）和式（8）得到无模糊角度估计，并需要根据这一无模糊的角度估计确定谱MUSIC算法的搜索范围，使其在该范围内无角度模糊，从而得到无模糊的高精度角度估计。根据文献[9]，图1 的分布式阵列MUSIC 空间谱伪峰出现的位置与入射信号方向的方向图的栅瓣位置一一对应，即可由栅瓣位置确定MUSIC 谱的伪峰位置。根据文献[9]，MUSIC 谱实际峰值与两侧第一伪峰的距离为2arcsin(0.5λ/R)。只要使得算法搜索范围内MUSIC谱不出现伪峰，就能实现解模糊。

谱MUSIC 算法无模糊搜索范围为：

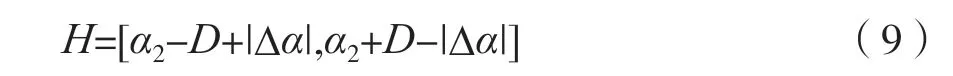
式（9）考虑了α2误差的影响，其中α2如式（8）所示。∆α为其误差，D=2arcsin(0.5λ/R)。若α2的误差为0，则谱MUSIC 算法的搜索范围为H1=[α2-D,α2+D]。H可以看作是对H1的修正。由于α2误差的存在，需要将区间H1缩小，避免区间内包含MUSCI 空间谱的伪峰。由区间的定义可知，只有当∆α满足式|∆α|＜2arcsin(0.5λ/R)，H才有意义，否则H下确界大于上确界。

2.3 无模糊高精度角度估计

使用谱MUSIC 算法进行空间谱搜索，式（9）作为搜索区间，则无模糊高精度角度估计结果为：

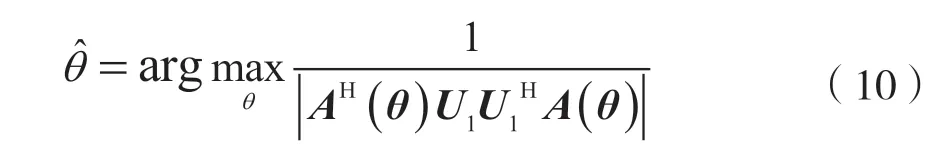
式中，H如式（9）所示；A(θ)为分布式阵列的导向矢量，如式（2）所示；U1如式（6）所示，为最大特征值对应的特征矢量形成的信号子空间。由式（9）可知，H的长度为l=4arcsin(0.5λ/R)-2|∆α|。若搜索步进为k，则谱MUSIC 算法的搜索次数为l/k。

2.4 运算量分析

由本文方法的流程可知，本文方法高精度角度估计涉及一次矩阵特征值分解。低精度角度估计只涉及坐标转换，不涉及矩阵特征值分解，而文献[9]的方法两次角度估计各需一次矩阵特征值分解。本文方法低精度角度估计运算量与阵列规模无关，即运算复杂度为O(1)。文献[9]的低精度角度估计的运算量为O(6M+2MN+M3)，而高精度估计运算量本文方法与文献[9]方法相当。因此，本文方法总的运算量小于文献[9]。本文方法低精度角度估计运算量小的原因在于利用了定向通信系统的合作性。

3 计算机仿真

假设图1 中定向通信系统的子阵阵元数为10，子阵间距R为15λ（λ为通信信号的波长），信号入射方向为30°。平台姿态角误差、天线安装角误差引起的无模糊测角误差为1.5°，根据定向通信系统双方位置和姿态角计算得到的角度估计为31.1°，则使用谱MUSIC 算法时的搜索区间为[28.8，33.4]。图3 给出了信噪比为0 dB 时的MUSIC 空间谱，可知该区间不包含伪峰，可以成功解模糊。

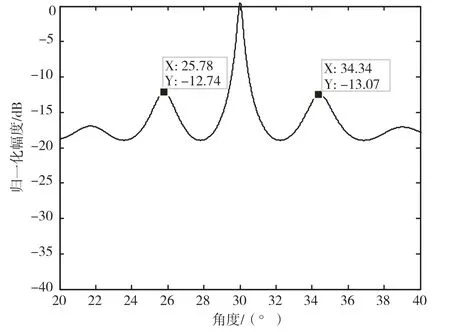
图3 分布式阵列MUSIC 谱

图4 给出G=2arcsin(0.5λ/R)随子阵间距R的变化情况。当低精度角度估计误差|∆α|＜G时，可以成功解模糊；当|∆α|≥G时，解模糊失败。可见，对于该通信系统，当R＜38λ时，可以成功解模糊；当R≥38λ时，解模糊失败。

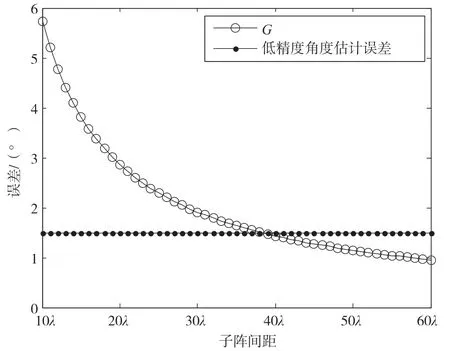
图4 解模糊条件随子阵间距的变化

图5 给出DOA 估计精度随信噪比变化的仿真结果。可见，在低信噪比下能得到高精度DOA 估计结果。

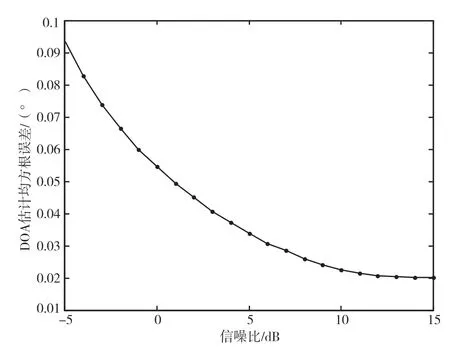
图5 DOA 估计精度随信噪比的变化

4 结语

提出使用分布式阵列的布阵方式扩大定向通信系统的阵列孔径，利用通信双方的位置信息计算无模糊的角度估计，并由该角度估计确定谱MUSIC算法的搜索区间。在该区间内不包含MUSIC 谱的伪峰，能够实现解模糊。所提方法的低精度角度估计运算量与阵元规模无关，运算量较小。计算机仿真结果验证了所提方法的有效性，可为定向通信系统分布式阵列的布阵提供工程指导。