基于Xampling 的MWC 系统设计与实现*

张飞正，张 亘，邱海舰

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

随着信号处理技术的发展，信号处理正在由模拟领域向数字领域转变。现代雷达、通信等信号处理系统通常要求先对天线接收到的信号进行数字化处理，根据传统的采样理论，对这些信号进行无失真恢复所需要的奈奎斯特采样率可能会超过目前商用模拟数字转换器（Analog-to-Digital Converter，ADC）好几个数量级，给硬件设计带来了极大困难。因此必须通过进一步研究信号的结构，以求获得更多的信息，实现信号的恢复。而实际应用中的无线电信号在传输过程中，都会被调制到很高的载频上，也就是说相对于整个频谱，它只包含了很少的窄带信号，这种信号称为稀疏多频带信号。

当信号载频已知时，Landau 和Lin 分别用不同的方式提出所需要的最小采样率为各频带带宽之和[1]，当信号载频未知时，一个挑战性的任务是如何以远低于奈奎斯特采样率实现信号的盲恢复。多陪集采样理论体系提出了全盲信号恢复系统[2]，但由于对时延的准确度要求很高，实际中难以实现。基于压缩感知理论提出的随机调制器可以恢复出多频信号[3]，但由于模拟信号需要大量的谐波才能近似逼近，而如此多的谐波极大地增加了重构的复杂度。而基于Xampling 信号恢复算法利用调制宽带转换（Modulated Wideband Converter，MWC）系统，既能对稀疏多频带模拟信号以远低于奈奎斯特采样率进行采样，又为硬件提供了易实现可能。本文正是基于Xampling 信号恢复算法理论，对信号进行降采样恢复而设计的一套低速率采样盲恢复硬件MWC 系统。

1 MWC 系统原理

1.1 稀疏多频带信号模型

在通信领域，现在的通信信号一般是由几个具有一定带宽的信号组成，分布在很宽的频带范围之内。且相对于奈奎斯特采样率fNYQ，带宽一般都很窄。其频谱示意图如图1 所示：

图1 典型通信信号频谱

针对具有这种特征的稀疏多频带模拟信号，可采用MWC 模型来降低信号的采样频率。本文针对具有6 个子带的稀疏多频带模拟信号作为信号模型来分析。

1.2 MWC 系统简介及Xampling 原理

假设一个连续时间实信号x(t)，它的频谱位于[-1/2T,1/2T]之间，其中1/T=fNYQ，fNYQ为奈奎斯特采样率。一般情况下，信号x(t)在频域上是分段连续的。在图1 所示的信号模型中，信号在频谱中只有6 段频谱，定义参数N=6。

MWC 系统框图如图2 所示，包括乘法器、低通滤波和采样3 个过程。

图2 MWC 系统

从图2 中可以看出，模拟信号x(t)同时进入m个信道。在每个信道中，信号x(t)首先与随机序列pi(t)相乘。在理论上，pi(t)只需要是一个周期信号即可，即：

信号x(t)与pi(t)相乘之后，经过一个截止频率为1/2Ts的低通滤波器，然后被采样率为1/Ts的ADC 采样。

接下来分析MWC 采样系统的原理，任意取一个信道i进行分析，因为信号pi(t)是周期函数，所以有：

式中，有：

信号x(t)与pi(t)相乘之后，定义：

式中，X(f)为原始信号x(t)的频谱，为信号的频谱。

从上述分析可以看出，信号x(t)与pi(t)相乘之后，即是对x(t)频谱的搬移。所以，滤波器的输入是原始信号频谱X(f)经过lfp搬移之后的线性组合。假设原始信号x(t)频谱中每一段频谱宽度均不超过B，即B为每一段频谱的最大带宽。因信号的频谱分布位于[-fNYQ/2,fNYQ/2]范围之内，所以任意一路信号频域最多有|fNYQ/B|个非零部分。信号经过低通滤波器之后，只有位于[-fs/2,fs/2]之间的频谱被保留了下来。因此，经采样后，信号yi[n]的离散傅里叶变换为：

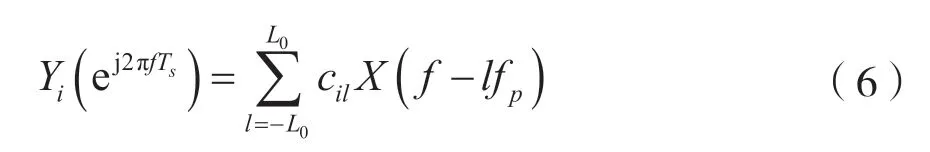
式（6）建立了采样之后的信号yi[n]的频谱与未知原始信号x(t)的频谱之间的关联，是后面的恢复算法的关键。为了方便后面的分析，将式（6）写成矩阵的形式，如下：

式中：

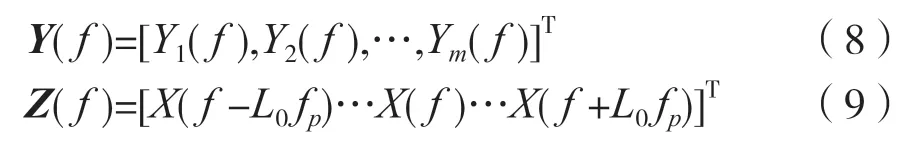
在矩阵A中，有：

定义：

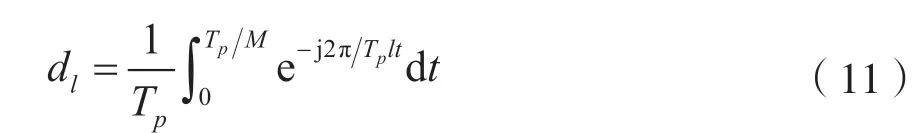
计算可得：

同时，还定义θ=e-j2π/M，所以化简可得：

定义：

令S为m×M的符号矩阵，即Si,k=αi,k，D=diag(dL0,…,d-L0)，其中dl由式（11）得到，于是有：

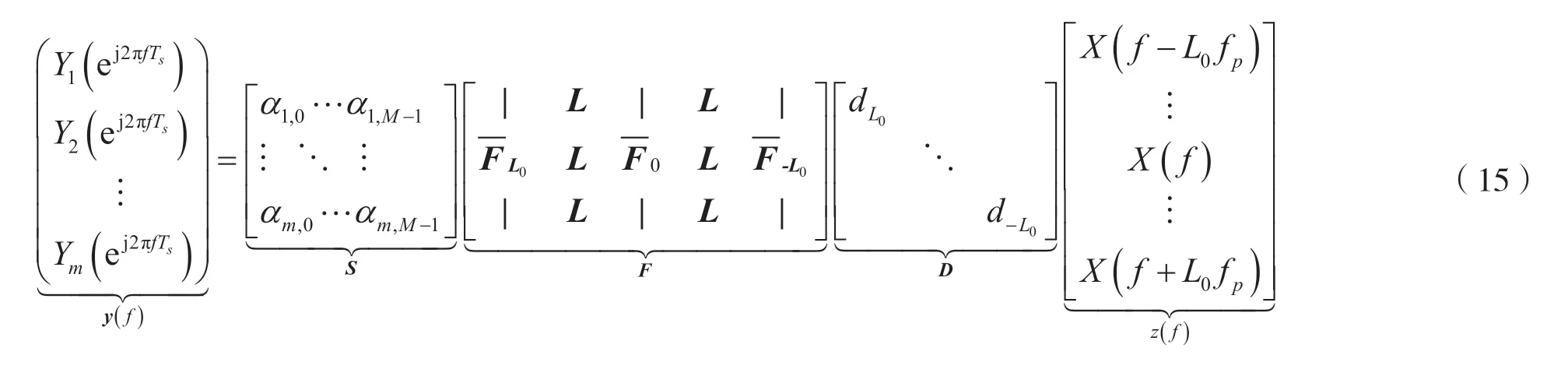
至此，MWC 模型的基本过程已经分析完毕。从中可以看出，原始信号经过与伪随机序列相乘，低通滤波，采样之后，原始信息的频域与采样之后的信号频谱之间建立了关联，这也是Xampling 恢复算法的理论基础和依据。而恢复算法的本质就是去求解这样一个未知数个数多于方程个数的矩阵的方程。

1.3 Xampling 恢复算法

以上讲述了MWC 模型中的采样部分，下面开始介绍如何从采样得到的信息中恢复出原始信号。恢复原始数据Z的本质是求解未知数个数多于方程个数的方程。然而，因为未知数中大多数是0，所以只要找到待求解的矩阵中哪些位置数据为0，哪些不为0，这个方程便可以求解[4]。

首先定义，若一个向量u中只有K个非零元素，或者只有K个较大的元素，那么向量u被称为K稀疏向量。定义s=suup(u)记录的是非零元素或者较大元素在向量u中的位置。针对式（15），s中保存的是矩阵Z中非零行的位置信息。求解向量s的过程如图3 所示。

图3 s 求解

在图3 中，矩阵Y为采样得到的数据矩阵，利用公式Q=∑y[n]yT，则有：

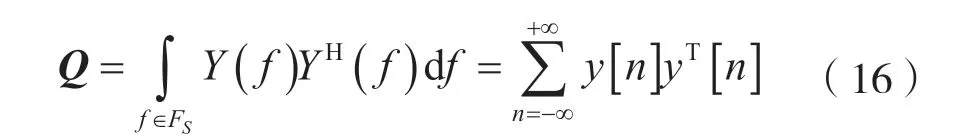
在得知矩阵Q之后，需要构造任意一个满足Q=VVH的矩阵V。此处，可以选取矩阵Q的特征向量组成的矩阵和对应特征根的算术平方根所组成的对角矩阵的乘积作为矩阵V。

在确定了矩阵V之后，便可以利用正交匹配追踪算法[5-6]来求解方程V=Cu。这样，向量s便可以确定，从而确定矩阵Z中非零元素所在的行。

定义CS为在s索引下由矩阵C中的列向量组成的矩阵。同时，定义：

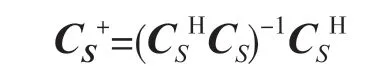
这样，便可以用公式：

去恢复信号。需要注意的是，此时，z[n]的采样率是fs。因此，还需要对此信号进行内插。内插过程用如下公式表示：

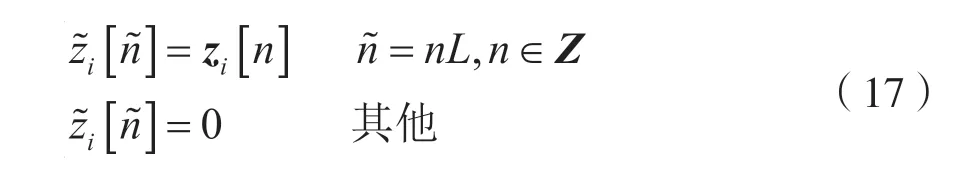
经过内插之后，信号被恢复到奈奎斯特速率。因位于不同频带的信号在采样前均被搬移到了基带，所以最后还应该把他们搬移到原来的位置。各信号经过搬移并相加之后，原始的信息便恢复了出来。

2 硬件设计部分

MWC 系统的硬件设计主要包括3 部分：现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）随机序列产生部分、混频滤波部分、数据采集传输部分。模拟部分包括功分器、乘法器、滤波器。模数转换部分主要有AD 采样，RAM 存储和采样数据串行传输。

硬件设计整体系统框图，如图4 所示。

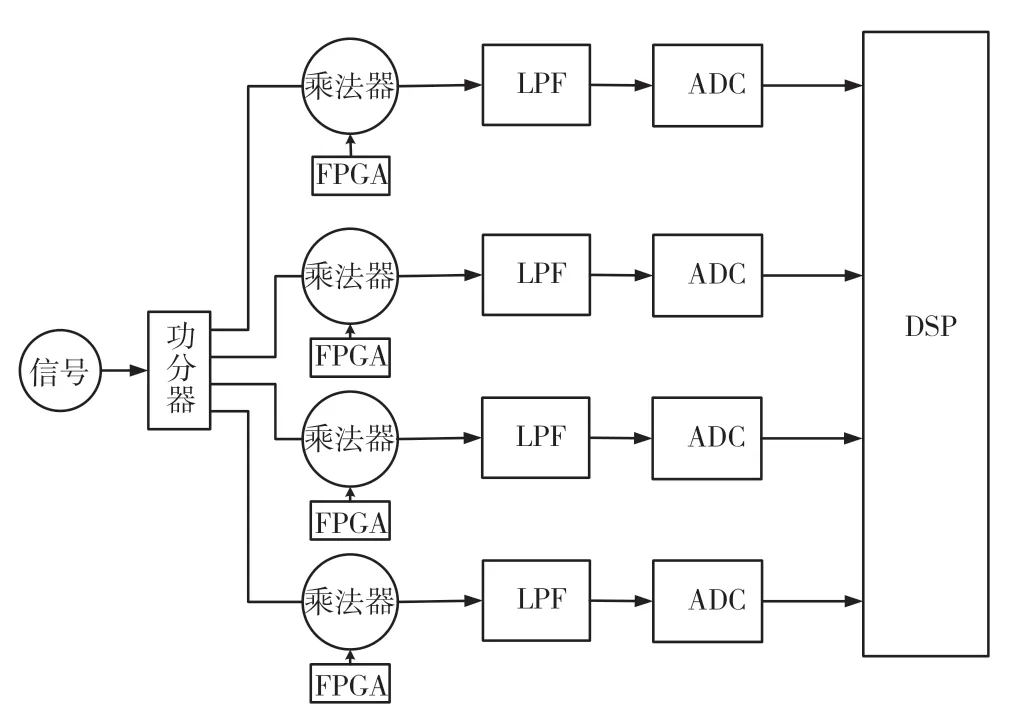
图4 MWC 系统硬件设计结构

2.1 FPGA 伪随机序列的产生

MWC系统中的随机序列必须满足一定的条件。在实际实现中，根据奈奎斯特采样率和ADC 采样率的要求，本文设计的m序列码长为403。m序列的本原多项式F(x)为F(x)=1+x4+x9。因为当n=9 时，生成的随机序列码长为m=29-1=511，大于所需要的码长403，故需要从511 个码元中从起跳状态开始跳过108 个，而且又要符合移位寄存器的输出方式。由于本原多项式为F(x)=1+x4+x9，可以推得反馈系数C0=1、C4=1、C9=1，其余反馈系数为零。故反馈函数为：图5 为m序列码长为511 时发生器逻辑图。

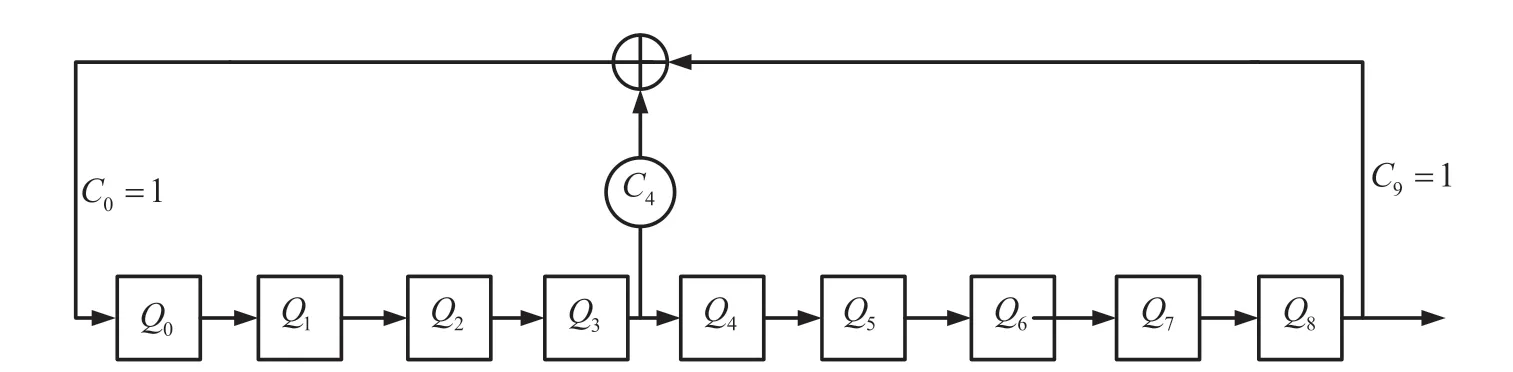
图5 m 序列发生器

在时钟CP 的驱动下，当寄存器的初始状态Q8……Q0=111111111 时，根据式，可得到m序列的输出如序列Ⅰ。为了找到起跳状态，首先将Q8的输出作为序列Ⅰ：

1 1 1 1 1 1 1 … 1 0 0 1 1 1 0 1 1 0 0 1 0 1 1 … 1 0 0 0 0 0

再将序列Ⅰ向左移108 个码元，得到序列Ⅱ：

1 0 0 1 1 1 1 … 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 … 1 0 1 1 1 0

然后将序列Ⅰ和序列Ⅱ的对应位进行模2 加运算得到序列Ⅲ：

0 1 1 0 0 0 0 … 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 … 0 0 1 1 1 0

最后，在序列Ⅲ中找到100000000，其所在的位置相对应的序列Ⅰ的码元111011001 就是要找的起跳状态。

在长度为511 的序列Ⅰ中，从起跳状态开始，消去108 个码元，剩下的码元即组成长度为403 的序列：

1 1 1 1 0 0 1 1 1 1 0 …… 0 0 1 1 1 0 1 1 0 0 1 1

所以，m=403 的序列信号发生器的反馈函数f´为：

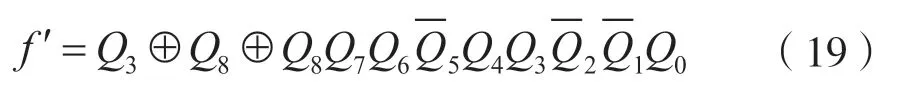
但是在最长线性序列信号发生器中，全0 状态是最长线性序列状态转移中的偏离状态。当各级触发器状态全为零时，由于反馈网络是异或网络，导致寄存器的输出一直为0，即最长线性序列信号发生器在全0 状态不具有自启动特性。为了避免寄存器状态一直为零，使其具有自启动特性，必须对反馈函数f´进行修改。修改后的激励方程为：

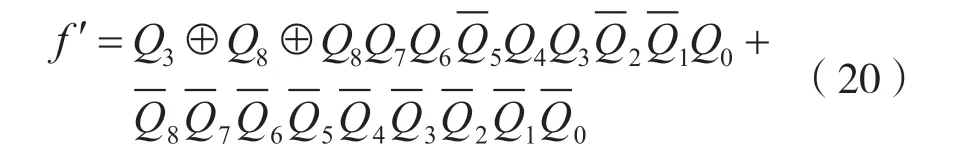
化简可得：

根据以上表达式，编写FPGA 代码。在QuartusII开发环境中，进行时钟分频设计和逻辑时序代码的编写，可以得到如图6 所示的随机序列。

为了准确的分析随机序列的频谱特性，将FPGA产生的m序列，导入到MATLAB 进行FFT 分析得到如图7 所示的随机序列频谱。可以明显看出，随机序列的频谱间隔是固定，由此也验证了所产生的m序列的正确性。

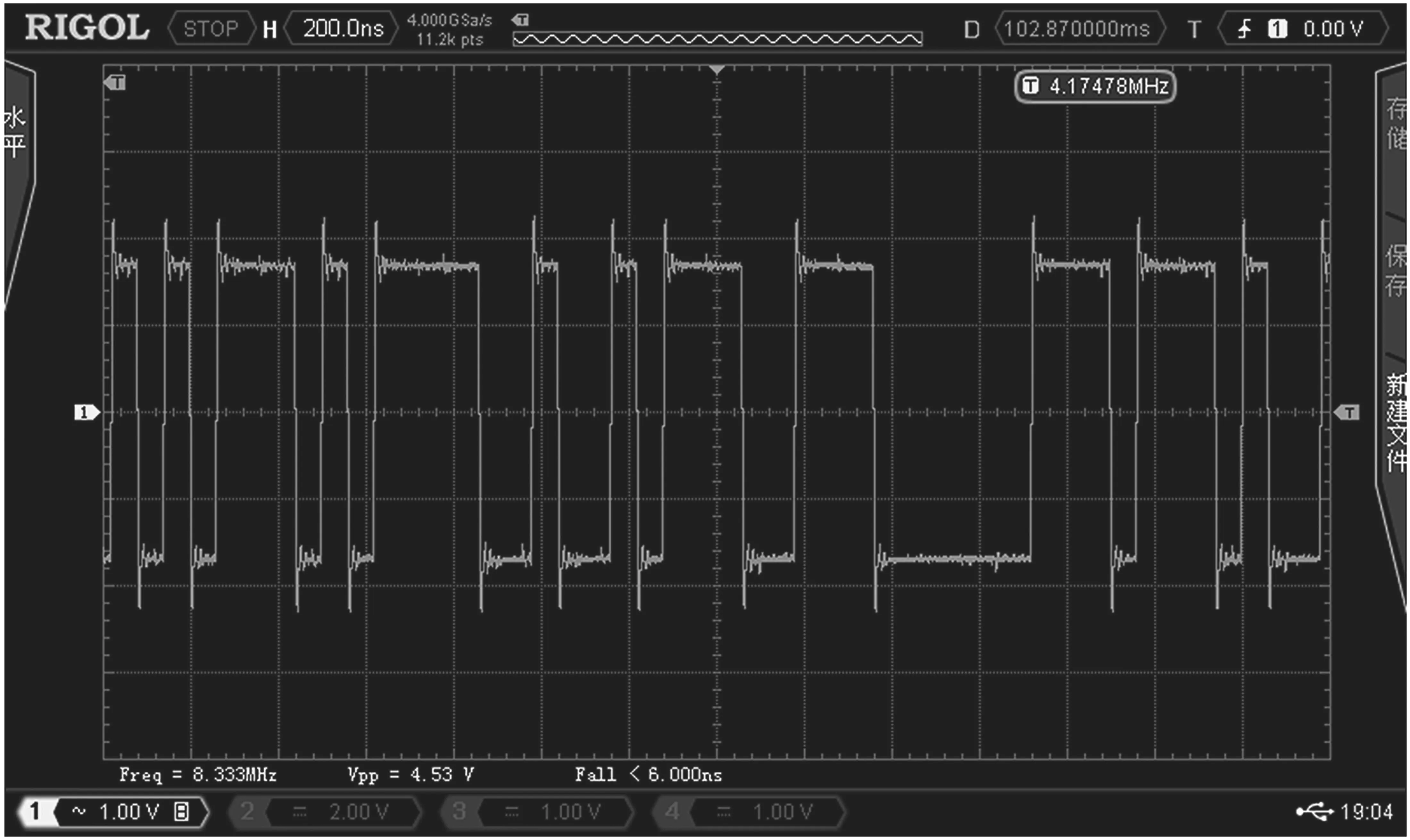
图6 随机序列时域波形

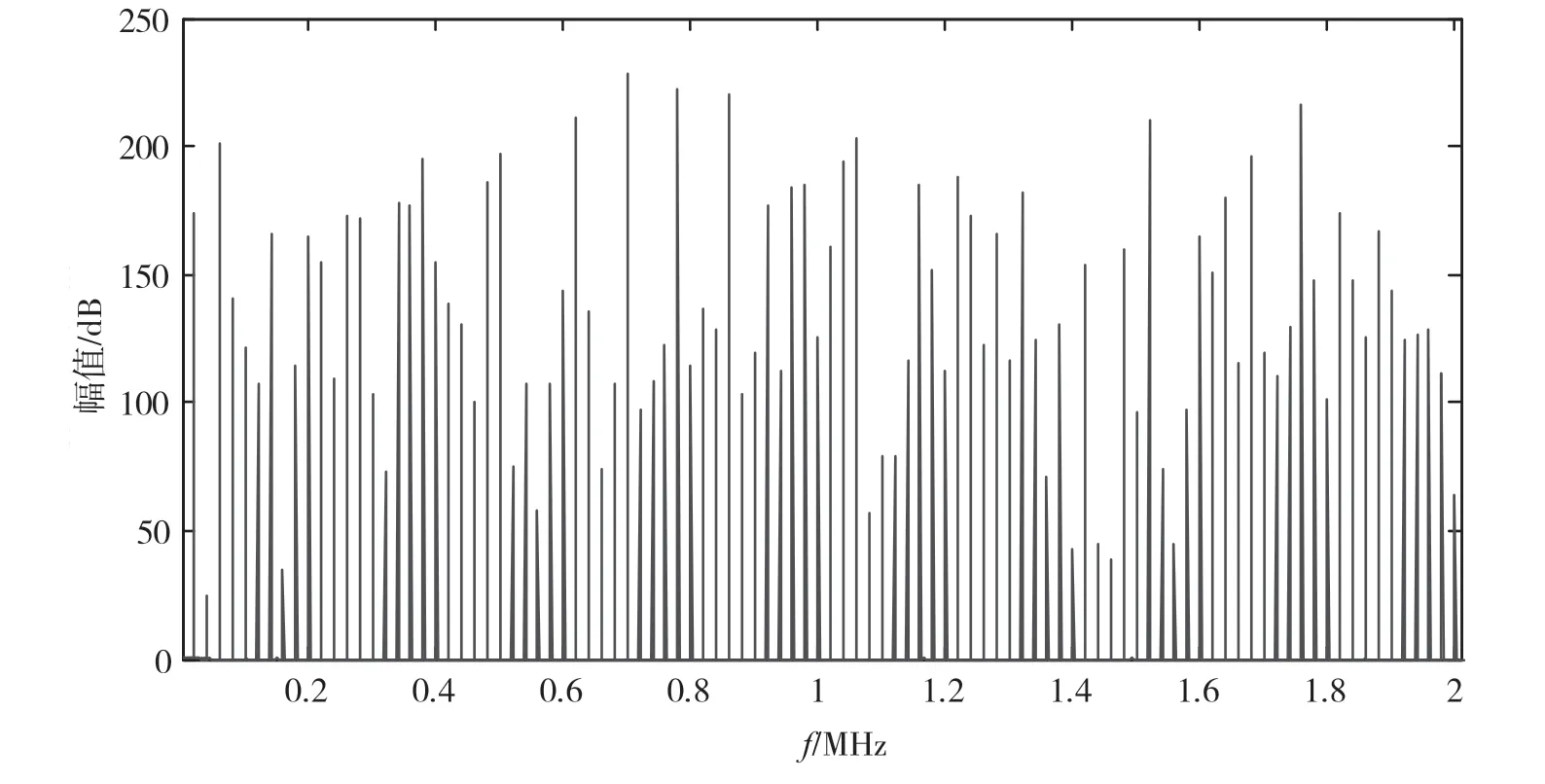
图7 随机序列频谱

2.2 功分器设计

功分器的作用主要是为了解决直接将型号分为4 路造成的阻抗不连续，从而带来的信号发射。为了有效地改善增益平坦度，在功分器和乘法器之间加入了宽带无源幅度均衡器。功分器全称是功率分配器，可以将一路输入信号的能量平均分配到多路输出信号中。功分器主要从频率范围、隔离度、插入损耗、相位平衡性、幅度平衡性等几个参数去分析。综合各种参数分析，功分器选用Mini-Circuits公司的AD4PS-1+。AD4PS-1+为工作频率范围在1～500 MHz，输入阻抗为50 Ω 的无源贴片器件。信号最大输入功率为0.5 W，理论上四路输出之间相位差可为0°，典型隔离度值为30 dB，输入端电压驻波比为1.12，输出端电压驻波比为1.10。

2.3 混频器的设计

一路信号分为四路之后，每一路首先要经过一个乘法器，该乘法器的作为MWC 系统的混频器使用。信号与随机序列相乘，完成的功能是信号频谱的搬移。乘法器选用亚德诺半导体（Analog Devices Inc.）公司的AD835。

AD835 是一个四象限，电压输出模拟乘法器。它的-3 dB带宽为250 MHz。乘法器结构如图8所示。

它的转移函数为：

AD835 为高输入阻抗器件，所以在考虑功分器与乘法器相连时，可以把乘法器输入端看作开路。AD4PS-1 输出端接一个到地的50 Ω 电阻，然后与乘法器相连即可。AD835 输入端电压范围为-1～1 V。因前面功分器为1/4 功率分配，所以功分器端差分电压范围为-2～2 V。

图8 乘法器结构

另外，AD835 的输出阻抗比较低，带负载能力较强，且输出电压摆幅在-2.5～2.5 V。乘法器是一个非线性器件，会带来一定的谐波失真。当U=1、Z=0 时，有：

混频电路的设计如图9 所示。

图9 混频器电路设计

2.4 低通滤波器的设计

在MWC 系统中，随机序列和信号混频之后包含具有一定能量的很多高次谐波。在整个的频谱范围，有相当一部分高次谐波是超过所设定的采样率fs的，而且具有不可忽略的能量。故需要设计一个过渡带窄，阻带外衰减能力强的高性能低通滤波器。这也是MWC 系统实现过程中的一个难点和重点。

常用的模拟低通滤波器有巴特沃斯和切比雪夫及椭圆型滤波器，前两种低通滤波器的传输函数都是一个常数除以一个多项式，为全极点网络，仅在无限大处阻带衰减为接近零。椭圆函数滤波器在有限频率上因为既有零点又有极点，零、极点在通带和阻带产生等纹波，阻带内的有限传输零点减小了过渡带，可获得极为陡峭的衰减曲线。也就是说对于给定的阶数和纹波要求，椭圆滤波器能获得较其他滤波器更窄的过渡带宽，就这点而言，椭圆滤波器的矩形系数是最优的。椭圆滤波器，在通带和阻带是等纹波的一种滤波器。相比切比雪夫滤波器，它是同时用通带和阻带的纹波起伏为代价来换取更为陡峭的过渡带。椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下，有着最小的通带和阻带波动。它在通带和阻带的波动相同，这一点区别于在通带和阻带都平坦的巴特沃斯滤波器，以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。

本系统以音频作为测试信号，故设计低通滤波器截止频率为50 kHz，输入阻抗100 Ω，输出阻抗1 kΩ。为了更好地抑制高频噪声，采用两级七阶低通椭圆滤波器级联，并在无源低通滤波器后增加阻抗隔离电路，以增强滤波器电路的可靠性。椭圆滤波器电路设计如图10 所示。

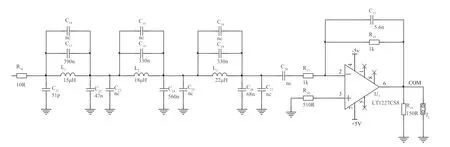
图10 7 阶无源椭圆滤波器

本设计的软件部分和硬件部分均采用模块化设计，大大减少了硬件资源的利用。除了必需的数据采集口和数据输出外，AD 同RAM 和RAM 同UART 之间的接口，都在程序内部做了处理，不占用实际IO 资源。MWC 系统硬件电路如图11 所示，随机序列输出也是通过此部分完成的。

图11 MWC 系统硬件电路

2.5 实验结果验证

为了验证对信号的恢复效果，设定输入信号为单一频率20 kHz 的接近音频范围内的模拟信号。该信号由信号发生器产生，奈奎斯特采样率为8 MHz，采样通道数量为4 路同步采样，采样率fs=fp=40 kHZ。为了方便数据的处理和传输，首先将AD 转换后得到的数字序列存储到由M4K 块配置的单口RAM，然后利用MATLAB 读取串口的采样数据，并根据正交匹配追踪OMP算法对信号进行恢复。恢复的结果如图12 所示。其中图12（a）是原始信号，为了方便与恢复后的信号对比，直接利用MATLAB产生。从图12 可以看出，重构的信号在时域比较接近原始信号，从而验证了MWC 采样系统的信号恢复性能。

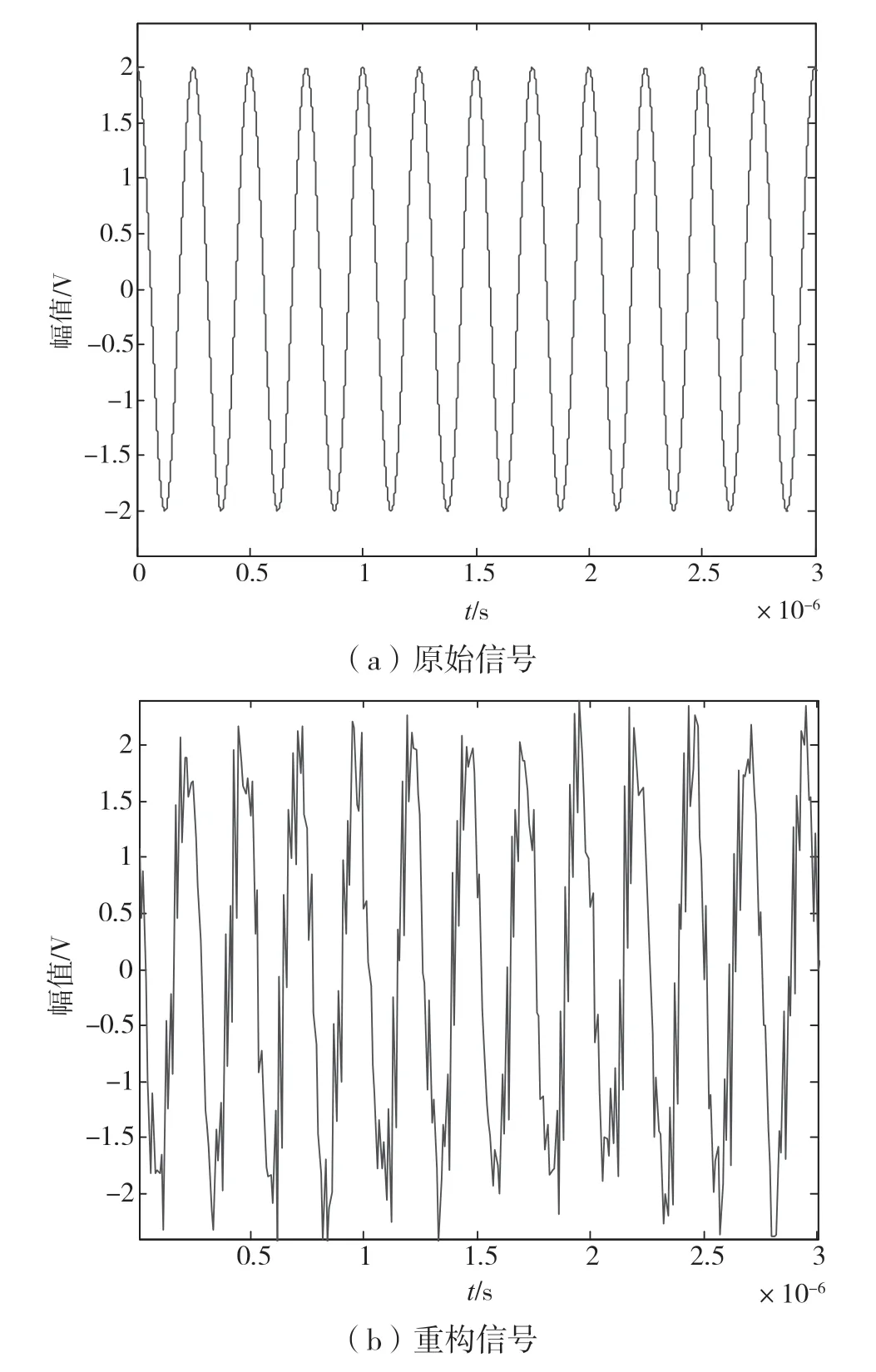
图12 重构信号

3 结语

传统的模拟解调无法对多频带宽带信号进行有效地处理，时间交叉式采样和周期非均匀采样受限于AD 器件本身的跟踪保持电路，必须保持较高的奈奎斯特频率。本文利用具有严格时序特性的FPGA 产生伪随机序列，完成对多频带信号频谱搬移，结合MWC 系统和Xampling 算法，真正实现了利用低速AD 对宽带多频带信号的降采样，完成了一套对稀疏多频带信号利用远低于奈奎斯特采样率进行采样和信号盲恢复系统地设计。为解决目前商用AD 难以满足现代通信模数转换需要高采样率，提供了一套行之有效的解决方案。