浅析初中数学教学中数学建模思想的渗透

郑 忠

(福建省三明市尤溪县管前中学 福建 尤溪 365116)

前言

初中时期乃是学生形成建模思想的黄金阶段，而且还是发展初中生的抽象能力的关键时期。如今，在数学教学与学生学习当中已经提到，人们在从数据到演绎再到应用这个周而复始的周期当中应用着数学，从中能够体会到数学建模具有的重要性。初中生对数学知识加以分类，对实际问题加以解决之时，可以选择相应的数学模型来对问题加以解决，将知识划归到已有的知识体系当中，对知识具有的内涵和意义进行深入理解，这样可以帮助初中生对数学知识具有的应用价值进行体会，对知识学习和数学建模这一思想的逐渐形成拥有着重要意义。

1.创设问题情境，激发初中生的建模兴趣

在初中阶段的数学课堂上，教师可创设良好课堂问题情境，调动初中学生的自主性、积极性与探究问题的欲望，从而激发初中学生求知欲望，促使其主动投入到学习之中。此外，教学期间，数学教师还需注重培养初中生建模能力，通过营造问题情境，结合初中生学习经验，激发初中生学习兴趣，之后构建相应的数学模型，进而在提高初中生的学习效率这一基础之上，有效提升课堂教学效果。

比如，秀丽服装公司当前拥有甲与乙两种布料，两种布料分别由42米与30米，计划使用两种布料制作某中学的学生校服共40件。已知每制作一件M码的校服需要耗费甲种木料0.8米，乙种布料1.1米，可以获利45元。而每制作一件L码的校服需要耗费甲种木料1.2米，乙种布料0.5米，可以获利30元。假设秀丽服装公司共制作x件M码校服，一共获利元，该公司共有多少种制作方案？哪种方案获利最大？最大利润为多少？

分析：

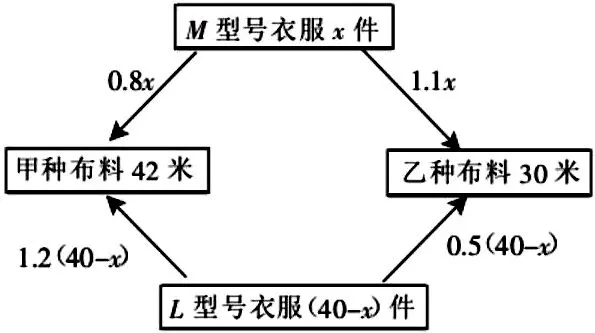
解得15≤x≤16，x取15、16两个整数。

因此存在两种方案：

方案一：生产15件M码衣服，25件L型号的衣服。

方案二：生产16件M码衣服，24件L型号的衣服。

根据题意能够得出关系式：

当x=16之时，y=240+1200=1440.

所以，当生产16件M码的衣服，24件L码的衣服时，秀丽服装公司的获利是最大的，最大利润为1440元。

2.把实际生活当作背景，培养初中生的建模意识

众所周知，数学知识源自现实生活，同时在实际生活当中有着重要应用，数学知识与生活存在紧密关联。所以，教学期间，数学教师需把实际生活当作背景，积极培养初中生的建模意识以及数学思维。

例如，欧亚商场春节期间正在售卖一品商品，已知该商品进价为20元，售卖期间发现此种商品售价x与每日销的售量y间具有如下关系：

x3 5 9 11

y18 14 6 2

(1)在所给坐标系当中：

I、按照表中给出数据描绘实数对(x,y)的对应点。

II、猜测且得出确定的每日销售量y与售价x间的函数关系式，画出相应的函数图像。

(2)设欧亚商场售卖此种商品每天的获利情况，按照每天的销售规律，回答以下问题：

I、求出每天商场销售利润p元和售价x间的函数关系，问每日的销售利润p是否有最小值。如果有，求出最小值；假设没有，说明理由。

II、在给出的坐标系当中，画出销售利润p元和售价x元间函数图像，并且通过图像观察写出销售利润p元和售价x的取值范围。

解：(1)在所给坐标系当中描绘出四个点的位置。

猜想该函数为一次函数y=kx+b，把点(3,18)与点(5,14)代入到上式之中，可以得到k=-2，b=24，进而得到一次函数为y=-2x+24.把(9,6)与(11,2)代入其中可知，亦满足。

所以，所求函数为y=-2x+24(0≤x≤12).

(2)因为销售利润=售价-进价，因此p=xy-2y.

把y=-2x+24(0≤x≤12)代入可得到：

p=y(x-2)=(24-2x)(x-2)=-2(x-7)+50

当x=7时，每日销售利润的最大值是50元。

当x≥12时，也就是售价是12元或者大于12元时，无人购买，因此此时利润是0.

根据实际意义可知，当x=0时，也就是亏本卖出，这是利润是-48，也就是最小值。按实际意义，当0

当x=2或者x=12时，利润是0；

当x>2时，价格太高，没人购买，所以利润为0.

根据图像可知，x>0，-48

结论

综上可知，建模思想是数学方面核心素养当中的重要内容，实际教学期间，数学教师需积极对建模思想加以渗透，这样不仅能够提升初中生的解题能力，同时还能培养初中生的数学思维。为此，课堂之上，教师需对不同建模方法进行讲解，强化初中生对建模思想的运用意识及能力，进而有效培养初中生的建模素养与能力。