基于ESDA 的中国汽车产业空间演变研究
李洪庆 康凯 刘磊
(中国汽车技术研究中心有限公司情报所)

汽车产业是推动新一轮科技革命和产业变革的重要力量,是建设制造强国的重要支撑,是国民经济的重要支柱[1]。欧美日韩等发达国家的汽车工业发展较为成熟,伴随着技术革命的推进和生产力的提高,汽车工业布局不断变化,产业集聚程度日益提高。很多学者[2-3]从产业集聚的视角对汽车工业布局进行深入研究,探讨区域发展的平衡程度对资源间割裂的影响。文献[4]等对德国汽车制造业空间布局进行了研究,文献[5]对澳大利亚汽车制造业空间布局进行了研究。在国内,文献[6]对汽车产业省区专业化进行了研究,文献[7]对我国汽车产业布局的时空变化规律进行了探讨。伴随着不同分析方法、不同研究尺度的探讨,汽车产业的空间布局的研究方法也在不断的成熟。然而,任何事物与其周围事物都存在联系且与其相近事物的联系更为紧密,几乎所有空间数据都具有空间依赖性或空间自相关特征[8-9],因此对中国汽车产业空间演变规律研究具有重要的意义。探索性空间数据分析(Exploratory Spatial Data Analysis,ESDA)是以空间关联性测度为核心的空间数据分析方法和技术的有效结合,通过对数据进行可视化,揭示空间集聚状态和相互作用机制。文章以我国整体为研究对象,以31 个省、市、自治区为研究单元,基于1983、1995、2006、2018 年中国汽车生产省域统计数据,通过全局和局部自相关分析方法对中国汽车生产空间布局进行分析,分别从不同权重矩阵和时间纬度研究全局自相关,从Moran 散点图和LISA 集聚分布研究局部自相关,从而获取中国汽车生产的空间依赖性和分异特征。
1 数据来源与研究方法
1.1 数据来源
文章中的研究数据主要来自《中国统计年鉴》、《中国汽车工业年鉴》、各省市区的统计年鉴、国家统计局、中国汽车工业信息网、中国汽车工业协会等。数据共涉及我国31 个省、市、自治区。
1.2 研究方法
1.2.1 全局空间自相关指标
根据地理学第一定律,任何事物都不是孤立存在的,事物之间必然存在某种关联,只不过距离相近的事物关联会更加凸显[10]。全局空间自相关可以衡量区域整体的空间差异和空间联系,以便判断研究对象即文章研究的汽车生产是否存在空间集聚,文章采用Global Moran's I 指数用于表示空间聚集程度,其计算公式为:


n——所研究的省域总数;
wij——空间权重值。
莫兰指数是一个有理数,经过方差运算后,得到的值会被归一化处理到-1 和1 之间,当I<0 时表示空间负相关,其值越小,空间差异性越大,随着自变量的增长,因变量随着减少,即汽车生产空间特征呈现为高值区和低值区相邻的分散状态;当I>0 时表示空间正相关,其值越大,空间相关性越强,随着自变量的增长,因变量也随着增长,即汽车生产空间特征呈现为高值区和高值区或者低值区和低值区相邻的集聚状态;当时表示不存在关联性,区域间为随机分布,即省域汽车生产不存在空间相关性。
1.2.2 局部空间自相关指标
全局空间自相关是从整体角度来说明不同区域之间差异的平均程度,但是对于区域内部之间的差异性无法有效进行量化描述,即空间依赖性。为了全面反映中国汽车生产省域之间的空间集聚程度,文章采用Moran 散点图和LISA 统计指标来考察局部的相关性差异。
1)Moran 散点图。Moran 散点图通常用来研究局部空间不稳定性,横坐标为变量向量,纵坐标为变量的空间滞后向量,Moran 散点图既可以检测局部空间是否存在关联及探索全局空间关系,还可以将分析结果使用二维图可视化。Moran 散点图的第一和第三象限表示空间正相关,观测值相近的区域出现集聚,第二和第四象限表示空间负相关,有差异的观测值区域出现集聚现象。
2)LISA 统计指标。LISA(局部莫兰指数)统计指标的本质是将全局莫兰指数分解到各个区域单元,可以反映出不同空间位置汽车产量是否存在空间集聚现象,并在结果地图上显示出异常区域,有助于对局部空间特征更为深入的研究,其计算公式如下:

sx——xi和xj对应的标准差。
如果Ii>0 而且zi>0,说明省域处与周边省域的汽车产量的观测值都为高值区,属于Hight-Hight 集聚;如果Ii>0 而且zi<0,说明省域处与周边省域的汽车产量的观测值都为低值区,属于Low-Low 集聚;如果Ii<0而且zi<0,说明省域处的观测值远高于周边省域的观测值,属于Hight-Low集聚;如果Ii<0 而且zi<0,说明省域处的观测值远低于周边省域的观测值,属于Low-Hight集聚。
通过将Moran 散点图和LISA 统计指标有效的结合起来,可以更好的对省域空间依赖性和空间分异特征进行描述。
1.3 空间权重的构建
在空间权重矩阵构建中,最常用的是基于邻接和距离的原则,在充分考虑中国的行政区域划分的基础上,重点对Rook 邻接规则、距离规则和k-nearest 邻近规则进行探讨和选择。
1)基于Rook 邻接的空间权重。Rook 邻接规则认为只要2 个区域有一段共同的边界即认为2 个区域相邻。GeoDa 软件提供的Rook 高阶邻接规则,为文章中的权重选择提供了更为准确的算法。如果wij=1,则表示2 个空间单元之间有一段相同边界;相反wij=0。

2)基于距离的空间权重。距离规则的优点在于充分考虑距离的相对大小,从定量的角度刻画空间邻接性,距离规则空间依赖关系可以分为非几何距离和几何距离,几何距离分为有限距离、负相关距离和混合距离,文章根据中国省域汽车生产现状选取有限距离,即2 个空间单元之间的集合距离小于开始设定的阀值d时,则wij=1;相反wij=0。
式(3)基于k-nearest 邻近的空间权重。k 最近邻规则是一个理论上比较成熟的规则,在运算中认为所有的区域都是已经正确分类的对象,这种规则在一定程度上避免了Rook 邻接规则和距离邻接规则设立最小阀值而导致部分有效区域无法进行计算的问题。
2 实证分析
2.1 汽车生产空间分布变化
1983 年至今,中国汽车产量生产规模总体呈现上升态势,各省域范围内的变化幅度不一,特别是在2001 年后,中国汽车产量呈现高速增长态势,不同省份在不同年份之间的变化差异很大。这表明,中国汽车产量在不同的分析维度上有不同的空间集聚形态。
从地域角度上看,从1983 年至今我国汽车产业生产布局符合胡焕庸线[11](既黑河—腾冲一线)分布特征,汽车生产集中在东部,西部区域汽车产业布局较少。从时间维度上看,中国汽车生产有向聚集区转移的趋势,并逐步呈现出集聚现象,表现为东西分异。到1995 年,由于四川成都龙泉驿区、上海嘉定区、广西柳州柳东新区汽车产业的快速发展,带动了3 个省市的汽车产量突飞猛进。到2006 年,重庆两江新区和巴南区,以及广州增城区和花都区的异军突起,使得两地的汽车产量在全国名列前茅。2018 年的汽车产量布局与2006 年相差不大,格局基本一致。中国汽车生产的重点已经向东部转移,空间集聚效应存在于省域之间。
2.2 中国汽车产业全局自相关分析
2.2.1 不同权重矩阵下的全局自相关分析
为了更准确地建立中国汽车生产全局自相关模型,文章通过在不同的空间权重矩阵下,对2006 年汽车生产数据进行验证,以期得出最适合模型的空间权重矩阵。如表1 所示,分别在Rook 规则下的r1、r2 和r3,距离规则,以及k 最近邻规则下的k4、k6 和k8,进行全局自相关检验,得出2006 年中国31 省市区汽车产量分析的Moran's I 指数及其对应的Z 值和P(概率)值。r1 规则表示在1 阶Rook 规则下区域相邻,r2 规则表示在2 阶Rook 规则下区域相邻,即相邻的相邻也默认为相邻,r3 同理;在距离规则下,由于阀值的限制,每个省域最少会有一个省域和它相连接;k4 表示在k-nearest 规则下确定每个省域都有4 个省域和它相邻,k6 则表示每个省域有6 个邻近关系,k8 则表示每个省域有8 个邻近关系。

表1 不同权重矩阵下Moran 指数
由表1 可以看出在7 种不同空间权重规则下Moran's I 全为正值,说明中国汽车生产呈现空间正相关,随着省域周边观测值的升高或者降低,会对省域自身空间差异带来相同影响。其中在k4 权重矩阵下,P值具有统计学差异,Moran's I 最大;中国汽车生产的空间相关性随着邻接关系的增多反而逐渐减弱。在k4 空间权重矩阵下,空间相关性最强,Moran's I 为0.151;在Rook 和k 最近邻权重矩阵下,虽然也存在一定程度的空间相关性,但随着邻接关系的增加相关性减弱;综合7 种不同权重规则下的Moran's I、Z 值和P 值,全局自相关分析选择k4 权重矩阵。
2.2.2 不同时间维度上的全局自相关分析
分别对1983—2018 年36 年跨度的数据进行分析,进一步探讨汽车生产空间集聚演变情况。表2 为1983-2018 年各省市区汽车产业的全局Moran 指数,图1 为1983-2016 年中国汽车产业的Moran's I 变化情况。
计算结果显示,在正态分布假设下,1983—2018 年中国汽车生产的全局Moran's I 指数除了1994 年和1995 年Moran's I 为负值,均为正值,这说明中国各省市区汽车生产受到邻近区域汽车生产的影响,省域汽车生产空间呈现为高值区和高值区或者低值区和低值区相邻的情况。因此,在省级尺度上中国汽车生产具有空间正相关性特征较强,即省域汽车生产空间分布呈现聚集状态,而不是随机分布。
从表2 和图1 可以看出,就1983—2018 年研究时段,我国汽车生产集聚程度大致可以分为3 个阶段:1983—1995 年为第1 阶段,Moran's I 呈现波动下滑趋势,即随着时间的推移汽车生产省域空间相关性不断降低;1995—2005 年为第2 阶段,Moran's I 从-0.004上升到0.166,增幅达0.17,集聚度有较大提高;2005—2018 年为第3 阶段,Moran's I 由0.166 降至0.062,工业集聚程度逐渐降低。由此可知,中国汽车生产总体发展水平在空间上呈现一定的集聚现象(高高集聚或者低低集聚),但并不是特别显著,空间相关性随着时间的推移在减弱,整体空间布局呈现空间扩散状态。

表2 1983-2018 年各省市区汽车产业的全局Moran 指数

图1 1983-2016 年中国汽车产业的Moran's I 变化情况
2.3 中国汽车产业局部自相关分析
Global Moran's I 指标属于全局统计指标,在进行空间相关性分析中往往难以揭示空间内部的差异性,通常会出现空间整体差异较小,但是局部空间差异较大。因此,为了全面反映中国各省域汽车生产空间差异情况,探讨其局部相关性,利用Moran 散点图和LISA 分布来对局部空间依赖性和分异特征进行分析。
2.3.1 Moran 散点图
1983、1995、2006、2018 年31 个省市区的空间Moran 散点分布图,如图2 所示。
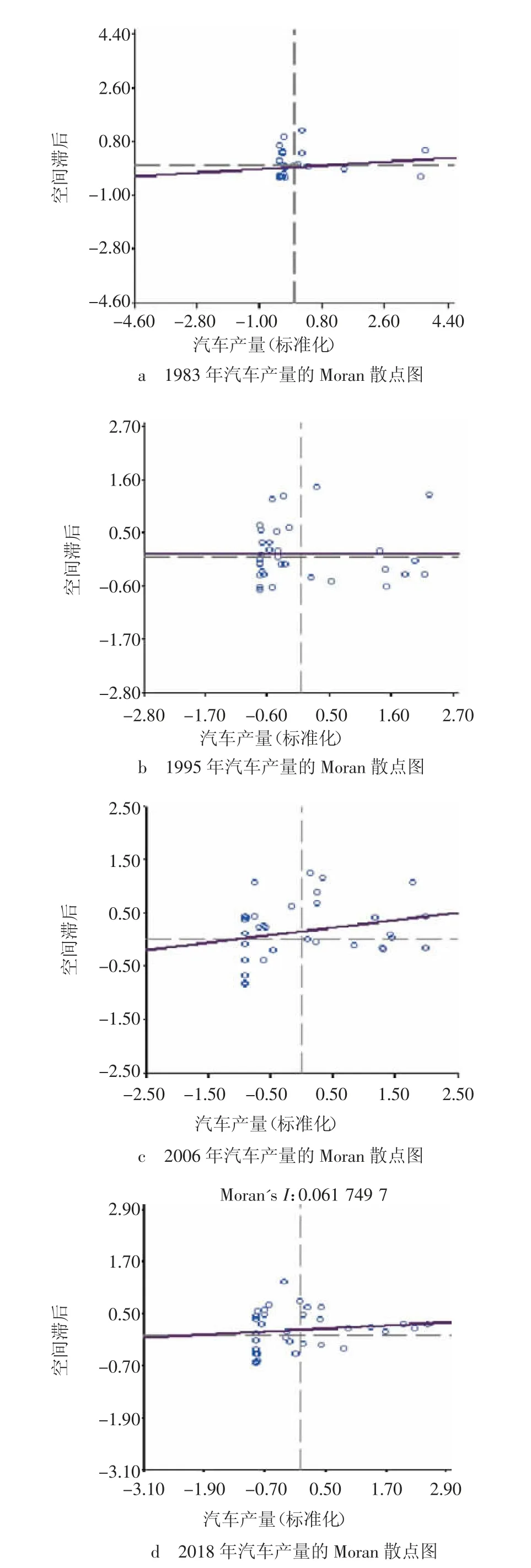
图2 1983、1995、2006、2018 年汽车产量的Moran 散点图
可以看出,在第一、三象限的省域个数,从1983 年的19 个减少到1995 年的12 个,后又增长到2006 年的17 个,2018 年的19 个,2018 年第一、三象限省域个数占总数的61%,表明中国汽车生产在地理上呈现为空间正相关。
Moran 散点图显示出,不同年份中国汽车省域生产集聚特点有着较大的差异,主要是因为近几十年各省积极将汽车产业确立为支柱产业,各省域发展程度各异。我国汽车生产出现明显的东西差异,处于第一象限的省域全部位于东部地区,第三象限的省域主要位于西部;从1995 年的Moran 散点图可以看出,处于第一象限的地区向东北部转移,处于第三象限的区域向中部转移;对2006 年Moran 散点图进行分析,中国汽车生产的总体格局呈现出与1983 年相似的东西差异特征;从2018 年的Moran 散点图可以看出,处于第一象限的地区新增中部省域,主要有重庆、湖北等省,处于第三象限的区域主要还是集中在西部。
2.3.2 LISA 集聚分布
汽车生产的LISA 指标可以用来衡量省域单元和周边单元相异(负相关)或者相近(正相关)的程度。本节使用Geoda 软件,分别计算了1983、1995、2006、2018 年汽车产量的LISA 指标(p=0.05)。
如表3 所示,在p≤0.05 的显著水平下可以得出从区域整体来看,中国汽车生产存在局部的空间集聚特征,各省域和周边省域之间有一定相关性。

表3 局域空间自相关显著性省区统计表
从统计的省域数量上来看,很多省域的空间关系并不显著,不显著省域表示这些省域和周边省域汽车产量之间的相互影响程度较小,在显著省域中,大部分表现为空间正相关。由表3 可知,从1983 年到2006 年显著性省域呈现上升趋势,表明国内汽车生产空间集聚现象逐渐加强。但是在2018 年,仅有湖南表现为低高聚集区。这表明我国汽车生产空间聚集现象逐渐减弱,呈现扩散状态,出现这种状态是因为2013 年开始我国汽车产量突破2 000 万辆,在2017 年达到研究时段的峰值2 901.81 万辆,在所研究的31 个省市区中,有28 个将汽车产业确立为支柱产业。
3 结论
文章通过空间探索分析方法(ESDA),分别采用全局自相关(Global Moran’s I)、局部自相关测度指标(Moran 散点图、LISA 统计指标)对中国汽车生产空间布局的变化进行了实证分析。结果表明:1)1983—2018年我国汽车产业生产格局符合胡焕庸线(既黑河—腾冲一线)分布特征,中国汽车产业生产有聚集的明显趋势,并且东西分异现象明显;2)1983—2018 年中国汽车产业分布除1994 年和1995 年外均呈现正向空间依赖性。通过对2006 年汽车产量进行7 种不同的邻接规则分析,均显示中国区域汽车产业受相邻区域汽车生产状况的正向影响,相似值之间存在地理集聚现象。1983—1995 年和2005—2018 年间,空间自相关性出现下降,1995—2005 年间出现上升,集聚度有较大提高;3)Moran 散点图的分析结果显示,位于第三象限的省域单元随着时间的推移呈现出向周边扩散的发展态势,位于第一象限的省域不同时间区间变化较大;4)对LISA 集聚分布的分析结果显示,中国汽车生产在局部呈现出明显的空间聚集性,与Moran 散点图的分析结果一致。从数量上来看,大部分省域的空间关系并不显著,在显著区域表现出正向关系的比例较大。从空间视角看,高聚集区主要存在于我国东北区域。

