高地温影响下的水工隧洞围岩应力变形规律分析
后雄斌
(新疆水利水电勘测设计研究院,乌鲁木齐 830000)
0 前 言
随着国家经济社会的高速发展,地表浅部资源、可活动空间严重减少。为满足国民经济的可持续发展,能源、资源和人类活动空间的开发和利用从地层表面持续转向地下深处。地下深处往往存在着不良特殊地质情况,从目前已建及在建的地下工程中可以发现,高地应力、高地热、高渗压水及岩爆等特殊环境下的不良地质情况在工程建设中时常出现。相对于常规地表工程建设而言,在这些不良地质环境下建设各类地下工程难度更大、面临问题更多。因此,研究特殊环境下水工隧洞围岩可能面临各种情况下的应力变形情况就显得尤为重要,可为类似地下工程的建设提供一定的参考。
目前,国内外专家针对复杂特殊情况下的水工隧洞受力变形开展了大量研究,取得了众多科研成果。如张岩等[1]从多个方面考虑,针对某高地热引水发电隧洞,通过数值试验研究了温度场、围岩类别、隧洞埋深对围岩应力场和位移场的影响,其研究结果表明,工程遇到的高温可以使得隧洞边拱处压应力及顶部向下位移减小,隧洞埋深越大,其关键部位的应力和位移均会在一定程度上增大。刘文岗等[2]针对高发射废物处置库巷道,根据热-力耦合作用下花岗岩温度场分布及应力计算结果,设置了废物处置库巷道合理的设计间距。宿辉等[3]针对隧洞开挖后初次支护喷射混凝土与开挖面之间的粘接强度,采用试验的方法对其进行了细致研究。杨平平[4]通过CFD建立模型,研究了风速对隧道温度场的影响,采用物探超前预报、超前水平钻探结合方法预测温度。PAN等[5]采用有限差分法、细胞机法比较全面的研究了岩体三维热-力耦合特性。周广磊等[6]采用COMSOL有限元数值软件对自行建立的温度-应力耦合脆性岩石模型进行了二次开发,并对开发模型进行了验证,同时研究了岩石轴向应变和声发射累计数之间的关系。白冰[7]借助有限元分析软件,采用自定义非等温条件本构模型,研究了黏土地层中核废料储存库周边土体物理力学场的变化规律。上述学者虽从数值模拟、模型试验、现场试验及理论推导等方面对某一特定环境下的岩体受力变形情况进行了研究,但很少将工程可能遇到的高地热环境问题考虑在内。
鉴于此,本文针对高地热环境下的水工隧洞,从平面空间角度出发,研究不同方位路径、围岩深度、温度变化、地层深度、侧压力系数影响下的隧洞围岩应力变形特征,为类似工程支护结构、保温隔热、降温措施设计以及深部岩体温度应力变形预测等提供依据。
1 热-力耦合本构关系
岩体内部无热源时,热量传输微分方程为:
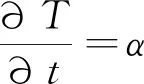
(1)

式中:α为热扩散系数,m2/s;λ为热传导系数,W/m·℃;c为比热,J/kg·℃,即单位质量物体温度升高1 ℃所需要的热量;ρ为体力密度,kg/m3;▽2为拉普拉斯算子。
温度与外力环境作用下用位移表示的岩体(应力)平衡方程为:
(2)
温度场作用下的岩体弹性本构方程为:
σii=λθ+2μεii-3KβT
τij=μγij
(3)
式中:θ为体积应变;λ和μ为拉梅常数;β为热膨胀系数, ℃-1;T为温度,℃;K为体积变形模量;F为外力,N。
2 数值计算模型
2.1 数值算例
地处新疆边远地区的某工程是一座具有防洪、发电、灌溉和改善生态环境等多种用途的山区控制性综合水利枢纽工程。该工程引水发电隧洞施工过程中遭遇高温、岩爆等特殊地质情况。引水隧洞为圆形断面,开挖洞径8.6 m,洞身周边岩体为中厚层状的坚硬云母石英片岩夹石墨片岩,围岩类别为Ⅲ类,隧洞最大埋深约450 m,最小埋深约100 m。现场实测资料显示,该工程引水发电隧洞穿越多条断层构造带,且隧洞前段存在约4 km的高温地段。施工现场掌子面钻孔实测温度异常,已超过100 ℃,个别岩体裂隙中有水蒸汽冒出,未见地下水出露。为此,本文采用有限元分析方法,对不同温度边界、隧洞埋深、侧压力系数等情况下的高地温引水隧洞围岩应力变形特征进行分析计算。
2.2 计算参数
有关研究表明,温度对岩石的物理力学参数会产生一定的影响。为保证分析结果的准确性、可靠性,研究过程中考虑了温度对岩石计算参数的影响。考虑到该工程钻孔最高温度超过100 ℃,运行期温度0~5 ℃的特殊情况,特设定开挖后洞内侧温度为Inner=5、10 、20、25、30 ℃,围岩深部温度为Outer=60、70、80、100、105 ℃。根据隧洞实际埋深,特选定depth=100、200、280、350、500 m埋深进行分析。λ依据《水利水电工程地下建筑物设计手册》和DL/T 5057-2009《水工混凝土设计规范》[8-9],温度和压力均会对岩石基本力学性质产生影响,且各类岩石的泊松比随温度和压力的变化情况各不相同。故本文拟定侧压力系数依次为λ=0.1、0.3、0.5、0.6、0.75、0.9、1.0的情况进行有关分析研究。模型计算参数如表1所示:
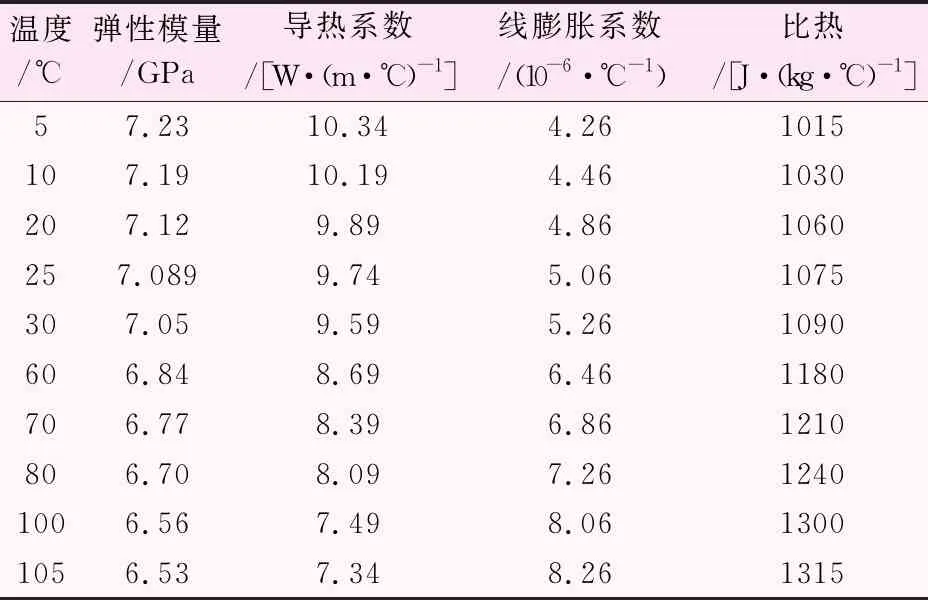
表1 围岩的力学及热学参数表
2.3 计算模型及边界条件
根据工程实际,研究过程中不考虑地下水的影响,选取引水隧洞周边一定范围深度,将其视为半无限域问题,采用有限元方法进行求解。考虑到该隧洞沿线地应力水平较低,围岩条件较好的硬质岩,同时,本文主要研究的是引水隧洞围岩热-力耦合作用下的应力变形规律,因此,隧洞有限元计算模型采用弹性模型。模型中考虑温度对岩石材料物理力学参数的影响,通过单元生死技术实现隧洞施工过程的模拟,采用修改关键字方法添加*initial conditional, type=stress, input=(处理后的.txt文件)语句实现初始地应力场平衡,模型范围48 m×48 m(长×宽),有限元网格划分如图1所示。模型边界为左右水平约束、上部零自由度、下部水平及竖向2个方向约束。模型上部通过施加与埋深有关的静水压力均布荷载实现不同隧洞埋深工况的模拟。

图1 圆形隧洞计算模型及有限元网格划分图
3 数值分析结果
3.1 隧洞周边岩体平面应力位移分布特征
图2、3分别为隧洞围岩Mises应力云图和位移云图。由图2、3可以看出,围岩应力和位移关于隧洞竖向中心线左右对称,应力值最大值位于侧墙两侧,位移最大值位于拱顶处,侧墙处位移最小。从整体上来看,离开挖面越远,隧洞围岩位移和应力将会相应减小,隧洞开挖卸荷和温度荷载对围岩产生的影响就会越小。

图2 Mises应力云图 单位:Pa
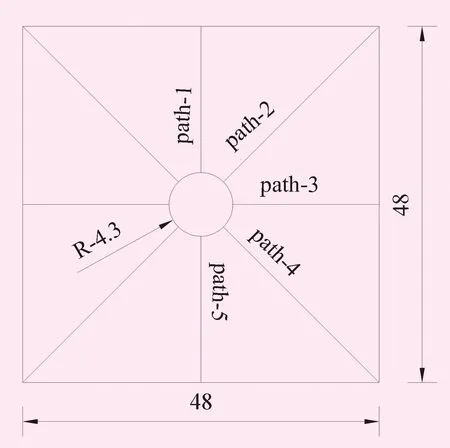
图4 计算路径及几何尺寸 单位:m
为了便于分析隧洞周边岩体应力的空间分布情况,特选取如图4所示的5条路径。图5给出了路径path-1~5的围岩径向应力分布情况。由5可知,不同方位指定路径上隧洞开挖面附近围岩径向应力分布规律一致,总体表现为隧洞开挖面处径向应力为0,离开挖面越远围岩径向应力越大,与变化曲线表现出相同的趋势。同一围岩半径深度处,拱顶径向应力最大,随着距拱顶距离的增加,围岩径向应力不断变小,整个模型径向应力分布关于隧洞水平轴线呈中心对称。不同路径下径向应力随围岩深度的变化呈现出相同规律,即距开挖面一定深度范围内,围岩径向应力增大后趋于稳定,距洞顶越远越趋于平缓,拱顶以上围岩应力变化最为明显。

图5 围岩径向应力
3.3 不同深度范围内隧洞周边岩体应力位移分布特征
图6给出了离隧洞开挖面距离Ri分别为0.92、1.84、2.76、4.37、16.47 m时的围岩环向应力随d/D(D为1/2模型距隧洞开挖面Ri处半圆环总弧长,d为从隧洞拱顶围岩开始的圆弧角度对应的弧长,后文各图中涉及的d/D含义同)的变化趋势。由于荷载及边界条件的对称性,整个围岩环向应力分布关于隧洞轴线左右对称,因此,只对隧洞单侧围岩应力分布规律进行分析。从图6中可以看出,不同围岩深度范围内环向应力分布规律一致,整体上关于隧洞水平中心轴线呈上下对称,同一围岩半径深度范围内拱顶及洞底应力最小,越靠近侧墙中部围岩应力就越大,整体上表现为压应力。从整体上距离洞壁围岩同一深度处,侧墙环向应力最大,拱顶及洞底环向应力最小,且拱顶及侧墙环向应力关于隧洞竖向中心轴线左右对称;不同围岩半径处,围岩环向应力不同,洞壁处环向应力最小,离洞壁越远侧墙附近围岩环向应力就越小,而拱顶和侧墙围岩环向应力就越大,但变化幅度小于侧墙。

图6 围岩环向应力图
由图7可知,同一隧洞围岩深度范围内,侧墙处围岩位移基本为0,拱顶及洞底处围岩位移最大。不同深度范围内,围岩位移随着离隧洞开挖面距离的增加而减小,围岩位移关于隧洞水平向轴线上下对称,从侧墙位置至拱顶或至洞底,位移随环向距离的增加呈现出非线性递增趋势,在拱顶处取得最大值。距隧洞开挖面0.92 m处,围岩位移最大值为6.43 cm;距隧洞开挖面2.76 m处,围岩位移最大值为5.08 cm;距隧洞开挖面4.37 m处,围岩位移最大值为4.16 cm;距隧洞开挖面6.79 m处,围岩位移最大值为3.27 cm;距隧洞开挖面9.21 m处,围岩位移最大值为2.68 cm。
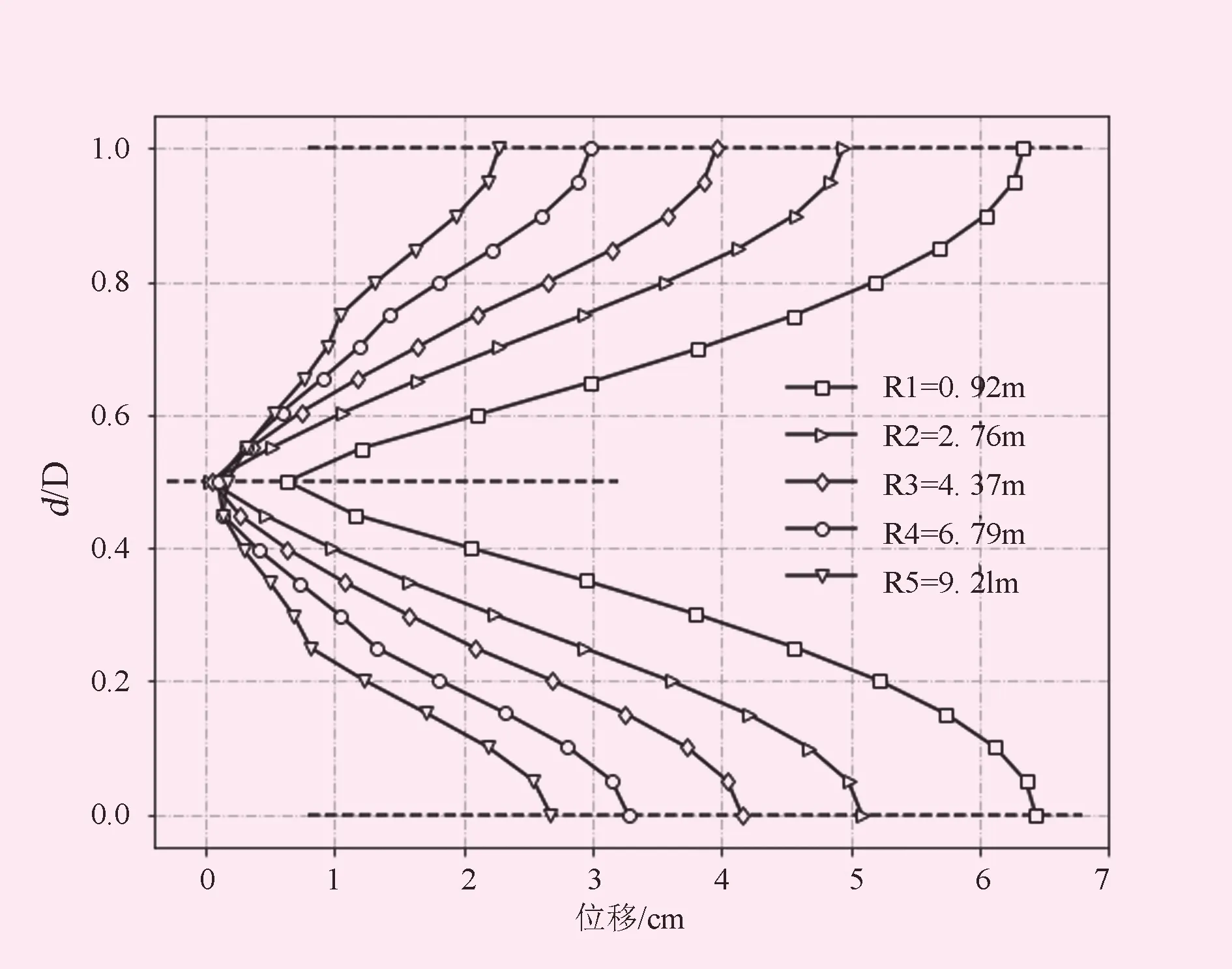
图7 围岩位移分布图
3.3 不同地层环境温度下隧洞周边岩体应力位移分布特征
由图8可以看出,隧洞开挖面处环向应力受内外环境温度影响较小,且关于隧洞水平轴线上下对称。隧洞拱顶和底部环向应力为0,从拱顶或底部沿开挖面环向指向洞身中部的开挖面处环向应力呈非线性递增变化,不同内外侧环境作用下的环向应力在同一部位基本相等。因而,在地下工程建设过程中,洞内环境温度变化时,引起隧洞环向应力的变化可忽略不计。

图8 洞壁环向应力图
由图9可以看出,当隧洞施工时洞内环境温度发生变化时,对隧洞开挖面位移的影响不明显。不同洞内环境温度作用下同一位置的隧洞开挖面位移基本相同。隧洞开挖面处位移关于隧洞水平轴线上下对称,侧墙中部围岩位移为零,越靠近拱顶和洞底,隧洞开挖面处围岩位移越大,在拱顶及洞底处达到最大。可见,洞内侧环境温度的变化会对拱顶和洞底的位移产生较大影响,其余部位的影响可忽略不计。
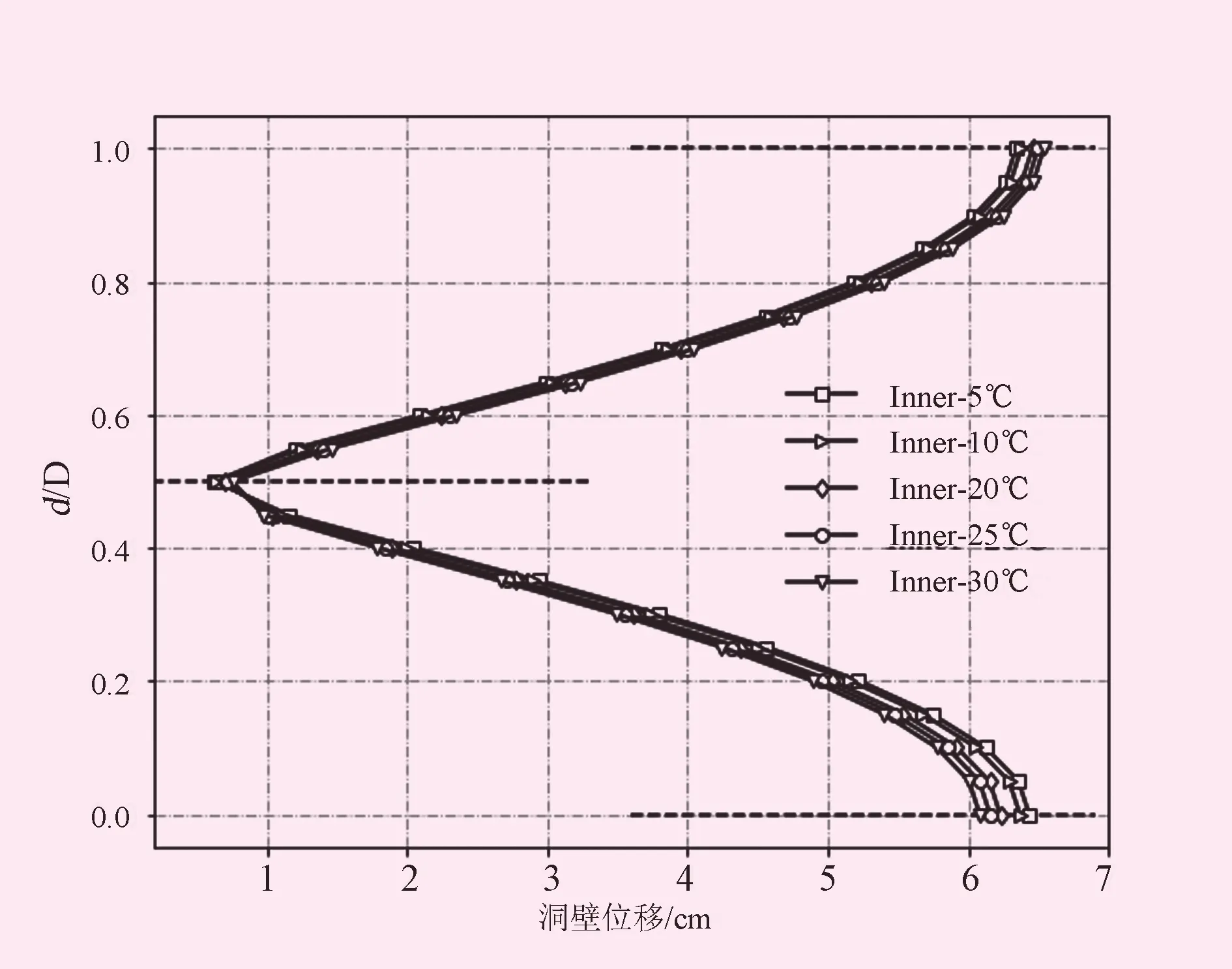
图9 洞壁位移图
相比洞内环境温度变化时的隧洞开挖面位移变化分布情况见图10。由图10可以看出,围岩深部温度的变化会对隧洞开挖面位移产生较大影响,特别是对拱顶及洞底开挖面位移的影响。当围岩深部温度较高时,在隧洞开挖面处引起的位移就越大。洞身洞底及拱顶开挖面处围岩最大位移为8.05 cm,最小位移为0.39 cm,位于侧墙中部以下66 cm处。
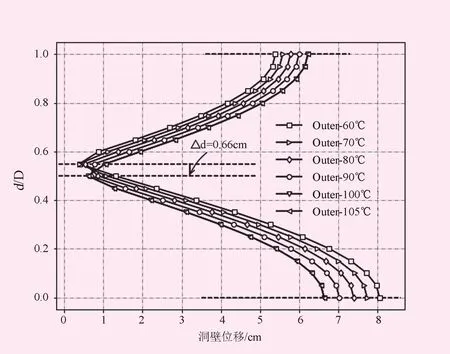
图10 洞壁位移图
3.4 不同地层深度下隧洞周边岩体应力位移分布特征
由图11可以看出,隧洞所处地层深度对边墙中部环向应力的影响特别显著,隧洞埋深越深,环向应力越大。洞壁环向应力最大值位于隧洞边墙中部,且随着隧洞埋深增加,边墙中部的环向应力不断增大;隧洞洞壁环向应力总体上关于隧洞水平轴线上下对称,从拱顶、洞底沿隧洞开挖面到边墙中部,洞壁环向应力非线性递增,在边墙中部达到最大。

图11 洞壁环向应力图
由图12可知,隧洞拱顶位移最大,洞底处次之,边墙中部最小,隧洞埋深在280 m以内时,拱顶及洞底位移关于隧洞水平轴线呈上下对称。当洞身埋深超过280 m时,洞底位移显著大于拱顶位移,不再关于洞身水平轴线对称,边墙中部洞壁位移最小值偏向洞底。

图12 洞壁位移图
3.5 不同侧压力系数下隧洞周边岩体应力位移分布特征
图13、14表明,不同侧压力系数下,洞壁环向应力在边墙处最大,而洞壁位移在边墙处达到最小,洞壁环向应力关于隧洞水平轴线呈上下对称,洞壁位移在侧压力系数较小的情况下,洞壁位移分布基本关于洞身轴线呈上下对称。当侧压力系数为1时,整个隧洞开挖面洞壁各部位环向应力变化不大。
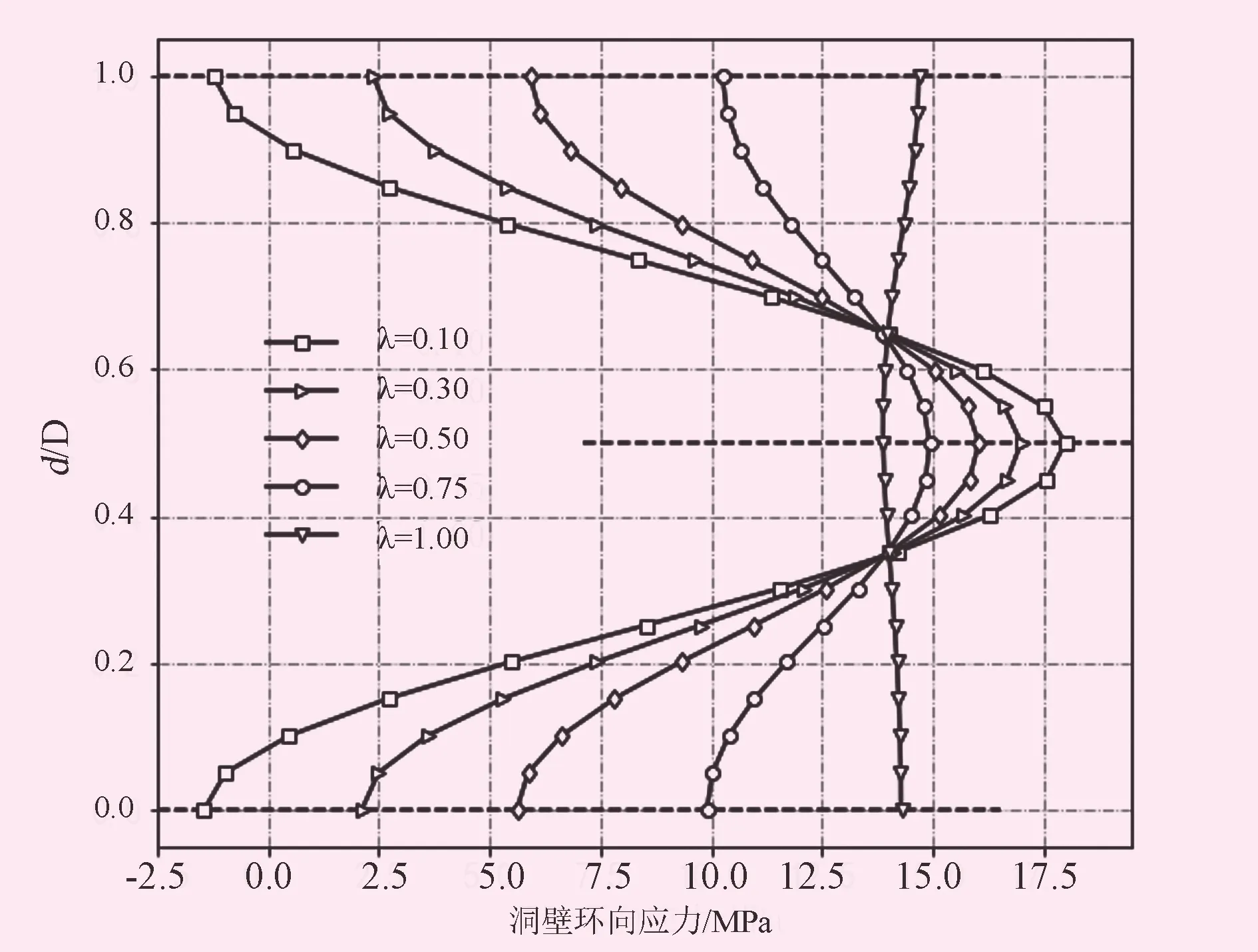
图13 洞壁环向应力图
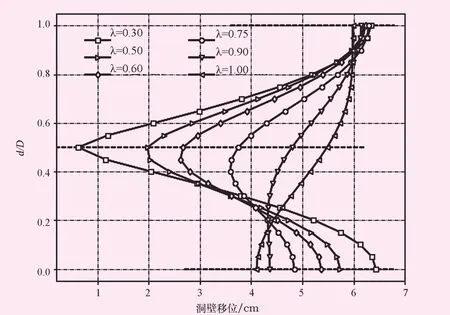
图14 洞壁位移图
4 结 论
本文采用有限元方法,研究分析了水工隧洞在不同温度荷载边界、围岩深度、隧洞埋深、侧压力系数情况下的隧洞围岩应力位移分布情况,得到结论如下:
(1) 隧洞开挖面洞壁处径向应力为0,离洞壁越远,围岩径向应力就越大;同一围岩半径深度处,拱顶径向应力最大,随着离拱顶距离的增加,围岩径向应力不断变小,整个模型径向应力分布关于隧洞水平轴线呈中心对称。
(2) 隧洞开挖后围岩位移关于竖线中心线呈左右对称,最大位移值位于拱顶处,其值为0.06 m,越靠近洞壁,隧洞位移就越大。不同围岩半径处,围岩环向应力不同,洞壁处环向应力最小,离洞壁越远边墙附近围岩环向应力就越小,而拱顶和边墙围岩环向应力就越大,但变化幅度小于边墙处的。
(3) 围岩深部温度的变化会对洞壁位移产生较大影响,特别是对拱顶及洞底位移的影响。隧洞埋深越深,洞壁环向应力越大;拱顶处位移最大,洞底处次之,边墙中部最小。不同侧压力系数下,洞壁环向应力在边墙中部最大,而洞壁位移在边墙处达到最小,洞壁环向应力关于隧洞水平轴线呈上下对称,洞壁位移在侧压力系数较小的情况下,洞壁位移分布基本关于洞身轴线呈上下对称。

