A crossover from Efros–Shklovskii hopping to activated transport in a GaAs two-dimensional hole system at low temperatures
S.Dlimi ,A.El kaaouachi ,L.Limounyand B.A.Hammou
1Physics Department,Faculty of Sciences,Ibn Zohr University,BP 8106,Hay Dakhla,80000 Agadir,Morocco
2Materials and Physicochemistry of the Atmosphere and Climate Group,Faculty of Sciences,Ibn Zohr University,BP 8106,80000 Agadir,Morocco
Abstract:In this paper,we discuss low-temperature hopping-conductivity behavior in the insulating phase,in the absence of a magnetic field.We conduct a theoretical study of the crossover from hopping to activated transport in a GaAs two-dimensional hole system at low temperatures,finding that a crossover takes place from the Efros-Shklovskii variable-range hopping (VRH)regime to an activated regime in this system.This conductivity behavior in p-GaAs quantum wells is qualitatively consistent with the laws laid down in theories of localized electron interactions.Given sufficiently strong interactions,the holes in the localized states are able to hop collectively.
Key words:quantum wells;2D GaAs heterostructues;transport properties;variable range hopping
1.Introduction
At low temperatures,electrical transport in two-dimensional (2D) disordered systems,for which energy states are generally located near the Fermi level,is dominated by the variable-range hopping (VRH) transport mechanism,where the density ofN(E) states is assumed to be constant near the Fermi level[1−6].Based on this mechanism,several studies have confirmed the existence of a Coulomb pseudo-gap in 2D systems,where the density of theN(E) states is linear in the vicinity of the Fermi level,EF,and vanishes atE=EF(N(E)=A(E–EF))[7].This theoretical formalism has been experimentally verified by other researchers[8].
When the temperature is sufficiently low,Mott demonstrated that the resistance between two close neighbors is no higher than the lowest resistance,but that it is necessary to take into account remoter neighbors[9].In the insulating phase,transport can be activated by a similarity in temperature between localized states which are spatially distant but close in terms of energy.
In two dimensions,conductivity can be described by the following equation[1,2,10−12]:
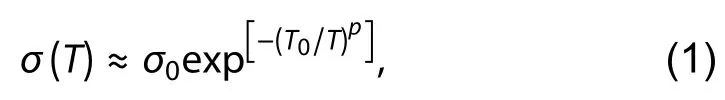
whereσ0is the pre-factor,T0is the charactersitic temperature,p=1/3 for 2D Mott VRH,p=1/2 for Efros–Shklovskii (E–S)VRH,andp=1 for the activated regime.
The pre-exponential factor,σ0,can be either temperature independent[13]or temperature dependent[14,15],based on the type of scattering[16]and the interaction mechanism.
In this paper,we present the behavior of hopping conductivity in a strongly localized state,where the metal–insulator transition (MIT) is approached from the insulating side.
The experimental data which we theoretically analyzed was obtained from a 2D hole gas in GaAs by Hamilton and co-workers[17].The samples had a peak mobility ofμ=2.5 ×105cm2V–1s–1
2.Results and discussion
Fig.1,shows a plot of conductivity dependence on temperature for carrier densities,np,ranging from 3.2 × 1010to 4.4 × 1010cm–2.
The conductivity on the insulating side of the MIT (where dσ/dT>0) varies according to the law represented by Eq.(1),and cannot be interpreted within the transport framework of localized independent electrons.
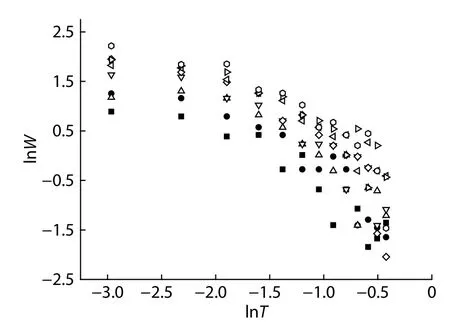
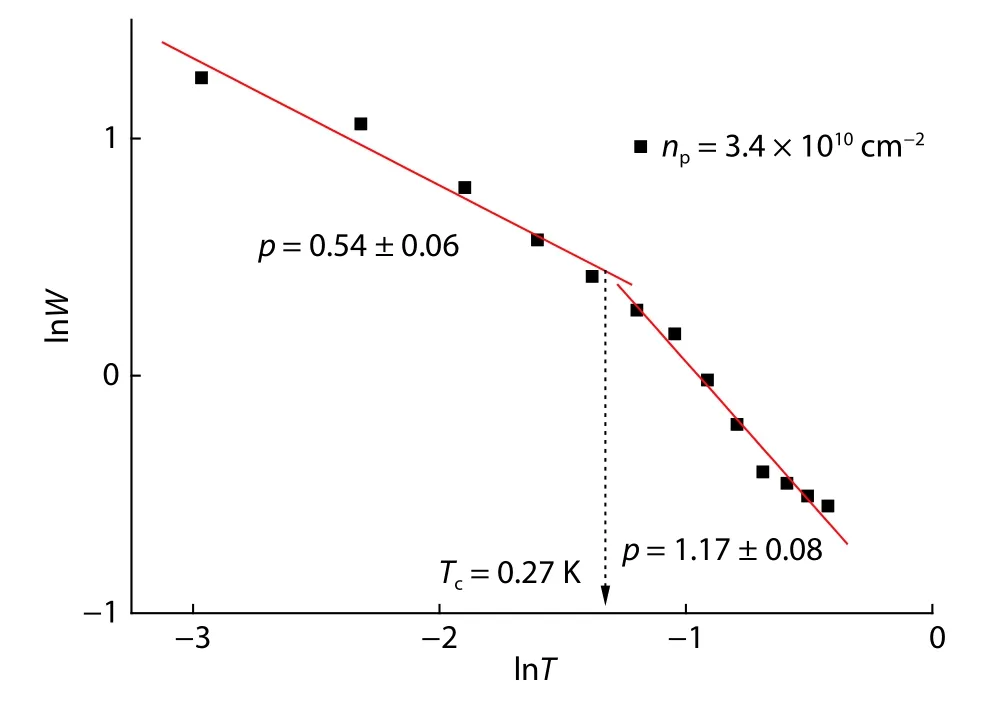
The theory of transport between localized states via VRH gives precise predictions concerning expected temperature dependencies.These theories provide for a temperature-dependent pre-factor according to the power lawσ0However,as this dependence is weaker than the exponential law,one might seek to adjust the conductivity curves as a function of temperature for densitiesnp The most important parameter of this law is the exponentp,which permits the determination of carrier transport mechanisms.Here,we assumed an independent temperature pre-factor,and adjusted the curves,σ(T),based on Eq.(1),withσ0,T0,andpas parameters. Fig.1.Adjustment of conductivity dependence of temperature for 2D p-GaAs system sample for different carrier densities. In Fig.2,we have plotted ln(σ) as a function ofT−1/2,T−1/3,andT–1for different densities.Here,we observe that the data are a close fit for E–S VRH (p=1/2),Mott VRH (p=1/3),and activated hopping (p=1) at temperatures below a critical temperature (Tc=0.27 K);however,we were not able to determine the best exponent,due to the small range of conductivities under examination.To make an exact determination of the dominant transport-regime type in this investigation,we used the resistance-curve derivative-analysis method,(RCDA)[11,18,19]. Using Eq.(1),we can define the logarithmic derivativeW,as follows: This expression can be written in the following form: We can then determine the values of the exponentpfrom the slope: The results are shown in Figs.3 and 4.This approach leads to an exponent,p,which varies with density.Fig.5 summarizes the exponentpobtained at various densities.The standard error for the exponentpis indicated by the error bars in Fig.5. At temperaturesT The activated behavior can be interpreted as the opening of a "hard" gap at the Fermi level,EF,due to a Coulomb interaction,as suggested by Kimet al.[20].In particular,this gap can characterize the formation of a Wigner crystal type of ordered electronic phase,for which a simple activated law can be expected to apply[21].In Fig.6,the activation energy,KBT0,and the characteristic temperatures (TESandTMott) decrease linearly at low temperatures when the density increases,and tend towards zero at a density ofnpc=4.5 ×1010cm–2. Fig.2.ln(σ) as (a) T–1/2,(b) T–1/3 and (c) T–1 of the sample and linear fits where the prefactor σ0is independent on temperature. The activated law can also be ascribed to transport in a percolating system:when a system consists of metal islands separated by insulating zones,the transport of carriers occurs by activated hopping from one island to another.This type of analysis has already been performed in the context of transitions in the quantum Hall-effect regime[22,23],which is now recognized to have percolation transitions[24,25].The percolation model gives a good description of the disorder,but it neglects interactions,which play an essential role in electronic transport.In fact,electron–electron interactions are important in 2D-semiconductor systems,since they can form new phases,such as Wigner crystals,Mott insulators,and excitonic insulators[26,27]. Fig.3.Function lnW versus lnT for various densities. Fig.4.lnW as a function lnT and linear fits for both cases:T Fig.5.The exponent p as a function of carrier densities. When we take into account the correlated hopping between several electrons,the result is a decrease in activation energy,as is the case here.The authors of Refs.[14,28]have shown that the electrons in n-GaAs heterostructures hop collectively,but that the correlations between electrons do not modify the density of states (DOS) calculated for independent electrons (in other words,the DOS remains linear). With regard to the pre-factor,we obtained values of the pre-factorσ01.01e2/h(Forp=1),which is very close to the universal valuee2/hfound in Refs.[29–31].The universal character of the pre-factor in the non-screened regime seems to be due to the interactions between holes,which allows us to envisage a hopping mechanism generated by the interactions between holes.The E–S pre-factorσESwas found to be between 1.23 and 2.16e2/h;however,the Mott pre-factor was found to be equal toσMott2.8e2/h,and independent of both temperature and density.These observations are incompatible with a mechanism where hopping is generated by an electron–phonon interaction,for which a dependence in temperature and density could be expected,and therefore these observations are attributed to a different hopping mechanism,related to the interactions between carriers. For disordered electronic systems at low temperatures,the interaction parameterdefined byis high,the electron–electron collision time is much lower than the electron–phonon collision time,and the hopping mechanism is assisted by electron–electron interactions.In this case,the energy required to make a hop does not come from phonons,but emanates instead from another electron,coupled to the electron making the hop. Our theoretical investigation of the 2D p-GaAs system shows the existence of a crossover from the Efros–Shklovskii variable-range hopping regime (E–S VRH),where a soft gap is created (because the state density is only canceled at a single point,and not at an energy interval),to the activated regime,where a“hard”gap opens at the Fermi level,EF,due to a Coulomb interaction. At lower carrier densities,conductivity dependencies support a law that is simply activated at low temperatures,and which is not supported by localization theories relating to independent electrons.These characteristics are typical of transport in a collective disordered hung phase,but can also be interpreted in the context of a percolating system. Acknowledgements We are grateful to Professor A.R.Hamilton for allowing us to use the experimental results from his dilute 2D GaAs hole system sample.
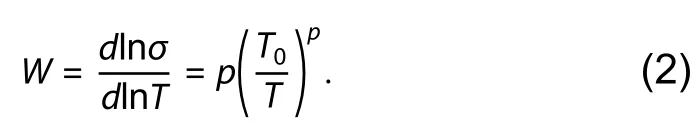




3.Conclusion
 Journal of Semiconductors2021年5期
Journal of Semiconductors2021年5期
- Journal of Semiconductors的其它文章
- WO3 passivation layer-coated nanostructured TiO2:An efficient defect engineered photoelectrode for dye sensitized solar cell
- Compact SPAD pixels with fast and accurate photon counting in the analog domain
- A complete small-signal HBT model including AC current crowding effect
- Facile fabrication of heterostructure with p-BiOCl nanoflakes and n-ZnO thin film for UV photodetectors
- Morphology and crystalline property of an AlN single crystal grown on AlN seed
- Recent progress of physical failure analysis of GaN HEMTs
