大数据思维下的水位流量关系无线推流方法

张英骏，刘林娟

（河北省秦皇岛水文勘测研究中心，河北 秦皇岛066004）

天然河流中的水位流量关系有时呈现单一关系，即稳定的水位流量关系；有时呈现复杂关系，即不稳定的水位流量关系。 受洪水涨落、 断面冲於变化、水草等多种因素影响，任何断面的水位流量呈现稳定单一关系总是相对的，而不稳定则是绝对的。多年来，许多从业人员和学者致力于水位推流的研究，通过引入遗传算法［1，2］、蚁群算法［3］、BP神经网络［4］等数学模型的方法进行优化和提高精度， 也有采用多因素组合影响的水位流量关系的加权模型［5］，对其主要影响因素分别建立处理方案， 按影响因素方案的拟合方差的倒数进行线性加权处理； 在计算机软件开发应用方面， 从严格遵从相关规范的实测流量资料的整编定线［6］，到德国KISTERS公司的水文水环境信息管理系统中的曲线率定模块SKED［7］，无一不是以拟合或生成水位流量关系线为着眼点， 甚至是为了年度资料整编定线而定线，大多是数学模型复杂，实现困难且对不同测流断面的适应性差， 不易实时加入新的测验数据参加分析， 而对那些没有资料整编任务的临时测流断面， 则更谈不上以整编定线成果支持推流作业。

本文探讨一种摆脱一直以来的定线推流的复杂性，而是受大数据思维的启发，用密集的数据替代数学公式的模式［8］，即在收集的尽量多和新的实测水位流量数据的基础上，由计算机直接分析推流。不苛求相对存在的固定线，只依靠绝对散乱的动态点，并能够让使用者感到简单、快捷、灵活、可信。

1 方法

1.1 收集实测数据

通过读取水文数据库得到测流断面历史实测成果数据；遍历本部门各用户得到该测流断面近期实测成果数据；查询获取水情（分）中心实时接收的该断面的最新实测流量报讯信息。上述实测数据构成推流的基础数据包， 需要包含推流主要影响因素相应水位H、实测流量Q、水势Z和施测时间T，正确识别流速仪、ADCP等各种测验方法的测验成果，并能够获取其中的这些信息。对断面受人为影响和严重冲於等变化之前的数据，以及明显测验系统误差的测次，要予以剔除。

1.2 推流分析计算

计算方法是：以推流水位H0为自变量，将数据包内n个测次两两水位（Hi，Hj）和流量（Qi，Qj）直线内插（延长），得到由N=n（n-1）/2个计算流量值组成的序列Qk，由N个计算流量值加权平均获得推流流量Q0。

1.2.1 分配权重

先赋予各影响因素的权值， 再采用模糊相对隶属度赋权法［9］为每个内插流量Qk分配权重Rk。

赋予同推流水位H0最接近的一对实测流量测次最高水位权Hk， 以两个水位同H0差的绝对值之和表示，依次是水位级、水势和施测时间。对断面高中低水进行分级， 一般是认为同水位级具有相同的水流特性，水位同H0处于一个水位级的记0，否则记1，两个测次相加得到水位级权Lk；同样的思路和方法得到水势权Zk； 赋予同当前推流时间T0间隔最近的一对实测流量测次的施测时间最高时间权Tk，以两个时间间隔之和表示，精确到分钟，即最新的实测测次在推流计算中拥有最高的权值。将全部参加分析推流的实测测次两两内插（延长）并取得上述影响因素权后，以Hk，Lk，Zk，Tk的顺序定义排序条件，对序列的N条数据进行升序排序后，逐条赋权值为N，N-1，N-2，…，1，经归一化处理，即分别除以N（N+1）/2得到每个内插流量的权重Rk。显然序列中最大权重和最小权重为别为R1和RN。

1.2.2 制定方案

虽然对各个影响因素和为全部内插数据赋予了不同的权重，但考虑断面水流特性的复杂性，特别是对于断面形状随水位增大有明显突变，或低水有严重水草影响等，使用全部数据进行直线内插无疑是不合理的，还要根据当前水位和水势考虑是否设定只使用同水位级或同涨同落的实测数据，以确保推流结果的科学性。每一次推流都要凭工作人员的经验制定不同的推流方案，这当然需要有足够多的实测流量测次。

1.2.3 输出报告

每次推流计算得到相应水位的流量，根据大断面数据一并解算输出水面宽、断面平均流速等必要的相关信息，形成完整的推流报告，对于缺乏实测大断面资料的临时测流断面，可通过获取最近一次实测流量的水位、起点距、各垂线有效水深等推算建立大断面。

2 实现

2.1 设计思路

为使各项计算可直接借用“四舍六入”数字修约计算函数［10］、时间操作和规范图形比例函数等，以及方便读取大部分的实测流量原始记录和推流结果直接用于推求日平均流量、径流量，将该推流程序作为河流流量测验与成果管理系统（ITMS）的一个组成模块，并共用其数据库管理系统。 将制定推流方案和输出推流结果设计在同一界面完成， 以不作任何筛选的全部实测数据点绘水位流量相关散点图， 并把按方案推流的结果添加到其中供检查对比，如图1。

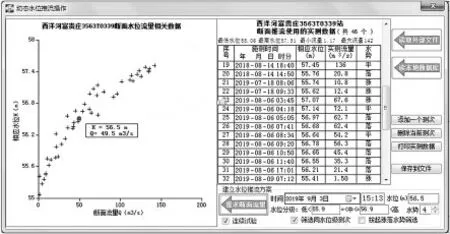
图1 水位流量关系无线推流工作界面

同样运用PB12开发平台的DataWindow的优越特性，实现数据的排序、筛选，以及为权重分配和分析计算提供便利。

2.2 操作设计

实测数据的收集采取外部获取、 本地读取和人工添加共同完成的方式， 自动按施测时间检索识别并过滤重复的测次。 不必按照大数据的法则分段读取分段计算，而是直接在内存中完成，因为一个测流断面的实测测次数量，即便是经过两两组合后也不会形成真正意义上的“大”数据。不排除存在收集到的实测数据信息不完整而影响推流的实施，例如某测次的测验人员丢掉了水势，甚至临时断面实测流量记录中缺少相应水位，这只能由人工来弥补完善，一般可剔除这类不可信的测次，体现该推流模式是灵活的。

每次推流完成后， 应将使用的实测数据以文件的形式保存，下次直接调取并添加新的实测测次，使生成的推流数据序列始终保持生命力， 这对于传统的定线推流是难以做到的。

3 评价

3.1 接受检验

虽然该方法得到的结果是点中点， 而不是线中点， 但这并不妨碍使用流量资料整编的方法进行检验。 以西洋河富贵庄站2年计46次实测流量数据推流为例，假定从水位55.10m至57.90m以步长0.10m各推流计算1次，得到29次推流流量，如图2，就形成了一条水位流量关系曲线。

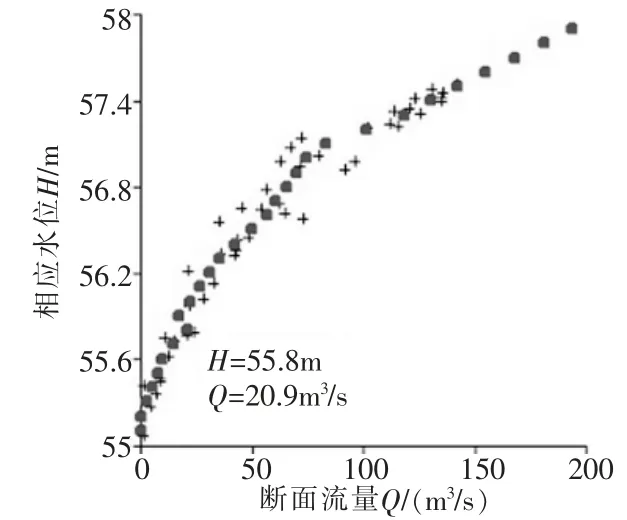
图2 推流计算形成的水位流量关系曲线

考虑该断面形状较复杂， 水位55.9以下是由2条沟渠组成的复合断面且汛期水草密集，水位55.9m以上出现滩地且有植树和农作物。 依此设定高、中、低3个水位级，落入其中点子的数量分别为：高水17个，中水19个，低水10个。 推流时勾选“筛选同水位级测次”进行分析计算，因实测测次偏少，不再考虑区分水势为同涨同落。

目测图形可以看到，低水段同中水段趋势明显不同，中水段同高水段不太突出。 通过对此计算形成的水位流量关系曲线按高、中、低水分段做偏离数值检验和t学生氏检验均得到可接受的、令人满意的结果。

3.2 误差分析

3.2.1 同定线推流对比

定线推流的原则是通过点群中心定出一条平滑的关系曲线，这样可以消除一部分测验误差［11］，而在这里是在点群中心找到一个点作为推流结果，更有利于消除测验误差，但这些点连在一起显然不是平滑曲线，是完全依赖实测数据趋势的曲线，且会随着实测数据的增减而动态变化，尽管同整编要求相悖，但这是该方法的特点和优点。

3.2.2 处理突出点

为防止由测验系统误差带来的推流系统误差，需在程序提示下人为对突出点进行处理。任何特殊原因造成的某测次甚至多个测次出现较大偏离，都会较大影响一般情况下断面推流的精度， 因为对n个实测点中的1个测次将有n-1个内插结果参与计算，势必产生较大的影响权重。 事实上，通过程序调试功能查看两两内插结果可发现，由突出点参与的内插结果已经失去意义，甚至向下延长的情况会出现流量为负数。

3.3 运行效率

通过在普通配置水平的计算机上试验， 对不设筛选条件的122个测次进行测试性推流，完成其两两组合7381次内插计算和排序分配权重完成加权计算输出结果，仅需13s时间。

4 结语

这种以积累越来越多的实测数据做支撑，每次推流都由计算机进行较大强度的运算得到推流结果的方式，操作简单快捷。 测验规范要求的严密性和测验手段的先进性，大大提高了测验结果的可信性，更为推流结果的可靠性提供了保障。通过多个测流断面在水情服务方面的实际应用看，相比传统的定线推流有着更大优势， 且更为目前众多水文基层测报人员接受。 与其说该方式同流量资料整编要求脱节，不如说这是行业上流量资料整编业务的一点创新，是推动水文基层业务工作现代化、信息化的具体尝试。

但从文中使用的方法和考虑的影响因素等可发现，这种方法大多是机械性运算，甚至只能凭测报人员的经验，虽实用但缺乏充分的理论依据，因此需要进一步完善。