有关装量差异验证方法的讨论
(无锡药明偶联生物技术有限公司,江苏 无锡 214000)
在注射剂的生产过程中,需要控制每一瓶的装量差异。例如在无菌冻干粉针的生产过程中,需对每一瓶的液体装量差异进行控制。从而保障冻干后的成品制剂与标示量的差异在一定的范围之内。按照一般的要求,装量应在标示量的95%~105%之间[1],有些药品甚至要求会更严一点。
下面就以无菌冻干粉针的生产过程中,液体装量差异作为案例进行讨论,如何用科学的方法验证装量差异。
1 方法分析
1.1 传统的验证方法
在装量差异的传统验证方法中,以无菌冻干粉针为例。由于其成品必须在标示量的95%~105%之间,在料液浓度的中间体含量出来以后,就会确定一个装量差异的范围。为了确保装量在标示量的95%~105%,因此需要一个更为严格的内控指标。如果产品质量标准规定的范围为±5%,那生产过程的内控标准就应该小于这个值,通常定为≤±4.5%,甚至范围更窄。
在生产过程中利用抽样检测的方法来确定装量差异,是否符合上述规定范围的要求。表面上看这样的做法是一个比较严谨的做法,而且其要求也是比较严格的。但实际上这个方法非常模糊,看到的仅是抽取到的样品情况。没有对潜在的不良率进行预判和评估。有可能不良品出现时候并没有被检测到,而在放行检验阶段被发现。
为了减少上述风险的产生,在进行装量差异验证时,范围要求更为严格,这一做法会给验证带来难度,同时也无法判断该严格要求是否能符合实际情况。
以无菌冻干粉针的控制装量差异为例,装量的差异并不会随验证范围标准收紧而改变,它是由该工序的质量特性所决定的。工序的质量特性由设备固有能力所决定,如果灌装时所使用设备是蠕动泵,那它与如下的因素有关:
(1)蠕动泵转速的控制精度和稳定性;
(2)乳胶管的粗细、壁厚和材料的弹性;
(3)目标控制点位置的设置(这是在实际操作过程中唯一可随时修正的参数)
灌装设备并不能随着装量差异范围的改变而进行调节。因此在收紧范围标准的时候,设备实际的性能情况并不会发生改变,因此只能单一地判断该范围内的数据是否能够满足要求,从而进行判断或者评估在实际的生产过程中是否能够满足质量要求。但是如果更换一种统计学的方法,只需要通过对抽样数据的计算,就能够从统计学角度获得各个标准范围时可能出现的不良率,能更科学有效且便捷地对设备性能进行一个判断,这个方法就是利用工序能力指数来进行判断。
1.2 工序能力和工序能力指数
1.2.1 准确度Ca(Capability of Accuracy)
实际中心与规格中心的差异称为准确度,Ca仅适用于双边规格,单边规格无法计算Ca。其计算公式为:

式中——平均数;
μ——规格中心;
USL——规格上限;
LSL——规格下限;
T——USL-LSL。
1.2.2 精确度Cp(Capability of Precision)
表示品质特性的散布范围大小或集中程度称为精确度,即质量能力,CP越大则表示其质量能力就越强。
双边规格计算公式:

仅定规格上限或下限的计算公式:
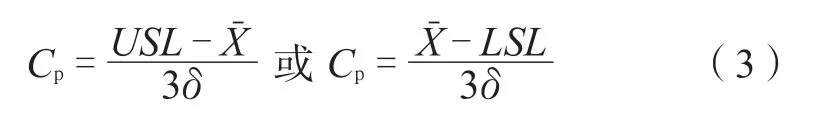
式中——平均数;
δ——标准差;
T——USL-LSL;
P——加工宽度(±3δ 休哈特原则)。
1.2.3 工序能力指数Cpk(Complex Process Capability index)
是指工序在控制状态下,工序符合规格的能力。是过程的“质量能力”与“管理能力”二者的综合结果。
双边规格计算公式:

仅定规格上限或下限的计算公式:

式中——平均数;
δ——标准差;
USL——规格上限;
LSL——规格下限。
CP与中心无关,即它没有上限和下限。CPk有上限和下限,在仅有单侧值时侯CP=CPk。CP是永远大于、或者至少等于CPk的,CPk是不会小于零的。另外,CPk与不良率还存在表1中的对应关系[2]。
对于Cpk来说≤0.67 为严重不足,0.67~1 为不足,1~1.33 为尚可,1.33~1.67 为充分,≥1.67 为过剩,一般来说对于制程的Cpk达到1.33 即可,药品是一个特殊的商品,因此要求制程的Cpk需要尽量达到1.67以上。
由表1中的数据可以看出,不同的Cpk对应着不同的不良率数据。也就是说可以根据抽样的数据进行计算,获得统计学中潜在可能的不良率[3-5]。
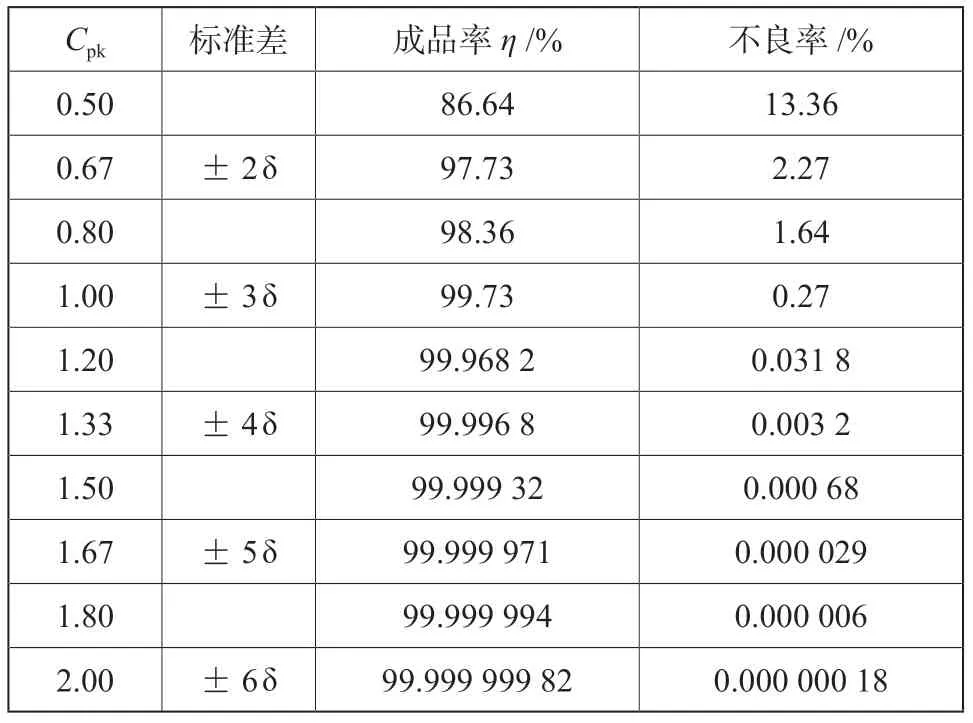
表1 Cpk 与工艺不良率的关系Tab.1 The relationship between Cpk and process defect rate
2 用实际工序能力指数Cpk 作为验证判断的依据
在一个批次无菌冻干生产的灌装中,现场抽取了100 个样品对其检查装量,将测得的装量数据汇总于表2中。
如果质量标准要求的标示量范围为±5%,那就将灌装时的差异范围定义为≤±4%。用工序能力指数的方法根据表2的数据,计算得到其Cpk为3.75,其控制图见图1所示。从表1中可以查到其对应的不良率远小于0.000 000 18%,其USL为2.08,LSL为1.92,4δ 在其界限之内且结果远优于要求的范围。
如果将灌装时的差异范围定义为≤±2%,同样根据表2的数据,计算得到其Cpk为1.85,其控制图见图2所示。从表1中可以查到其对应的不良率远小于0.000 006%,这个结果仍在可接受的范围之内,但这个时候4δ 已经相对来说接近USL和LSL了,也就是说可能已经到了可接受标准的边缘了。
再进一步将灌装时的差异范围定义为≤±1%的情况,同样根据表2的数据,计算得到其Cpk为0.89。其控制图见图3所示,控制限已经超出了4δ 的范围。从表1中可以查到其对应的不良率大概为1.7%,这个结果已经超出了接受标准。在控制图上所示4δ 已经超出了USL和LSL的界限。
将不同要求范围情况下对应的工序能力指数都计算出来见表3所示[4-5]。
在表3中能够清晰地显示设备的能力能够支持到哪个范围,免去了用传统验证一次次盲目的试验。从表3中的数据可以看到,装量差异要求≤±1.5%已经不合适了,实际设备性能的界面在±1.5%~±2%之间。但如果装量的目标值发生变化,这个界面的位置也是可能发生变化的。再有关联因素的变化,也会影响到这个界面的变化。

表2 一个批次无菌冻干粉针料液装量数据Tab.2 A batch of aseptic freeze-dried powder injection liquid filling data

图1 要求范围在±4%时装量的控制图Fig.1 A control chart with a required range of ±4% of the load
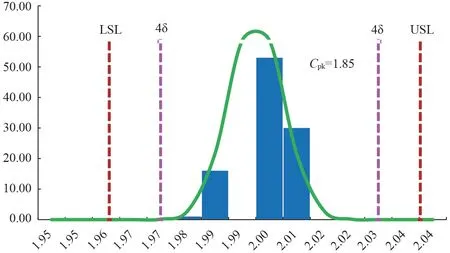
图2 要求范围在±2%时装量的控制图Fig.2 A control chart with a required range of ±2% of the load
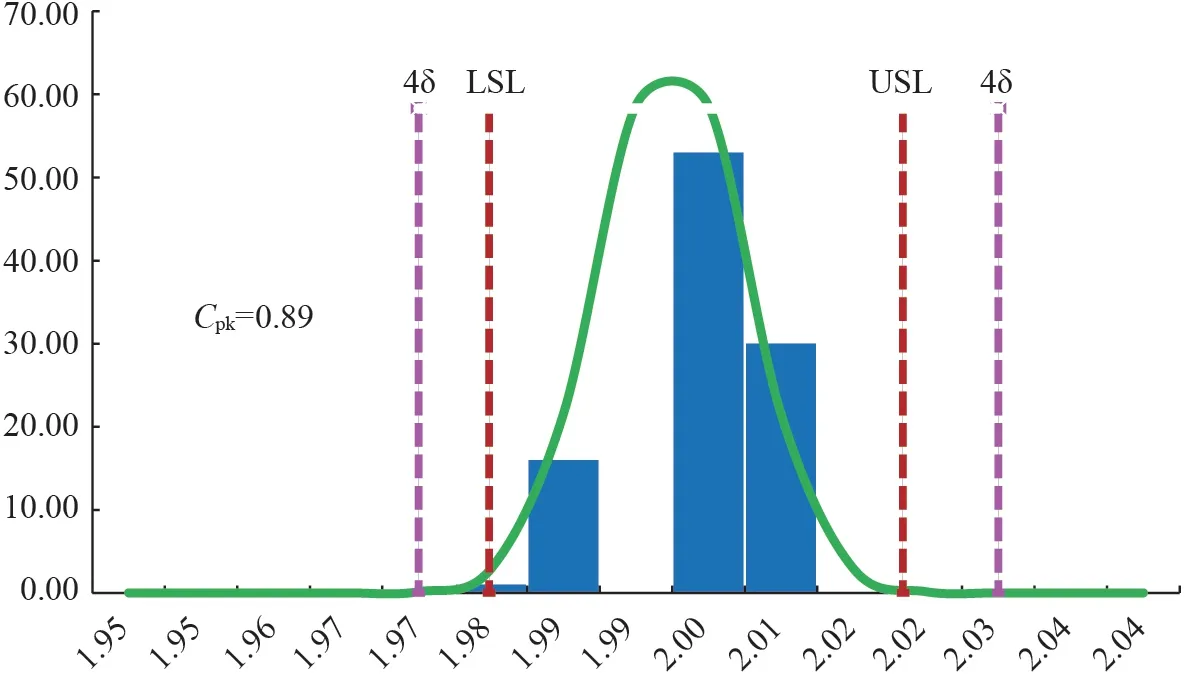
图3 要求范围在±1%时装量的控制图Fig.3 A control chart with a required range of ±1% of the load

表3 固定配置下的装量控制能力Tab.3 Capacity control under fixed configuration
但对于传统验证而言,100 个验证数据尚有不足,不能充分地反应出设备性能的好坏,这需要加大人力,物力进行更大批次的验证。与此同时就该批数据而言,若验证的要求即使为±1%,也是全部符合的,但是利用工序能力指数的方法进行计算,±1%这个产生不良品的概率是不可接受的,所以传统验证方法所得到的数据只能对数据本身进行一个判定,而不能对其潜在风险进行一个指导,故传统验证不一定能真正地反映出该设备现有的真实情况,是存在潜在风险的。在传统验证中通常利用水等替代物代替药液进行装量差异的验证,这本身就给设备增添了一定量的误差。
同时如果想要知道设备的极限,或要进行一些报警参数的确定时,设备的极限性能就会被需要,那依据传统验证每一种规格或者每一种装量都需要将各个范围重新进行确认,这大大增加了人力与物力的投入。
因此利用工序能力指数的方法来对制成能力进行判断是更科学有效且快捷的。
当然用工序能力指数来计算制成能力的时候,是基于数据正态分布的情况下。实际上质量特性的数据有80%是符合正态分布的,不满足正态分布条件的数据,即使计算Cpk也不会得出满意的结果。所以不必要先纠结抓取数据是否符合正态分布。
3 结论
综上所述,可以看到用Cpk的统计学方法,只需要在生产过程中随机地进行一次取样,就能够获得不同要求范围的工序能力指数和不良品率数据。不仅可以大幅度地减少验证的工作量,还能够评估出现不良率的概率风险。这样的方法比用替代物料做装量差异验证合理,而且不会影响实际的生产活动。
在实际的应用中,甚至可以对每批的抽样数据进行计算,通过Cpk的数据变化还可以判断蠕动泵的乳胶管是否需要更换了,如果更加精准一点还可以将数据针对某一个灌装头来进行判断。
用工序能力指数Cpk来作为验证装量差异的工具,它还能够给出不良品出现的概率,进一步判断制程是否存在风险。只需要在平时利用真实的生产数据,通过计算得出验证的结果,并不需要专门去开设一些利用替代物料进行的验证项目。

