面向星载激光光斑的质心定位精度分析

朱红，谢俊峰，孙广通，刘小阳，么嘉棋

(1.防灾科技学院 生态环境学院，河北 廊坊 065201；2.自然资源部国土卫星遥感应用中心，北京 100048；3.山东科技大学 测绘科学与工程学院，山东 青岛 266590)

0 引言

质心定位精度是监视激光质心位置变化的前提与基础，是决定星载激光测高仪定姿精度的关键因素之一，也是探测卫星平台颤振规律的一种新方法[1-2]。因此，质心定位精度对激光测高数据的处理具有一定理论意义与参考价值[3-4]。ICESat卫星平台所搭载的对地观测激光测高系统(geoscience laser altimeter system，GLAS)可以捕获激光光斑数据，能够准确地获取激光指向信息与激光状态信息，被应用于冰原地形的测量、大气特性与植被信息的提取等[5-6]。

目前，根据质心定位精度可以将现有的研究方法分为2类：传统的质心定位方法、兼顾空间分辨率提升的细分定位方法[7-9]。基于传统的质心定位方法主要包括灰度加权[10]、高斯曲面拟合[11]、椭圆拟合[12]等。其中，灰度加权方法主要考虑的是像素值与权重的关系，对激光光斑的对称性要求较高；高斯曲面拟合法是通过高斯函数模拟成像过程的点扩散函数，从而对激光光斑进行定位，具有较好的稳定性；椭圆拟合法是将激光光斑视为椭圆，在形态学提取边缘点的基础上进行最小二乘拟合，从而对光斑质心进行定位。

在图像识别过程中，当固有的图像空间分辨率较低时，会导致提取的特征产生不可忽略的误差。为解决这类问题，专家学者提出了兼顾空间分辨率提升的细分定位方法，主要是引入图像超分辨率重建技术[13]，提升激光光斑图像空间分辨率，解决因分辨率过低导致定位精度难以提升的问题。目前，超分辨率重建方法较为成熟，包括传统方法的插值法[14-15]、反投影迭代法[16]、凸集投影法[17]、最大后验概率方法[18]以及基于深度学习的超分辨重建方法[19-20]等。但是，基于图像超分辨率重建方法的星载激光光斑质心定位的研究相对较少，文献[13]通过稀疏表示的方法提高星图的空间分辨率，提高了星图质心的定位精度。可见，将超分辨率重建方法应用于星载激光光斑质心定位的研究中具有一定的可行性。

综上所述，本文结合GLAS激光光斑图像空间分辨率较低、光斑形状随激光器能量衰减、成像方式及卫星平台颤振引入噪声信息等自身特点，将不同质心定位方法应用于GLAS激光光斑图像，对比分析不同质心定位方法的精度。相关实验结论可为后续国产卫星激光测高仪足印影像的处理提供参考。

1 质心定位原理

为验证不同质心定位方法应用于GLAS激光光斑定位的可靠性，本文选取具有代表性的灰度加权、高斯曲面拟合、椭圆拟合以及超分辨率重建技术等方法，通过多种方法对激光光斑质心定位精度的影响进行分析。

1.1 基于质心跟踪的灰度加权定位方法

传统的灰度加权法是将激光光斑作为基元分别对每个光斑进行质心定位，不仅容易受到背景噪声的干扰，而且长时序GLAS激光光斑中存在最大能量值不唯一的情况，将影响激光光斑质心定位精度。因此，本文对传统灰度加权方法进行改进，通过质心跟踪约束提高灰度加权质心定位方法的可靠性，如图1所示。

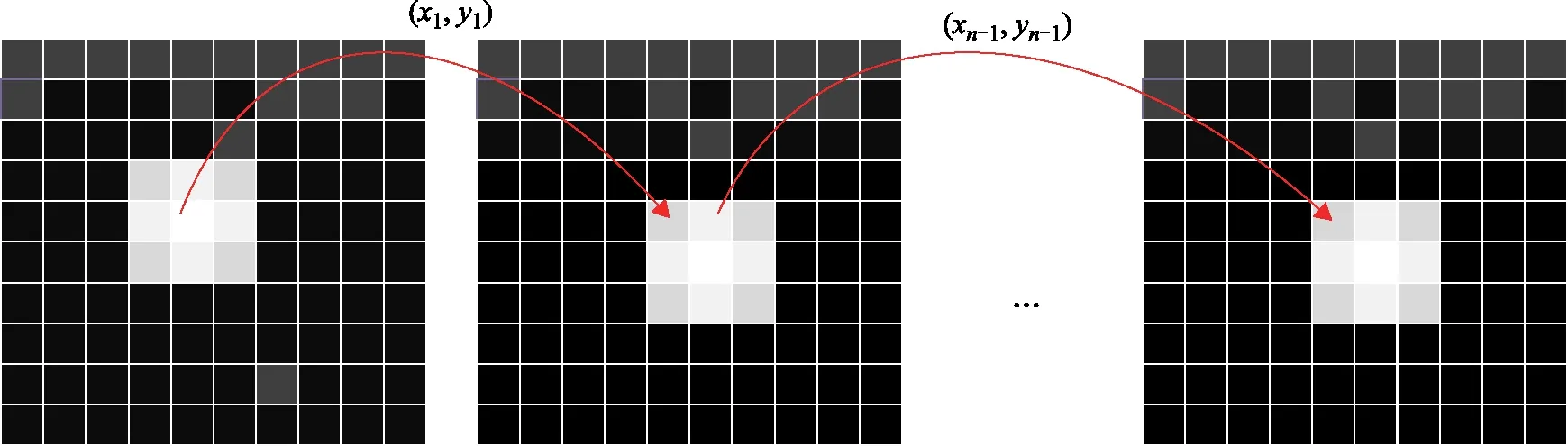
图1 质心跟踪的灰度加权方法

首先，确定激光光斑中能量最大值所对应的坐标位置；其次，以最大值为中心建立自适应窗口；最后，利用灰度加权法提取光斑质心坐标。在长时序激光光斑质心提取过程中，通过前一个质心坐标位置约束下一个激光光斑质心坐标。其中，灰度加权质心定位的数学描述如式(1)所示。

(1)

1.2 高斯曲面拟合的质心定位方法

高斯曲面拟合法是基于二维高斯分布规律提取目标的质心坐标，按照高斯曲面规律变化，其投影中心所在像素的灰度值最高，周围像素灰度值递减，通过高斯曲面拟合数字化的目标图像，从而确定目标质心所在位置。假设光斑的灰度分布符合以映射坐标(xk，yk)为中心的二维高斯分布，则像素(xi，yj)的灰度值f(xi，yi)的计算如式(2)所示。

(2)

式中：(xk，yk)为光斑的质心坐标；参数A为激光光斑的总能量；δ为二维高斯分布的均方差。δ与散焦程度和像差大小的综合效果有关，对式(2)两边同时取对数得到式(3)。

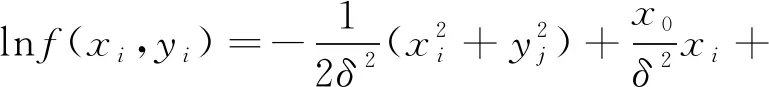
(3)

(4)

进而通过最小二乘方法求得激光光斑质心坐标，如式(5)所示。

(5)

1.3 基于椭圆拟合的质心定位方法

当目标成像区域近似椭圆形时，可以采用椭圆拟合法提取光斑质心坐标。该方法较为简单，但光斑强度不对称时会造成较为严重的定位误差。一般采用二次曲线拟合方法提取目标区域边缘，对边缘坐标进行椭圆拟合，将拟合椭圆的中心作为目标质心坐标。椭圆的一般数学表达如式(6)所示。

ax2+bxy+cy2+dx+ey+f=0

(6)

通过最小二乘原理求出参数a、b、c、d、e、f的最优解，得到椭圆的一般方程。利用得到的最优解计算光斑质心坐标，质心的数学表达如式(7)所示。

(7)

1.4 基于超分辨率重建的质心定位方法

与传统质心定位方法不同，本文顾及激光光斑固有空间分辨率的提升，将超分辨率重建方法引入到激光光斑质心定位中，分析其对激光光斑质心定位的影响。利用最大后验概率方法[18]对窗口内的光斑进行局部超分辨率重建，对光斑质心进行高精度亚像素级定位。假设IL为原始激光光斑，在已知激光光斑信息的条件下，估算出最优的高分辨率激光光斑能量分布IH。依据贝叶斯理论，最大后验概率的数学表达如式(8)所示。

(8)

式中：P(IH)与P(IL)分别代表高分辨率激光光斑IH与低分辨率激光光斑IL的先验概率；P(IL/IH)代表当高分辨率激光光斑为IH时，对应的低分辨率激光光斑IL的条件概率。根据贝叶斯理论，由于IL是已知的，P(IL)可以被视为常数，对于求解高分辨率激光光斑IH无关，可以被忽略，将式(8)改写为式(9)。

(9)

对式(9)取对数得到式(10)。

(10)

基于最大后验概率估计的超分辨率重建模型中，先验概率模型P(IH)采用高斯分布函数，条件概率P(IL/IH)转化为待求高分辨率激光光斑与低分辨率激光光斑相同来求解。

在超分辨率重建的基础上，利用灰度加权方法对激光光斑进行亚像素级质心定位。将超分辨率重建后的光斑质心坐标分为像素级与亚像素级2个部分。像素级定位是确定光斑中心所在的像素级坐标，即计算激光光斑能量的最大值，数学表达如式(11)所示。

(xpixel，ypixel)=max{Ew(i，j)}

(11)

式中：(xpixel，ypixel)为激光光斑的像素级坐标；Ew(i，j)为窗口w内像素坐标(i，j)对应的能量值。

通过超分辨率重建方法提升激光光斑的分辨率，对激光光斑进行高精度亚像素级定位。利用灰度加权提取重建后的光斑质心坐标，对重建窗口内的质心进行亚像素定位。基于超分辨率重建质心定位的计算方法如式(12)所示。

(12)

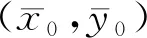
2 实验分析

本文主要研究GLAS卫星平台上LPA所记录的激光光斑图像，图像大小为20像素×20像素，图像灰度值范围为0～255，其中激光光斑散布在几个像元中，大小一般不超过5像素×5像素。实验随机选取2轨GLAS04级激光光斑图像，每轨数据包含463 920景激光光斑图像，采集时间分别为2015年6月17日与2015年10月26日，其中部分激光光斑图像如图2所示。从激光光斑图像可以直观看出，激光光斑图像空间分辨率较低，光斑形状随激光器能量衰减，属于非标准的高斯分布，并存在一定的噪声信息。

实验过程中将质心跟踪灰度加权、高斯曲面拟合、椭圆拟合及超分辨率重建质心定位方法应用于GLAS激光光斑数据的质心提取。实验中，2115-0279轨激光光斑数据采集时间为2015年6月17日，2117-1293轨激光光斑数据采集时间为2015年10月26日，实验结果如图3、图4所示。x轴为激光光斑图像景数，y轴为质心定位坐标，单位为像素。

图2 激光光斑数据

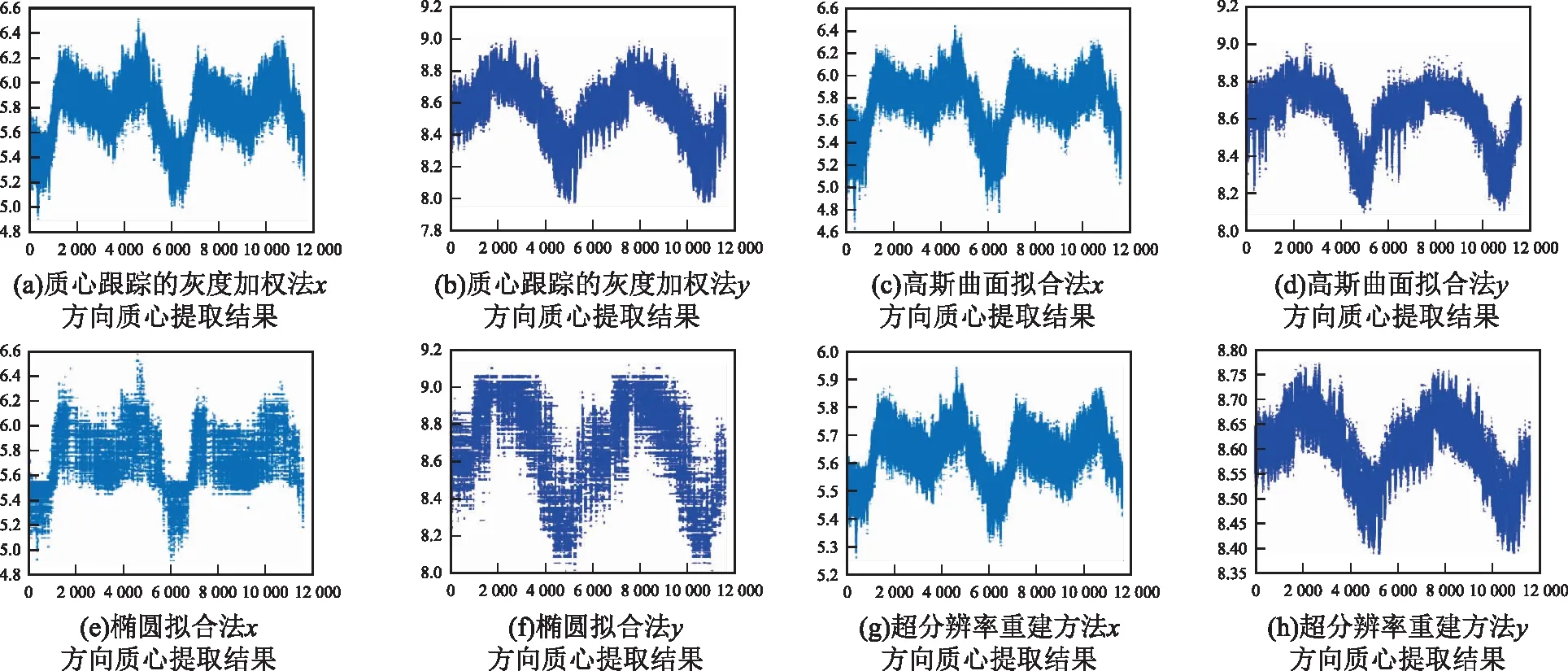
图3 2115-0279轨质心提取结果

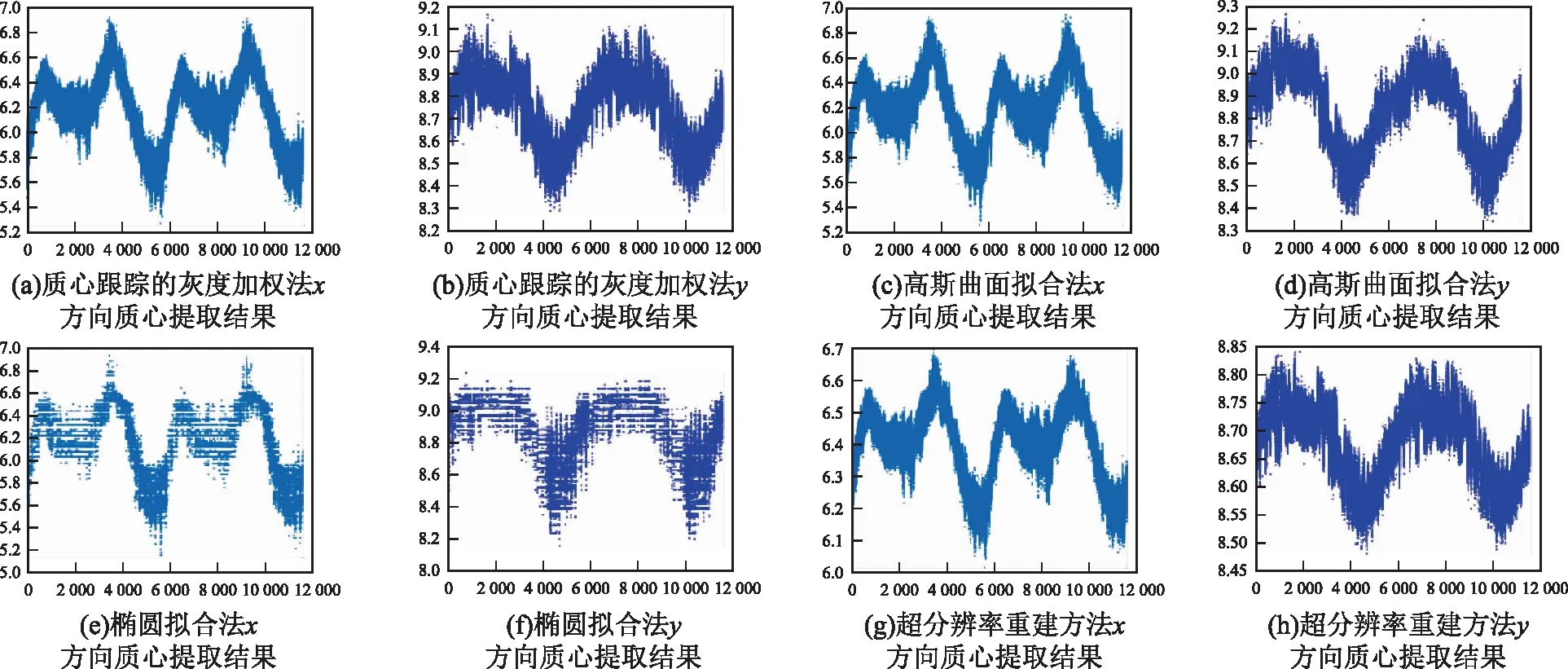
图4 2117-1293轨质心提取结果

从图3、图4中可以看出，随机选取的激光光斑质心定位结果在x与y方向均呈现周期性变化，这也反映出卫星平台在轨运行时存在颤振现象。基于长时序激光光斑质心在x与y方向的变化规律，拟合得出激光光斑质心在x与y方向均存在周期约为1.6 h的姿态变化，即探测到卫星平台颤振周期约为1.6 h。为了定性分析不同质心定位方法的精度，实验通过傅里叶函数对4种不同质心定位方法的质心轨迹进行拟合，计算激光光斑质心与拟合函数的残差，实验结果如表1所示。

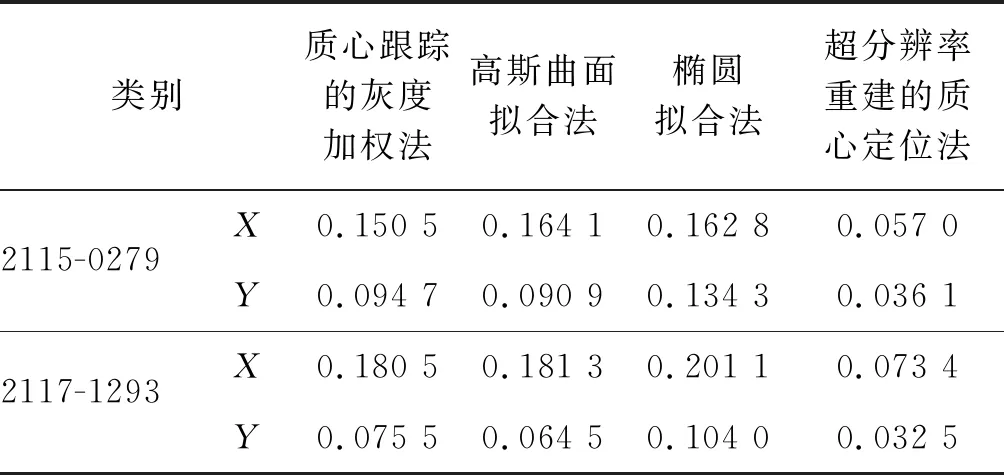
表1 质心定位精度对比结果

从表1可以直观地看出，质心定位精度由高到低分别为超分辨率重建的质心定位法、质心跟踪的灰度加权法、高斯曲面拟合法以及椭圆拟合法。实验同时记录了不同质心定位方法的耗时情况。质心跟踪的灰度加权法平均耗时约为0.013 s，高斯曲面拟合法平均耗时约为0.020 s，椭圆拟合法平均耗时约为0.042 s，超分辨率重建的质心定位方法平均耗时约为0.026 s。

3 结束语

本文以GLAS04级产品记录激光光斑图像作为实验数据，结合激光光斑图像的自身特点，通过多种方法分析影响激光光斑质心定位的因素，并对不同的质心定位方法进行对比分析，同时统计质心随时间的变化规律，进而探测卫星平台的颤振规律，结论如下。

1)不同质心定位方法应用于GLAS激光光斑图像，质心定位精度的高低分别为超分辨率重建的质心定位法、质心跟踪的灰度加权法、高斯曲面拟合法以及椭圆拟合法。质心定位法所需的时间长短分别为椭圆拟合法、超分辨率重建的质心定位法、高斯曲面拟合法、质心跟踪的灰度加权法。

2)不同质心定位方法均可以间接探测到卫星平台存在周期约为1.6 h的姿态变化规律。通过监视卫星在轨激光光斑质心变化规律，可提高激光的指向角精度，最终提升激光定位精度。