生物光声层析成像中超声探测器特性对图像质量的影响及解决方法

孙 正 孙慧峰

1(华北电力大学电子与通信工程系,河北保定 071003)

2(华北电力大学河北省电力物联网技术重点实验室,河北保定 071003)

引言

光声层析成像(photoacoustic tomography,PAT)是一种具有高光学对比度和高空间分辨率的新型复合生物医学成像方法[1-3]。该方法采用短脉冲激光照射生物组织,组织吸收激光能量后,由于瞬态热弹性膨胀激发出宽带超声波(即光声信号)并向组织表面传播,超声换能器采集光声信号后送入计算机中,采用适当的图像重建算法通过求解逆问题重构出组织的初始声压分布图或光吸收能量分布图。

在理想条件下,例如组织具有恒定的声速和密度、不考虑超声波在组织界面处的反射和散射、超声探测器为具有全向响应(即对来自任何方向的压力波都同样敏感)的理想点探测器、忽略探测器的空间脉冲响应(spatial impulse response,SIR)和电脉冲响应(electrical impulse response,EIR)、所采集的光声信号数据集是完备的等,采用解析法[4-8]和迭代法[9-12]可以重建出高质量的图像。然而在实际应用中,由于点探测器的有效面积小,导致采集信号的信噪比较低,且检测到的声压信号并非组织产生的原始信号,而是探测器的脉冲响应和原始信号作用后的结果。此时,若在理想假设前提下重建图像,则会导致图像质量的下降。在介绍超声探测器特性对PAT 成像质量影响的基础上,文中对忽略超声探测器特性造成的重建图像质量下降问题的解决方法进行总结和归纳。

1 超声探测器特性对光声成像质量的影响

超声探测器的特性对光声图像重建质量的影响主要体现在以下6 个方面。

1)有限孔径效应。大部分光声图像重建算法都是基于理想点探测器的,但是点探测器的有效面积小,信噪比低,灵敏度差,不能检测出微弱信号。在实际应用中,通常采用探测面积较大的非聚焦平面超声换能器解决信噪比低的问题。但是探测器的SIR(即衍射效应)会影响其接收角度和信号延迟精度,导致有限孔径效应[13],即在给定的探测器带宽下,当目标远离探测器圆形扫描轨迹中心或者靠近探测器表面时,成像的切向分辨率会下降。

2)SIR 和EIR。处于接收模式的超声换能器采集的声压信号是组织产生的初始声压与探测器的SIR 和EIR 卷积后的结果。如果在图像重建中忽略换能器的EIR 和SIR,会导致重建图像的空间分辨率降低,并出现伪影和失真[14]。

3)方向性。探测器的尺寸有限,不具有全向响应,而是对来自某一特定方向的入射波表现出较高的灵敏度,对于另一些角度的压力波则不敏感,进而导致重建图像中出现伪影[15]。

4)扫描半径。对于采用多个换能器进行数据采集的圆形或环形扫描PAT 系统,很难将所有换能器都精确地放置在与扫描中心距离相同的位置上。当采用反投影算法重建图像时,需要输入每个换能器的扫描半径,如果对所有换能器使用相同的扫描半径,则会导致图像失真。

5)有限的探测角度和频带宽度。对于采用线性超声换能器阵列的PAT 系统(例如手持式PAT系统),平面检测方式有助于在身体表面进行灵活定位,但其探测角度和带宽是有限的,导致重建图像中存在有限视角伪影和有限带宽伪影。其中有限视角伪影表现为在图像中沿成像目标两侧延伸的弯曲条纹状伪影。探测器的有限带宽导致其在采集光声信号时滤除了信号中的高频和低频成分,使得图像中实体目标的内部呈现空心特征,即有限带宽伪影,此外有限带宽也限制了成像的轴向分辨率。

6)位置的不确定性。在基于模型的光声图像重建方法中,超声探测器位置的不确定性会导致建模误差,且误差随不确定性程度的增加和探测器数量的减少而增大。

2 有限孔径效应的解决方法

目前,解决超声探测器有限孔径效应的方法主要有采用聚焦超声换能器的方法、采用负折射率透镜的方法、基于模型的图像重建方法和压缩感知(compressed sensing,CS)法,如表1所示。

表1 解决超声探测器有限孔径效应的主要方法比较Tab.1 Comparison of methods for solving the finite aperture effect of the ultrasonic detector

2.1 聚焦超声换能器

与理想点探测器不同,聚焦超声换能器的光声辐射场具有一定的角度范围,可在该范围内使用聚焦换能器的焦点(即虚拟点探测器)检测组织产生的光声信号,如图1所示。无损介质中光声信号的产生和传播满足光声波动方程为

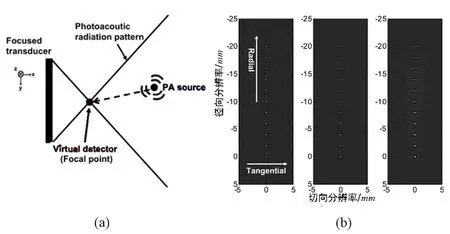
图1 虚拟点探测器示意图及仿真光声图像重建结果。(a)虚拟点探测器示意；(b)分别采用点探测器、非聚焦换能器和聚焦换能器时重建的光声图像(f=2.5)[16]Fig.1 Illustration of virtual-point-detector concept and reconstructed PAT images of simulated targets.(a)Illustration of virtual-point-detector concept；(b)PAT images of simulated targets reconstructed with a point detector， an unfocused transducer， and a focused transducer(f=2.5)[16]

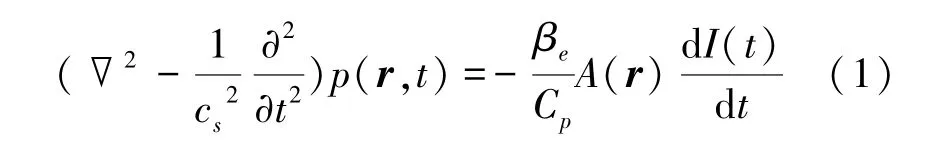
式中,r是成像区域中的一点的位置向量,t是时间,p(r,t)是位置r处在时间t的声压,A(r)是位置r处的光吸收能量,cs是声速,Cp是比热容,βe是等压膨胀系数,I(t)是入射激光脉冲函数。当扫描半径远大于超声波长且入射短脉冲激光的时间分布视为δ(t)时,采用反投影(back-projection,BP)法可根据测量的光声信号重建出光吸收能量分布[16]:

式中,r0是聚焦换能器的位置向量,r′0是虚拟点探测器的位置向量,p(r0,t)是位置r0处、时间t的声压,θ0是换能器在成像平面内进行圆周扫描采集光声信号的角度,df是聚焦换能器的焦距。

与非聚焦换能器相比,聚焦换能器的点扩展函数(point-spread functions,PSF)的切向延伸更窄,因而可提高图像的切向分辨率(见图2),但是牺牲了径向分辨率。此外聚焦换能器的接收角是由其f数决定的,f数也会影响图像的切向和径向分辨率,因此未来的工作中应优化f数以获得最佳图像质量。

2.2 负折射率声透镜

点探测器具有较大的接收角,但由于其有效面积小,在换能器中产生的高热噪声感应电压导致其信噪比较低。相比之下,有限尺寸的非聚焦超声换能器的探测面积大,具有较高的灵敏度和良好的信噪比,但接收角通常较小。利用负折射率声透镜附着在换能器表面上可增大其接收角,与平面探测器相比,图像切向分辨率可提高3 倍以上[17-19],即使在目标远离扫描中心或接近探测器表面的情况下也能在重建图像中复现物体的形状,如图2所示。此外,增大接收角还可以扩大成像范围。

图2 对在距扫描中心不同距离处放置的五个0.5 mm直径的铅笔头的PAT 成像结果(每行左为重建图像，右为局部放大图)[18]。(a)使用平板探测器的重建图像；(b)使用负透镜探测器重建图像Fig.2 PAT images of five pencil tips with the diameter of 0.5 mm placed in the scanning area at different distances from the scanning center(The left are the reconstructed images，the right are their corresponding close-up images)[18].(a)Using the flat detector；(b)Using the negative lens detector

但是,透镜的质量、透镜内的混响以及透镜和探测器表面之间胶膜的缺陷会导致图像中出现伪影。同时,由于负透镜采用丙烯酸制作,其对超声波的吸收可能造成信号损失,声耦合介质矿物油和丙烯酸镜片之间的阻抗失配也会造成一定的信号损失。未来的研究中可考虑将检测超声的压电材料弯曲成凸形,解决上述问题。

2.3 基于模型的图像重建方法

基于虚拟点探测器的方法虽然提高了切向分辨率,但这种改善是以牺牲径向分辨率为代价的,而且切向分辨率也会随着成像目标位置的不同发生变化,因此不适用于大目标(如乳房)的成像。Li等[20-22]提出采用基于模型的图像重建方法解决有限尺寸非聚焦超声换能器所致的径向分辨率下降问题。针对采用有限尺寸非聚焦换能器的PAT 系统,建立二维线性离散成像模型。如图3所示,将成像区域O划分为M×N个点,每个点的值o(xn,ym)是坐标(xn,ym)处的光吸收能量密度。超声换能器进行圆周扫描采集光声信号,每旋转一周采集L个角度的光声信号,一次全角度(360°)扫描得到的完备光声信号集中包括L条A 扫描线。将在角度θl处接收的A 线信号表示为K×1 的矢量yl:

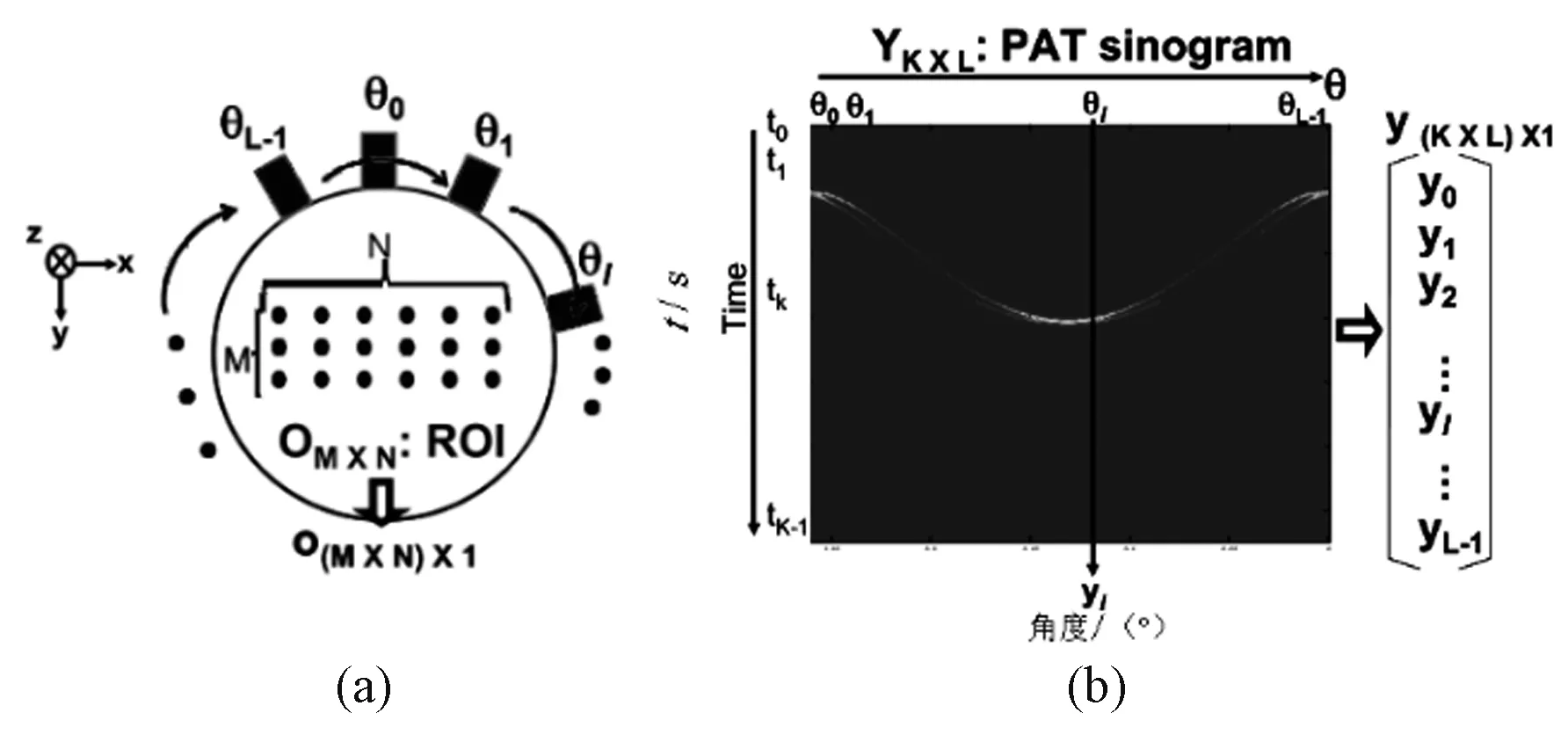
图3 光声信号采集示意图[21]。(a)数据采集；(b)信号矩阵Fig.3 Illustration of sampling of photoacoustic signals[21].(a)Data acquisition；(b)Signal matrix

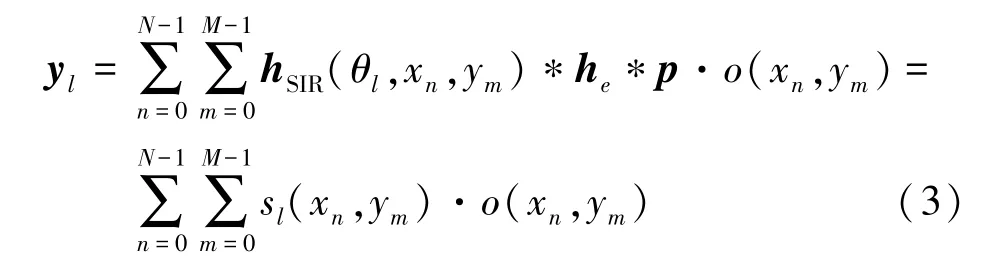
式中,hSIR是从换能器所在位置θl到o(xn,ym)的SIR 矢量,he是换能器的EIR 矢量,p是由介质中的点吸收体产生的单位光声波,可以用单位冲激函数的导数来近似,“*”是卷积运算。式(3)的矩阵表达式即为二维离散成像模型,有

式中,y是(K×L)×1 维的向量,表示探测器接收的信号,o是(M×N)×1 维的向量,表示光吸收能量密度,e是加性噪声向量,S是SIR 矩阵。

假设o和e都是服从高斯分布且互不相关的随机向量,基于式(4)得到最优时空滤波器K[23]:

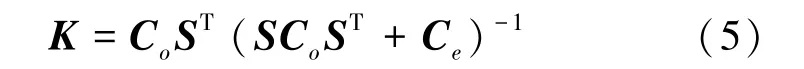
式中,Co和Ce分别是o和e的协方差矩阵。最优时空滤波器的作用是使o和重建图像Ky之间的误差最小。对于光声数据集中的每一点,使用1 与非聚焦换能器的SIR 进行反卷积,恢复退化的切向分辨率。

该方法在保持径向分辨率的同时,可有效改善切向分辨率退化问题,如图4所示。尽管当目标靠近换能器表面时旁瓣电平变得更大,但在所有成像区域上均可提供均匀的PSF 峰值幅度,这一特征对于定量PAT(quantitative photoacoustic tomography,qPAT)非常重要[24]。此外,通过在成像模型中引入换能器的EIR,该方法还有可能提高成像的径向分辨率。但是由于未考虑信噪比和不均匀声速等非理想条件对成像质量的影响,且应用前提是探测器采集到完备的信号数据,因此当只能进行有限角度扫描时,采用该方法重建的图像中存在伪影。

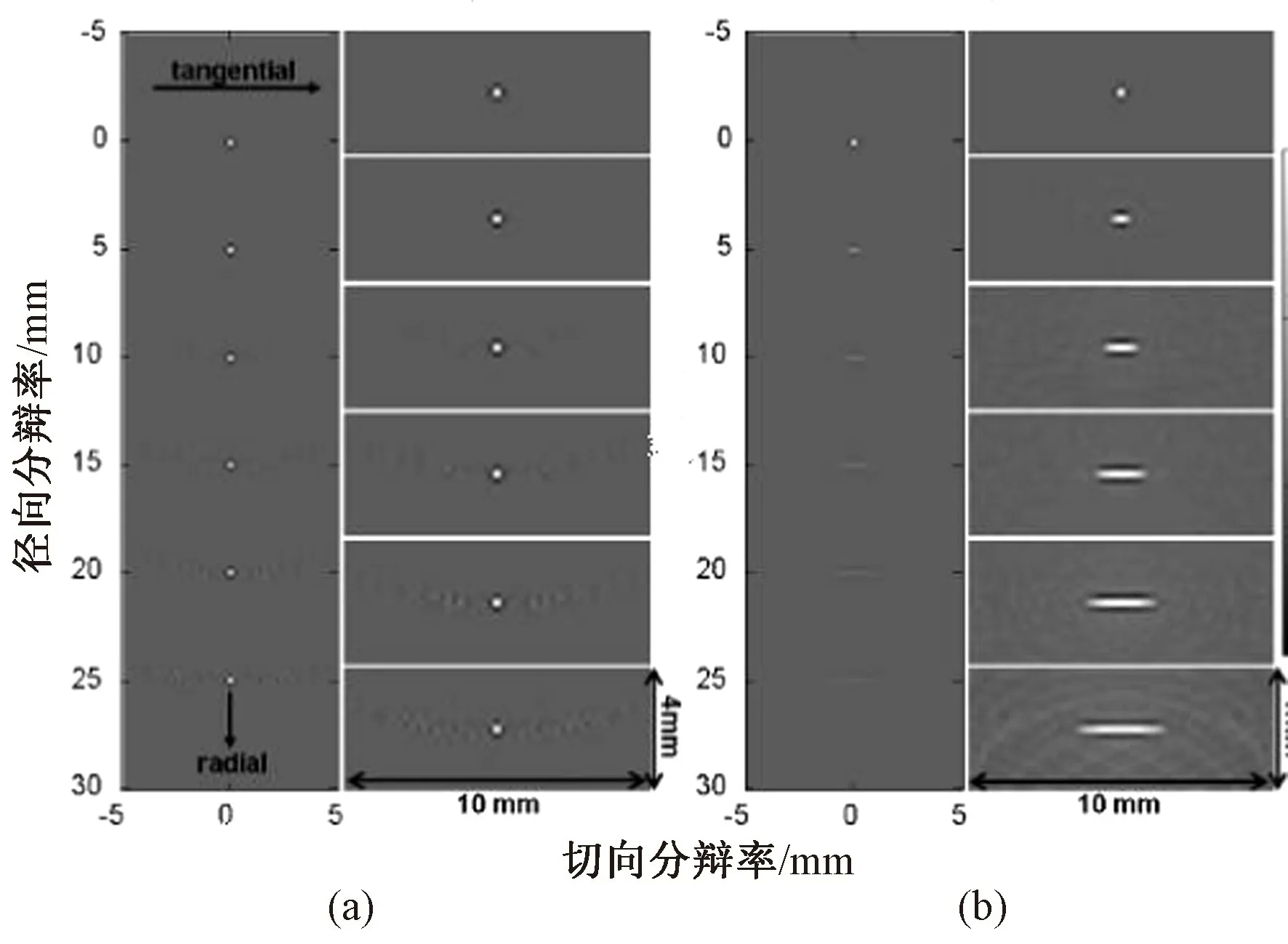
图4 仿真点吸收体的PAT 重建图像[21]。(a)基于模型的校正方法；(b)BP 法Fig.4 Reconstructed PAT images of simulated point-like absorbers[21].(a)Model-based correction method；(b)BP method

2.4 压缩感知法

对于不完备测量数据集,可采用压缩感知法[25]降低重建图像所需数据量,即在式(4)的成像模型中添加新的约束条件得到基于压缩感知的二维线性离散成像模型:

式中,ε是控制重建保真度的常数。通过求解式(6)重建图像,如图5所示。CS 法可减少系统成本和数据采集时间,甚至可以用相同的测量次数覆盖更大的视场,但是其在实验验证中未考虑噪声的影响。

图5 根据60 个扫描角度的光声数据重建的PAT图像[25]。( a)基于模型的方法；( b)BP法；(c)CS 法Fig.5 Reconstructed PAT images from pressure data obtained in 60 scanning viewangles[25].(a)Model-based method；(b)BP method；(c)CS method

3 脉冲响应问题的解决方法

处于接收模式的超声换能器的响应可以用两个独立的分量来表示:EIR 和SIR,其中EIR 表征换能器的电响应,SIR 表征换能器有源区域内的平均效应,它描述了由换能器有限检测表面所致的各向异性检测灵敏度。重建图像时如果不考虑SIR 和EIR,可能导致图像的空间分辨率降低。解决该问题的主要方法是对超声换能器的SIR 和EIR 建模,构造包含EIR 和SIR 的成像模型,然后通过模型反演重建图像[14,26-40]。

假设目标具有均匀声学特性、忽略声衰减且I(t)=δ(t),则光声波动方程式(1)的解可以表示为理想点探测器记录的声压[14],有

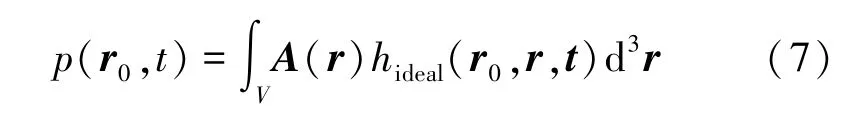
其中

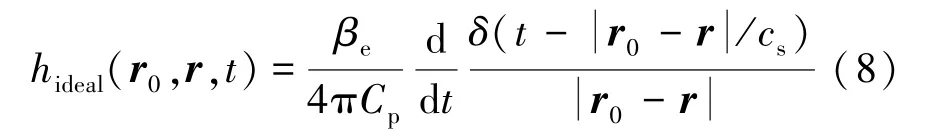
式中,V是成像目标体,r0是理想点探测器的位置向量,hideal(r0,r,t)是在理想点探测器的假设前提下成像系统的响应函数,表示在时间t=0 时由位置r处的点声源产生、并被位置r0处的理想点探测器在时间t＞0 记录的光声波场。式(7)是连续形式的理想成像模型,求解式(7)的逆问题,即根据p(r0,t)估计A(r),即实现图像重建。

为了建立考虑探测器响应的离散成像模型,将非理想点探测器视为线性声学系统,根据到达探测器表面的声压得到其产生的电压信号:

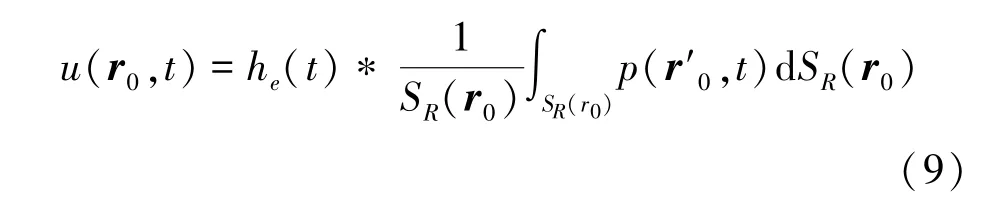
式中,u(r0,t)是中心位于r0的探测器在时刻t产生的电压,he(t)是探测器的EIR(单位:V/Pa),SR(r0)是探测器的有效面积,“*”是时域卷积运算。将式(7)和式(8)代入式(9),有

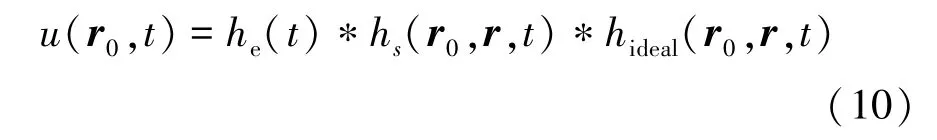
式中,hs(r0,r,t)是SIR。考虑探测器响应的离散成像模型表示为

式中,向量u∈RM表示探测器的采样电压信号,向量长度M是在每个测量位置采集的时间样本数S与测量位置数Q的乘积,ua表示u中的第a个元素,H是A(r)映射到u的系统矩阵,θ是系数向量。采用惩罚最小二乘(penalized least-squares,PLS)算法求解式(11)的逆问题,从u中得到θ的估计值[14],有

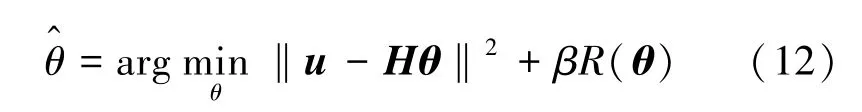
式中,R(θ)是正则化项,β是正则化参数。根据θ的估计值可得到对A(r)的估计。

采用该方法可在不降低空间分辨率的情况下消除探测器尺寸对图像空间分辨率的影响,解决使用大检测面积或紧凑测量几何的探测器所致空间分辨率下降的问题,与基于点探测器的算法相比,即使在目标的外围区域,图像中的目标边缘仍然非常清晰,如图6所示。

图6 使用不同系统矩阵从无噪声数据中重建的PAT图像[14]。(a)SIR 为δ(t)；(b)EIR 为δ(t)；(c)SIR和EIR 均为δ(t)；(d)SIR 和EIR 均非δ(t)Fig.6 PAT images reconstructed from noiseless data by using different system matrices[14].(a)SIR is δ(t)；(b)EIR is δ(t)；(c)Both SIR and EIR are δ(t)；(d)Neither SIR nor EIR is δ(t)

为了降低上述算法的计算量,可在成像模型中加入远场近似,并且通过将探测器表面划分成多个大小完全相同的块,避免当目标位于探测器的近场区域内时图像中出现近场伪影[26],如图7所示。但是在某些应用中对声衰减以及声速和密度不均匀性的补偿很重要,因此还应考虑如何构造更能反映介质声学特性的系统矩阵。

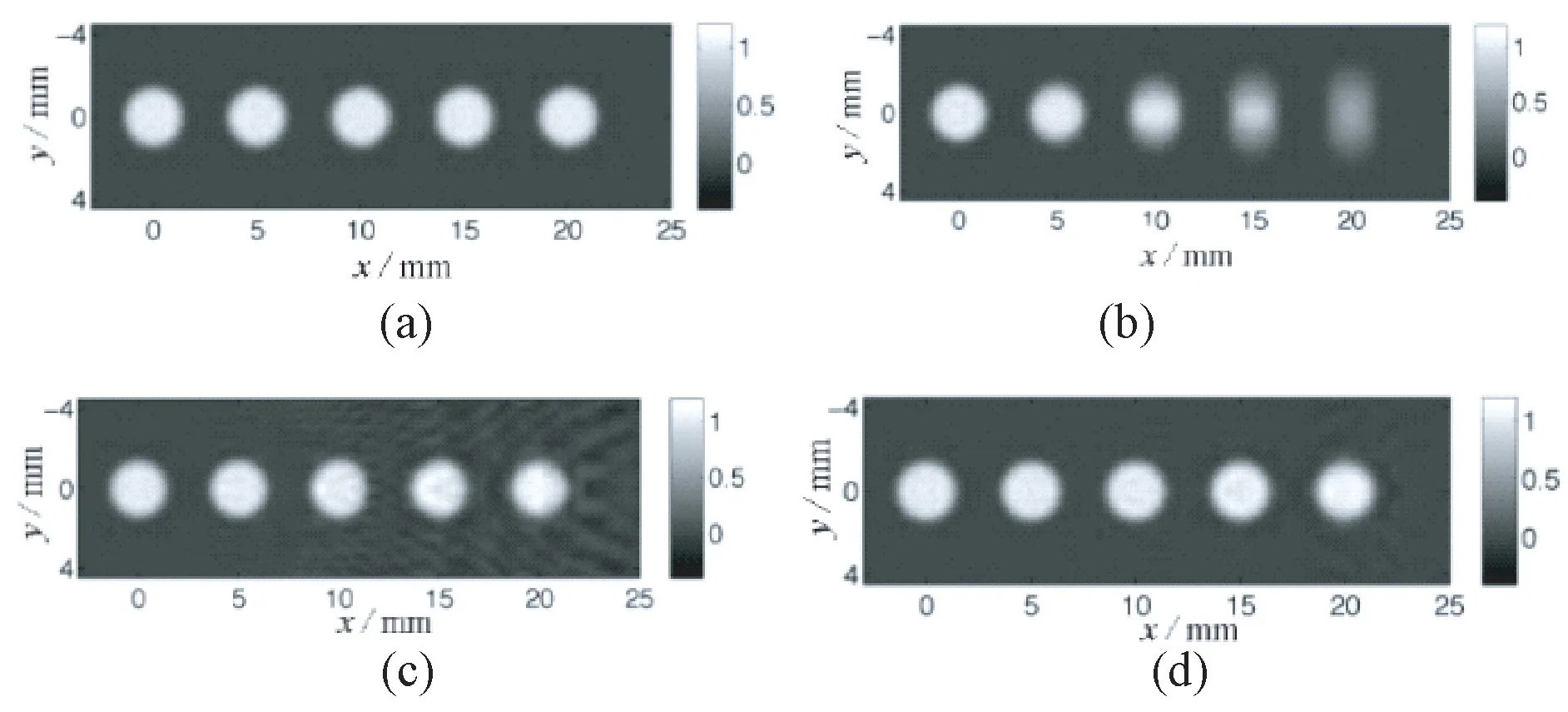
图7 采用基于远场近似的成像模型的图像重建结果[26]。(a)仿体图像；(b)基于点换能器的重建图像；(c)基于远场近似的重建图像；(d)对换能器表面进行划分后的重建图像Fig.7 Images reconstructed by using the method based on far-field approximation[26].(a)Original phantom image；(b)Image obtained by using the point-like transducer approximation；(c)Image obtained by using the far-field approximation；(d)Image obtained by using the far-field approximation after patching

通常通过实验测得超声换能器的EIR,当测量存在误差时,会降低系统矩阵H的精度,进而导致图像中存在伪影或失真。为了解决该问题,Sheng等[27-28]将式(11)的成像模型改写为

式中,h是用向量表示的EIR 值,H(h)是系统矩阵。该成像模型具有双线性结构,图像重建表示为如下的数值优化问题:

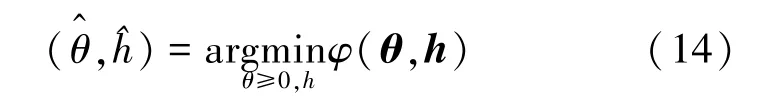
其中

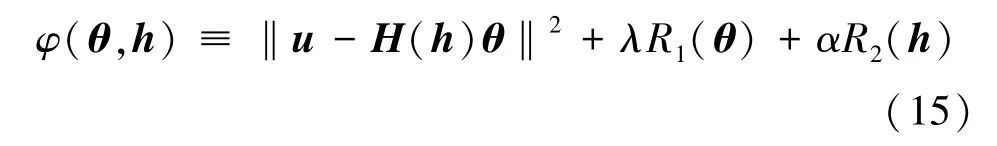
式中,R1(θ)和R2(h)是正则化项,λ和α是正则化参数。将式(14)中的优化问题转化为求解如下两个问题:

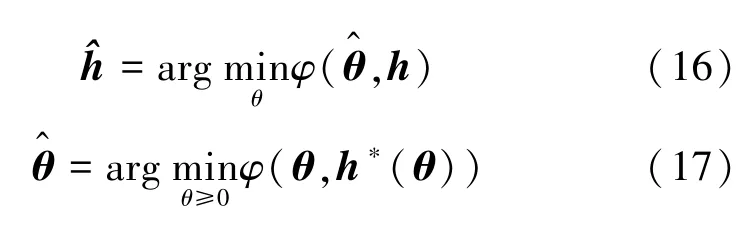
其中

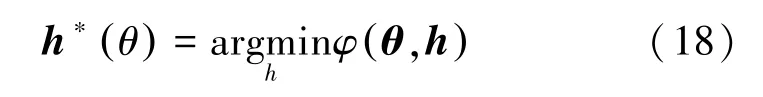
使用变量投影(variable projection,VP)法[29]求解式(16)和式(17),得到θ的估计值,进而重建光吸收能量分布图。该方法可同时估计A(r)和EIR,提高重建图像的保真度(见图8),即使由于声速变化、声吸收或换能器的SIR 导致模型出现误差,VP也可以粗略校正,因此它可以作为一种低成本而有效的方式来补偿模型失配。但是该方法中涉及两个正则化参数,需合理选择才能得到满意的重建结果。

图8 采用含噪声数据重建的图像[27]。(a)仿体图像；(b)迭代法重建图像；(c)VP 法重建图像Fig.8 Images reconstructed from noisy data[27].(a)Phantom image；(b)Image reconstructed by using the iterative method；(c)Image reconstructed by using the VP method

如前所述,采用负透镜制作的负聚焦(negatively focused,NF)探测器[16-18]虽然可以提高图像的切向分辨率,但由于缺乏精确的图像重建公式,因此通常假设NF 探测器测量的信号与位于探测器几何中心的虚拟点探测器测量的信号相同,进而完成近似图像重建。在此过程中NF 探测器的SIR 会导致图像中出现伪影,采用上述基于模型的图像重建方法可去除此类伪影[30-31],如图9所示。

图9 对采用NF 探测器的PAT 图像重建结果[31]。(a)不同尺寸和强度的高斯吸收体仿真图像；(b)采用优化声速法重建的图像；(c)采用时间微分法重建的图像；(d)采用基于模型的方法重建的图像Fig.9 Results of image reconstruction for PAT system equipped with a NF detector[31].( a)Gaussian absorbers of various sizes and intensities；(b)Image reconstructed with the method of optimizing sound speed；( c)Image reconstructed with the time differential method；(d)Image reconstructed with the model-based approach

4 方向性问题的解决方法

PAT 系统中通常采用有限尺寸的超声探测器,其并不只对压力变化产生响应,而是对声压和压力梯度(或其它导数)的组合产生响应,因而具有方向依赖性,即对某些角度的压力波不敏感,但对与探测器表面垂直方向上的压力波最敏感。在这种情况下,测量数据是探测器表面上的声压及其法向导数的线性组合,可通过建模将探测器的方向相关性包含在测量数据中,进而求解初始声压分布[41]。

建立测量信号模型,有

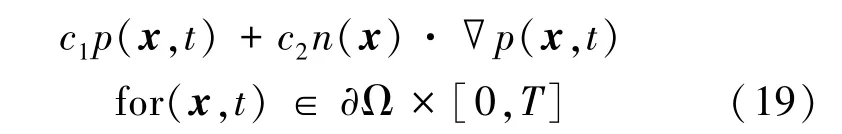
式中,Ω是完全或部分包围成像目标的测量面,x∈∂Ω 是探测器的位置,p(x,t)是目标中的光吸收体产生的声压,t是时间,T是测量时间界限,n(x)是在x处指向测量面外的法向矢量,n(x)·∇p(x,t)是声压的法向导数,c1和c2是常数。p(x,t)满足下列初始条件

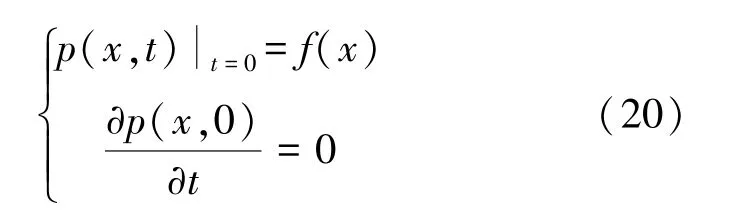
式中,f(x)是位置x处的初始声压。图像重建的目的是从满足式(19)的声压数据p(x,t)中重建初始声压f(x)。标准图像重建问题对应于式(19)中c1≠0 和c2=0 的特殊情况。对于c1和c2可在实数范围内任意取值且测量曲面为球面的情况,Zangerl等[41]利用Fourier-Bessel 级数推导出了级数展开形式的重建表达式

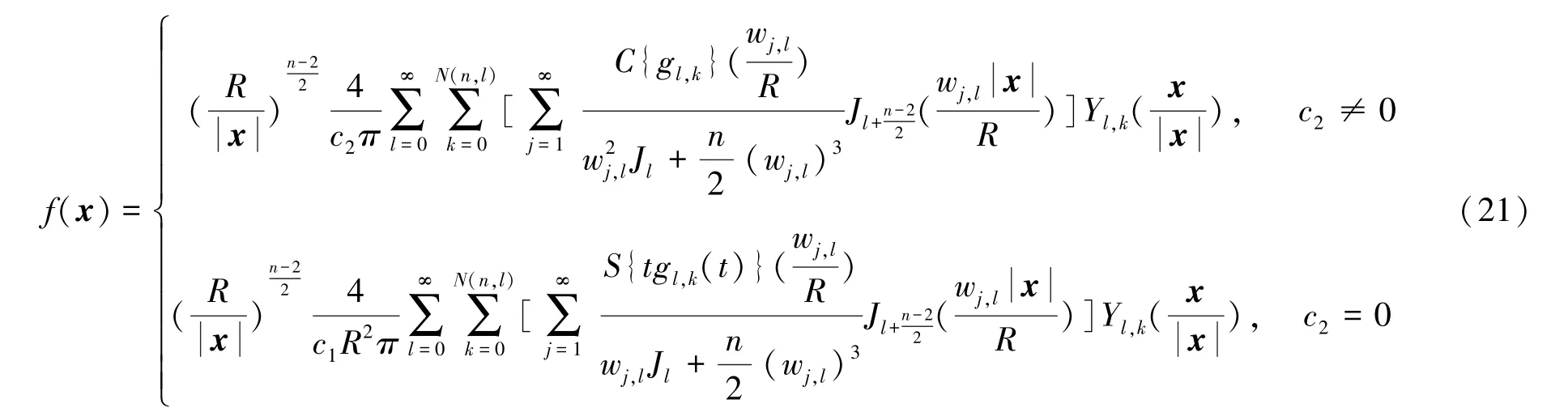
式中,R是球形测量面的半径,Jl是l阶第1 类Bessel 函数,wj,l是Jl+(n-2)/2的第j个正根,Yl,k是球谐函数,gl,k(t)是测量数据,C{gl,k}和S{tgl,k(t)}分别是gl,k的余弦变换和正弦变换,N(n,l)的定义为

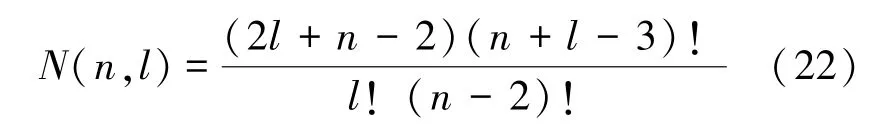
且N(n,0)= 1。如图10所示,采用该方法可以校正探测器的方向性对图像重建质量的影响。但其只针对球面测量面,且假设测量时间界限T=∞,因此不具有一般性。后续需研究针对更一般的检测几何以及t＜T＜∞时测量数据的重建公式。

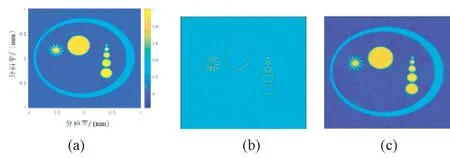
图10 校正探测器方向性的仿真实验结果[41]。(a)初始声压的前向仿真图像；(b) c2=0 的重建结果；(c) c2≠0 的重建结果Fig.10 Results of noisy data reconstruction by using the correction method for direction dependence[41]( a)Simulated initial pressure distribution map；(b)Exact reconstruction for c2=0；(c)Exact reconstruction for c2≠0

5 扫描半径

采用半径标定法[42]可确定每个探测器的扫描半径,在每个测量位置采集A 扫描线上的光声信号,计算点声源和探测器之间的距离,有

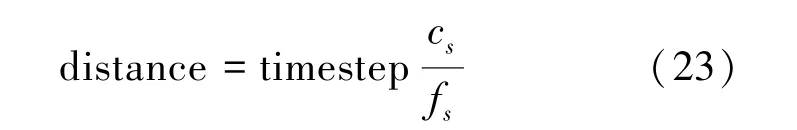
式中,timestep 是时间步长,cs是声速,fs是采样频率。根据式(23)计算直径两端的换能器和点光源之间的距离,最近的距离为r1,最远的距离为r2,如图11所示(图中SUT 代表换能器)。然后,得到换能器的重建半径,有

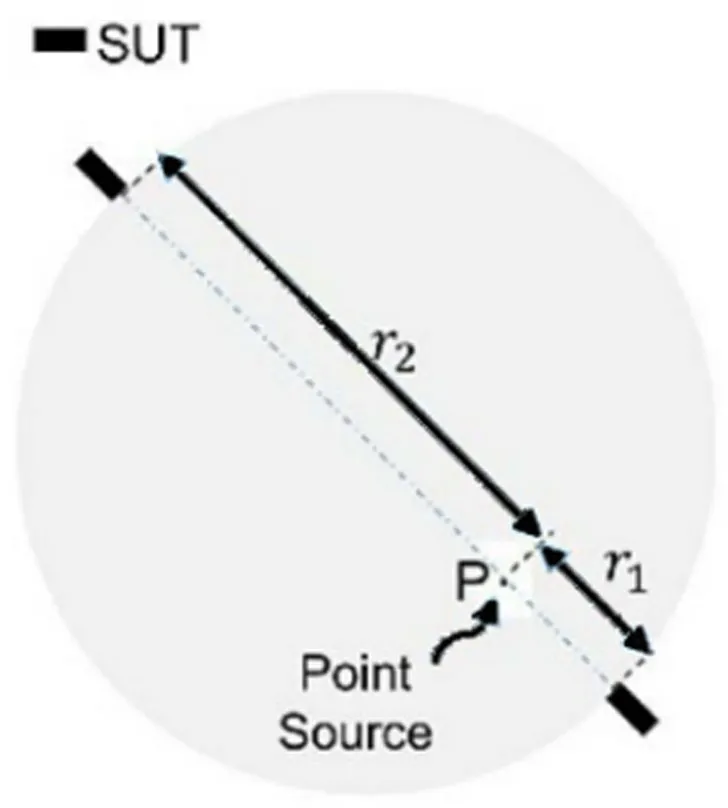
图11 采用点源P 量化扫描半径的示意[42]Fig.11 Schematic diagram of quantification of the scanning radius by using a point source “P”[42]

半径标定方法可以自动寻找每个探测器的扫描半径,校正使用单一半径造成的图像失真,如图12所示。该方法应用于多阵元换能器圆形扫描PAT 系统,比使用单阵元换能器更高效、比环形换能器阵列更经济。但是由于校准方法还取决于超声波在介质中的传播速度,因此若介质发生变化,需要重新标定扫描半径。

图12 对仿真血管网络模型的光声图像重建结果[42]。(a)仿真血管网络；(b)使用SUT1 获得的光声数据的重建图像；(c)使用SUT1 和SUT2，没有半径补偿的图像；(d)使用SUT1 和SUT2，经过半径补偿的图像Fig.12 Results of photoacoustic image reconstruction for numerical phantom of vessel network[42].(a)Numerical phantom；(b)Image reconstructed from data obtained by SUT1(c)Image reconstructed from data obtained by SUT1 and SUT2 without radius compensation；(d)Image reconstructed from data obtained by SUT1 and SUT2 with radius compensation

6 有限视角和有限带宽

采用加权因子法[43]、迭代滤波反投影法[44]和压缩感知[45]等方法可减少PAT 图像中的有限视角伪影,但是加权因子法不适用于平面探测器阵列,迭代滤波反投影法和压缩感知法的计算成本过高。对于有限带宽伪影,采用维纳滤波[46]可扩展检测信号的频谱,但是其对检测信号信噪比的要求很高,在实际应用中可能不适用。Rejesh 等[47]提出了一种迭代反卷积法消除图像模糊,但所需的运算时间较长。

近年来,深度学习技术在重建高质量图像方面表现出了巨大潜力。为了减少PAT 图像中的有限视角伪影,可构建卷积神经网络(convolutional neural network,CNN)模型(如UNet)对低质量图像进行后处理[48],或者将CNN 作为求解优化问题的工具,将输入的光声信号测量数据直接映射为高质量的输出图像,达到优化重建的目的[49]。例如,Gutta 等[50]应用全连接神经网络从射频数据中提取带外信号,减少有限频带响应对成像质量的影响。为了同时减少有限视角伪影和有限带宽伪影,Vu等[51]构建了稳定的、具有梯度惩罚的Wasserstein 生成对抗网络( wasserstein generative adversarial network with gradient penalty,WGAN-GP),如图13所示,其中Wasserstein 度量用于解决梯度消失问题,采用均方误差损失函数保持重建图像的信息

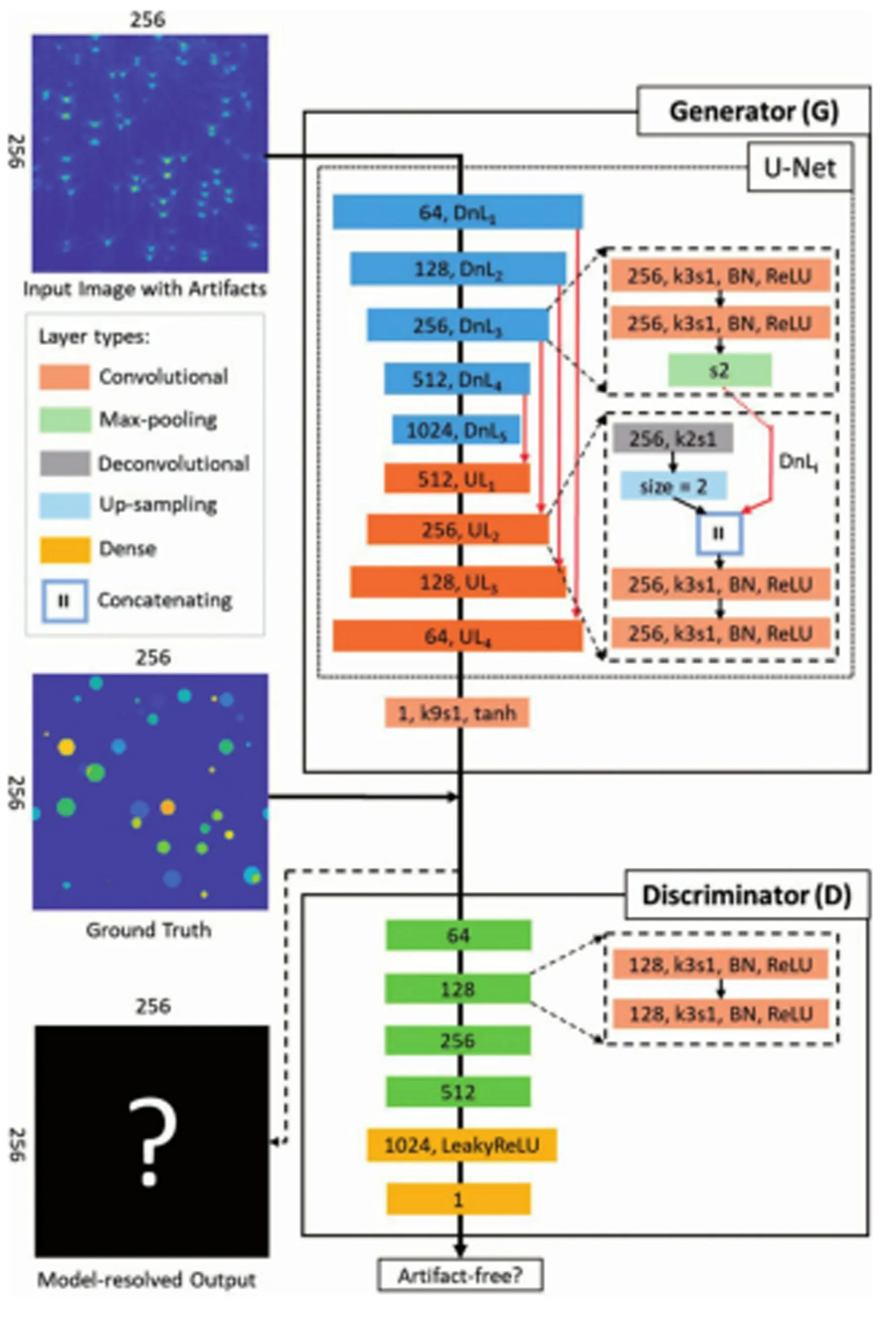
图13 WGAN-GP 模型体系结构[51]Fig.13 WGAN-GP model architecture[51]

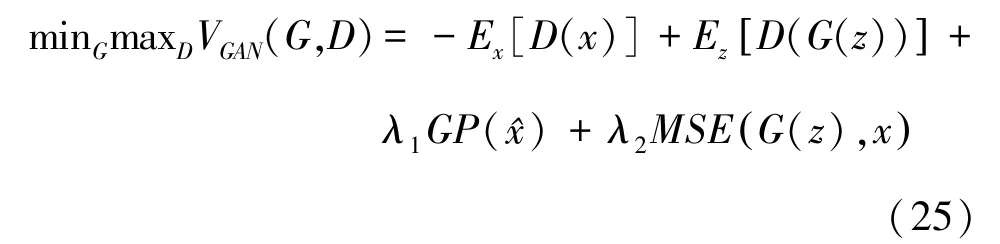
其中

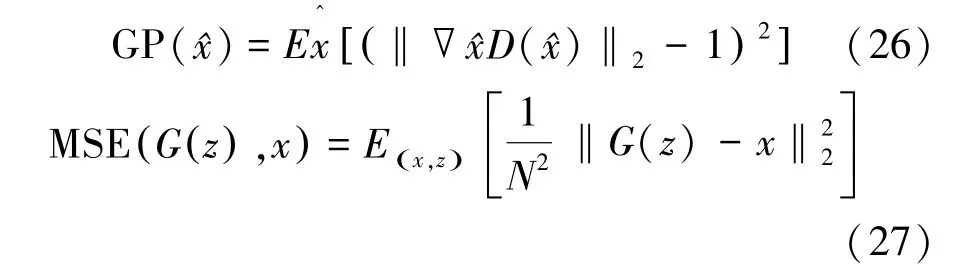
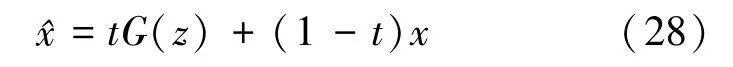
式中,D和G分别是生成网络和判别网络,E(·)是期望运算符,x是无伪影图像,z是采用时间反演法重建的含伪影图像,^x是以t为时间间隔从G(z)中采样的值,t服从[0,1]区间上的均匀分布,N是像素总数,λ1和λ2是权重参数。

WGAN-GP 模型在不改变成像系统或降低成像速度的前提下,可以有效减少PAT 图像中的有限视角伪影和有限带宽伪影,如图14所示。然而,该方法的正向模型中没有考虑光激发,且重建活体图像结构的保真度差。此外,深度学习网络的目标是指定的,只能识别与训练数据中使用的目标相似的目标。后续需研究更通用的训练数据,提高网络的适应性。

图14 采用WGAN-GP 重建双光子显微血管图像的结果[51]。(a)仿体图像；(b)时间反演重建图像；(c)UNet 重建图像；(d)WGAN-GP 重建图像Fig.14 Reconstruction results of simulated twophoton microscopy vascular images with WGANGP[51].(a)Phantom image；(b)Time-reversal reconstruction；( c)UNet reconstruction；( d )WGAN-GP reconstruction

7 探测器位置的不确定性

为了降低探测器位置的不确定性在图像重建中引入的误差,Sahlstrom 等[52]提出了基于贝叶斯近似误差建模的方法。根据贝叶斯定理,PAT 逆问题的解表示为如下的条件概率密度函数,有

式中,pt是探测器测得的声压时间序列,p0是初始声压,π(p0｜pt)是后验概率密度,π(pt｜p0)是似然概率密度,π(pt)是归一化常数。

图像重建问题转化为求解π(p0｜pt),建立考虑探测器位置不确定性的成像模型:

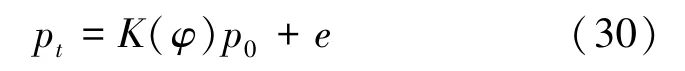
式中,e是加性测量噪声,K(·)是前向算子,随机变量φ是不确定度参数。φ通常被固定为常量φ0,因此式(30)改写为

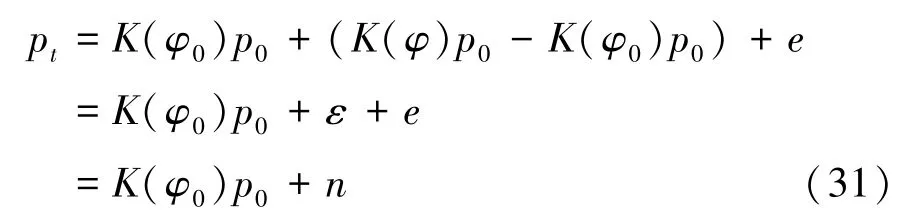
式中,ε是描述精确模型和不精确模型之间差异的近似误差,n是总误差。假设ε和n都服从高斯分布,忽略ε对p0的依赖,根据式(31),得到似然概率密度,有

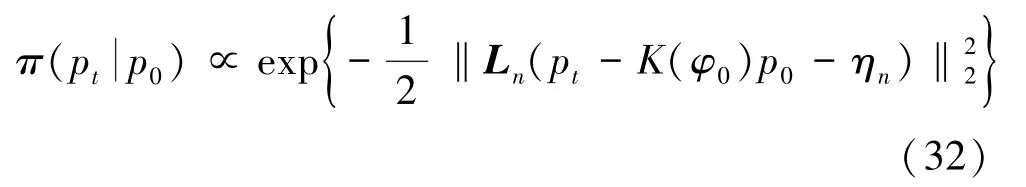
式中,Ln是总误差的逆协方差矩阵的Cholesky 分解,ηn是总误差n的均值。后验概率密度π(p0｜pt)的表达式为:

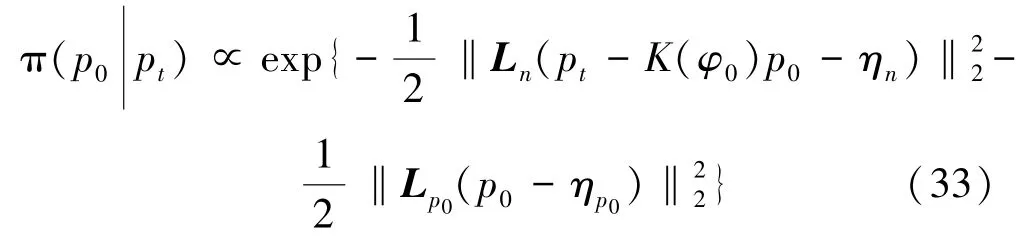
该方法在建模时考虑了探测器的脉冲响应,在难以准确测量探测器位置的情况下,可以校正探测器位置的不确定性对图像质量的影响,如图15所示。但是,统计建模误差时比较耗时。

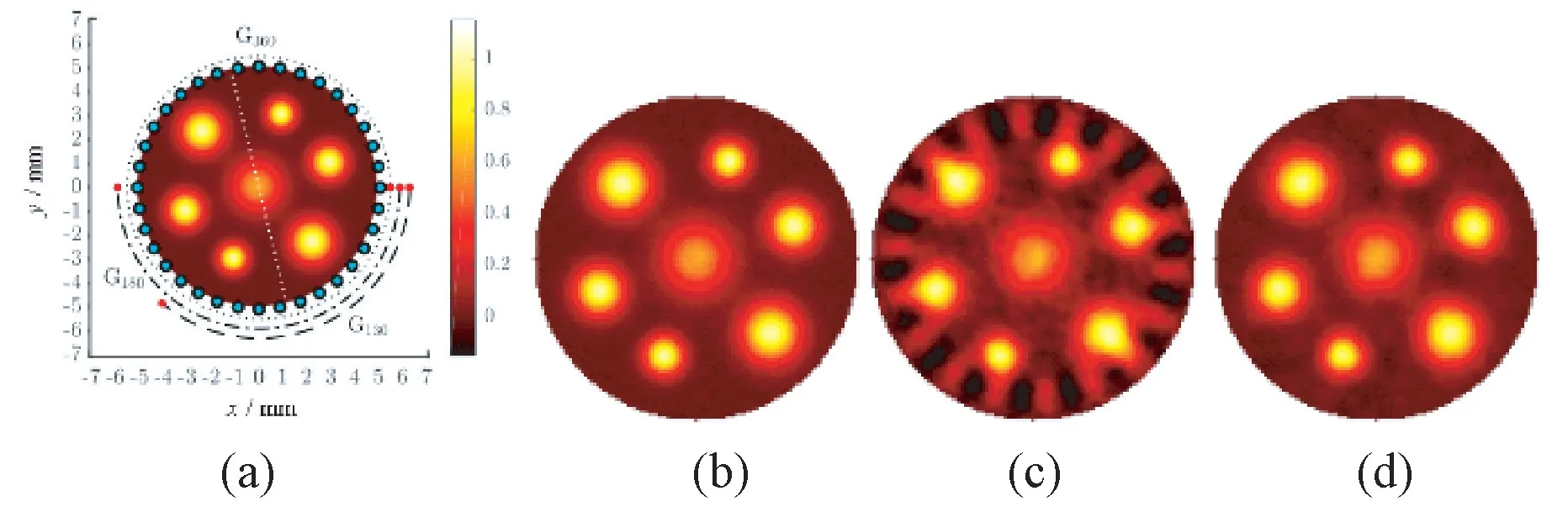
图15 采用不同误差模型的图像重建结果[52]。(a)仿真初始声压分布图和探测器的位置；(b)采用精确常规误差模型的重建图像；(c)采用不精确常规误差模型的重建图像；(d)采用增强型误差模型的重建图像Fig.15 Results of image reconstruction by using different error models[52].( a)Simulated initial pressure and sensor geometries；( b )Image reconstructed by using an accurate conventional error model；( c )Image reconstructed by using an inaccurate conventional error model；( d)Image reconstructed by using an enhanced error model

8 结论

文中针对忽略超声探测器的有限孔径效应、脉冲响应、方向性、扫描半径、有限视角和有限带宽以及位置的不确定性等造成的PAT 重建图像质量下降问题,归纳和总结了主要的解决方法。

目前,该领域仍然面临着诸多问题,例如:多数方法不具有一般性,只针对特定应用场景中的特殊成像几何；重建算法与成像模型的不匹配导致重建效果不理想；与探测器的SIR 不同,很难用一个相对简单的物理模型来精确描述EIR,虽然已经提出了描述EIR 的多种理论模型[32],但是这些模型中采用的参数在实际中很难甚至不可能精确测量[28],因此在PAT 的应用中,通常对EIR 进行实验测量。虽然概念上很简单,但是EIR 的测量极易受到噪声和其它误差的影响,进而降低图像质量[53]。

此外,入射激光脉冲的持续时间、测量表面的完整性和连续性以及组织中声速的不均匀性、光衰减和光通量分布不均匀等都会影响图像重建的质量。因此,在图像重建过程中,为了提高成像质量,需要综合考虑多方面因素,将解决上述问题的方法进行有机结合,充分发挥各自的优势。同时,随着深度学习和大数据技术的飞速发展,今后的发展趋势是将非理想条件下的光声成像物理模型包含到深度神经网络的构建和训练中[54],使网络可以从测量数据中学习用于图像重建的先验知识,提高图像重建的质量和速度。