不平衡数据多粒度集成分类算法研究*

陈丽芳，代 琪，赵佳亮

(华北理工大学理学院,河北 唐山 063210)

1 引言

不平衡数据分类问题是机器学习和数据挖掘领域的研究热点，不平衡数据集指的是数据集中各类别的样本数量不均衡，导致学习机学习少数类样本信息量不足，严重影响传统分类算法的分类性能[1]。传统分类算法虽然在结构上存在一定差异，却共同遵循误差最小化原则。在平衡数据集上，采用误差最小化原则能够得到最优结果，针对不平衡数据，此原则将会导致分类面向多数类偏移，难以得到准确的分类结果[2]。传统分类器不能有效地表现不平衡数据集的结构特征，难以确定不平衡数据集的真实分类边界，导致少数类样本分类精度降低。

集成学习(Ensemble Learning)融合了多个弱学习机的学习框架，与传统分类器相比，集成学习框架下的分类器具有更高的泛化性能和分类精度。曹雅茜等[3]利用高斯混合分布的概率模型构造平衡数据集，扩大少数类样本的潜在决策域，过滤冗余噪声特征，并对错分样本和剩余特征赋权，通过加权集成策略获得最终分类结果。陈圣灵等[4]根据基分类器分类结果对少数类样本进行过采样，增大少数类样本的权重，并借鉴Focal Loss思想根据基分类器分类结果直接优化自适应提升算法Adaboost(Adaptive boosting)权重，提升分类器的分类精度。Borowska等[5]提出一种新颖的粗粒度计算方法，通过形成信息粒，并分析其在少数类样本中的包容程度，获得给定问题的分类结果。Barua等[6]提出一种多数加权少数样本的过采样算法MWMOTE(Majority Weighted Minority Oversampling TEchnique)，以信息丰富但难以学习的少数类样本为基础，根据欧氏距离确定此类样本与多数类样本之间的权重，使用聚类算法从已经赋权的少数类样本中生成样本，从而提升模型的分类性能。Alam等[7]提出一种基于递归的集成分类算法，并将其应用于多类不平衡数据分类问题，分析结果表明，该算法在多类分类问题或不平衡数据回归分析中具有更高的性能。张宗堂等[8]通过随机子空间法提取训练样本集，在各训练子集上构建基分类器，在Adaboost集成框架下，迭代形成最终集成分类器。郑建华等[9]采用混合采样策略提升随机森林基分类器多样性，在采样后的平衡子集上训练子树，构建改进的随机森林算法。Zhu等[10]提出基于树的空间划分算法SPT(Space Partition Tree)，将数据递归划分为2个子空间，并在集成框架下构建分类模型，通过合并所有决策子空间，为原始问题提供了新的决策域。Collell等[11]将阈值移动技术与Bagging集成分类算法结合，引入决策阈值移动方法，利用后验概率估计不平衡数据分类的最大性能。Zhu等[12]利用相空间重构方法构建高维特征空间分布模型，通过随机森林选择不同特征进行分类，并输出具有不同属性特征的分类结果。Wang等[13]提出一种迭代度量学习IML(Iterative Metric Learning)方法，探索不平衡数据之间的相关性，构建有效的分类数据空间，寻找最稳定的邻域，从而提升分类模型的分类精度。

目前，对于序贯三支决策的分类算法已有少量研究[14]，主要是将序贯三支决策作为分类器，通过计算样本分类代价，对样本进行分类，当不确定域为空集时，模型分类结束。虽然该算法在平衡数据集上能够有效地分类，但针对不平衡数据，尤其是高度不平衡数据，该算法难以合理地设置代价矩阵和少数类样本的决策代价，直接应用该算法处理不平衡数据，仍然存在难以识别少数类样本、分类精度偏低的问题。因此，将序贯三支决策的粒化思想作为数据预处理方法，在集成学习框架下，分别以各粒层空间中粒化数据作为基分类器的训练集，构建粒化基分类器，能够有效地提升对不平衡数据的分类精度。

集成学习是目前常用的不平衡数据分类框架，与传统分类器相比，在处理不平衡数据方面，具有更高的分类性能和泛化能力[15,16]。学者们主要从改变赋权方法和提升基分类器差异性2个角度提升模型的分类精度。文献[3-7]使用新的赋权方法改变样本或基分类器的权重，从而提升集成分类算法的分类性能。文献[8-13]通过不同的数据划分方法，提高集成分类算法基分类器的差异性。空间划分在一定程度上可以有效提升模型的分类精度，但存在稳定性差、泛化能力弱等问题。

因此，本文提出基于序贯三支决策的多粒度集成分类算法MGE-S3WD(Multi-Granularity Ensemble classification algorithm based on Sequential Three-Way Decision)，通过序贯三支决策粒化数据集可以有效地提升训练子集的差异性，降低数据集的不平衡比，从而提升算法的稳定性和泛化能力。首先，利用二元关系逐层添加属性，实现数据集的动态划分；其次，构建代价矩阵，计算正域、边界域和负域的阈值，形成多层次粒结构；再次，对各粒层空间上的数据子集按照定义的融合规则，形成新的空间划分训练子集；最后，在各训练子集上构建基分类器，并对基分类器分类结果进行集成，获得最终分类结果，以KEEL不平衡数据库(Knowledge Extraction based on Evolutionary Learning imbalanced data sets)中的不平衡数据集作为实验数据，验证算法分类性能。

2 预备知识

2.1 序贯三支决策

三支决策[17]是处理不确定复杂问题的有效策略，其主要思想是“三分而治”，即将一个整体划分为3个相互独立的区域，根据不同区域的特征选择不同的处理方法。序贯三支决策[18]是一种处理动态决策问题的模型，根据层次粒结构的序关系可以分为3种情况：自顶向下、自底向上和自中向外。自顶向下是一种常见的粒结构解决方法，主要是从低层次粒度向高层次粒度发展。

根据n个等价关系，可以在不同的条件属性集下得到论域的不同划分，且满足：

[X]Cn⊆…⊆[X]C2⊆[X]C1

(1)

其中，X表示多个样本的矩阵形式， [X]Ci表示不同条件属性下得到信息粒，Ci,i=1,…,n为条件属性集，Cn表示使用所有条件属性进行划分，以此类推。

由此可以得到一个n层的粒结构，可以表示为：

GS=(GS1,GS2,…,GSn)

(2)

GSi=(Ui,Ei,Ci,[X]Ci)

(3)

其中,GSi表示第i个粒结构，Ui为粒结构中的非空有限集，Ei为Ui中存在的等价关系，同样，此处的Ci表示粒结构中的条件属性集。

在多层次粒结构中，每一层属性的选择方式取决于动态决策任务的目标。在序贯三支决策中，对划分到边界域的对象，只有最后一层采用二支决策，其余粒层均采用三支决策。因此，需要根据实际情况，在每个粒层上分别设置合理的三支决策阈值[19]。

(4)

(5)

BND(αi,βi)(vi)=

{x∈Ui+1|βiivi(Desi(X))iαi}

(6)

其中,x表示待决策样本，viDesi(X)表示待决策对象集，POS(αi,βi)(vi)表示正域，NEG(αi,βi)(vi)表示负域，BND(αi,βi)(vi)是边界域，边界域中的对象均被延迟决策。随着从低层获取更多的信息，边界域逐渐缩小，对象逐渐从BND被划分到POS和NEG。最终在最底层实现简单的二支决策。

定义2[14]给定一个决策表S=(U,Ct=C∪D,{Va|a∈Ci},{Ia|a∈Ci})，假设有n+1层粒层空间，n≥1,在决策表S上的粒化定义为：

G={g(Ci)|Ci⊆C}

(7)

其中，g(Ci)为某一特定相同粒度的信息粒集合对U的划分，C为决策表中条件属性集，D为决策表中决策属性集，Va为每个属性a∈Ci的值的集合，Ia为每个属性a∈Ci的信息函数，Ci,1≤i≤n，是条件属性子集，且满足条件C1⊂C2⊂…⊂Cn⊂Cn+1=C。

2.2 集成学习

集成学习是一种机器学习框架，通过构建并结合多个学习机完成学习任务，从而获得比单一学习机更好的泛化性能。根据各基学习机数据之间是否存在依赖关系，集成学习可以分为2类：一类是具有强依赖关系的学习算法，以boosting算法为代表[20]；另一类是不存在依赖关系的学习算法，以随机森林为代表[21]。根据不同的数据集，可以选择“同质”弱学习机，也可以选择“异质”学习机，较多研究者更倾向于选择“同质”弱学习机进行集成学习[22]。CART(Classification And Regression Trees)决策树具有较高的分类精度和稳定性，因此本文选择CART决策树作为集成分类算法的基分类器。

3 算法设计与模型构建

3.1 算法设计

基于序贯三支决策的多粒度集成分类算法MGE-S3WD流程图如图1所示。其中，Ai表示条件属性集C中的第i个属性。

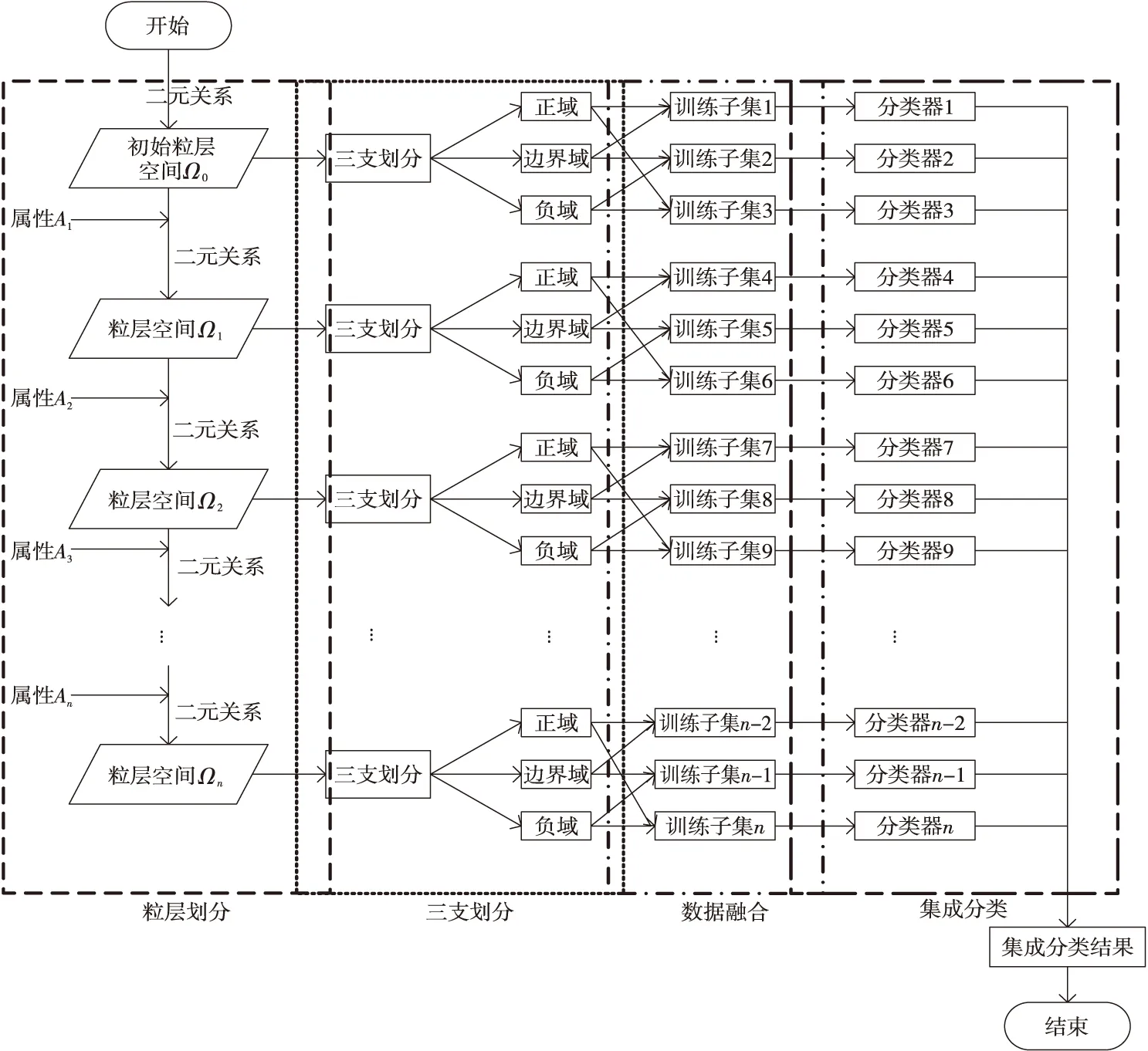
Figure 1 Flowchart of multi-granularity ensemble classification algorithm based on sequential three-way decision图1 基于序贯三支决策的多粒度集成分类算法流程图

该算法具体流程描述如下：

(1)数据集粒层划分。

Step 1数据集中各属性之间的量纲或取值范围存在一定差异性，因此，为了避免这些因素的影响，利用最大-最小归一化方法对数据集中的数据进行归一化处理，如式(8)所示：

(8)

Step 2文献[23-25]中将属性均匀离散为3个区间，且分类或回归性能较好。因此，本文按照此方式对属性进行离散化处理。如果需要更细的划分，可以选择更多的粒化区间，粒化区间越多，粒层空间越细，划分过程的时间复杂度越高。

Step 3选择2个属性作为初始属性集，使用二元关系的交运算(如式(9)所示)划分粒层空间，形成初始粒层空间Ω0，并逐层添加属性，动态划分数据集，最终形成n个粒层空间Ωn。

令R和S是U上的2个二元关系，定义二元关系的交运算[26]为：

R∩S={(x,y)|xRy∧xSy}

(9)

(2)粒层空间上的三支划分。

Step 4[27]设置决策结果的代价矩阵，如表1所示。

Table 1 Cost matrix表1 代价矩阵

其中，xC(P)表示类别C中属于正类P的样本；xC(N)表示类别C中属于负类N的样本；λPP表示将正类样本分到正域的代价；λBP表示将正类样本分到边界域的代价；λNP表示将正类样本分到负域的代价；λPN表示将负类样本分到正域的代价；λBN表示将负类样本分到边界域的代价；λNN表示将负类样本分到负域的代价。

Step 5[27]根据式(10)和式(11)计算阈值α和β。

(10)

(11)

Step 6[27]根据式(11)计算对应粒层空间上各区域的条件概率，并将粒层空间上的子空间划分为正域、边界域和负域。

(12)

因此，当Pr(Si)≥0.75时，数据子集Si为正域；当0.75>Pr(Si)>0.4时，数据子集Si为不确定域；当Pr(Si)≤0.4时，数据子集Si为负域。

(3)粒层空间上融合数据子集。

Step 7分别将初始粒层空间Ω0至第n层粒层空间Ωn上的子集按照正域与边界域、正域与负域、边界域与负域组成新的训练子集Di。

算法伪代码如算法1所示：

算法1不平衡数据多粒度集成分类算法

输出：测试集集成分类结果。

1.functioncalculateP(data)

2.G[ ]:list forG-mean

3. predict[ ]:list fory_predict

4.foriinit tolen(zong_ls) byincrdo

5.ls_bian[ ]:list for Boundary domain

6.ls_fu[ ]:list for Negative domain

7.ls_zheng[ ]:list for Positive domain

8.forcinit tozong_ls[i] byincrdo

9.p=len(list(set(len(zong_ls)).intersection(set(c))))/len(c);

10.ifp≥0.75then

11.ls_zheng←c

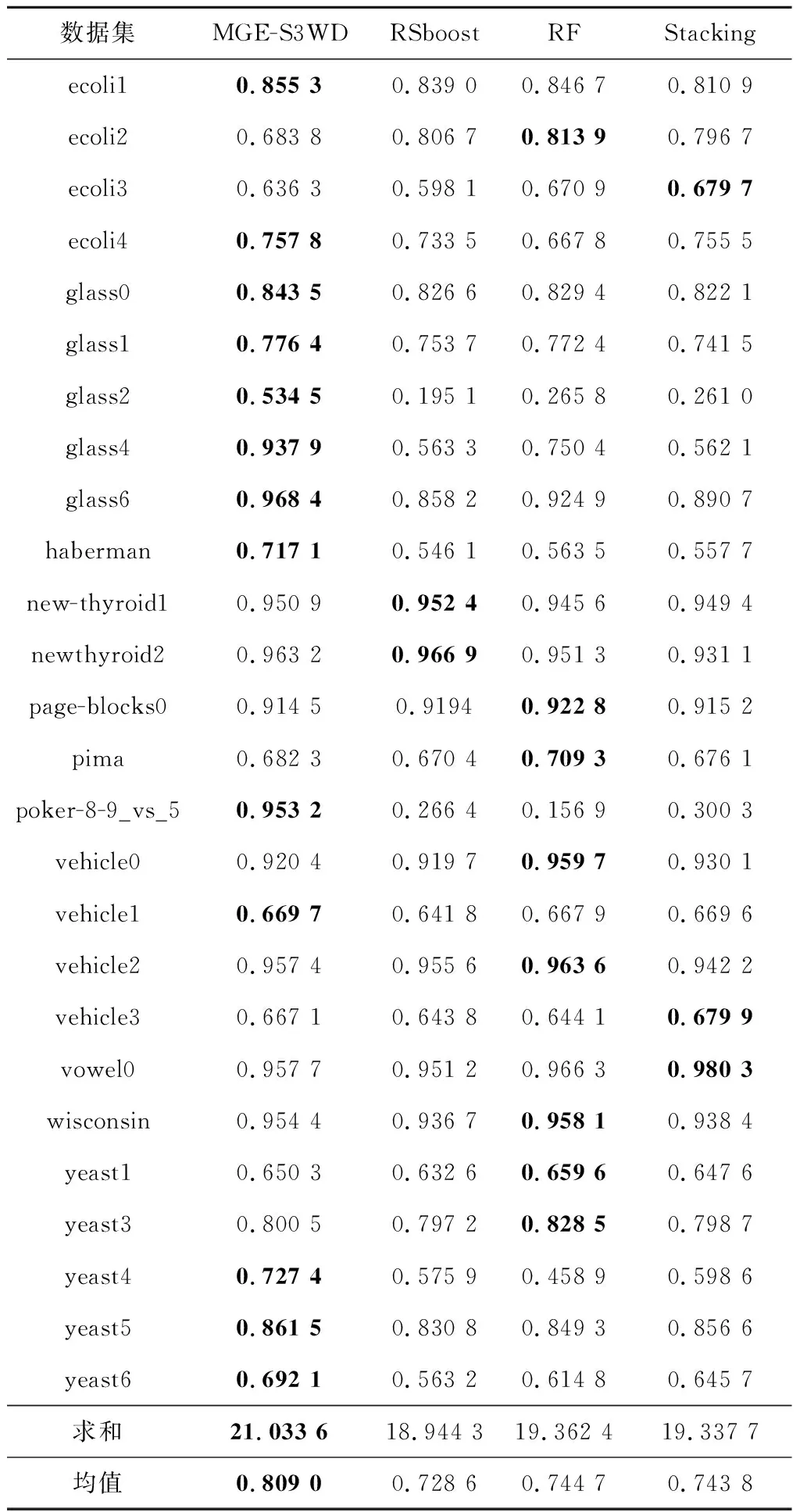
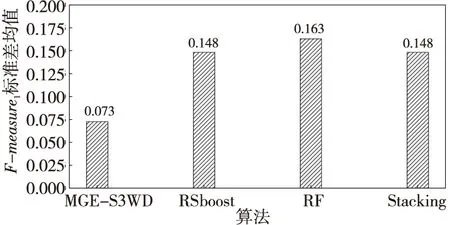
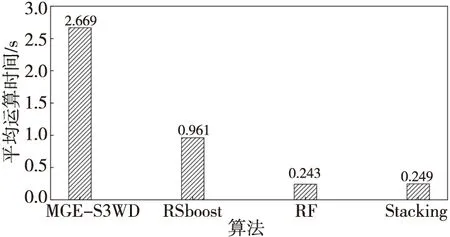
12.elif0.4

13.ls_bian←c

14.else

15.ls_fu←c

16.endfor

17.clf=DecisionTreeClassifier(criterion='gini');

18.ifclf.score>0.5then

19.predict←y_predict

20.endfor

21.returnpredict

3.2 模型构建

在不同粒层空间的训练子集Di上构建CART决策树，训练基分类器。分类模型构造过程如下所示：

步骤1数据动态划分。利用二元关系动态划分数据集，构建序贯三支决策粒化算法，科学地粒化数据集，获得不同的粒层空间Ω0,Ω1,…,Ωn。

步骤2融合数据子集。将粒层空间上划分形成的数据子集按照正域与边界域、正域与负域、边界域与负域融合数据，形成数据子集Di。

步骤3构建分类模型。以粒层空间中形成的数据子集Di作为模型的训练数据集，构建CART决策树。根据式(13)计算数据子集Di的基尼系数，如果基尼系数小于阈值，则返回决策子树，当前节点停止递归。

在分类问题中，数据集中类别数目为m，样本p属于第i类的概率为Pi，则该样本的基尼系数为：

(13)

样本集S′的基尼系数为：

(14)

其中，|S′|表示集合S′的总样本数，|Di|表示集合S′中属于第i类的样本数。基尼指数表示集合S′的不确定性。

计算当前节点各特征值对数据子集Di的基尼系数。

选择基尼系数最小的特征A和对应的特征值a。根据最优特征和最优特征值，将数据子集划分为2部分，同时建立当前节点的左右节点，对左右子节点递归生成决策树。

4 仿真实验与性能分析

4.1 数据集和仿真环境

基于Python实现算法仿真。系统环境：CPU：Intel i5-6500；RAM：8 GB；操作系统：Windows 10 专业版；解释器：Python 3.7。

MGE-S3WD算法主要使用KEEL不平衡数据库中的26组数据集进行仿真实验，数据集基本信息如表2所示。表2中不平衡比IR(Imbalance Ratio)表示多数类样本与少数类样本数量的比值。实验过程中，所有数据集均按照训练集80%，测试集20%的比例随机划分。

4.2 性能分析

MGE-S3WD算法以CART决策树作为分类工具，构建分类模型，并与文献[8]中的随机子空间集成分类算法(RSboost)、随机森林算法(RF)、Stacking集成框架下的分类算法进行对比实验，RSboost分类算法采用文献[8]中给出的运算过程及默认参数，而随机森林算法和Stacking集成分类算法均采用默认参数。

仿真过程中，采用五折交叉验证的方式以G-mean和F-measure12个指标的均值作为算法最终分类得分，验证算法的分类性能，通过2个评价指标的标准差验证算法的稳定性，算法的G-mean值如表3所示，最优结果均以加粗的形式在表格中标出。

Table 2 Data sets basic information表2 数据集基本信息

分析表3中各分类算法的G-mean值可以看出，MGE-S3WD算法在ecoli1、ecoli4、glass0、glass1、glass2、glass4、glass6、haberman、poker-8-9_vs_5、vehicle1、yeast4、yeast5、yeast6 13个数据集上的分类精度明显优于其他3种集成分类算法，在不平衡比较高的数据集上，MGE-S3WD能取得更高的分类精度。在new-thyroid1、newthyroid2 2个数据集上，RSboost集成分类算法优于其他算法；在ecoli3、vehicle3、vowel0 3个数据集上，基于Stacking集成的分类算法优于其他算法；在ecoli2、page-blocks0、pima、vehicle0、vehicle2、wisconsin、yeast1、yeast3 8个数据集上，随机森林算法优

Table 3 Classification G-mean of each algorithm表3 各算法分类G-mean值

于其他算法，而MGE-S3WD是次优的分类算法。在高度不平衡数据集中，少数类样本数量有限，传统集成框架下的分类算法学习少数类样本的信息量较少，导致分类精度偏低，分析算法的分类结果可以发现，MGE-S3WD更擅长高度不平衡数据的分类问题。

标准差是衡量算法稳定性的重要指标，标准差越低则算法的稳定性越好，反之稳定性越差。通过图2中各数据集上标准差均值可以看出，本文算法在不平衡数据集上的整体稳定性明显优于其他3类集成分类算法。

Figure 2 Classification G-mean standard deviation of each algorithm图2 各算法分类G-mean标准差均值

F-measure1是衡量不平衡数据分类算法性能的重要指标，与G-mean值不同的是，F-measure1指准确率(P)与召回率(R)之间的关系，从式(15)可以看出，准确率与召回率是两组互相矛盾的指标，当准确率较高时，F-measure1值有可能偏低。

(15)

准确率P=TP/(TP+FP)，召回率R=TP/(TP+FN)，其中TP为少数类样本正确分类的样本数目，FN为少数类样本错误分类的样本数目，TN为多数类样本正确分类的样本数目，FP为多数类样本错误分类的样本数目。

分析表4中各分类算法的F-measure1值可以看出，在glass1、glass2、glass4、haberman、new-thyroid1、newthyroid2、poker-8-9_vs_5、vehicle1、yeast4、yeast5 10个数据集上，MGE-S3WD的F-measure1值优于其他3种集成分类算法；而其他数据集上不同集成分类算法各有优势，对比各类算法的G-mean值可以看出，在部分数据集上，当G-mean值较高时，F-measure1值偏低。

通过分析图3中各分类算法的F-measure1值标准差均值可以得出，在F-measure1评价指标下，MGE-S3WD算法的标准差明显优于其他3种集成分类算法，因此，从算法的稳定性而言，MGE-S3WD算法优于其他3类集成分类算法。

运算时间是评价算法运算效率的重要指标，时间越短，算法的计算效率越高，图4是各数据集上各算法的运算时间，单位为秒。分析图4中数据可以看出，RF的运算时间最短，其主要原因是，其余3种算法在数据预处理过程消耗的时间较长，而RF在预处理阶段只进行采样，不需要更多的计算，因此，RF的运算效率高于其他3种集成分类算法。虽然MGE-S3WD算法的计算时间长于其他分类算法，但该算法能够有效提升模型分类精度和稳定性，因此，牺牲少量运算效率提升模型的分类精度和稳定性是值得的。

Table 4 Classification F-measure1of each algorithm表4 各算法分类F-measure1值

Figure 3 Classification F-measure1 standard deviation of each algorithm图3 各算法分类F-measure1标准差

Figure 4 Classification operation time of each algorithm图4 各算法分类运算时间

综合分析各算法的G-mean、F-measure1及算法运算时间可以得出，MGE-S3WD在处理高度不平衡数据时，算法的分类精度和稳定性明显优于其他3种集成分类算法。但是，在部分不平衡比较低数据集上，该算法不能很好地划分正域、边界域和负域，导致集成学习的基分类器差异性较差，因此，从分类算法在各数据集上的总体分类精度而言，该算法低于随机森林算法(RF)2%左右。从稳定性而言，该算法的稳定性明显优于其他3种集成分类算法，因此，针对不平衡比较低的数据集，可以通过牺牲少量分类精度来提升模型的稳定性。如果需要较高F-measure1值，则建议选择随机森林算法，但随机森林算法的随机性较强，稳定性较差。如果需要较高的运算效率，建议选择RSboost集成分类算法，该算法在小规模数据集上，运算效率较高，随着数据集数据规模的增大，随机子空间划分时间越长，因此，当处理较大规模数据时，建议选择随机森林算法或Stacking集成分类算法。

5 结束语

不平衡数据的分类问题在数据挖掘领域备受关注，传统集成分类算法并未对数据进行有效的预处理，数据集不同的分布情况对集成分类算法精度影响较大。本文采用序贯三支决策的多粒度集成分类算法可以有效降低数据子集的不平衡比，提升基分类器差异性，避免分类模型过拟合。实验结果表明，该算法能够有效识别少数类样本，提升算法分类精度，尤其是针对高度不平衡数据提升效果更明显。该算法通过引入代价敏感序贯三支决策的思想对数据进行预处理，将各粒层空间划分为正域、边界域和负域，并将各区域有规律地组合，形成新的数据子集，提高了集成分类算法的分类精度和稳定性。该算法粒化时间较长，因此，如何提升运算效率是未来的研究方向。