一种非乱序存储的数据交织加固技术*

王丹宁,刘 胜,李振涛

(国防科技大学计算机学院，湖南 长沙 410073)

1 引言

在现在大多电子系统中，静态随机访问存储器SRAM(Static Random Access Memory)是必不可少的一部分，广泛应用于嵌入式专用集成电路中[1]，SRAM存储的可靠性对电子系统至关重要[2]。空间辐射环境中，高能粒子引起的存储电路中的单粒子翻转SEU(Single Event Upsets)是集成电路最常见的可靠性问题之一[3,4]。在深亚微米体系下，中子引发的软错误[5]甚至会导致多个物理相邻的存储元发生翻转，即MCU(Multiple Cell Upset)，严重时可能导致系统崩溃。通过观察发现，发生软错误的多个存储元大多是物理相近的[6]。为了减轻软错误带来的影响，多采用纠错码ECCs(Error Correction Codes)来对存储器进行加固[7 - 9]。人们发明了汉明码、循环码和卷积码等编码技术对存储器进行加固，但这些技术仅在检测和校正单个差错和不太长的差错串时才有效，当产生连续多个误码时，汉明码、循环码和卷积码就不能满足所需的纠错能力，于是有了交织技术的出现[10]。在对发送的数据进行编码后，通过交织将原来的顺序打乱写入存储器，这样当数据产生连续错误时，由于接收端要先进行解交织，连续错误就会被打散，有利于解码模块进行纠错[11]。针对汉明码、循环码和卷积码，在无突发干扰时，交织技术对3种典型的信道纠错编码性能影响不大；有突发干扰时，交织技术通过改造信道但不增加冗余，有效提高了3种典型的信道纠错编码性能[10]。因此，可通过在编码中融入交织来纠正连续多位错误，从而对存储进行加固。然而，交织也带来了存储信息乱序的问题。

针对交织带来的存储信息乱序这一问题，本文提出了一种非乱序存储的数据交织加固技术，通过改进原来的交织编解码问题，将交织融入编解码模块来解决存储信息乱序问题。最后的验证结果表明，该技术不但能充分利用交织的优势，纠正连续多位错误，还能保证存储数据顺序与原始数据顺序相同。

本文首先在第1节给出引言，然后在第2节提出当前交织编解码原理及其存在的问题，接着在第3节提出非乱序交织编解码设计过程，在第4节给出验证和评估分析结果，最后在第5节进行总结。

2 交织编解码原理

2.1 当前交织编解码原理

常用的交织方法有分组交织、卷积交织和随机交织[10]，本文主要依据分组交织。分组交织的原理是将待交织的输入数据均匀分成多个码字，码字表示进行过纠检错编码的数据，由数据位和校验位构成，以可以纠一检二的Hsiao码为例，m位码字形式如图1所示，由k位数据位和m-k位校验位组成。

假设要进行分组交织的数据能均匀分成n个m位码字，则该数据可构成一个m行n列的交织矩阵，如下所示：

其中，n为交织深度，m为交织约束长度或宽度。交织的过程为按列写入，按行读出。待交织数据以1，2，…,m，m+1，m+2,…,2m,…,(n-1)m+1，(n-1)m+2，…,nm的顺序进入交织矩阵，再以1，m+1,…,(n-1)m+1，2,m+2，…,(n-1)m+2，…,m，2m，…,nm的顺序从交织矩阵中读出，这样就完成了对nm个输入数据的交织深度为n、交织约束宽度为m的分组交织。作为交织过程的逆过程，解交织的过程为按行写入，按列读出，待解交织的数据以1，m+1,…,(n-1)m+1，2,m+2，…,(n-1)m+2，…,m，2m，…,nm的顺序进入交织矩阵，再以1，2，…,m，m+1，m+2,…,2m,…,(n-1)m+1，(n-1)m+2，…,nm的顺序从m行n列的交织矩阵中读出，这样就完成了逆交织，恢复成为交织前的数据。

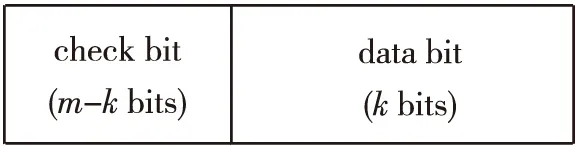
Figure 1 Codeword form图1 码字形式

利用交织对存储进行加固的主要过程如图2所示，当需要将数据写入存储器时，先将待写入存储器的数据分组，并对每组数据用编码模块进行纠检错编码，如纠一检二码、纠一检二纠相邻码等；然后以分组数作为交织深度、编码后的数据位数作为交织

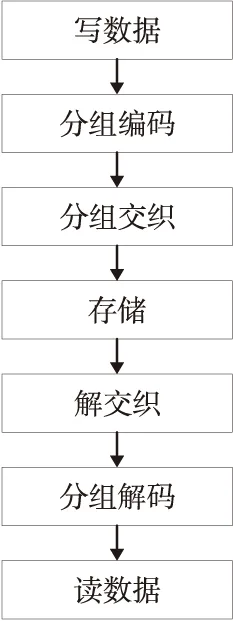
Figure 2 Interleaving process with encoding and decoding图2 交织编解码过程

约束宽度对编码后的数据进行交织，每组码字为交织矩阵的一列，将交织结果写入存储器。当从存储器读出存储字后，将其按行写入交织矩阵进行解交织，然后分组进行解码，输出解码结果。

编码模块如图3所示。

Figure 3 Encoding module图3 编码模块

解码模块如图4所示，其中，可纠错误类型表示错误为可以纠正的错误，解码后的数据为正确的数据，可纠错误比特位置表示当错误为可纠错类型时的出错比特位置，不可纠错误类型表示错误不可被纠正。

Figure 4 Decoding module图4 解码模块

若数据有24位，要通过交织编解码来对存储进行加固，若编码模块可对6位数据进行纠一检二编码，校验位数为2位，则可将原数据分成4组，每组数据位数为6位分别进行编码，编码后每组数据为8位，共32位。然后对编码后数据进行深度为4、约束宽度为8的交织后写入存储器。这32位数据可表示如式(1)所示：

X=(x0,x1,x2,x3，…,x29,x30,x31)

(1)

交织时，将X按列写入如下所示的8*4的交织矩阵中：

按行读出的交织结果为：

X′=(x0,x8,x16,x24,…,x15,x23,x31)

(2)

将交织结果X′存入存储器中。若此时产生一个连续4位错误，错误位的下标分别为0,8,16,24，使得存储信息变为X″，表示为：

(3)

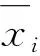
在进行读操作时，将其从存储器读出后，先进行解交织，即将其按行写入如下所示的8*4的交织矩阵中：

(4)

可见，经过交织矩阵与解交织矩阵的变换后，原来X′的连续4位错，就变成了X″中的随机独立差错，通过每8位进行纠一检二的纠错，可以分别将4位错纠正。所以，交织结合纠检错编码可以纠正连续多位错。

2.2 当前交织编解码存在的问题

从2.1节的交织编码例子可以看出，由于进行了交织，当交织结果存入存储器后，存储信息是乱序存放的，也就是说，当前用交织编解码进行存储加固存在存储数据乱序问题。这虽然对芯片本身不构成影响，但在进行硬件调试时，数据信息乱序会给硬件调试时的数据访问带来不便，进而影响硬件调试，降低硬件调试效率。所以，将存储信息调整为正确的顺序是有必要的。为了既能发挥交织地纠正连续多位错的优势，又能确保存储信息的正常顺序，本文设计了一种非乱序存储的数据交织加固技术。

3 非乱序交织编解码设计

3.1 非乱序交织编解码过程

本文对交织编解码过程进行了改进，提出非乱序交织编解码过程，如图5所示，同之前的交织编解码过程相比，本交织编解码过程将交织融入编解码过程，提出非乱序交织编码和非乱序交织解码。

Figure 5 Non-out-of-order interleaving encoding and decoding process图5 非乱序交织编解码过程

3.2 非乱序交织编码模块和非乱序交织解码模块

通过对原交织编解码过程进行分析不难看出，导致存储数据乱序的主要原因是交织，若要让数据恢复成正常的顺序，就需对其解交织。所以，可以在将数据存入存储器前，对其进行一次交织和一次解交织操作，使得存入存储器的数据顺序不发生改变。于是，本文提出了非乱序交织编码模块，将原先的编码模块与交织融合到一起，采用逆交织、编码、交织的方法来保证存入存储器的数据为正常的顺序。非乱序交织编码模块如图6所示。

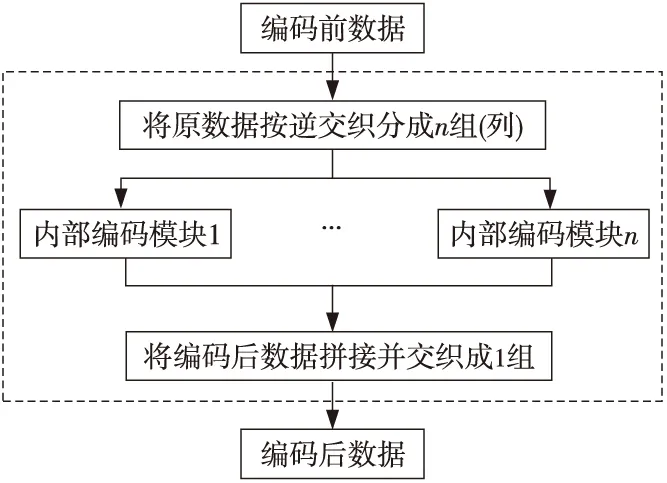
Figure 6 Non-out-of-order interleaving encoding module图6 非乱序交织编码模块

图6中，虚线框表示将编码与交织进行封装，框内整体作为非乱序交织编码模块，框外为模块的输入输出，后面的非乱序交织解码模块同理。

如图6所示，在数据存入存储器前，先对其进行逆交织，按行写入交织矩阵；然后读出的每一列作为一组，对每组分别进行纠检错编码，如纠一检二、纠一检二纠相邻等；然后将编码后的数据进行拼接，再进行交织，最后将交织结果存入存储器。解交织和交织的交织深度相同，根据输入数据位数d和内部编码模块输入的数据位数s来确定交织深度n，确定方法为：n=d/s，交织约束宽度不同，解交织约束宽度为m=d/n，交织约束宽度为m=s+r，r为内部编码模块输入的数据位数为s时的校验位数。

作为编码模块的逆过程，非乱序交织解码模块将解码过程与交织融合，采用交织、解码、逆交织的顺序，就可以对读出的数据进行解码纠错。非乱序交织解码模块如图7所示。

LMPP方法根据功能函数的非线性程度及目标可靠度确定局部采样区域的大小，但由于未能考虑Kriging近似的误差，导致局部采样区域过小而遗漏某些重要样本点。如图3所示，f(x)为真实的功能函数约束边界，为由克里金近似拟合出来的约束函数边界。外边的圆圈是本文提出的局部采样区域，里面的圆圈是LMPP方法的局部采样区域。可以看出，利用LMPP方法进行采样时，由于未能充分考虑克里金近似的误差，导致对真实的功能函数约束边界f(x)影响较大的样本点A未被采样，降低了采样效率。为提升LMPP方法的采样效率，本文在功能函数非线性程度及目标可靠度的基础上，进一步考虑Kriging近似的误差，计算模型如下：

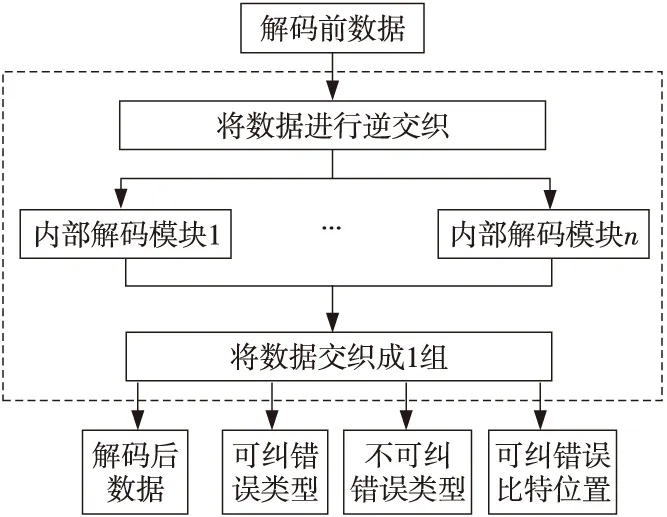
Figure 7 Non-out-of-order interleaving decoding module图7 非乱序交织解码模块

若待写入存储的数据Y为32位，进行深度为4的交织，则图6中的每个编码模块需要对8位数据进行编码，假设进行纠一检二编码，每8位数据需要5位校验位。待写入存储器的数据Y可表示如式(5)所示：

Y=(y0,y1,y2,…,y29,y30,y31)

(5)

对数据Y进行交织深度为4、交织约束宽度为8的逆交织，即将其按行写入如下所示的8*4的交织矩阵中：

按列读出时，每一列数据为一组，分别进入内部编码模块进行编码，每列数据加上如下所示的校验位的编码结果：

其中，r1～r5表示交织矩阵第1列的8位数的校验位，其它3列以此类推。

在编码后进行交织，交织矩阵深度仍为4，但交织约束宽度变为8+5=13，13*4的交织矩阵如下所示：

按行读出交织结果Y′如式(6)所示：

Y′=(y0,y1,y2,…,r1,r6,…,r15,r20)

(6)

将交织结果Y′存入存储器中。可以看出，此时存入存储器的数据位的顺序同待写入存储器的数据相同。假设在存储器中产生连续的4位错误，其下标为0,1,2,3，使得存储信息变为Y″，可表示成式(7)所示：

(7)

将Y″从存储器读出后进行交织深度为4、交织约束宽度为13的逆交织，交织矩阵如下所示：

按列读出逆交织结果Y‴如式(8)所示：

(8)

每一列为一组，对每组数据进行纠一检二解码，由于每组均产生了1位错，为可纠错类型，用4个解码模块对各列进行解码，4个错误均可以得到纠正，所以解码后的没有校验位的数据Y″″如式(9)所示：

Y″″=(y0,y4,…,y24,y28,y1,y5,…,y25,y29,

y2,y6,…,y26,y30,y3,y7,…,y27,y31)

(9)

对解码后的数据进行交织深度为4、交织约束宽度为8的交织，交织矩阵如下所示：

按行读出的交织结果Y″″′如式(10)所示。

Y″″′=(y0,y1,y2,…,y29,y30,y31)

(10)

由于错误得到纠正，所以Y″″′=Y。

可见，经过交织矩阵与解交织矩阵的变换后，原来X′的连续4位错也得到了纠正，而且存储器的数据信息也没有乱序。所以，非乱序交织编解码过程既能发挥交织地纠正连续多位错的优势，又能确保存储信息的正常顺序。

4 验证和评估分析

4.1 验证平台的搭建

本节基于验证需求，搭建了一个层次化且高效的验证平台。此验证平台中包含随机激励、约束、黄金模型和断言表达式等，目的是实现自动产生带约束的激励与自动地进行比对验证。

本文基于某商业公司的RTL模拟环境来进行验证，验证程序用SystemVerilog编写。本次验证的原始数据位数为32位，交织深度为4，每8位数据位需要5位校验位，共需要4*5=20位校验位。验证平台的搭建主要有以下2个方面：

(1)定义功能点和激励：验证纠错后的数据和参考模型中正确的数据是否一致。由于验证中的激励主要是不断地在不同地址的数据中的不同位置加入连续多位错，激励类型比较单一，所以本次测试用例由加过约束条件后的rand类型变量自动产生，提高了效率。在进行功能点验证时，由5个rand类型变量来控制错误的插入，rand类型变量is_add_err表示是否要插入错误，rand类型变量whichbit_1、whichbit_2、whichbit_3和whichbit_4分别表示是否给连续4位错的第1/2/3/4位插入错误。因此，会有如下几种出错情况：无错以及有1/2/3/4位错，然后每次通过比较存储器返回数据与黄金存储模型golden_ram中的数据是否一致来确定错误是否得到纠正。

(2)验证平台的搭建如图8所示，待测设计DUT(Design Under Test)的周围即为验证平台，验证平台将生成的激励添加给待测设计，同时捕捉待测设计的响应。主要步骤如下：定义激励;将激励添加到待测设计;捕捉待测设计的响应;检查结果是否正确。

Figure 8 Schematic diagram of verification platform and design under test图8 验证平台与待测设计示意图

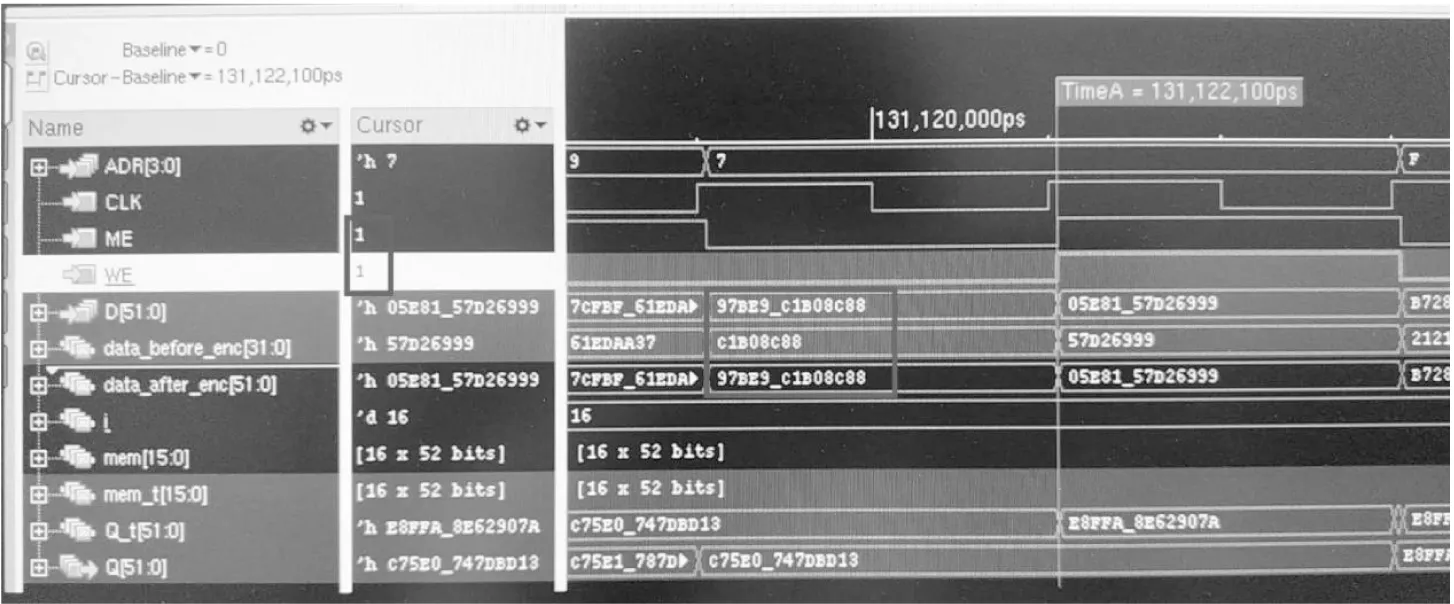
Figure 9 Comparison of data before non-out-of-order interleaving encoding and when storing in memory图9 非乱序交织编码前与存入存储器时的数据比较

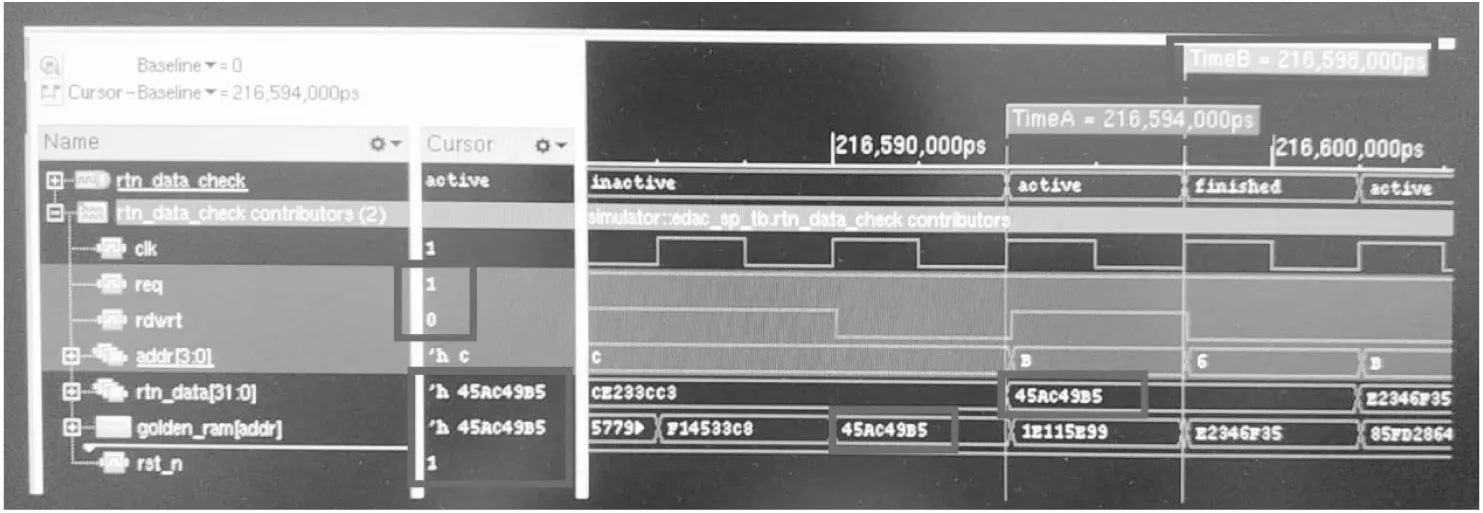
Figure 10 Function point verification图10 功能点验证

4.2 验证结果

非乱序交织编码前与存入存储器时的数据比较的仿真波形如图9所示。由图9可知，在TimeA=131120000 ps时，存储使能ME(Memory Enable)和存储写使能WE(Write Enable)均有效，此时，非乱序交织编码前的数据data_before_enc为0xc1b08c88，非乱序交织编码后的数据data_after_enc为0x97be9c1b08c88，待写入存储器的数据D为0x97be9c1b08c88。从数据对比可以看出，非乱序交织编解码前后的数据顺序没有发生改变，从而写入存储器的数据顺序也没有发生改变。

功能点的验证仿真波形如图10所示。从图10中可以看出TimeA和TimeB都处于时钟上升沿，TimeB比TimeA快了1个时钟周期即快了1拍，用TimeB= 216598000 ps为基准表示当前时刻，用TimeA表示前一拍。断言在时钟上升沿需满足：(req&&!rdwrt)|=>(rtn_data==$past(golden_ram[addr],1))；由上式可知，此时|=>的左边，req=1，rdwrt=0，所以满足先行算子表达式；而|=>的右边，在TimeB时刻rtn_data=0x45ac49b5，$past(,1)表示前一拍，而此时addr=0xc，golden_ram[0xc]前一拍的值即TimeA时刻的值也等于0x45ac49b5。所以，此时rtn_data== $past(golden_ram[addr],1)成立，即后续算子表达式成立，至此整个断言表达式成立，因此功能点的断言成功，验证完成。

由验证结果可知，一方面，非乱序交织编解码前后的数据顺序没有发生改变，从而写入存储器的数据顺序也没有发生改变；另一方面，验证纠错后的数据和参考模型中正确的数据一致。因此，非乱序交织编解码过程既能发挥交织地纠正连续多位错的优势，又能确保数据顺序不被打乱。与原交织编解码相比，非乱序交织编解码仅增加了1次交织和1次解交织。

5 结束语

存储加固引入交织可提高存储可靠性，交织会带来存储数据信息乱序的问题，进而影响硬件调试时的数据访问，降低硬件调试效率。本文提出一种非乱序存储的数据交织加固技术，通过对原交织编解码过程、编解码模块进行改进，提出了非乱序交织编解码过程和非乱序交织编解码模块，不但能充分利用交织的优势，还可将存储数据转换成非乱序。