基于十字梁结构的石墨烯高压压力传感器设计

薛 伟，侯 文，王俊强，齐 越，严赛美

(1.中北大学信息与通信工程学院，山西太原 030051；2.中北大学前沿交叉科学研究院，山西太原 030051；3.中北大学仪器与电子学院，山西太原 030051)

0 引言

高压压力传感器广泛应用于高压领域的压力测量。现有的高压压力传感器敏感元件普遍采用硅、碳化硅薄膜，由于硅和碳化硅的物理性能有限，传感器量程多为10～100 MPa，无法满足更大压力的测试需求[1]。石墨烯以其特有的力学、热学、电学、光学性质以及超高的稳定性成为制作高压、高温、高频器件的良好材料，在微电子、光电子等领域起到了独特的作用，成为国际上新材料、微电子和光电子领域研究的热点[2-6]。石墨烯具有高的杨氏模量[7]、高的断裂强度[8]，高热导率[6]和电子迁移率[9]，这表明石墨烯在高压环境下不易遭到破坏，且在小变形挠动下具有很好的压阻效应，基于石墨烯这些优点，国内外在石墨烯压力传感器理论研究、仿真模拟与实验方面取得了一些进展。在国外，2007年，J. S. Bunch等通过将石墨烯薄膜覆盖在一个空腔上，创造了第一个石墨烯压力传感器原型[10]；2012年，A. D. Simith等提出石墨烯压力传感器的结构与制造工艺，并对石墨烯的应变进行了分析[11];O. K. Kwon等通过增加圆柱形支腿的顶板改进了悬浮石墨烯压力传感器，在低压环境下灵敏度较高[12]。在国内，2011年，浙江大学的Y. Xu等提出了面内或隧穿石墨烯压力传感器[13]。在传感器结构设计方面，传统“C型”结构为提高灵敏度需要减小弹性膜的厚度，这会引起大挠度效应，使传感器线性误差增大[14]，不适于传感器在小变形挠动下发生压阻效应。“E”型结构能较大的减小中心挠度，使非线性减小，但石墨烯只能布置于单只梁根部，传感器可靠性降低。而采用“十字梁”结构能较大地增大中心挠度，并且石墨烯布置于4根支梁根部，增加了传感器的可靠性。本文通过COMSOL力学模块对石墨烯压力传感器芯片进行结构设计与灵敏度设计，设计制备了基于微电子机械系统(MEMS)工艺的压阻式压力传感器敏感芯片。

1 工作原理

被测压力作用于弹簧钢膜片使其产生形变，膜片下方的凸柱产生位移又作用于十字梁，使得转移在十字梁根部的石墨烯敏感膜片发生形变，如图1(a)所示，石墨烯原子间距随之发生变化，使得石墨烯的能带打开能隙，从而影响到石墨烯的电导率，惠斯登电桥随之失去平衡，如图1(b)所示，继而产生电学信号，通过检测电学信号并进行计算可获得传感器受到的压力大小。图1(b)中VCC为电桥供电电压，R为压敏电阻，ΔR为受到压力后变化的电阻阻值，U-和U+为电压输出端。

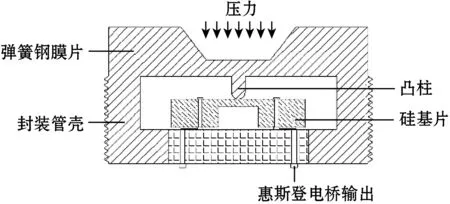
(a)传感器截面图

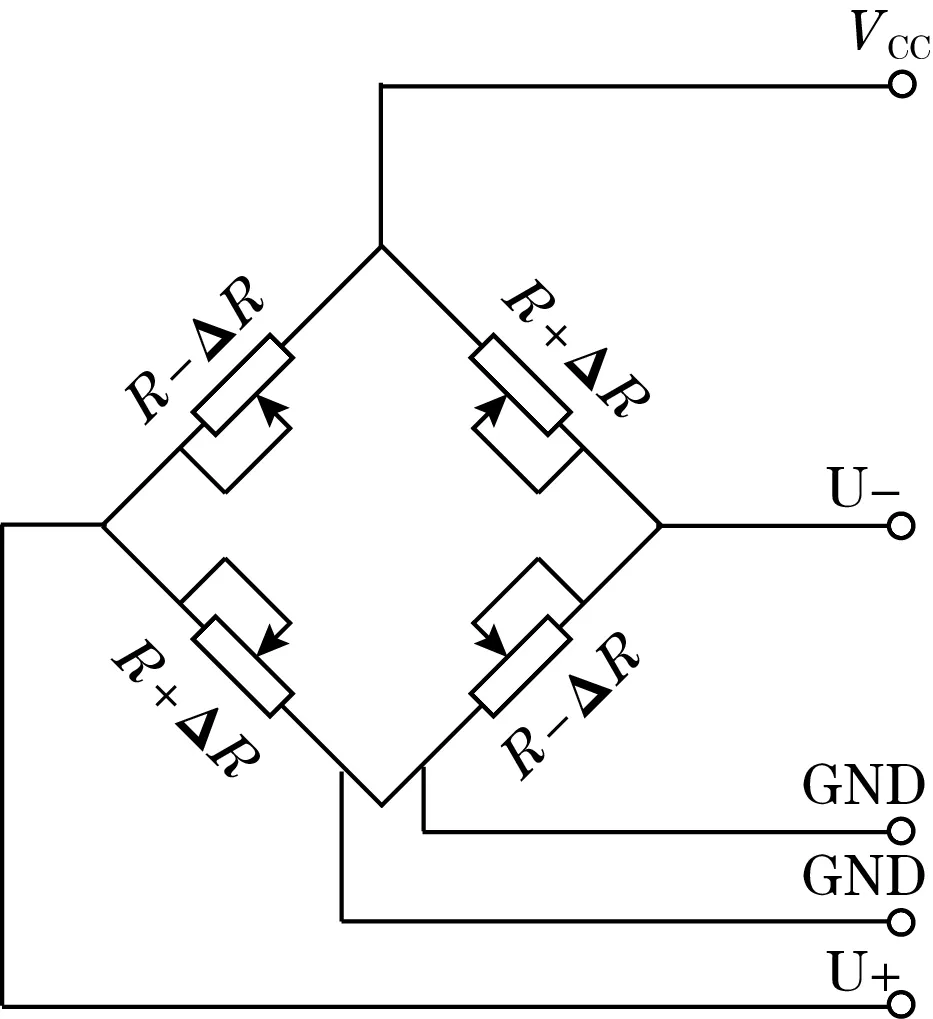
(b)惠斯登电桥图1 石墨烯高压压力传感器原理图

2 传感器结构设计

传感器自上而下依次为弹簧钢膜片(图2(a))、凸柱(图2(a))、硅基片(图2(b))。传感器目标量程为400 MPa，期望传感器封装后尺寸为10 mm×10 mm×10 mm，因此设计十字梁长宽为1 mm×0.15 mm，硅基片尺寸依据十字梁尺寸定为2 mm×2 mm×0.4 mm;设计弹簧钢膜片直径为8 mm。由COMSOL有限元仿真知，十字梁根部应变最明显，石墨烯敏感膜须转移至十字梁根部上表面，由十字梁振动带动石墨烯敏感膜表面应力变化，且考虑到石墨烯价格昂贵，为充分利用石墨烯有效性，因此我们设计单原子层石墨烯尺寸为0.15 mm×0.15 mm×0.35 nm。

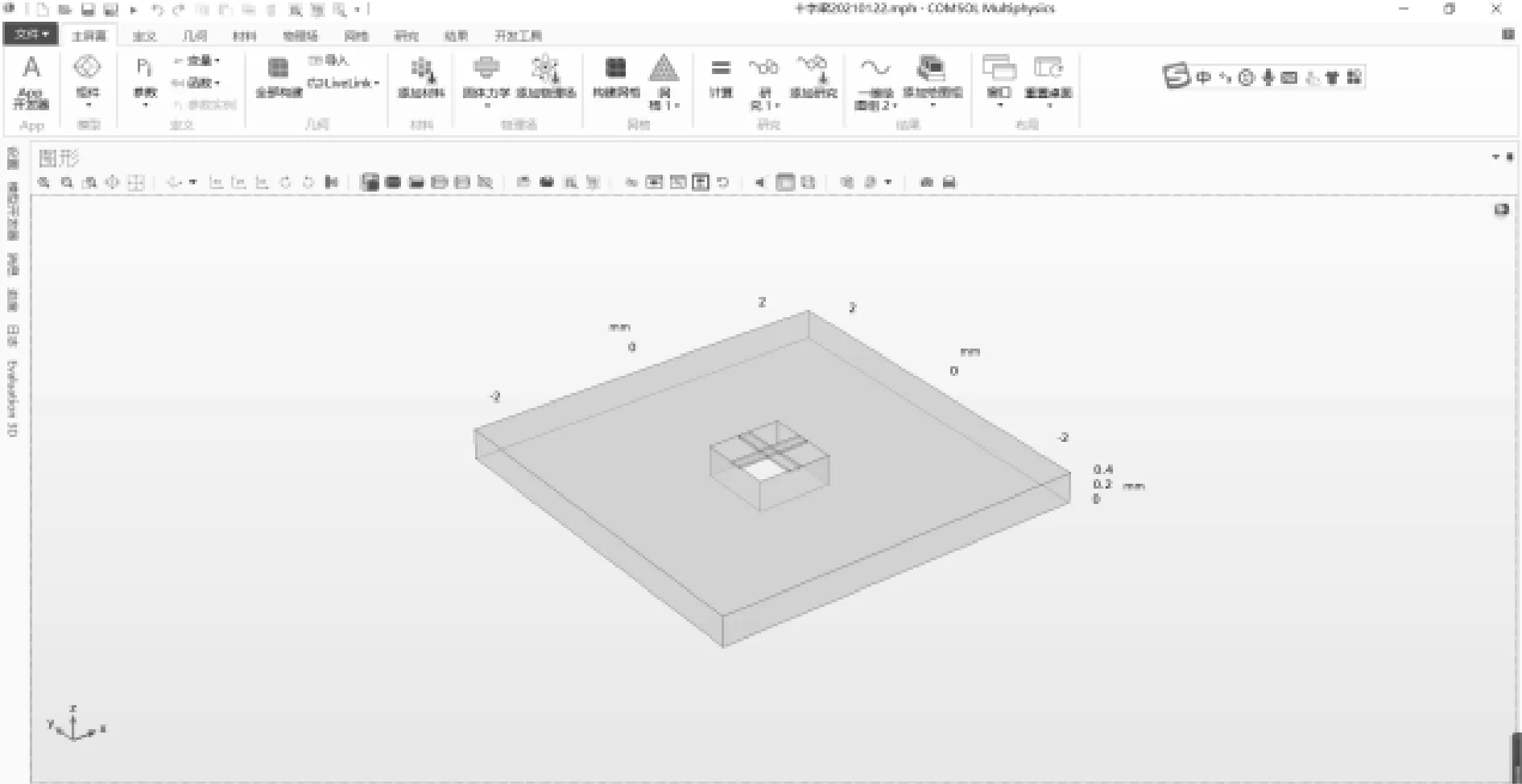
(a)弹簧钢膜片与凸柱

(b)硅基片

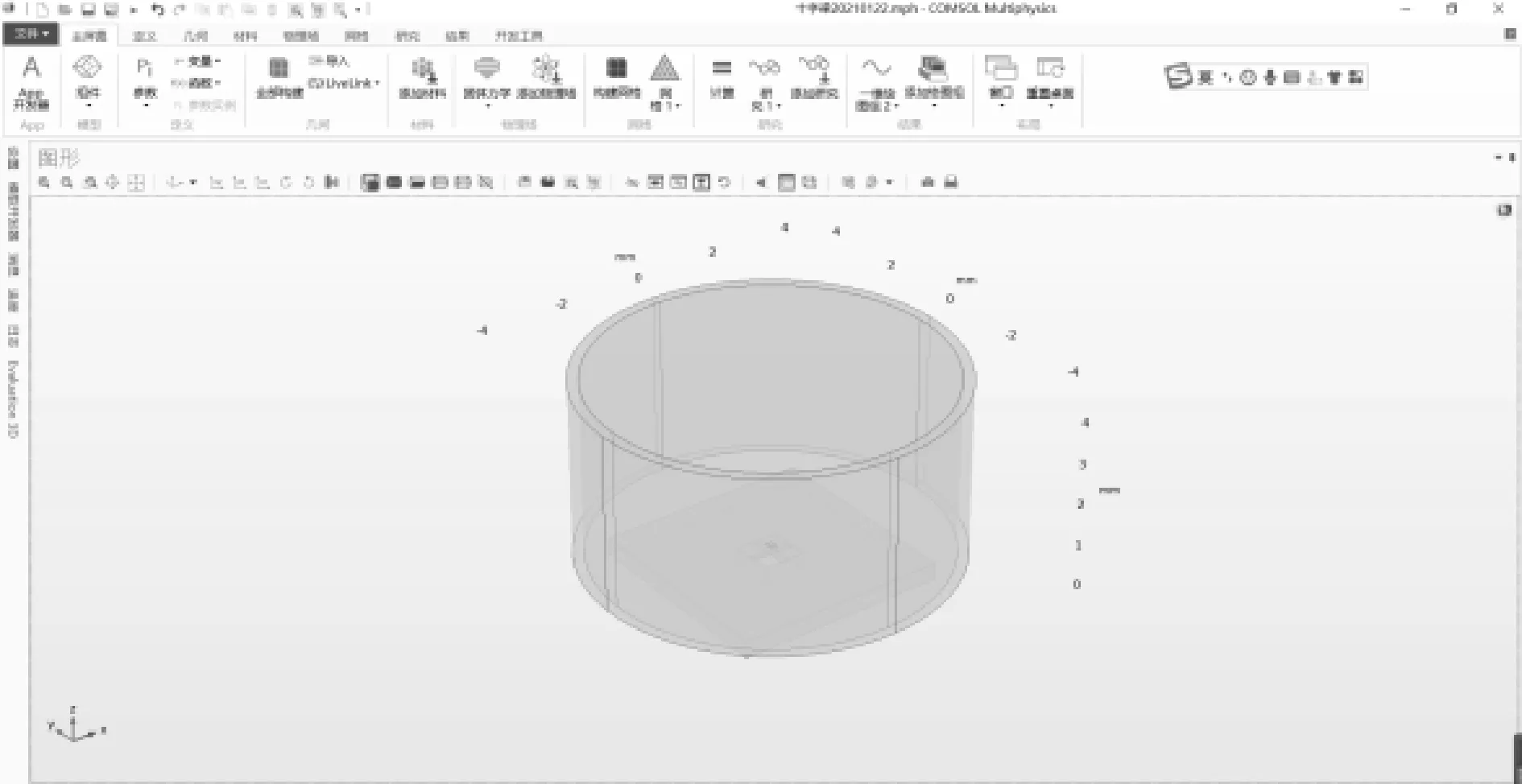
(c)传感器模型图2 压力传感器有限元模型

2.1 硅基片尺寸设计

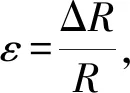
(1)

式中：E为弹性模量，E=190 GPa；σ为横向应力。

根据式(1)，通过COMSOL力学场对十字梁厚h1为30～80 μm的硅基片中心施加5～10 μm的位移并进行仿真分析。表1为不同梁厚下不同位移引起的最大应力。硅为各向异性材料，会表现出延展特性，发生塑性变形，故仿真中将硅设为各向异性弹塑性材料，Mises应力是判定材料是否进入塑性的一个综合指标，因此材料模型采用von Mises屈服准则。由仿真结果可知，在相同梁厚下，施加固定位移越大，硅基片承受的Mises应力越大;在相同位移下，十字梁越厚，Mises应力越大。

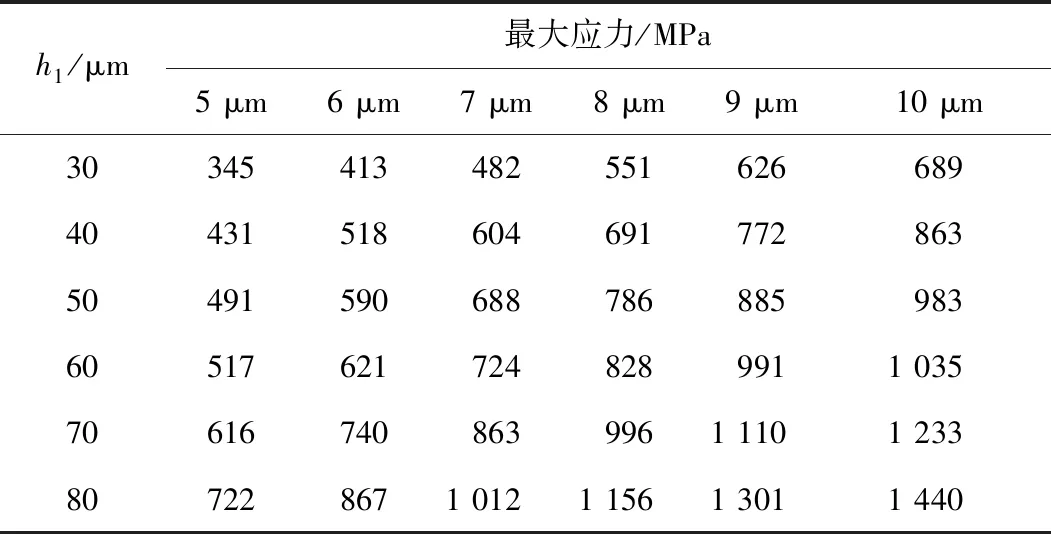
表1 不同梁厚下不同位移引起的最大应力

不同位移下十字梁厚度与应变关系如图3所示。

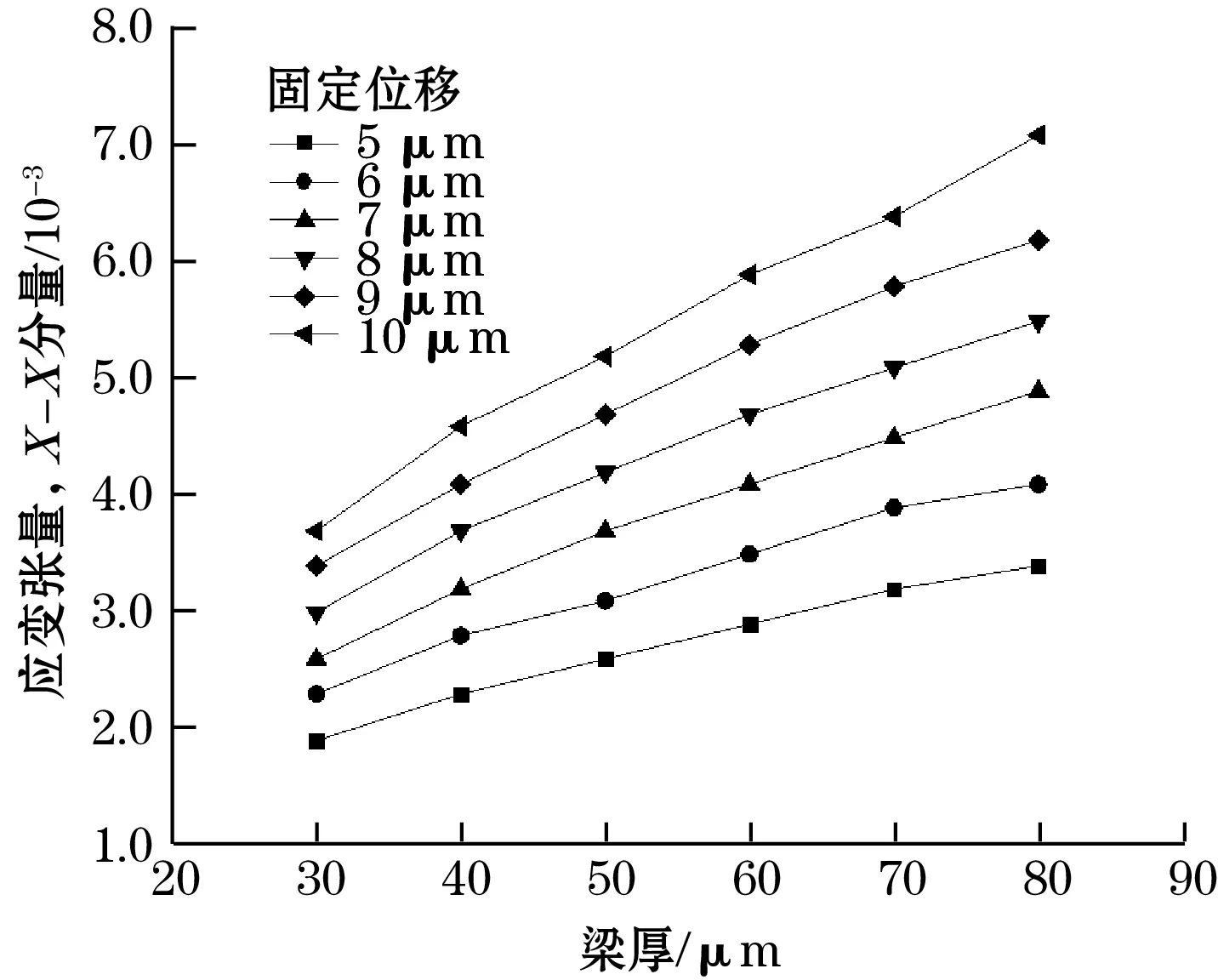
图3 中心处不同厚度下十字梁的厚度与应变关系

图3表明，施加相同固定位移，十字梁厚度越大，十字梁根部所承受的横向应变会随之变大;在相同梁厚下，固定位移越大，十字梁根部应变越大，石墨烯的横向应变越大。由于硅的屈服强度为7 000 MPa，而石墨烯只有应变大于0.2%时，石墨烯的电阻才会有明显变化[15-16]，当十字梁厚度为40 μm、施加固定位移为8 μm时，提取十字梁中线所受应力与X-X方向应变数据，结果表明承受压力为734 MPa，同时横向应变达到最大0.46%，仿真结果如图4所示。石墨烯敏感膜布置在距离十字梁根部0.011 mm处。

2.2 弹簧钢膜片尺寸设计

传感器钢膜片选用60Si2Mn弹簧钢，60Si2Mn弹簧钢具有耐腐蚀、耐高温高压、易加工等特性。表2为60Si2Mn 弹簧钢性能参数表。膜片形状采用圆柱形，根据设计要求，其直径a为8 mm，设计参数主要包括：弹簧钢膜承受的压力量程p，钢膜厚度h，钢膜中心挠度F，为保证压力p与钢膜产生的应力保持良好的线性关系，钢膜应符合薄板理论的小挠度变形原则，因此三者应满足以下公式[17-18]：

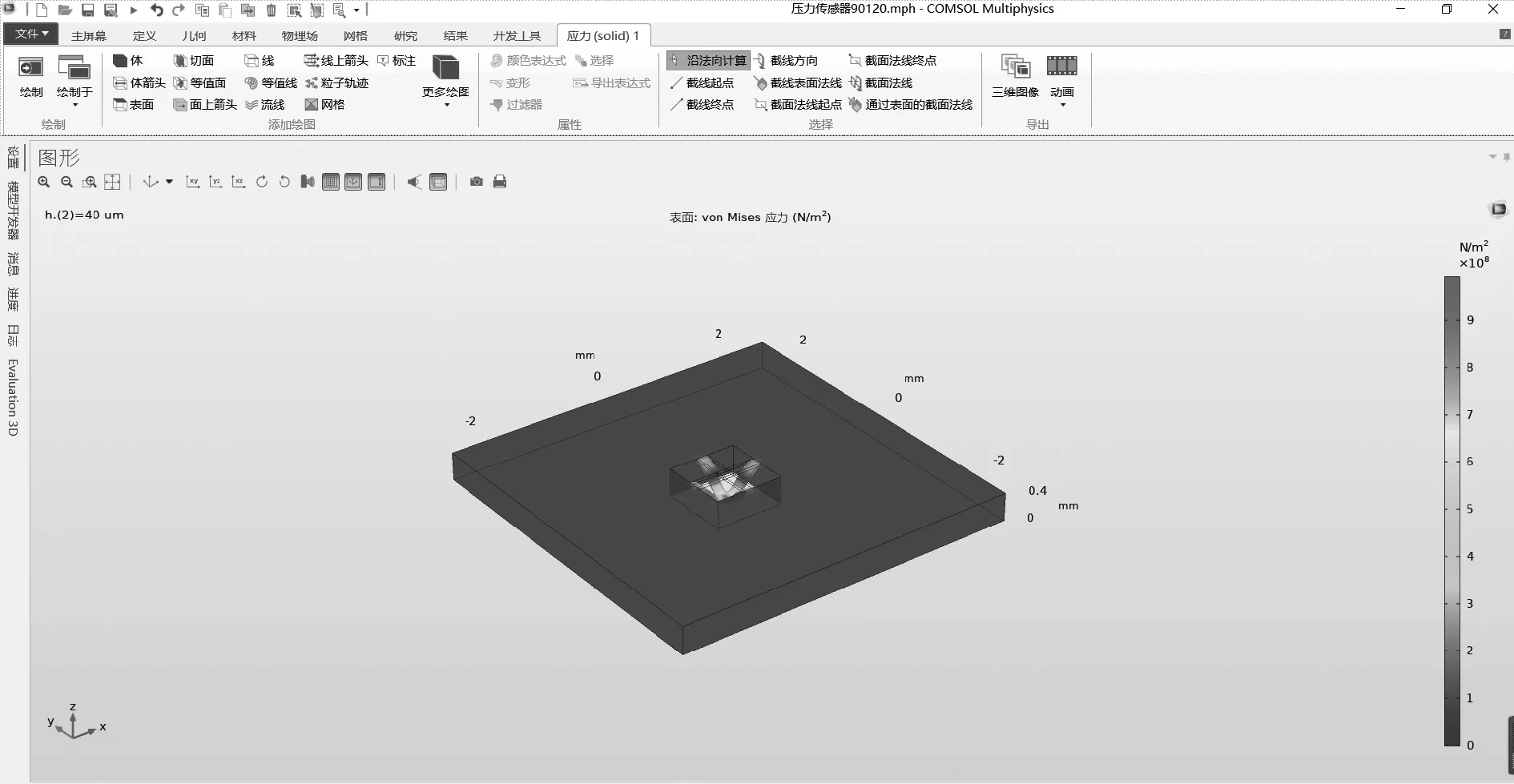
(a)压力分布云图

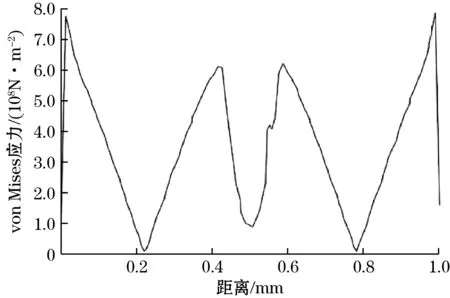
(b)十字梁中心von Mises应力与位置的关系

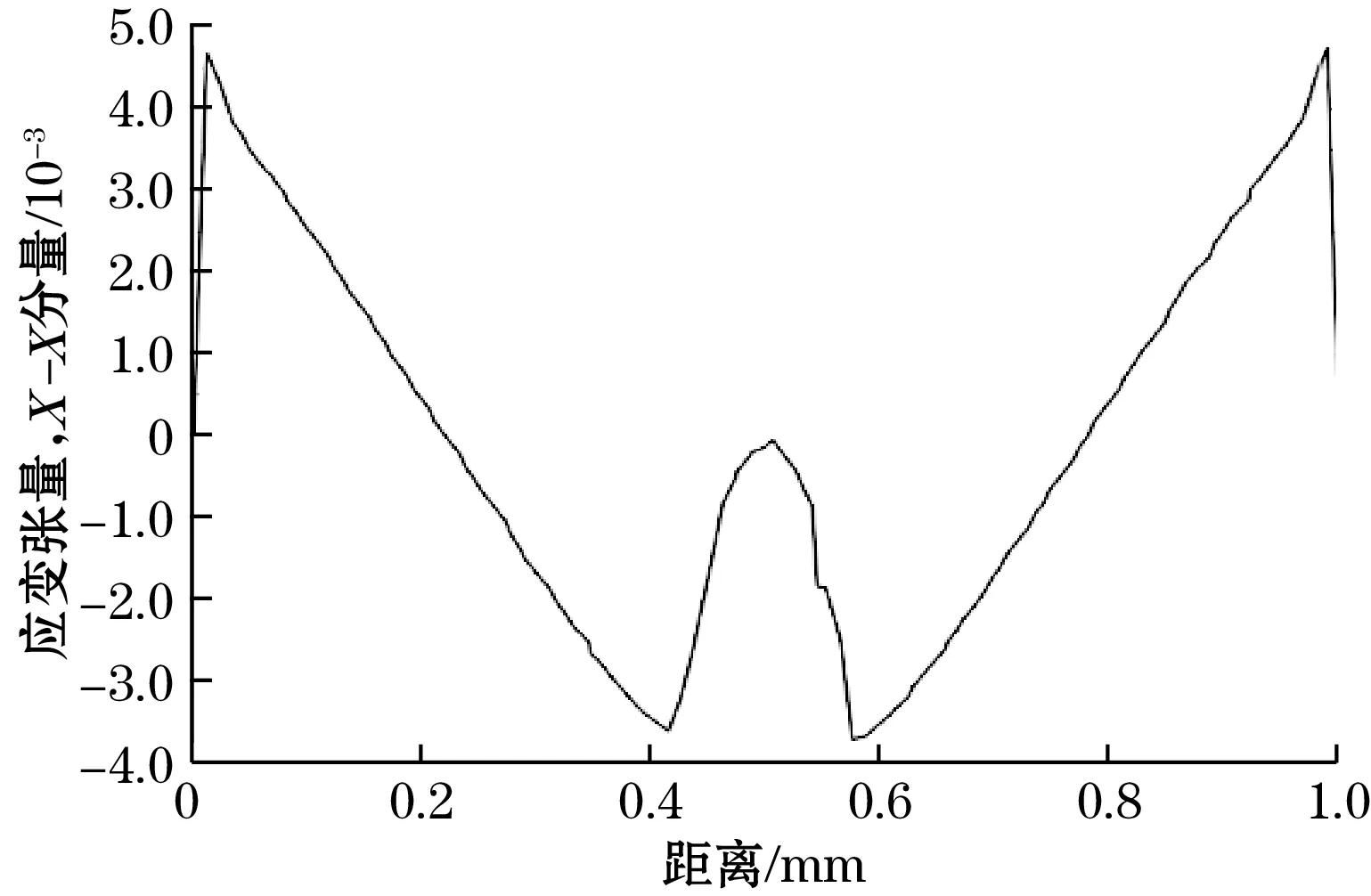
(c)十字梁中心X-X方向应变与位置的关系图4 十字梁中心仿真结构图

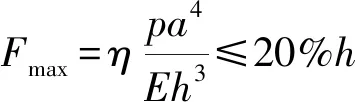
(2)

式中：Fmax为压力作用下的最大挠度;弹性模量E=206 GPa；泊松比为0.28时系数η=0.013 8;a为钢膜直径，h为钢膜厚度。

表2 60Si2Mn弹簧钢性能参数表

根据式(2)，通过COMSOL力学场对直径为8 mm、厚度4.0～4.4 mm的弹簧钢圆柱施加400 MPa压强并进行仿真分析。仿真结果如图5所示，图5中h为钢膜厚度。当钢膜厚度越大，钢膜承受的应力越小，中心位移越小。在均布载荷作用下，钢膜棱角处发生应力集中现象，需进行优化处理。

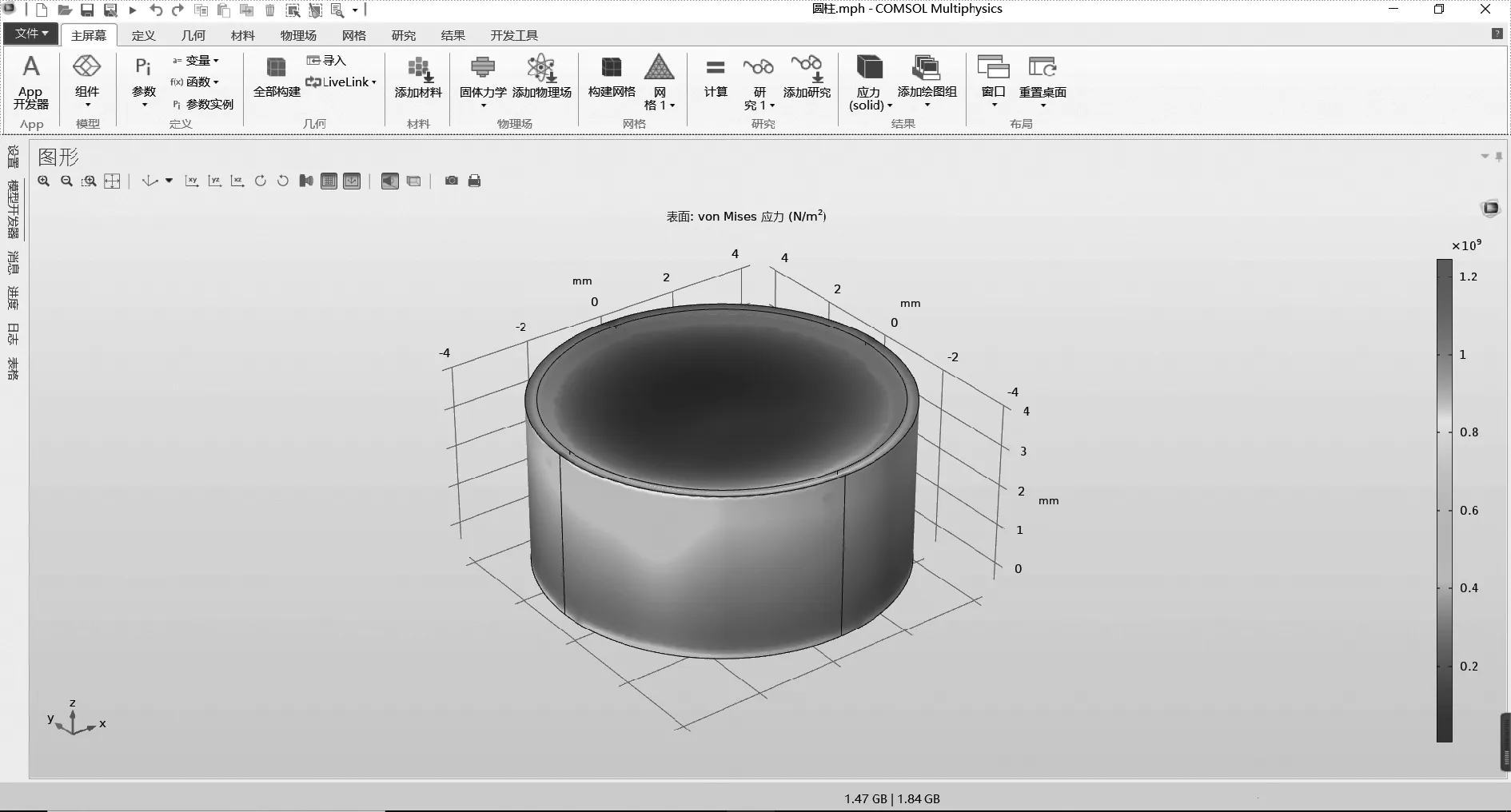
(a)压力分布云图

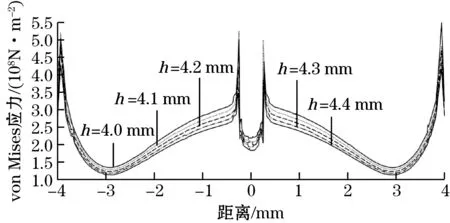
(b)钢膜中心von Mises应力与位置的对应

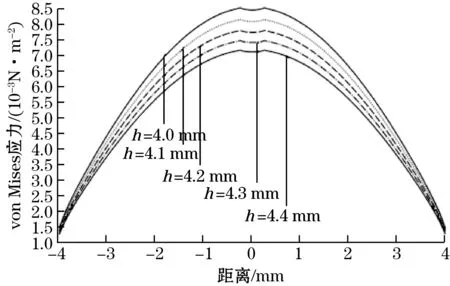
(c)钢膜中心位移与位置的对应图5 钢膜中心仿真结构图

由仿真结果可知，当弹簧钢膜厚度为4.2 mm时，钢膜中心位移达到7.9 μm，与十字梁所受应变最大值施加的固定位移8 μm接近，同时弹簧钢所承受最大应力为511 MPa，远未发生塑性变形。表3为不同钢膜厚度下引起的位移与应力表。

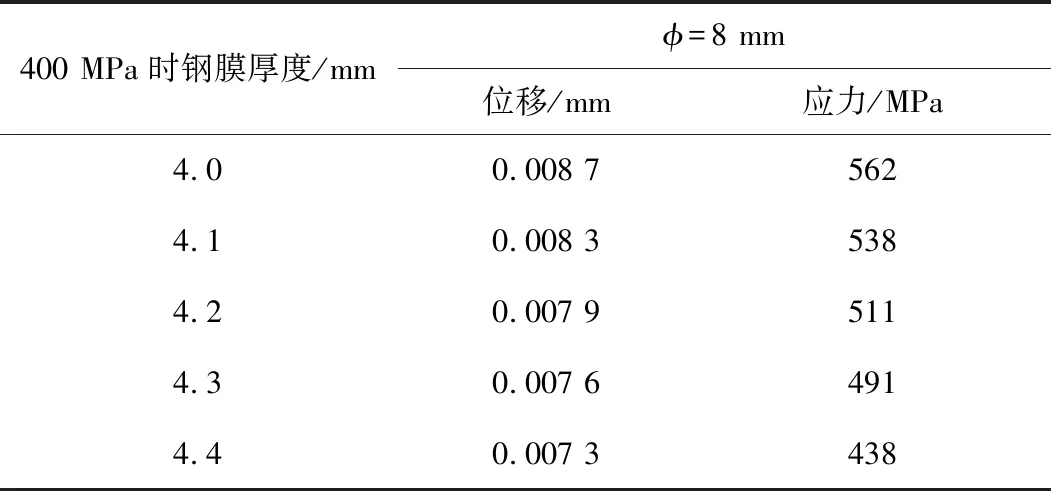
表3 不同钢膜厚度下引起的位移与应力表

最后，对硅基片与弹簧钢膜片组装的芯片结构进行六阶模态仿真分析，得到六阶频率结果如表4所示。

表4 六阶模态分析结果 kHz

一个物体的模态理论上具有无数阶的共振频率，但实际表现出来的现象是它们之间的叠加耦合，低阶贡献比高阶大的多，且阶数越低，贡献越大[19]，因此我们最关心的压力传感器模态是当沿着Z轴方向上的运动，即一阶振型的形变。我们设计的传感器一阶频率为223 kHz，同时一阶频率与二阶频率相差较大，说明一、二阶模态之间的耦合作用属于比较合理的范围内，符合该结构设计要求。

3 结论

本文建立了十字梁结构的压力传感器力学模型，并对传感器的硅基片和弹簧钢膜片进行了仿真分析，根据应变分布设计了石墨烯的分布位置。通过进行模态仿真分析，传感器一阶频率为223 kHz，符合结构设计要求。