基于lsqnonlin及遗传算法的涡扇发动机监测参数选择研究

吴君凤

(中国商用飞机有限责任公司上海飞机设计研究院,上海 201210)

发动机健康管理是航空发动机重要的组成部分，健康管理在增强飞机推进系统性能、可操作性、安全性和可靠性方面起着重要的作用[1]。故障诊断是健康管理很重要的组成部分，用到的技术主要有传感器技术、诊断技术与数据融合技术等[2]。传感器技术的运用是整个控制与健康管理的基础，传感器提供了一系列用于后续控制与决策的原始信息。

传感器监测参数的选择传统方法是部件研究人员与系统研究人员经反复协商后获得，且大多是定性结果，缺乏定量的结果。随着系统复杂程度增加和需求的不同，传统方法已不能满足要求。与传统方法不同，由NASA格林研究中心提出的系统化传感器选择策略(systematic sensor selection strategy，简称S4)，基于系统模型、系统诊断模型、健康信息等模块，依据公认的选择标准和性能指标来定量分析传感器在系统中的价值，并综合考虑成本、质量和可靠性等因素，针对不同目的，系统化、定量地选择最优的传感器集[3-7]。文献[3]研究了S4方法在火箭发动机中的应用；文献[4]概括了航天系统传统的传感器选择方法并研究了S4方法在航天系统中的应用；文献[5]和[6]研究了S4方法在民用涡扇发动机中的应用，并用C-MAPSS[7]进行仿真验证；文献[8]基于卡尔曼滤波算法用S4方法进行参数选择。

本文以民用涡扇发动机为对象，在原有7个控制参数基础上增加5个候选监测参数。针对部件故障诊断需求，利用lsqnonlin非线性优化函数及遗传算法，依据统一的诊断标准在32种方案中选择最优的参数集，并在基于GasTurb/MATLAB的航空发动机部件级模型[9]上进行验证，结果表明该方法可以应用于国内民用涡扇发动机监测参数的选择。

1 建立涡扇发动机模型

基于文献[9]的方法建立涡扇发动机模型，其非线性模型定义为：

(1)

式中：x为状态向量；h为蜕化参数向量；u为输入向量；z为定义飞行条件的可测参数向量；ym为可测输出向量；yu为不可测输出向量。各向量适维。

在确定飞行条件下的基准性能稳定工作状态点(xss,uss,yss,href)处，对式(1)进行线性化，可得其状态变量模型为：

(2)

式中：Δx=x-xss；Δu=u-uss；Δy=y-yss；Δh=h-href；A，B，L，Cm，Dm，Mm，Cu，Du，Mu均为系统矩阵。

从式(2)可以看出，仅从数学意义上来说，Δh与Δu的作用相同，都可当成控制输入，因此将式(2)转化为如下标准形式：

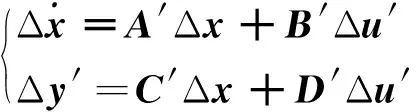
(3)

在设计点工作状态(高度H=11 km、马赫数Ma=0.8、低压转子转速NL=100%NL,design)下，得到高低压转子转速的状态变量模型。发动机非线性模型与所建立的状态变量模型响应曲线拟合情况如图1所示。图中，y1为低压转子转速，y2为高压转子转速，y1.(sim)表示低压转子转速的拟合情况，y2.(sim)表示高压转子转速的拟合情况。由图1可知，y1非线性模型与状态变量模型的拟合精度为99.79%，y2非线性模型与状态变量模型的拟合精度为99.94%，精度符合要求。

基于文献[10]的方法设计控制器，闭环控制后低压转子阶跃响应曲线如图2所示。由图2可得，发动机实际转速的最大值为4 603 r/min，超调量几乎为0，因此所设计的控制器符合要求。

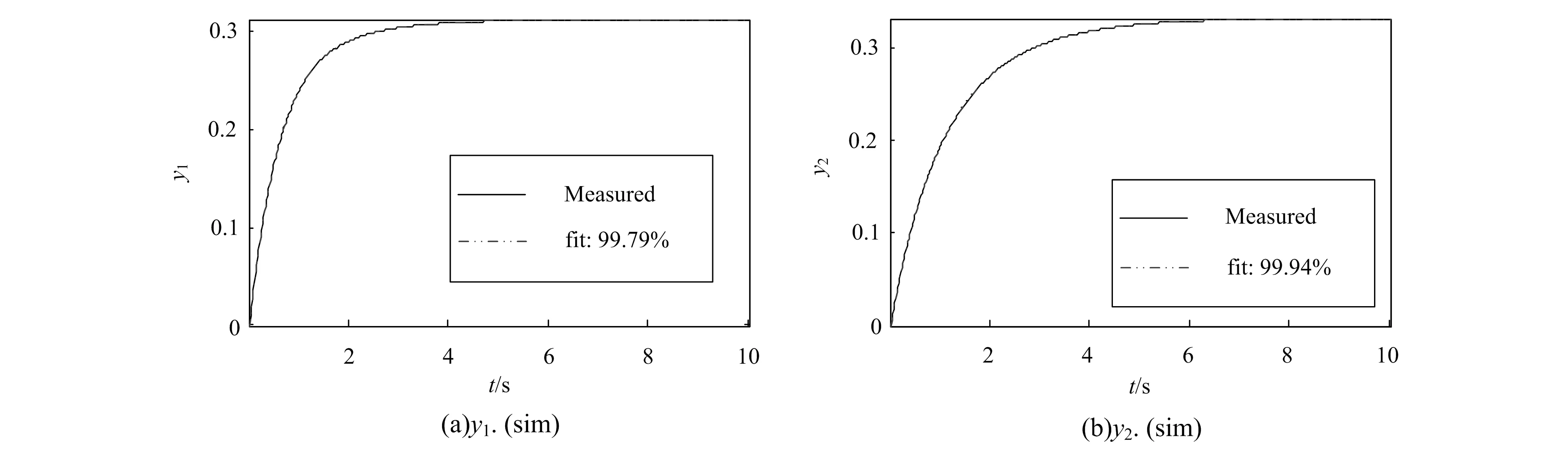
图1 燃油流量阶跃1%时响应曲线拟合情况

图2 闭环控制后的低压转子阶跃响应曲线

2 故障诊断及监测参数选择

故障诊断模型可以简化为测量参数与故障特征之间的代数关系，如果现实允许的话，也可以用试验数据或飞行数据建立模型。本文中，所用的模型为第1章中设计的有控制器的涡扇发动机部件级模型，该模型可在不同条件下，模拟出测量参数和健康参数的变化情况，为监测参数选择和验证提供数据支持。

表1为发动机控制及监测参数，其中噪声标准偏差是以标称状态下参数的稳态值为参考量的百分比[11]。部件故障包括风扇故障、高压压气机故障、高压涡轮故障和低压涡轮故障。

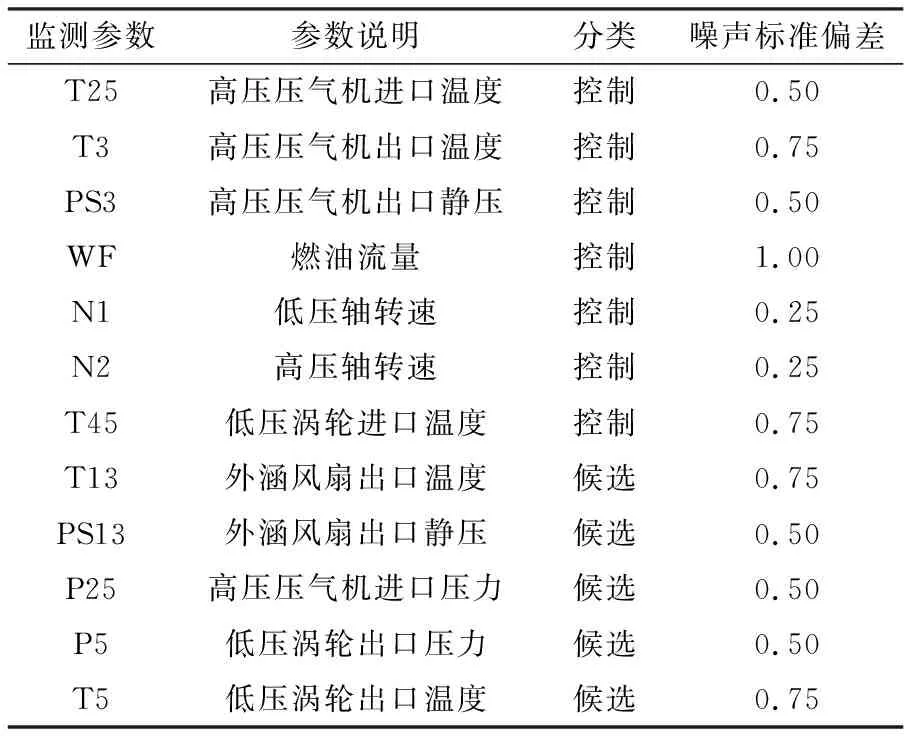
表1 控制及监测参数

2.1 建立故障模型

部件故障定义为其健康参数的衰退，即效率和流量的变化。对于每一类发动机部件故障，通过同时调整该部件的效率e和流量f等健康参数来模拟部件故障，此时部件的其他健康参数维持标称值。式(4)[12]用来确定每个发动机部件出现故障时，其效率和流量的调整量。

(4)

式中：f∶e为故障率；Fmag为故障幅值；eadj和fadj为部件健康参数调整值。

对于每一部件来说其f∶e均为定值，且最大故障幅值为0.07，见表2。从小到大均匀设置15个故障幅值插值点，由式(4)得到各部件健康参数调整值eadj和fadj，代入发动机模型进行计算，模拟部件级故障，并生成模拟的发动机测量数据。

表2 发动机部件故障

注：FAN表示风扇，HPC表示高压压气机，HPT表示高压涡轮，LPT表示低压涡轮。

2.2 测量数据处理

为了提高数值稳定性，测量数据先要经过处理，处理过程如下：

(5)

式中：yi为处理后的参数值；yfauli,i为出现故障时的参数值；yno min al,i为参数的标称值；σi为噪声的标准偏差。

2.3 生成故障数据

依据2.1和2.2步骤，生成不同部件的故障，表3列出了故障幅值为0.03时不同故障率下的数据。

2.4 基于lsqnonlin非线性优化函数的故障诊断与隔离

对于每一组候选参数集，先利用参数均方根值超限法来检测故障，检测出故障后，再隔离故障，并计算诊断性能值Dk，当故障不可检测时，Dk=0。参数集的均方根计算式为：

(6)

式中：RMSk为第k个候选参数集的均方根；mk为第k个候选参数集中的参数个数。

表3 处理后的故障数据(故障幅值0.03)

检测出故障后，建立基于lsqnonlin的非线性优化函数[13]来隔离故障并输出诊断性能值。

(7)

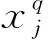
(8)

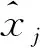
目标函数为：

(9)

2.5 诊断性能值计算

诊断性能值的计算公式[14]为：

(10)

式中：Dk为第k个参数集的诊断性能值；dj为故障j的诊断性能值；Cj为故障j的权重系数；Zj为故障j的诊断性能度量。可以根据故障的危急程度定义Cj的大小，本文中设置Cj为1，认为所有故障的危急程度一致。Zj的计算公式为：

(11)

式中：当估计故障与真实故障一致时，a为-1，不一致时，a为1；Rl为估计故障l的测量残差。Rl表示估计故障l恢复解的质量指标，在故障诊断评估的过程中，各故障通过恢复解处的测量残差进行恢复。测量残差作为故障恢复解的质量指标度量，见式(12)：

(12)

2.6 遗传算法选择过程

遗传算法实现过程如图3所示，通过遗传算法进行选择，最终选择出最优的诊断性能值Meritk，k

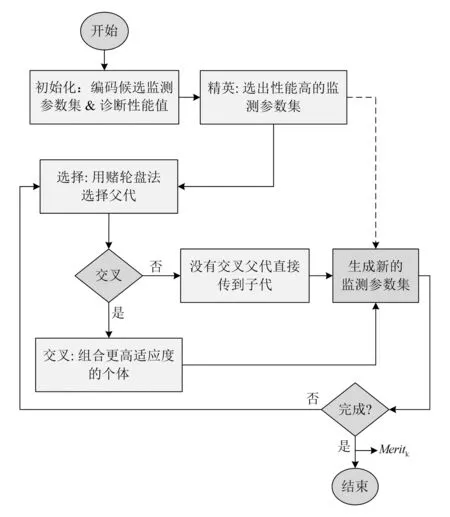
图3 遗传算法计算流程图

3 结果验证

选择过程中要计算所有候选监测参数集的诊断性能值，并根据性能值进行优劣排序，由于选择过程的计算量很大，因此为了减小计算量，要忽略一些次要因素。在此基础上，选择几组性能值较高的监测参数集，考虑次要因素的影响进行结果验证，由于此时候选监测参数集个数大大减小，因此可以进行各种因素的验证。

在实际的系统中，测量参数时总是混杂着测量噪声，因此本节要考虑的因素就是参数的测量噪声。

在验证过程中，给每个测量参数叠加了随机噪声从而产生了更大的样本集。具体实现方法是给每个测量参数叠加100次正态分布的随机噪声序列，将故障测试数据的向量扩展成多维增广传感器监测参数序列。图4展示了3个监测参数和5个噪声数据的叠加过程。

图4 增加随机噪声的监测参数

4 结果分析

4.1 故障检测结果

当故障幅值为0.005时，所有高压压气机故障均不可检测，风扇、高压涡轮和低压涡轮故障可检测；当故障幅值为0.01时，在前文所提的32种方案中，有15种参数集的高压压气机故障不可检测，而包含P25的另外17种参数集则可检测出所有部件故障；当故障幅值大于0.01时，所有故障在32种参数集中均可检测。

4.2 选择结果分析

表4是以增加一个P25监测参数为例，诊断模型的输出结果。

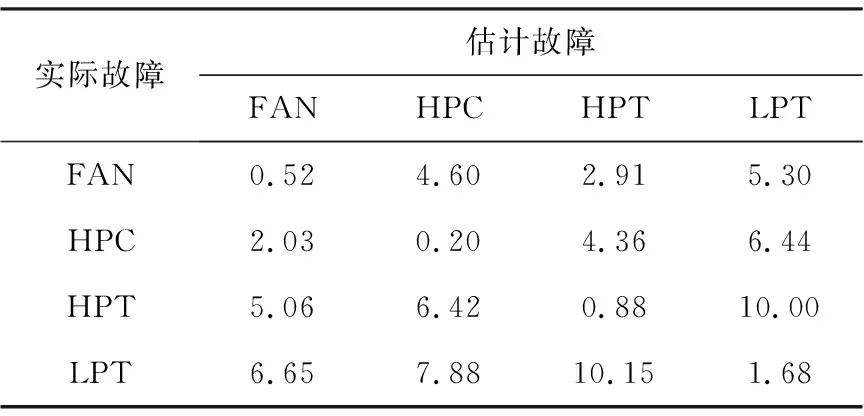
表4 诊断模型的输出(增加P25)

表4表明，对每一种实际故障，诊断模型估计出4类故障。表中对角线值最小，如在风扇故障估计中，对应的对角线值最小，所以估计的结果是准确的。

最后得到的结论是，当增加1个监测参数时，监测参数的选择方案优劣排序为P25 > T5 > PS13 > P5 > T13，即增加P25结果最优。

增加2个监测参数时，选择方案优劣排序为P25&T5>P25&PS13>P25&P5>P25&T13>T5& PS13>T5&P5>T5&T13>PS13&P5>PS13&T13>P5&T13，即增加P25和T5结果最优。表5列出了监测参数优化选择结果。表中Meritmax为候选监测参数个数一定时传感器诊断值的最大值，kadd为候选传感器的个数。

表5 监测参数优化选择结果

从表5可以看出，增加2个监测参数时，Meritmax达到最大，再增加监测参数的个数，Meritmax反而逐渐降低。原因是增加的参数没有明显的诊断优势，表现在两方面：一方面是因为均方根诊断本质上是测量残差的平均值，当增加的传感器y值较小时，整体的均方根值将会减小，因而故障更难诊断；另一方面是在故障隔离中，当传感器测量参数之间不独立时，模型的诊断性能降低，测量参数间的相互影响会降低优化过程的诊断效果。

4.3 结果验证

对增加随机噪声后每个部件的故障进行100次验证，生成xest(100×4×4)的故障估计数据，以及残差平方和数据resnorm(100×4×4)。第一维表示进行100次验证，第二维表示4种实际故障类型，第三维表示4种估计器类型。例如：xest(25,1,4)表示第25次验证中，风扇故障的低压涡轮估计器。另外，还生成了residual(100×4×4×n)四维残差数据，其中n随着监测参数集中参数个数的不同而变化，基准参数集的n为7，当增加P25参数时，最优监测参数集的n值为8，当增加P25和T5参数时，最优监测参数集的n值为9。对3种监测参数集各进行100次验证，求得3种监测参数集的诊断值均值Meritmax分别为58.31，68.49，70.99。在没有噪声的情况下，3种情况监测参数集的诊断值分别为58.42，68.51，71.17。由此验证了有噪声情况下所选监测参数的正确性。

5 结束语

本文基于lsqnonlin及遗传算法对涡扇发动机监测参数选择方法进行了研究，结果显示，针对发动机故障诊断,本文方法能够系统化定量地选择最优监测参数集，选择过程具有工程应用价值，可以用于民机健康管理中监测参数的选择。建立的故障诊断模型可以较好地隔离部件故障，在满足诊断精度的同时降低诊断成本。

该方法是系统方法，可以针对不同应用灵活扩展，用于不同系统、不同目的的监测参数选择。