公路隧道钢管混凝土拱架承载力评价指标及合理选型研究
张俊儒,王智勇,任兆丹,孔 超,徐向东,吴 洁
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;2.中铁第四勘察设计院集团有限公司,湖北 武汉 430063;3.西南科技大学土木工程与建筑学院,四川 绵阳 621010;4.中国电建昆明勘察设计研究院有限公司,云南 昆明 650051)
0 引言
随着我国交通建设规模的不断扩大,3车道、4车道的超大断面公路隧道频频出现[1]。在我国西南地区,由于宏观地质构造的影响,致使工程地质十分复杂,构造地应力高,板岩、千枚岩等软岩分布广泛。隧道在开挖过程中受高(极高)地应力的影响极易发生挤压性大变形,造成支护结构侵入隧道净空,不得不进行拆换处理,在造成材料浪费和工期延误的同时,也给隧道支护体系的设计与施工带来了极大的挑战。永宁(永安—宁化)高速公路的石林隧道[2]、兰渝铁路的木寨岭隧道[3-4]穿越复杂的断层带及破碎带,在隧道施工中出现工字钢拱架被压变形、喷射混凝土层出现开裂和剥落等病害,木寨岭隧道局部引起隧道侵限、塌方等灾害,最终通过加大初期支护刚度等措施解决了大变形段的问题。香丽(香格里拉—丽江)高速公路的海巴洛隧道[5]在施工中多次出现初期支护大变形等病害,通过现场实测发现上台阶开挖是引起围岩大变形的主要阶段,通过采用临时仰拱及双层支护等措施实现了变形控制。在成兰铁路的茂县隧道[6]通过现场试验发现,在挤压性软岩大变形隧道中,初期支护强度不足易导致大变形,最终采用钢架分层、分次施作的方式控制了变形。“刚性强支”的设计理念解决了云桂铁路新莲隧道[7]中高地应力、大变形的问题,充分调动围岩主动承载和刚性支护被动承载能力。由此可见,在高(极高)地应力、挤压性软岩大变形隧道的施工中,尽管地应力进行了适当的释放,但初期支护强度、刚度不足仍然是隧道发生破坏的重要影响因素。
1970年,钢管混凝土结构应用于日本青函海底隧道,采用圆钢管混凝土代替了一般的H型钢,防止了隧道的塌方,顺利通过了断层带[8]。钢管混凝土结构在我国隧道工程中的应用可追溯到衡广复线上的南岭双线隧道[8-9],发现钢管混凝土支护结构比其他类型钢支护结构减少钢材用量38%~54%,经济效益显著。京沪高速的龙鼎隧道[10]首次采用装配式钢管混凝土施工体系,有效控制了围岩变形,支护结构受力合理。Wang等[11]通过对高应力巷道的研究发现,钢管混凝土支护体系的承载力远大于U型钢拱架的承载力,钢管混凝土拱架发生急剧变形后,仍具有较高的后承载力。因此,钢管混凝土结构对于高(极高)地应力条件下软岩隧道大变形的控制具有极高的参考价值。
目前,钢管混凝土拱架在地下工程的研究中主要集中在巷道工程领域。其中,文献[12-13]采用1/4圆弧拱进行支架性能试验,发现钢管混凝土拱架具有良好的弹塑性性能、较大的承载力和变形性能。高延法等[14]首次提出了圆弧构件支护反力计算力学模型,并通过试验发现拱架的破坏方式为钢管屈服破坏,拱架的承载能力是相同质量U型钢拱架的2~3倍;Chang 等[15]采用ABAQUS对试验进行了相同条件下的数值计算,得到了较高的一致性;随后刘国磊[16]通过试验推导了钢管混凝土圆弧拱抗弯能力的计算公式;王军[17]在此基础上分析了荷载形式与矢跨比对圆弧拱承载性能的影响。刘珂铭等[18]采用钢管混凝土复合支护技术,有效地控制了大断面极软岩巷道的变形。李术才等[19]通过试验发现,钢管壁厚比核心混凝土强度对拱架极限承载力的影响更为显著。李为腾[20]推导了钢管混凝土圆弧拱抗弯能力的计算公式。Jiao等[21]发现当U型钢截面弯矩达到一定值后,开口截面会迅速张开,从而导致整体抗弯能力降低。针对此问题,李为腾等[22-23]提出了U型约束混凝土拱架支护方法,具备较好的延性和后期承载力。王琦等[24]通过研究发现,钢管混凝土支架与相同含钢量的U型钢支架、格栅钢架、空钢管支架相比,在满足承载力的同时可以降低成本。侯和涛等[25]以济南某电力隧道为例,发现薄壁钢管混凝土的抗变形能力要优于传统的格栅钢架。江贝[26]通过试验发现,随着核心混凝土强度的提高,钢管混凝土拱架的极限承载力逐渐增强,但承载力提高率明显降低;钢管混凝土拱架的极限承载力与钢管壁厚基本呈线性关系。谷拴成等[27]指出钢管与混凝土材料以及两者的几何特性与物理特性对钢管混凝土拱架的力学性能有着重要的影响,但只给出了部分钢管混凝土拱架设计型号,并没有进行系统的研究。
以上对于钢管混凝土拱架的研究大多以巷道工程为研究背景,本文所研究的交通隧道与巷道工程有所不同,具有断面更大、断面形状更复杂的特点;目前的试验研究已经初步掌握了钢管混凝土拱架的宏观承载特性,但对于钢管混凝土拱架承载力的评价方法没有具体的阐述,对于钢管混凝土拱架合理选型也没有具体的研究。基于以上背景,本文采用理论计算与数值模拟的方法,探究钢管的相关参数与钢管混凝土拱架承载力的关系,得出钢管混凝土拱架承载力的评价指标及合理选型方法,以期为今后钢管混凝土支护结构应用于隧道及地下工程领域提供理论依据。
1 钢管混凝土拱架承载力理论计算
钢管混凝土拱架承载力的理论计算,大多是以钢管混凝土短柱轴压承载力为计算依据,然后在此基础上引入折减系数进行修正,得到不同压弯工况下的承载力。本文以蔡绍怀[28]的钢管混凝土构件承载力计算理论为依据,再结合高延法等[14]的钢管混凝土拱架力学模型进行理论计算。
1.1 钢管混凝土构件及拱架承载力计算理论
蔡绍怀[28]通过一系列试验与研究提出了套箍指标θ(见式(1))以及轴心受压构件的承载力计算公式(见式(2)),用来计算钢管混凝土短柱的极限承载力;同时提出了钢管混凝土压弯构件的承载力计算公式(见式(3))。通过考虑构件长细比以及偏心率对压弯构件承载力的影响,在短柱轴压承载力的基础上进行折减。
(1)
(2)
式(1)—(2)中:θ为套箍指标;N0为钢管混凝土短柱极限承载力;As为钢管的面积;fs为钢管的屈服强度;Ac为核心混凝土的面积;fc为核心混凝土的抗压强度设计值。
Nu=φ1φeN0。
(3)
(4)
(5)
式(3)—(5)中:Nu为钢管混凝土压弯构件极限承载力;φe为考虑偏心率对承载力影响的折减系数;le为构件等效计算长度;D为钢管混凝土外直径;e0为纵向力的初始偏心距;rc为核心混凝土横截面的半径。
高延法等[14]首次提出钢管混凝土拱架承载力计算力学模型,钢管混凝土拱架计算公式见式(6)。
(6)
式中:S为钢管混凝土拱架间距;R为钢管混凝土拱架计算半径;α为钢管混凝土拱架积分角度;p为钢管混凝土拱架承载力。
1.2 钢管截面参数与钢管混凝土拱架承载力关系
现有的双线铁路隧道或公路隧道,隧道上半断面设计近似于单心圆。研究选用设计速度为120 km/h的3车道公路隧道上半拱部作为计算断面,假设拱架上半拱部承受均匀围岩压力[16],侧压力系数为1,钢管混凝土拱架力学模型如图1所示。将断面参数代入式(1)—(6),推导出钢管混凝土拱架承载力的表达式,并将钢管混凝土压弯承载力Nu用考虑了折减系数的钢管混凝土短柱轴压极限承载力N0表示,见式(7)。

图1 公路隧道钢管混凝土拱架力学模型
(7)
(8)
式中β为综合折减系数,β=φ1φe。
隧道的上半拱部为圆弧形,在围岩形变压力作用下每一弧段的受力形式基本一致。因此,可将式(7)中的φ1φe用综合折减系数β代替(0<β≤1)。则式(7)可以简化为式(8),即钢管混凝土拱架承载力p是钢管混凝土柱轴压承载力N0的一次函数。为进一步研究钢管截面参数与钢管混凝土拱架承载力的关系,取β=0.6[20],β的变化并不会影响钢管参数与钢管混凝土拱架承载力之间的关系。计算过程为:首先根据式(1)及式(2),由钢管与混凝土的参数计算出其轴压承载力N0;再通过式(8)计算出钢管混凝土拱架的承载力p。
为了分析钢管不同截面参数对钢管混凝土拱架承载力的影响,共对50种不同钢管直径、壁厚的钢管混凝土拱架进行计算。钢管均采用Q235钢材的参数进行计算,屈服强度fs为235 MPa;核心混凝土均采用C40混凝土的参数进行计算,抗压强度设计值fc为19.1 MPa[29]。
图2—5分别示出50种工况下钢管面积、含钢率、惯性矩、抗弯截面系数与钢管混凝土拱架承载力理论值p拱的关系曲线。

图2 钢管面积-钢管混凝土拱架承载力曲线
由图2和图3可知,在同一种钢管直径下,钢管混凝土拱架承载力与钢管面积、含钢率呈现一定的规律性,但不同钢管直径之间的规律相差较大,曲线离散性较大。由图4可知,钢管壁较薄时,钢管截面惯性矩能够较为一致地体现钢管与钢管混凝土拱架承载力之间的关系,但随着钢管壁厚的增大,曲线离散性逐渐变大。由图5可知,不同直径、壁厚的钢管混凝土拱架承载力与钢管抗弯截面系数的关系较为一致,规律性较为明显。故由图2—5可知,钢管的惯性矩、面积以及含钢率均不能表征在不同直径、壁厚下钢管与钢管混凝土拱架承载力的关系,只有钢管的抗弯截面系数能够较为一致地反映钢管与钢管混凝土拱架承载力的关系。因此,可以选取钢管抗弯截面系数作为钢管混凝土拱架承载力的评价指标。

图3 含钢率-钢管混凝土拱架承载力曲线

图4 钢管惯性矩-钢管混凝土拱架承载力曲线

图5 钢管抗弯截面系数-钢管混凝土拱架承载力曲线
图6利用二次多项式拟合了50种工况下的钢管抗弯截面系数与钢管混凝土拱架承载力数据,得到钢管抗弯截面系数与钢管混凝土拱架承载力之间的函数表达式(见式(9)),拟合度达到0.991。该公式适用于圆形钢管混凝土拱架承载力的计算,且核心混凝土为C40素混凝土,钢管为Q235钢材,侧压力系数取1。

图6 钢管抗弯截面系数-钢管混凝土拱架承载力拟合曲线
(9)
式中Wz为钢管抗弯截面系数,m3。
2 钢管混凝土初期支护承载力数值模拟
钢管混凝土初期支护是由钢管混凝土拱架与混凝土喷层组成,二者协调变形共同承载。针对理论计算的结果,本节将采用数值计算的方法验证理论计算的结果与规律是否适用于钢管混凝土初期支护,并分析产生差异的原因。
2.1 本构模型
为了更好地模拟钢管混凝土拱架在隧道中的受力机制,将2根钢管混凝土拱架嵌入喷射混凝土中,即采用“Embeded”约束[30],喷射混凝土通过约束钢管混凝土拱架节点的自由度实现两者的协调变形,从而实现对两者黏结作用的模拟;钢管采用Q235钢材,本构关系采用如图7所示的双线性模型,其数学表达式见式(10)[29, 31]。钢管弹塑性模型参数见表1。

表1 钢管弹塑性模型参数

图7 钢材本构关系
(10)
式中:σgc为钢材应力;Es为钢材的弹性模量;ε为钢材应变;εs为钢材最大弹性应变。
核心混凝土是钢管混凝土拱架承载体系的重要组成部分,而外部喷射混凝土能够提高钢管混凝土拱架的纵向稳定性,在计算中两者均不可忽略。因此,核心混凝土与喷射混凝土均采用混凝土塑性损伤参数(见表2[29]),喷射混凝土强度等级均为C25,核心混凝土强度等级为C40。该模型能够较好地表示混凝土在荷载作用下的塑性变化以及刚度退化,当在计算中混凝土达到混凝土塑性损伤模型中的峰值压应力时,混凝土将进入软化阶段,主要表现为材料的弹性模量不断下降,直至不能继续承载[28],其应力-应变关系[29-30]为:

表2 C25/C40混凝土塑性损伤模型参数
(11)

2.2 有限元网格划分及边界条件
核心混凝土与喷射混凝土建模均采用实体单元,当钢管壁厚为1 mm和2 mm时采用壳单元,其余壁厚下的钢管均采用实体单元。核心混凝土与喷射混凝土以及实体单元的钢管均采用减缩积分格式的六面体单元划分网格(C3D8R),壳单元的钢管采用减缩积分格式的四边形单元划分网格(S4R)。钢管与核心混凝土采用Tie约束[20],钢管混凝土拱架间距取1 m,喷射混凝土的厚度为0.28 m。
将钢管混凝土拱架及喷射混凝土的拱脚进行三向约束,荷载为加在喷射混凝土外表面上的面荷载,单位为MPa。钢管混凝土初期支护有限元模型如图8所示。

图8 钢管混凝土初期支护有限元模型
2.3 钢管截面参数与钢管混凝土初期支护承载力关系
根据数值计算结果,分别绘制了钢管面积、含钢率、惯性矩以及抗弯截面系数与钢管混凝土初期支护承载力p初曲线,如图9—12所示,各曲线与理论计算的曲线高度吻合。由图9—11可知,在同一钢管直径下,钢管面积、含钢率以及钢管的惯性矩与钢管混凝土初期支护承载力有一定的规律;但不同钢管直径之间,曲线离散性较大。由图12可知,在不同钢管直径、钢管壁厚下,钢管抗弯截面系数与钢管混凝土初期支护承载力的关系较为一致,能够较好地反映钢管与钢管混凝土初期支护承载力之间的关系,与上一节的理论计算结果相对应。

图9 钢管面积-钢管混凝土初期支护承载力曲线

图10 含钢率-钢管混凝土初期支护承载力曲线

图11 钢管惯性矩-钢管混凝土初期支护承载力曲线

图12 钢管抗弯截面系数-钢管混凝土初期支护承载力曲线
数值计算结果表明,在钢管的截面特征参数中,相比较于钢管面积、含钢率与惯性矩,钢管抗弯截面系数与钢管混凝土拱架承载力关系较为密切,曲线的离散性较小,更能表征不同直径、壁厚下钢管与钢管混凝土初期支护承载力的变化规律。综合分析解析计算及数值计算结果得到,因钢管抗弯截面系数能够较好地反映钢管与钢管混凝土拱架承载力之间的关系,建议采用钢管抗弯截面系数作为钢管混凝土初期支护承载力的评判指标。
通过对比钢管混凝土拱架承载力的理论值与钢管混凝土初期支护承载力的数值计算结果可知,理论计算结果小于数值计算结果。原因有以下几点:
1)考虑了喷射混凝土的作用。喷射混凝土自身具有一定的承载力,而且对钢管混凝土拱架具有一定的约束作用。
2)理论计算中钢管混凝土拱架承载力的综合折减系数考虑不充分,与钢管混凝土拱架的实际情况有所偏差。
3)数值计算中考虑了材料的塑性阶段,而在理论计算中只考虑了材料的弹性阶段。
因此,基于钢管混凝土拱架承载力的理论计算与数值计算结果,进一步拟合钢管混凝土初期支护承载力公式。钢管混凝土拱架承载力-钢管混凝土初期支护承载力曲线如图13所示。对50种工况下的钢管混凝土拱架承载力理论计算与数值模拟结果进行线性拟合,得到钢管混凝土拱架承载力与钢管混凝土初期支护承载力公式(见式(12))。该公式适用于圆形钢管混凝土初期支护承载力的计算,且核心混凝土为C40素混凝土,喷射混凝土为C25素混凝土,钢管为Q235钢材,侧压力系数取1。

图13 钢管混凝土拱架承载力-钢管混凝土初期支护承载力曲线
p′=1.74×10-3×p+0.429。
(12)
式中p′为钢管混凝土初期支护承载力,MPa。
3 钢管混凝土拱架合理选型研究
钢管混凝土的合理选型在钢管混凝土拱架的设计中尤为重要,合适的钢管混凝土不仅能够提供足够的支护强度,而且也可以获得较好的经济效益。李术才等[19]通过研究发现,钢管壁厚对于钢管混凝土拱架的影响比核心混凝土强度等级对钢管混凝土拱架的影响更大,即增大钢管壁厚比提高核心混凝土的强度等级能够更快地提高钢管混凝土拱架的承载力。因此,基于上节研究得到的结论,进一步探究钢管直径与钢管壁厚对钢管混凝土拱架承载力的影响。
由于钢管的抗弯截面系数能够较好地表征钢管与钢管混凝土拱架承载力的关系,通过研究钢管壁厚、直径随钢管抗弯截面系数变化的规律,从而推导出钢管壁厚、直径与钢管混凝土拱架承载力的关系,为钢管混凝土的合理选型提供理论依据。钢管的抗弯截面系数计算公式见式(13)。
式中:t为钢管壁厚;d为钢管内径。
对式(13)中的D、t分别求二阶偏导,可得:
(14)
(15)
由式(14)可知,钢管直径对于钢管抗弯截面系数的二阶偏导数大于0,说明钢管直径对于钢管抗弯截面系数的影响越来越大,对于钢管混凝土拱架承载力的影响也越来越大。由式(15)可知,钢管壁厚对于钢管抗弯截面系数的二阶偏导数小于0,说明钢管壁厚对于钢管抗弯截面系数的影响越来越小,对于钢管混凝土拱架承载力的影响也越来越小。由此可见,增大钢管直径比增加钢管壁厚能够更快地提高钢管混凝土拱架的承载力。同时考虑到用钢量因素,建议尽量选择直径较大、壁厚较小的钢管型号。所以建议按照以下优先级进行钢管混凝土选型:增大钢管直径>增加钢管壁厚>提高核心混凝土强度等级。
钢管直径-钢管壁厚-钢管抗弯截面系数散点图如图14所示。通过该散点图对比3种不同型号的钢管混凝土拱架,更加直观地说明钢管混凝土拱架合理选型的重要性。图14中3个蓝点分别为3种不同型号的钢管,以直径120 mm、壁厚12 mm的钢管1为基准,分别对比了直径140 mm、壁厚8 mm的钢管2,与直径160 mm、壁厚6 mm的钢管3,结果见表3—4。
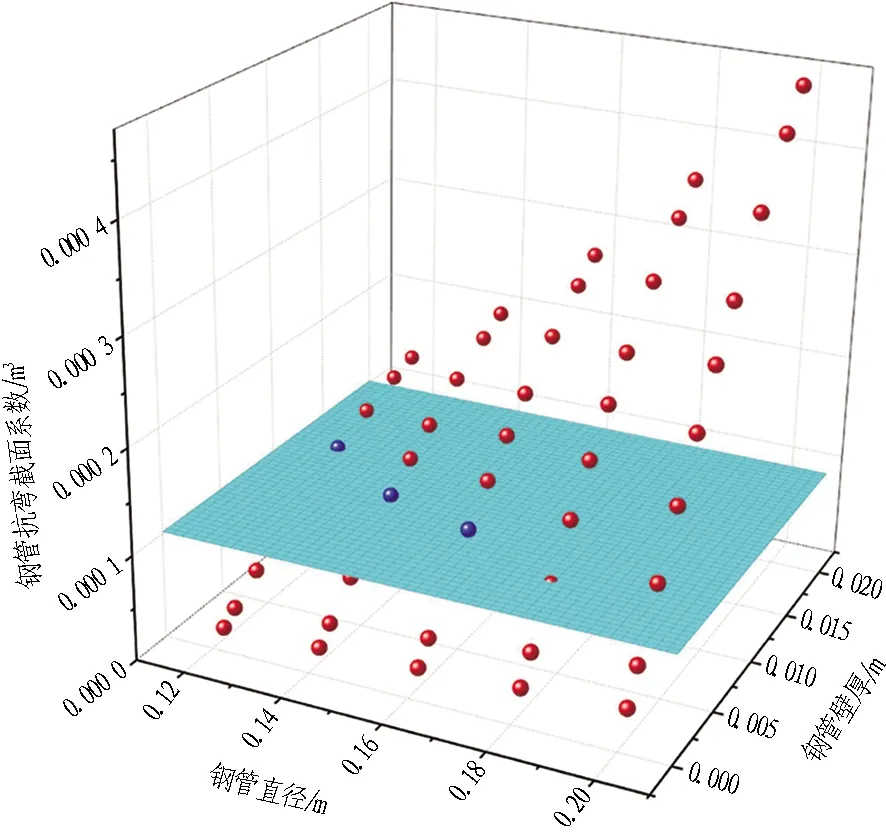
图14 钢管直径-钢管壁厚-钢管抗弯截面系数散点图

表3 钢管1与钢管2对比

表4 钢管1与钢管3对比
由表3—4可知,这3种类型的钢管抗弯截面系数相差不大,则其钢管混凝土拱架的承载力也相当,但通过对比钢管面积可知,直径160 mm、壁厚6 mm的钢管面积最小。由此可见,选择合适的钢管混凝土型号具有极高的经济价值,在同等承载力的条件下,建议选取直径大、壁厚小的钢管,钢管抗弯截面系数可以作为钢管选型的重要依据。
4 结论与讨论
1)运用理论计算方法研究了50种不同钢管直径、壁厚的钢管混凝土拱架承载力,相比较于钢管面积、含钢率以及惯性矩,发现钢管抗弯截面系数作为一个综合指标,能够表征钢管混凝土拱架的承载力,建议采用钢管抗弯截面系数作为钢管混凝土拱架承载力及初期支护承载力的评判指标。并拟合了钢管抗弯截面系数与钢管混凝土拱架承载力公式。
2)在钢管混凝土拱架的设计中,钢管抗弯截面系数可以作为钢管选型的重要依据。在同等承载力的条件下,建议按照以下优先级进行钢管选型:增大钢管直径>增加钢管壁厚>提高核心混凝土强度等级。
3)文中将钢管混凝土拱架上半部分假设为均匀受压,即假设侧压力系数为1。在后续的研究中,将进一步研究侧压力系数与钢管混凝土拱架承载力及钢管合理选型之间的关系。

