考虑质量衰退的批量调度与预防性维护的联合优化

陆志强，牟小涵

（同济大学机械与能源工程学院，上海201804）

传统的生产调度模型通常假设设备一直可用［1-2］，但在实际生产中，设备会随着使用逐渐老化。对此，常采用预防性维护来提高设备可靠度，降低因设备故障带来的生产损失。然而，过多或过少的维护，都会对生产效益产生不良影响。因此，考虑生产和维护的相互影响，联合优化二者，才有更高的实用价值。

近年来，生产调度和维护计划的集成问题逐渐成为制造领域研究的热点［3］。针对单机调度，Cassady 等［4］建立了单机调度与预防性维护的集成模型；蒋志高等［5］首次提出虚拟维护的概念，解决了加工时间可变的单机调度与维护问题；Cui等［6］研究了具有柔性预防性维护周期的单机调度问题。流水车间调度中，Allaoui 等［7］假设设备必须在周期T 内预防性维护一次；Miyata 等［8］提出维护级别的概念，并设计了有效的启发式算法；陆志强等［9］研究了流水线调度与维护集成模型的鲁棒性，并提出了三阶段启发式算法。

然而，上述文献都忽略了质量在生产调度与维护计划二者集成问题中的影响。为了提高经济效益，还要注意到因设备老化导致的产品质量劣化带来的损失。Hadidi等［10］对生产计划、调度、维护和质量的相关性模型和集成模型进行了综述；Pandey等［11］针对单机系统，开发了一个联合优化生产计划、维护策略和质量控制的模型；Jamshidi 等［12］提出了一个混合整数非线性模型来优化质量、维护、提前/延误和中断的成本。质量和设备的影响是相互的，工件质量的退化也会影响设备的退化状态，例如汽车装配线上由于来料质量缺陷引起的定位工具的故障［13］。这两者的耦合关系，使得设备间产生随机依赖性。随机依赖性多见于生产计划、维护与质量控制的集成研究中［14-16］，在生产调度、维护和质量三者之间的集成研究中则十分罕见。

综上所述，生产调度、维护与质量的集成研究较少，已有的集成文献也很少考虑随机依赖性。因此，本文针对串行流水线系统，考虑以质量衰退工件为媒介的设备间的随机依赖性，同时结合现代多品种和中小批量的生产特点，引入批量流概念，分批生产和传输［17］，建立生产调度和预防性维护的联合优化模型。

1 问题描述及数学建模

1.1 问题描述与假设

考虑一个串行流水线系统，在其调度期内，共有n个加工批次，需按照相同的工艺路线依次通过m台设备进行加工。每个加工批次可等量分成若干个子批次，每个子批次在一台设备上加工完成即可作为独立的转移批量转移到下一台设备，使得同一加工批次的前后工序交叉进行，减少设备的空闲时间，加快工件在设备间的流动。每台设备加工完一个子批次后进行一次设备检测，同时所有产品在系统末端进行质量检测，合格品用于满足需求，不合格品则需要返工。随着生产运行，各设备会随着使用逐渐发生退化，相应的加工工件的质量也会随之下降，设备间存在随机依赖性。为保证系统的有效输出，需要制定合适的维护策略。为了更清晰地描述研究问题，给出如下假设：

（1）在任一时刻，一台设备只可加工一个子批次，且一个子批次也仅能在一台设备上进行加工，不同加工批次的子批次不可交叉生产。

（2）考虑划分子批次产生的能耗成本，各加工批次划分的最大子批次数为2。

（3）所有工件均在零时刻到达，且设备在零时刻均可用。

（4）设备分为受控和失控两个状态。当设备处于受控状态时，其生产的产品均合格，当设备的退化状态超过给定的失效阈值时，设备将失控，产生质量失效，开始以恒定的百分比产生不合格品。

（5）只有通过检测才能发现设备的退化状态，检测时间忽略不计。若设备状态超过其给定的失效阈值，则进行大修，使得设备修复如新。否则，以预防性维护阈值为决策方式，超过它则进行预防性维护，设备修复非新，不考虑设备的随机失效。

（6）质量检测仅在系统末端进行，对不合格品只考虑返工成本，不占用所研究系统的生产能力。

1.2 符号定义

模型中用到的参数及相应定义如表1所示。

1.3 问题建模

（1） 维护策略模型

使用Gamma 过程来对设备的退化状态进行建模。令Dk(t)表示设备Mk在役龄t时的退化状态，则设备退化状态Dk(t)在一段时间ι 内的非负增量ΔDk(t)服从Gamma 分布Ga( x|αk( t )，βk)，其概率密度函数为

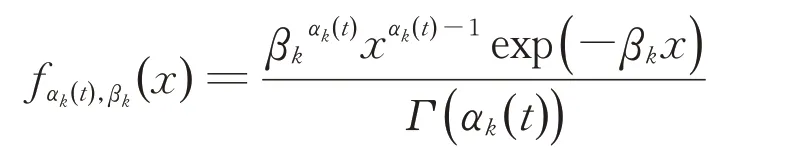
设备每加工完一个子批次后进行状态检测并实施相应的维护。若设备处于失控状态，则刚加工的子批次需在系统末端进行质量筛查。若设备处于受控状态，则对应的子批次无需进行检测。但为了防止在下一个子批次加工期间出现质量失效，采用预测维护策略，将下一批次加工期间的预测失效概率作为预防性维护阈值。考虑到每台设备设立不同的维护阈值会使得求解难度随着系统内设备数的增加而上升，因而假设所有设备都采用相同的预防性维护阈值Lpm。则在加工第o 个子批次中的预测失效概率可以表示为

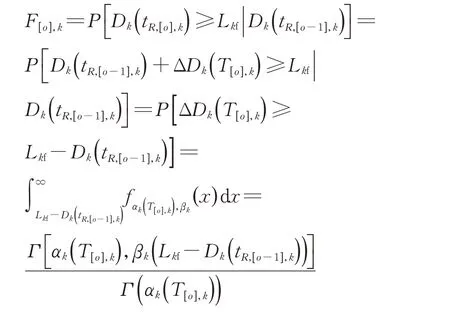
若F[o]，k≥Lpm，则设备Mk需在生产第o 个子批次前执行预防性维护。维护后，设备Mk的退化状态Dk有所改善，修复后设备的退化状态D'k遵循区间[0，Dk]的Beta分布，其概率密度函数为

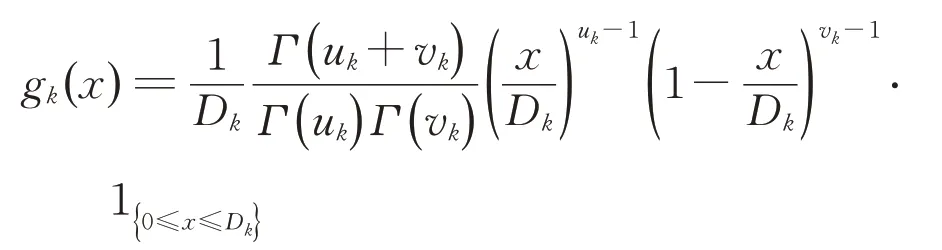
式中：uk和vk可通过极大似然估计从历史数据中获取；1{⋅}是示性函数；A 为真时1{A}=1，A为 假时1{A}=0。

表1 模型参数及其定义Tab.1 The definition of model parameters

来料质量和设备退化的相互关系导致设备间的随机依赖性，使用加速因子so，k'，k(so，k'，k≥0)来描述第o个子批次从上游设备Mk'输出对下游设备Mk退化的影响，若so，k'，k=0，则表示设备Mk'和Mk之间互不影响；否则设备Mk'的失控将加速设备Mk退化。使用Gamma 过程的形状函数来对该种随机依赖性建模，则有

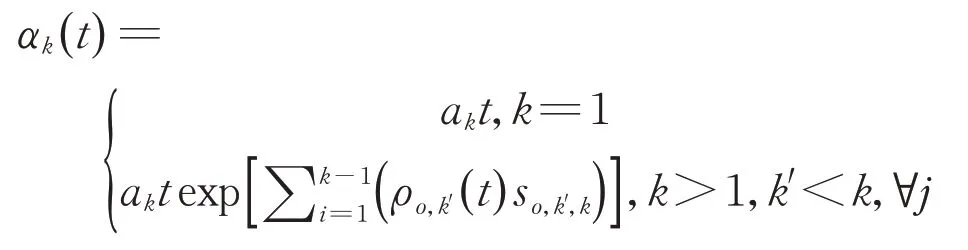
式中：akt是基准形状函数；回归函数ρo，k'(t)为上游设备是否失控的判断变量，其表达式可以写成

（2） 批量流调度与维护决策的集成模型

约束（1）～（2）表示加工批次和加工位置的一一对应关系。约束（3）确定各设备按加工顺序的单位加工时间。约束（4）～（5）确定了按加工顺序的子批次数量及加工批次的大小。约束（6）～（13）为子批次加工时间的约束，当需要维护时通过右移策略进行重调度，求得实际加工时间Sw，[o]，k。约束（14）～（15）为变量的取值约束。

（3） 目标函数计算

同时优化时间和成本两个目标。时间相关的优化目标为最小化完工时间的期望值，即f1=Ew(Cmax)。Cmax为最后一个产品的实际结束时间。

成本相关的优化目标为最小化能耗成本、维护成本及质量成本的期望值之和。划分子批次会产生设备准备能耗和传输能耗，能耗成本EC计算为

式中：ω1+ω2=1。f∗1和f∗2为单一目标最优值，即分别求解最小完工时间的期望值及最小相关成本值。

2 算法设计

本模型的求解是NP难问题，对此，设计了改进的差分进化算法。采用实值编码，n表示加工批次数，编码长度为(n+1)，前n个编码用于确定加工批次的顺序及是否划分批量，取值范围为(0，2)。整数部分用来确定是否划分批次；小数部分按升序排列加工批次的顺序。第(n+1)个编码表示维护阈值的大小，取值范围为(0，1)。给出一个实例来详细说明解码过程，如图1所示。

接下来对算法求解步骤进行详细描述：

（1）种群X(t)={XI(t)|I=1，2，...，Imax}初始化，Imax为种群中的个体数量，计算种群的适应度值，找到最优值对应的个体X∗(t)，适应度值f(X(t))通过蒙特卡洛仿真方法计算得到。

（2）变异操作

为了提高求解精度与加快收敛速度，利用鲸鱼算法［18］的搜索机制来进行变异。同时，考虑到标准鲸鱼算法存在容易陷入局部最优、收敛精度低的问题，引入了柯西变异算子［19］和非线性变化收敛因子［20］。

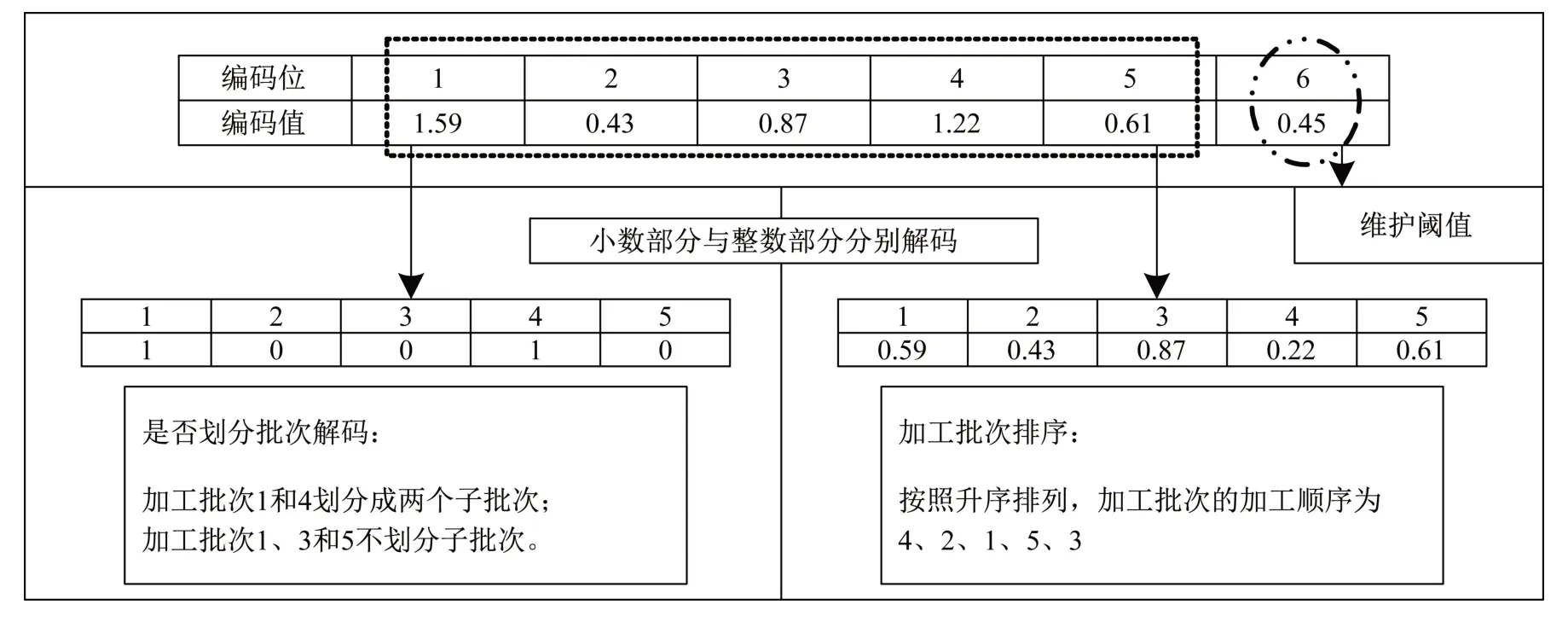
图1 解码过程示意图Fig.1 Schematic diagram of the decoding process

式中：N为收敛因子基准常量；t为当前迭代次数；tmax为最大迭代次数；μ∈(1tmax，1)为非线性调整系数。

（3）交叉操作

变异操作结束后，采用二项式交叉，表达式如下：

式中：XMu，I(t+1)交叉后的个体；CR是交叉概率；Mu(t+1)={XMu，I(t+1)|I=1，2，...，Imax}为 交 叉后的种群。

（4）变异和交叉结束后，通过选择决定子代个体是否进入下一代。

（5）设置迭代上限作为算法终止条件，输出求解结果，否则返回步骤（2）。算法流程如图2所示。

3 算例分析

3.1 改进的差分进化算法与标准进化算法比较

考虑m={3，5，8}，n={10，30，50}共9 种问题规模，表2给出了设备退化过程相关的参数，该生产系统的成本参数和时间参数如表3 所示，假设加工时间pj，k服从[1，3]的均匀分布，加工批次大小qj服从[20，100]的均匀分布，权重因子ω1=ω2=0.5。

由于目标函数由系统多次仿真的期望值表示，因此需要确定仿真的抽样样本数。通过选取4个具有不同决策变量的测试实例通过大量仿真来确定合理的样本数量。根据最终的实验结果，仿真样本量确定为50。

表2 各设备的退化与维护参数Tab.2 Parameters of different machines

图2 改进的差分算法流程Fig.2 The improved differential evolution algorithm flow

表3 其他成本和时间参数Tab.3 Cost and time parameters in production

在改进的差分进化算法（IDE）中，将种群大小设置为30，将最大迭代次数设置为50，并将交叉因子CR设置为0.4，标准差分进化算法（DE）变异因子设置为0.5，其余参数与IDE 相同。确定所有参数后，对算例进行求解，绘制各规模算例下的IDE迭代曲线，如图3所示，IDE与DE的求解结果对比如图4所示。从图3 可以看出，IDE 算法具有收敛性，对中小规模的算例求解效果较好，而且由于仿真计算时间的限制，该算法也不适用于更大规模问题的求解。从图4 可以看出，IDE 相较于DE 的求解结果较优，在设备数较少和规模小时求解效果更好。

图3 改进的差分进化算法的迭代曲线Fig.3 Iterative curve of improved differential evolution algorithm

3.2 与其他维护模型比较

记上文已建立的模型为P0；不考虑预防性维护仅考虑大修的维护模型记为P1；每次检查后都进行一次预防性维护或者大修的维护模型记为P2 以及忽略设备间的随机依赖性，单独求解每台设备的最优维护阈值的维护模型记为P3，将这几种维护模型进行比较，其对比结果如表4所示。

由表4 可以看出模型P0 的求解结果是最优的。通过对比发现，随着设备的增多，P0 的大修成本占总成本的比例增加，这是因为设备越多，设备间的随机依赖关系可能使得下游设备的退化加速，造成设备失效的同时产生不合格品，返工成本的占比增加也侧面印证了这一点。P1 的总维护成本高于P0 的总维护成本，说明安排预防性维护能够降低维护成本；此外，P1的返工成本远大于P0的返工成本，这是由于设备失效次数增多导致不合格品数量增加。P2的总维护成本总是高于P0 的总维护成本表明过度维护也会增加维护成本。P3的求解结果仅次于P0，说明忽视设备间的随机依赖性也会使得求解效果不佳。

图4 改进的差分进化算法与标准差分进化算法的求解结果Fig.4 The results of the improved differential evolution algorithm and the differential evolution algorithm

3.3 与其他生产模型比较

将不进行划分批次的模型记为P4；将单独决策模型，即先确定生产顺序及批次划分，再制定维护策略的模型记为P5，把二者的求解结果与P0的求解结果进行对比，如表5所示。

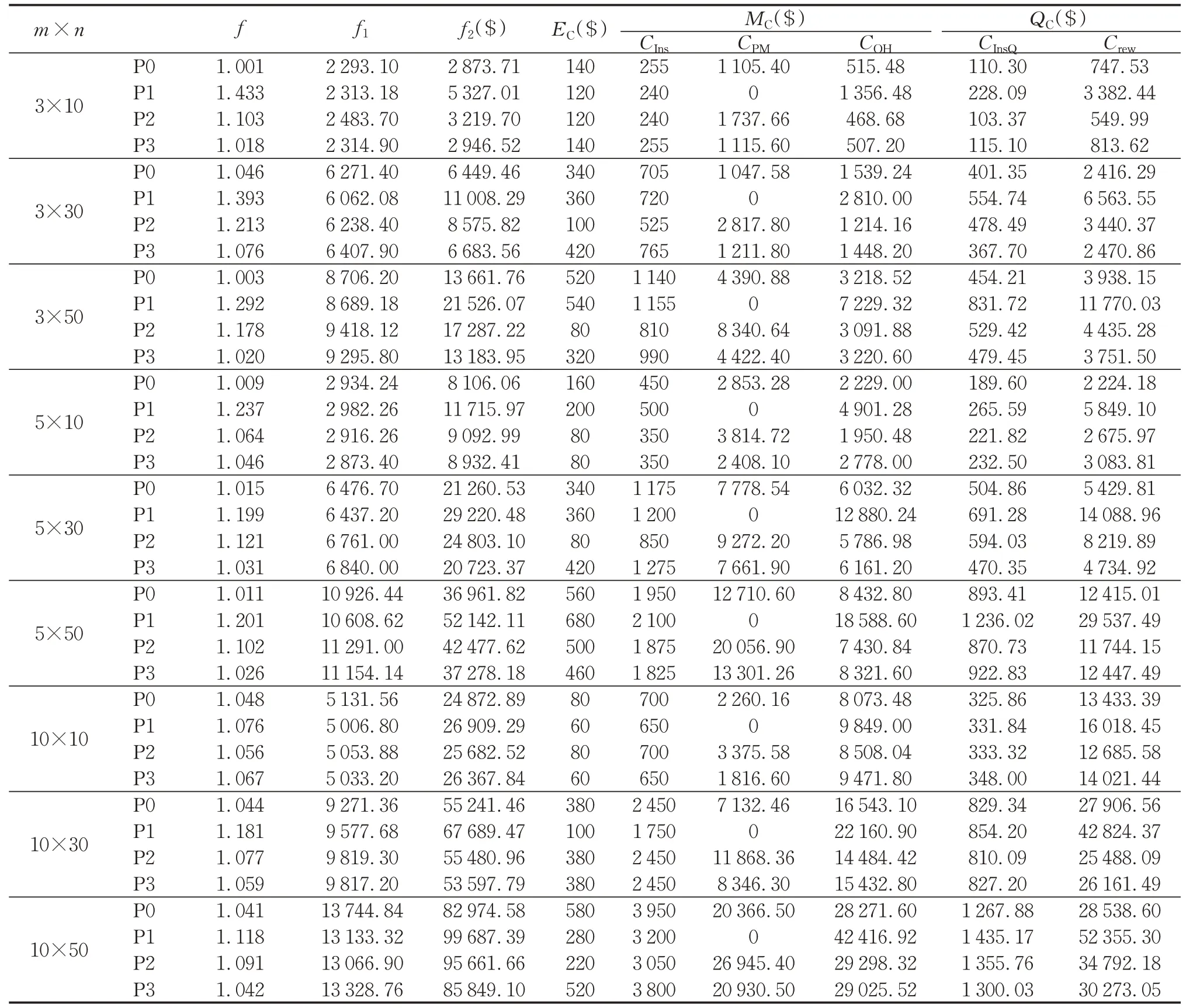
表4 不同维护模型下的结果Tab.4 The results obtained under different maintenance models

由表5可以发现，P5的求解结果次优于P0的求解结果，表明了集成模型较单独决策模型的优越性。P4的质量成本远大于P0的质量成本，原因是不划分批次的情况下，由于批次加工无法中断，且批次较大，设备在加工中失效的次数增多，相应的不合格品的数量也随之增加。选取一个5×10的算例分析批次划分次数对模型求解结果的影响，如图5所示，可以看出，随着批次划分次数的增多，期望完工时间不规律变化，此外，维护成本呈增加的趋势、质量成本呈下降趋势，但总成本是趋于减小的，说明适量选择划分批次次数才能同时优化总成本和期望完工时间。

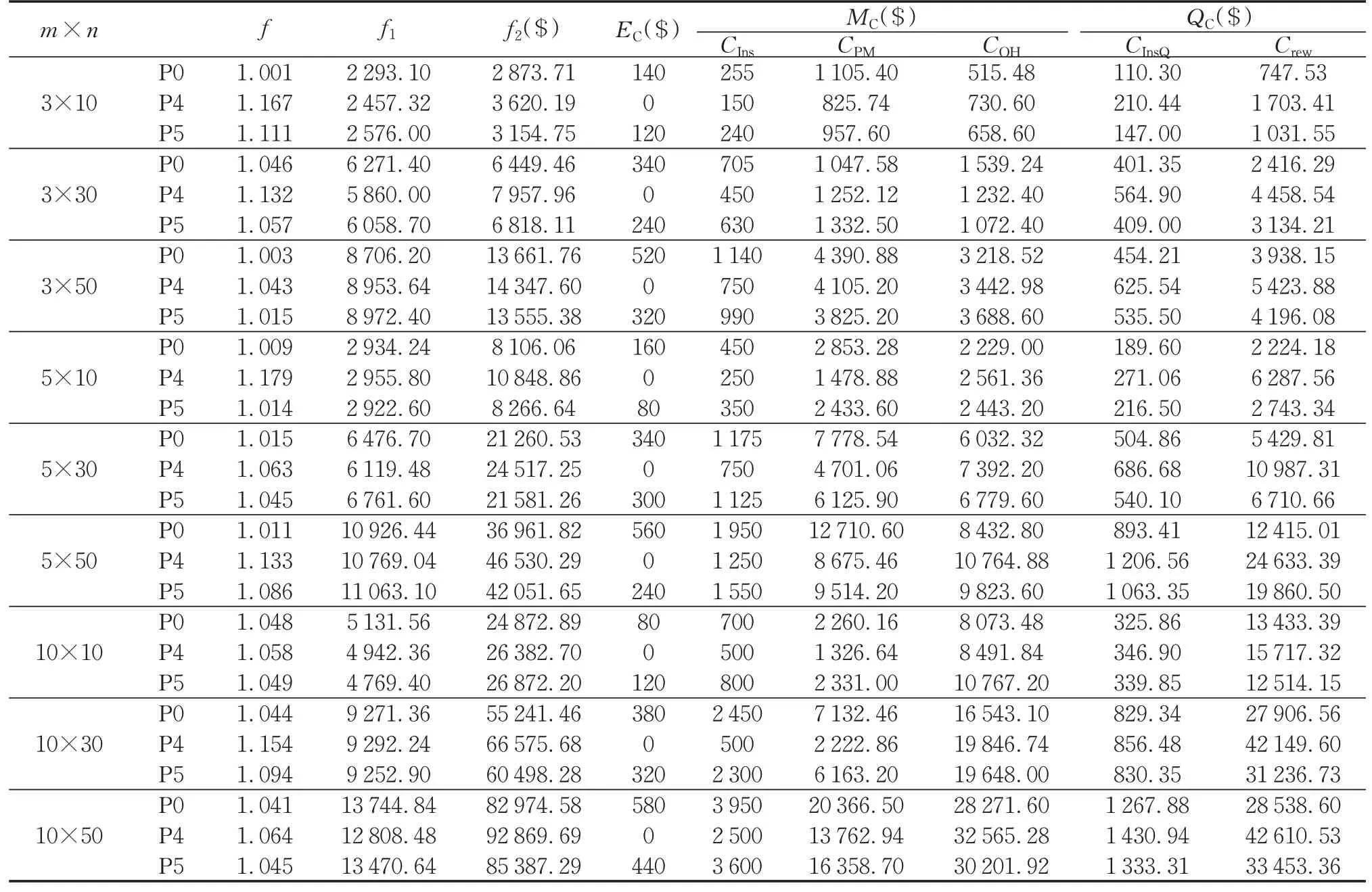
表5 不同生产模型下的结果Tab.5 The results obtained under different production models

图5 批次划分次数对求解结果的影响Fig.5 Influence of splitting times on the result

4 结语

本文考虑产品质量与设备退化状态之间的相互影响，以最小化完工时间和成本为目标，建立了考虑设备间随机依赖性的生产调度与维护的集成模型。此外，还引入了批量流的概念，通过算例分析得知适量划分批次可以优化总成本和期望完工时间。设计改进的差分进化算法对模型进行求解，数值实验的结果表明，该模型可有效规划生产排程、进行维护决策；并通过对比试验显示了该集成模型较单独决策模型的优越性。

本文以“批次在设备上加工完成”这一事件来触发设备的检测，存在检测后不进行维护的情况，即设备检测较为频繁，未来研究可以考虑对检测计划进行研究，以节省检测成本。此外，还可以考虑每台设备的加工顺序不同的状况，不等量分批的情形，以及引入机会维护的可能。