单指标分位回归模型估计的MM算法*
郭媛媛,杨雪梅,孙志华,3†
(1 中国科学院大学数学科学学院, 北京 100049; 2 华北电力大学数理学院, 北京 102206;3 中国科学院大数据挖掘与知识管理重点实验室, 北京 100190)(2019年5月14日收稿; 2019年10月9日收修改稿)
分位回归模型具有稳健的特点,并且能够对响应变量的分布做出精细的描述, 因此获得很多学者的关注。 目前, 分位回归方法已经成为分析数据的一个非常重要的工具,广泛地应用在金融、医疗、生物研究等领域。 分位回归模型的研究和应用可参考文献[1-4]及相关文献。 参数分位回归模型是在实际中应用广泛的一类回归模型[5]。但很多时候无法对参数分位回归模型进行正确的设定。基于误定的参数分位回归的统计推断结果经常是不可信的, 文献[6-7] 阐述了参数分位回归需要进行检验的必要性。非参数分位回归不存在误定的风险,但当样本量比较小且协变量比较多时,非参数分位回归方法可能会受到维数祸根的问题的困扰。
对分位回归,构建目标函数时用到的损失函数ρτ(r)=τr-I{r<0}具有不光滑的特点, 从而使得求解目标函数的最小值比较困难,且可能出现多个最小值点的情况,参见文献[5,8-11]。一种解决上面问题的方法是将分位回归模型的求解问题转化为线性规划问题,再利用单纯形法或内点法进行计算。不管是单纯形法,还是内点法,运算效率都不能令人满意。2000 年,Hunte和Lange[12]提出一种新的用于求解分位回归问题的算法,即MM算法。MM算法概念简单,易于执行,且数值稳定,比内点法拥有更强的数值计算能力。文献[11]对4种求解分位回归问题的算法,即内点法、MM算法、坐标下降法和ADMM算法进行比较研究,验证了MM 算法具有数值稳定和计算效率高的特点。
单指标分位回归模型具有降维的效果,同时保持了非参数分位回归的稳健性,其估计问题的研究吸引了很多研究者的兴趣。文献[13-14] 提出基于两步迭代的估计方法,文献[15-16]进一步提出不需要迭代的估计方法,文献[17-18]又提出基于贝叶斯方法的估计方法,文献[19-21]探讨单指标分位回归模型的变量选择以及加权复合单指标分位回归模型的估计。然而这些文献所提的估计方法都基于内点法来实现,内点法在计算分位回归模型时,计算效率低、耗时久,尤其在样本量较大的情况下,这种缺点更为明显。MM 算法在求解分位回归模型的估计时比较高效和便捷,这在文献[22-24]中均有体现,但是没有文献研究单指标分位回归模型的MM算法,故本文研究单指标分位回归模型估计的MM算法。
我们借鉴文献[12] 的方法,对单指标分位回归模型的每一步迭代程序中目标函数构建其替代函数,从而将复杂的优化问题简单化。然后,基于优化函数再进行求解计算得到估计值。我们构建的优化函数是光滑的,并能够保证每次迭代目标函数是下降的。数值模拟和实例分析结果表明基于MM 算法的估计程序具有较好的稳定性,能够得到比较准确的估计结果,并且相较于传统的内点算法具有更强的数值计算能力,用时更短。
1 单指标分位回归模型的估计介绍
对于给定的分位数τ∈(0,1),在给定x的条件下,响应变量y的τ分位数θτ(x)与协变量x之间的关系如下:
θτ(x)=g(xTγ),
其中x∈d是d维协变量,g(·)表示未知的一元联系函数。另外γ=(γ1,…,γd)T为未知的单指标向量,满足‖γ‖=1且γ1>0,‖·‖表示Euclidean范数。这个约束条件是为了模型的可识别性[25],已广泛应用在有关单指标模型的文献中。
本文采用局部线性方法对γ和g(·)进行估计,详细内容可参考文献[13],具体算法如下:
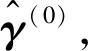
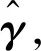
(1)
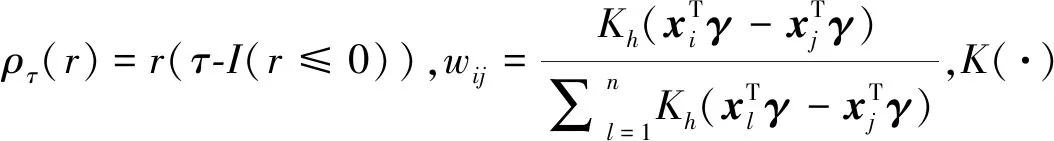
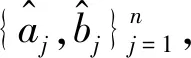
(2)
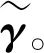
step 4重复step 1和step 2直至收敛。
(3)
2 估计程序的MM算法
2.1 MM算法介绍
下面介绍MM算法的基本思想。假设需要最小化的目标函数为L(θ):p→,θk为第k步的迭代值。MM算法每次迭代分两步来进行。首先,构造目标函数的优化函数Q(θ|θk):p×p→ 满足
Q(θk|θk)=L(θk),
Q(θ|θk)≥L(θ)∀θ.
(4)
然后, 对优化函数Q(θ|θk)进行最小化, 得到下一步的迭代值θk+1,则有
Q(θk+1|θk)≤Q(θk|θk).
(5)
综合式(4)和式(5),可知L(θk+1)≤L(θk)。这种下降趋势保证了MM算法具有显著的数值稳定性。
观察目标函数式(1)~式(3),可以发现它们均为非光滑函数, 因而不易得到最优解,故借用文献[12] 提出的MM 算法的思想来处理这个问题。其主要的处理方式如下:首先给ρτ(r)加一扰动ε,得到其近似函数
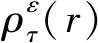
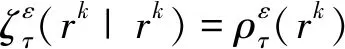
2.2 非参数部分的估计
首先,将式(1)中的目标函数修正为
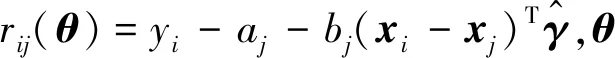
(6)
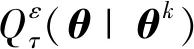
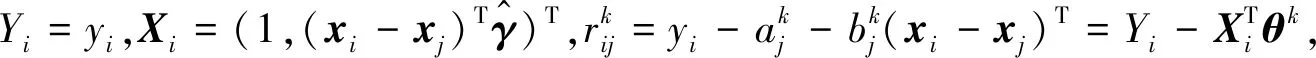
(7)
由此,可以将MM算法总结为如下步骤:
1) 选择迭代初始值θ0和一个较小的正常数ε,置k=0;
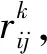
3) 令k=k+1,判断是否满足收敛准则,若满足收敛准则,即: 当
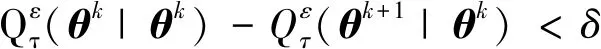
时,可终止迭代,其中δ是预先取定的足够小的数。否则返回2)继续迭代,直到满足收敛准则。
2.3 单指标向量的估计
首先定义式(2)中目标函数的近似函数:
在γk处的优化函数可以构建为
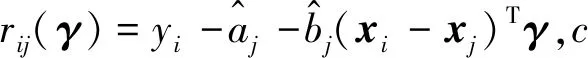
(8)
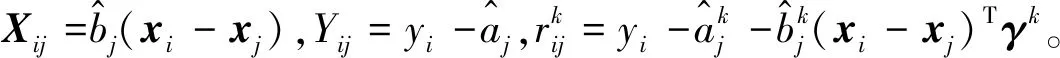
最后,可将基于MM算法的单指标模型的估计总结为如下步骤:
1)参考第1节step 1所提供的方法,得到γ的初始估计;
4)重复2)、3)步骤,直至收敛。
2.4 联系函数g(·)的估计
对于联系函数的估计,式(6)中目标函数式的近似函数可定义为
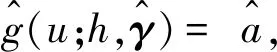
3 数值模拟
3.1 模拟1
借鉴文献[13]模拟1的模型设置,考虑模型
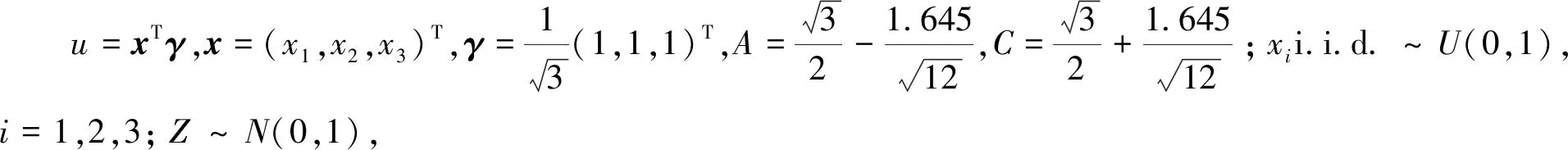
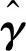
在不同的分位数下,计算上述评价指标值,所得结果列于表1和表2,可以看出,用MM算法计算单指标分位回归模型,无论是单指标向量的估计还是联系函数的估计,都有比较好的结果,且在较小和较大的分位数下依然有良好的表现,这表明本文所提出的计算方法是有效的。将该估计结果与文献[13] 中关于该模型的模拟结果进行对比,可以看出,用MM 算法计算单指标分位回归模型,与内点法相比,估计的精度是相似的,估计系数的偏差大小都在10-3~10-2,估计系数的样本标准差数量级均为10-2,但在计算效率上,本文所提出的方法大大优于内点法,这将在模拟3 中展示和说明。
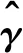
表1 模拟1中不同的τ下,估计的Bias、SE、MSE、CI、CPTable 1 The Bias、SE、MSE、CI、CP of under different choices of τ in simulation 1
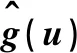
表2 模拟1中不同τ的选择下,的ASE、AAE的Mean、SETable 2 Outcomes of for the models under different choices of τ in simulation 1
3.2 模拟2
借鉴文献[13]模拟2的模型设置,考虑模型
驱动层介于系统层和硬件设备之间,提供应用程序访问硬件设备资源的接口,同时也为存储软件提供了基础环境和接口。linux系统将设备分为3类:字符设备、块设备、网络设备。考虑到安全存储的硬件加解密设备与块设备、网络设备特性的差异,而与面向流的字符设备类似,驱动层在采用字符设备的基础上提供相应的库文件供应用程序实现加解密功能[15]。
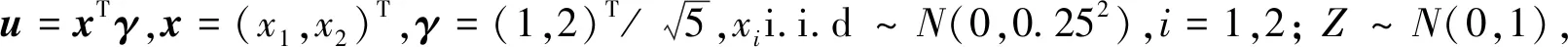
3.3 与内点法比较
由前两个模拟可以发现,MM算法在单指标分位回归估计的计算问题中表现良好,接下来比较MM算法与内点法的计算效率,考虑如下3个模型:
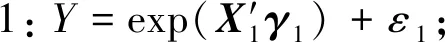
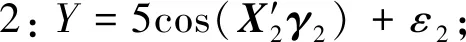
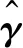
表3 模拟2中不同的τ下,估计的Bias、SE、MSE、CI、CP Table 3 The Bias、SE、MSE、CI、CP of under different choices of τ in simulation 2
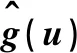
表4 模拟2中不同τ的选择下,的ASE、AAE的Mean、SE Table 4 Outcomes of for the models under different choices of τ in simulation 2
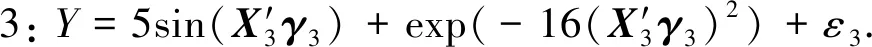
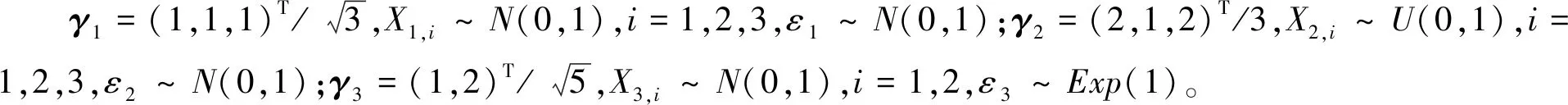
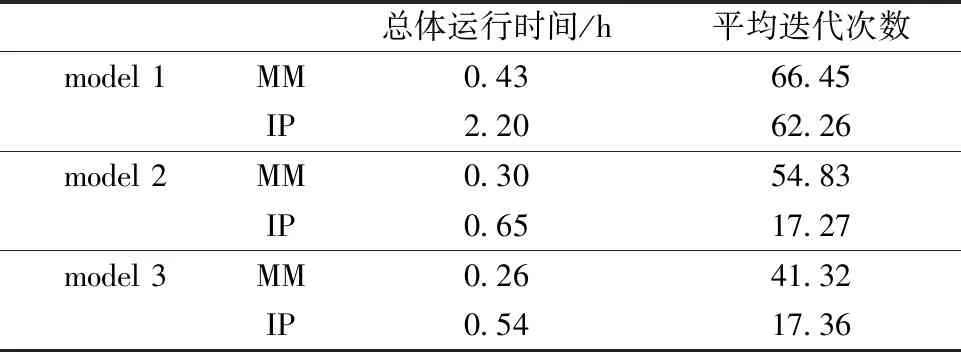
表5 n=100, 模型1、2、3的估计结果比较 Table 5 Estimation comparison among models 1, 2, and 3 with n=100
可以发现MM算法所用的时间远远少于内点法,且随着样本量的增大,这种计算效率上的优势更加明显。这是由于用内点法解决分位回归问题,是将目标函数及约束条件转化为线性规划问题,再用内点法来求解该问题,但转化之后的线性规划问题,协变量维数与样本量的大小有着正相关的关系,这种方法极大地增加了算法的计算量与所用时间。本文第3.2节 中的问题转化为线性规划后,协变量的维数为2n+p,第3.3 节 中的问题转化为线性规划后,维数为2n2+p,具体转化方法及维数的增加量可见文献[11]。而MM 算法只需对p维矩阵做运算,故两种方法的计算效率随样本量的增加会产生越来越大的差距。
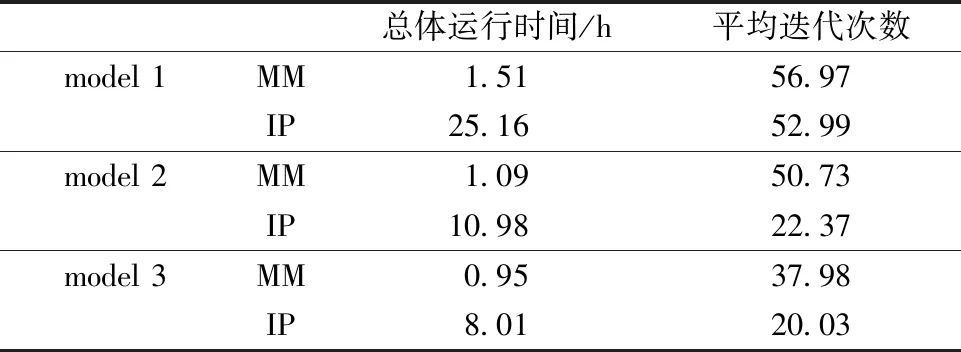
表6 n=200,模型1、2、3的估计结果比较Table 6 Estimation comparison among models 1, 2, and 3 with n=200
4 实例分析
θτ(MEDV|RM,TAX,PTRATIO,LSTAT)=
g(γ1RM+γ2log(TAX)+γ3PTRATIO)+
γ4log(LSTAT).
用本文提出的方法对该问题进行估计,计算在不同分位数下系数的估计值,并采用bootstrap方法估计标准差,方法如下,具体细节可参考文献[13,29]。
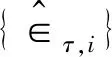
重复模拟100次计算标准差,所得结果列于表7。从表7可以发现,RM的系数在不同的分位数下皆为正,这表明每栋房屋的房间数量越多,房价就越高且收入越多的家庭更加在意每栋房屋的房间数量;log(TAX)的系数为负且随分位数逐渐变大,这表明不动产的税率越高,房价越低且收入较低的家庭更加在意不动产税率的大小;PTRATIO 的系数为负且随分位数变化较小,这表明学生与教师的比例越大,即教师资源越匮乏,房价越低且低收入家庭与高收入家庭对教育的重视程度是同样大的;log(LSTAT) 系数为负且随分位数逐渐变小,这表明一个地区低收入人群所占的百分比越高,房价越低且收入较高的家庭更加在意一个地区的低收入人群比例。
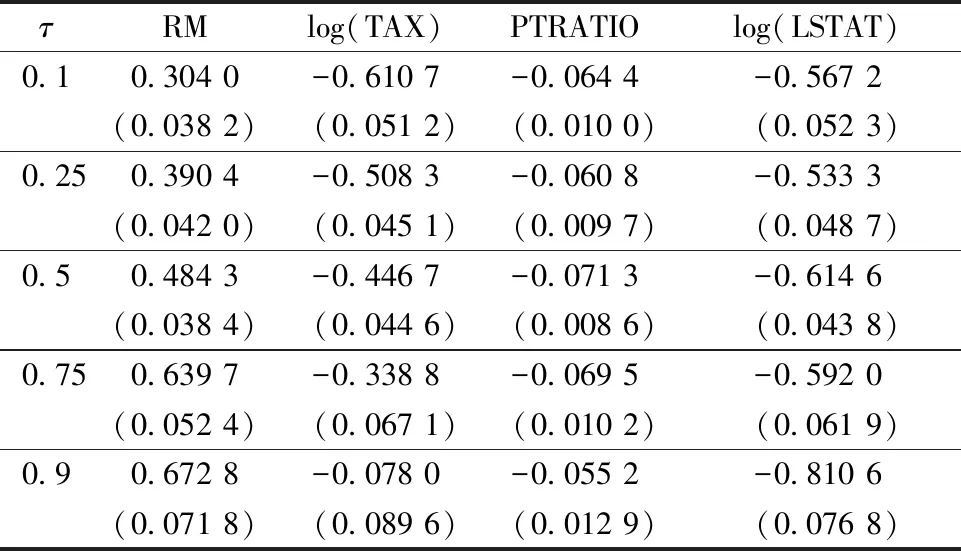
表7 波士顿数据集在单指标分位回归模型下的系数估计及标准差估计Table 7 Coefficient estimation and standard deviationestimation of Boston data set under the single-indexquantile regression mode
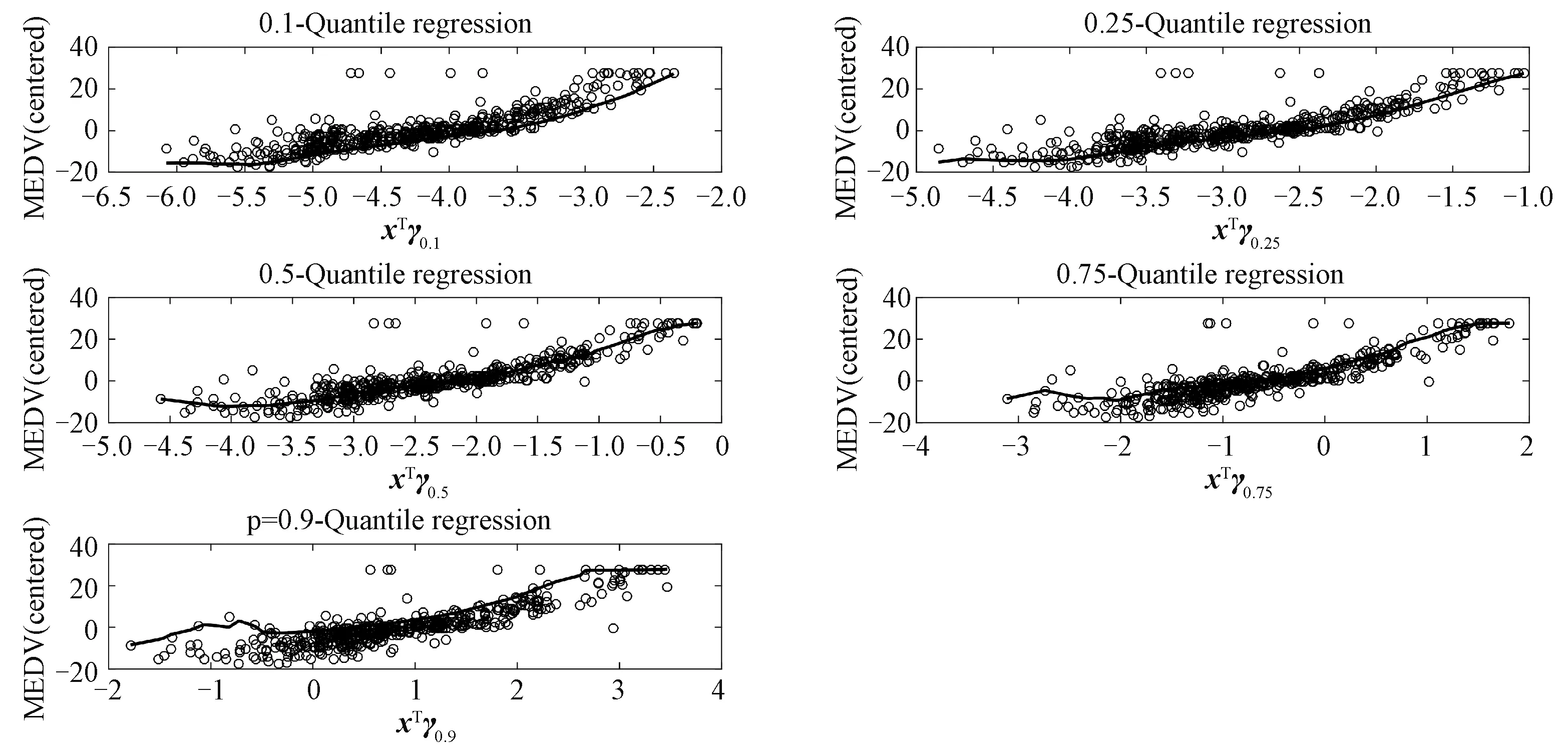
图1 联系函数g(u)及在不同的τ下,的估计Fig.1 The link function g(u) and the estimation of under different choices of τ
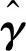
5 结论
本文研究单指标分位回归模型估计方法的MM算法。相比于内点法,MM算法极大地缩短了计算时间,提高了运算效率。此外,本文给出单指标分位回归模型在MM 算法下的参数估计公式,在每次迭代过程中,将协变量与响应变量的观测值直接代入公式,即可得到参数的估计值,避免了每次迭代都要优化目标函数的麻烦。

