粗糙集最优近似的动态更新方法

罗来鹏，范自柱

华东交通大学理学院，江西南昌 330013

粗糙集理论[1-2]是建立在集合论基础上，用来分析和处理不精确、不协调、不完备信息的数学理论，是当前3大粒计算模型之一，已被成功应用于人工智能与机器学习等领域．目标概念在近似空间上的近似表示与计算，是粗糙集理论研究与应用的基础．当目标概念无法用近似空间上基本知识粒完全定义时，一直以来都是借用拓扑中的内核和闭包概念，采用其上近似集和下近似集作为近似边界来刻画，因此，目标概念在近似空间上往往存在边界域的不确定性，进而造成系统及规则知识的不确定性.为深入挖掘及有效利用边界域信息，ZIARKO[3-4]提出变精度近似并建立变精度粗糙集模型和概率粗糙集模型，所得约简规则提高了容错性，且能将小样本数据得到的结论用到大数据中．但是，这两个模型在实际应用中存在如何优化参数阈值的问题，参数值直接影响近似集计算和属性约简结果[5]．同时，这种近似的思路仍然是从基本知识粒即等价类角度来定义目标概念的近似，并未从系统角度来看待目标概念的近似，且当目标概念是粗糙时，其近似表示仍是用它的下(上)近似集，而非一个具体的可定义的集合．为此，张清华等[6-7]以相似度为度量标准提出目标概念的最优近似，即在近似空间上所有可定义的集合中找一个与目标概念相似度最高的集合作为目标概念的近似．基于此，LUO等[8]给出了粗糙集最优近似的代数定义、计算和基于最优近似的分布约简，讨论了在相同近似空间下目标概念的最优近似与其上(下)近似之间，以及基于最优近似的分布约简与基于上(下)近似分布约简之间的关系，发现基于最优近似所建立的分布约简更能反映数据本身特性，也更能体现粗糙集应用中不需要先验知识的优势．

然而，实际应用中数据库中的数据往往是动态变化的,因此，粗糙集的动态知识发现是目前粗糙集研究的重点．当前研究主要集中在论域变化、属性集变化和属性值域变化等方面．YU等[9]针对属性集变化的区间值信息系统设计了两种动态近似计算算法； LI等[10]针对基于优势关系的动态信息系统讨论了基于对象集的变化时近似集的增量式更新方法． CHENG等[11]在模糊粗糙集中,提出了两种概念近似增量更新的动态方法．HU等[12]在多粒度粗糙集中，针对单个粒结构随时间演化，提出基于矩阵的动态近似更新方法．JING等[13]通过引入知识粒度增量机制，讨论了多个对象发生变化时，更新约简的两种增量方法． ZHANG等[14]研究了基于知识粒度的增量属性约简方法．WEI等[15]通过压缩决策表，讨论了对象集变化时动态数据的属性约简．GE等[16]讨论了基于冲突区域的增量机制，提出在新增对象情况下属性约简的更新计算方法．HU等[17-18]就多种模型，如优势关系粗糙集模型、集值粗糙集模型以及不完备系统等，讨论了近似更新等.

但是，当前关于粗糙集动态知识获取的研究更多地局限在基于不同模型目标概念的上、下近似，随着粗糙集最优近似集的提出，基于粗糙集的最优近似动态更新计算成为新的研究方向，但目前尚未见文献报道．为此，本研究针对对象集增加的情况，探讨了决策系统中各决策类的最优近似的动态变化规律，为建立基于最优近似的动态分布约简提供参考．

1 相关概念

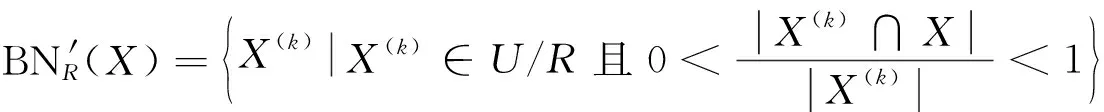
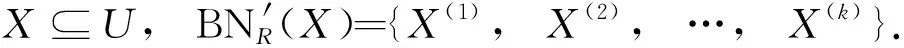
由定理1可知，计算目标概念的最优近似集的关键是需要获取两个参数值，即目标概念中正域所占的比值和目标概念在其边界类上的分布向量．

2 最优近似集更新原理与算法

2.1 最优近似集的更新原理

更新计算一直都是信息处理研究的重点和难点．在粗糙集动态知识更新内容中，对象增加是普遍情况．考虑到增加多个对象的更新操作可看成是对增加单个对象更新的递推，并且对象删除处理方法具有一定的类似性，接下来将讨论单个对象增加的情况下，决策系统中决策类的最优近似更新原理，并设计相应的算法．

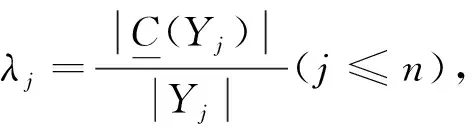
接下来针对对象集新增一个对象并引起值域发生不同变化的情况，讨论决策类最优近似更新．

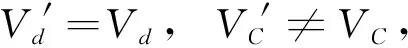
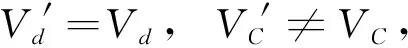
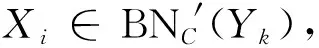
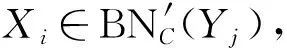
【证】

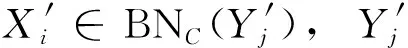
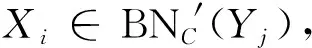
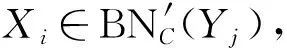
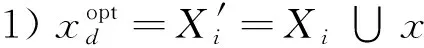
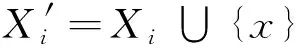
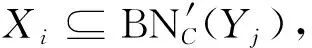
综上可见，新增一个对象后，决策系统中决策类最优近似更新的计算，只需分析变化的条件类对决策类正域、边界域和负域的改变情况．显然，与非增量计算相比，增量更新计算可极大地简化求解过程；同时，因新增对象所引起的属性值域的变化不尽相同，决策类更新的时间复杂度也未必一样．

2.2 最优近似集的更新算法描述

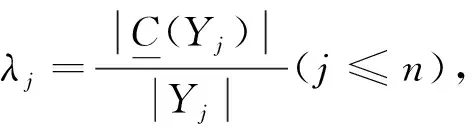
步骤2对新增数据类别进行判定，并计算决策类最优近似的更新结果．

3 实验方案及性能比较

3.1 实验方案

从UCI公用数据集(http://archive.ics.uci.edu/ml/index.php)选择数据集Zoo、Hayes-roth、Lymphography、Monk’s problems和Balance-scale，采用SQL server 2008中的SQL进行编程，测试不同条件下最优近似更新计算的运行时间．实验测试所用的计算机配置为：内存为8 Gbyte, CPU为Intel®Core(TM) i7-8550U，1.80 GHz，操作系统为Windows 10．表1为5个数据集的参数描述．

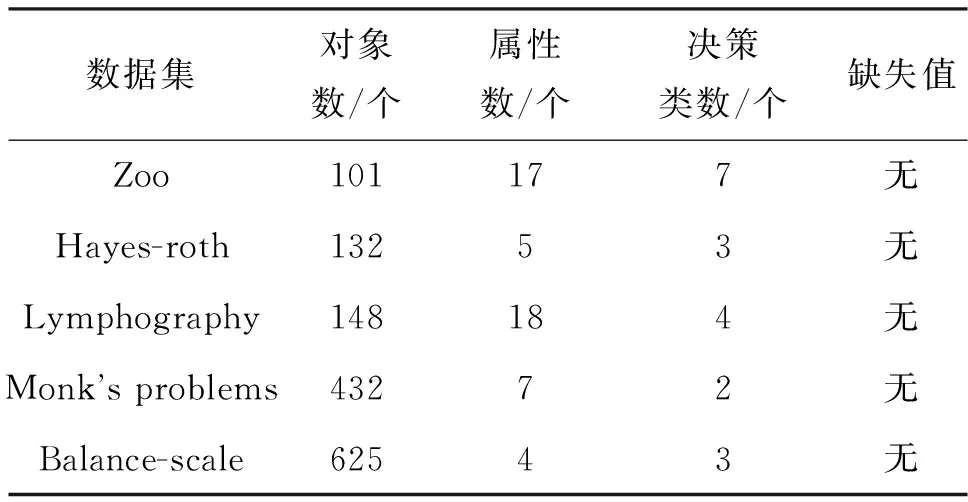
表1 数据集描述

3.2 结果与分析

图1 不同数据集在不同增量类别时的更新时间Fig.1 Update time for different categories of data on different data sets

图2 增量与非增量更新时间对比Fig.2 Comparison of incremental and non-incremental update time

图2为新增单个对象，并在不同数据集上进行增量更新与非增量更新时，求解最优近似算法的运行时间结果．运行时间取5次随机新增一个对象时的运行时间的平均值．由图2可见，利用增量更新与非增量更新方法，在不同数据集上计算最优近似的耗时并不一样，增量更新方法所需时间较少，优势明显．当数据集决策类增加且数据集中的对象数较多时，增量更新方法的耗时也会增长，但并不明显，而非增量算法的耗时却呈快速增长．可见，增量更新算法的时间效率要优于非增量更新，究其原因主要是在动态环境下，当对象增加时，采用非增量更新方法计算最优近似集需要比较每个决策类与每个条件类，造成较多重复计算，而对于增量更新方法，只需关注变化的条件类对决策类正域以及边界类分布值的影响，减少了比较次数，提高了效率．尤其是当数据集较大时，增量更新方法具有较好的时间性能，其计算最优近似集的时间效率明显优于非增量方法计算．

结 语

针对决策系统动态变化情况下，决策类的最优近似更新问题，本研究就单个对象增加引起值域发生改变的4种不同情况，讨论了决策类的最优近似的变化机制，并给出4种不同变化情形下的最优近似更新求解方法．仿真实验结果表明，所提增量式更新算法能够快速地对最优近似结果进行快速更新，具有很高的计算性能．