Taylor-Couette流动特性与减阻实验研究进展
张文云, 胡海豹, 文 俊, 曹 刚, 任刘珍
西北工业大学 航海学院, 西安 710072
0 引 言
随着能源消耗的快速增加,能源问题已经成为全球性的问题。如何实现节能降耗是目前国内外关注的重要研究课题。研究表明,船舶航行时,其表面的摩擦力可占总阻力的70%~80%,即使在高速航行情况下,也可占到大约40%[1]。海洋运输成本低廉,一直是国际物流的主要运输方式,减少船舶航行阻力可节约能源,缓解由能源快速消耗造成的能源危机,对海洋开发向深海、远海发展有重要意义。
间隙中充满流体的同轴转子可类比为流体力学中的经典Taylor-Couette流动模型。该模型具有结构简单、便于开展高精度实验测试等特点[2],常与Rayleigh-Bénard(RB)对流模型和管道流动模型[3-5]一起,用于研究不稳定性[6-7]、非线性动力学[8-9]和湍流[10-13]等经典流体力学机理问题。同时,涉及Taylor-
Couette流动的轴类零件在工程中普遍存在,相关减阻研究不仅可以应用于工程领域,也可以推广至其他流动。
研究Taylor-Couette流动的流动特性,对探索基于Taylor-Couette流动的减阻方法和减阻机理研究有重要的意义。本文系统介绍了Taylor-Couette流动的主要无量纲影响参数、流场结构与扭矩特性,总结了基于Taylor-Couette流动的减阻研究进展。
1 Taylor-Couette流动基本特征
1.1 Taylor-Couette流动的无量纲影响参数
Taylor-Couette流动模型由2个同轴旋转的圆柱组成,圆柱间充满流体,允许内、外圆柱以不同速度和旋向旋转。图1(a)为经典Taylor-Couette流动示意图,旋转圆柱间隙内一般存在成对、旋向相反的Taylor涡结构;图1(b)为Taylor-Couette流动间隙轴向速度分布示意;图1(c)为Taylor-Couette流动间隙方位角速度分布示意。影响Taylor-Couette流动的无量纲参数主要有雷诺数Re、泰勒数Ta及努塞尔数Nuω。

图1 Taylor-Couette流动示意图[2] Fig.1 The schematic diagram of Taylor-Couette flow[2]
内、外圆柱雷诺数Rei和Reo分别为:

(1)

(2)
式中,ri、ro分别为内、外圆柱的半径,ωi、ωo分别为内、外圆柱旋转角速度,d为内外圆柱间隙,ν为流体运动黏性系数。一般定义Rei为正;当内、外圆柱旋向相同时,定义Reo为正;当外圆柱静止时,定义Reo为零;当内、外圆柱旋向相反时,定义Reo为负。
为表征内、外圆柱半径和曲率的影响,引入泰勒数Ta:

(3)
式中,η=ri/ro为内外圆柱半径的比值。为表征内圆柱恒定角速度时所受的扭矩,Eckhardt等[14]定义了努塞尔数Nuω:

(4)

1.2 Taylor-Couette流动流场特性
1923年,Taylor[15]首次发现当内圆柱转速ω超过临界值ωc时圆柱间隙内流动会发生失稳,出现Taylor涡对。此后,学者们对Taylor-Couette流动的不稳定性和体系结构展开了广泛的研究。1986年,Andereck等[16]系统总结了一定Rei和Reo范围内Taylor-Couette流动的体系结构,如图2所示。2014年,Ostilla-Mónico等[17]通过DNS方法模拟更高Ta下Taylor-Couette流动,进一步扩展了其体系结构,并给出了Taylor-Couette流动的终极状态,如图3所示。从图中可见,Ta从7.04×105提升到4.63×109过程中,圆柱间隙流动会经历层流状态、过渡区和终极状态(充分发展湍流状态)。

图2 不同雷诺数条件下Taylor-Couette流动的流动体系[16]Fig.2 Flow regime of Taylor-Couette flow at different Reynolds numbers[16]
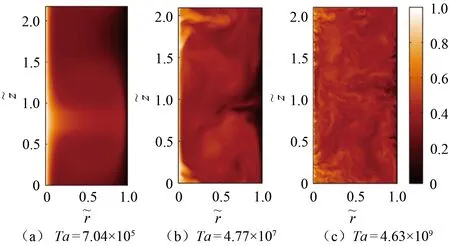
图3 高泰勒数下Taylor-Couette流动瞬时速度场[17](η=0.714)Fig.3 Flow field of Taylor-Couette flow at high Taylor numbers[17]
Taylor涡结构和流动不稳定性不仅在同轴旋转圆柱间隙流动中存在,在同轴圆锥面之间[18]、圆柱与圆锥之间[19]及同心椭球[20]之间也同样会形成不同形态的Taylor涡和流动不稳定现象,如图4所示。近年来,学者们还发现Taylor-Couette流动与对流[21-22]、黏弹性流体[23]、磁场[24]结合时,也存在有趣的流动不稳定性问题。

图4 不同几何结构下的Taylor涡的形态[18,20]Fig.4 Taylor vortex characteristic with different geometry structures[18,20]
1.3 Taylor-Couette流动的扭矩特性
Taylor-Couette流动的扭矩主要决定于Ta和内外圆柱半径比η。Ostilla-Mónico等[25]通过实验与数值模拟结合的方法,给出了不同半径比η下扭矩(Nuω)与Ta之间的标度率关系,如图5所示。在Taylor-Couette流动达到终极状态之前,Nuω∝Taα,其中指数α依赖于内外圆柱半径比η。当Taylor-Couette流动达到终极状态时,α=0.38,即Nuω∝Ta0.38。这是因为在Taylor-Couette流动的终极状态,不管是间隙的中心区域还是在边界层区域,流动均变得非常紊乱。同时,Taylor-Couette流动中不同的流动状态对应不同的标度率关系,当内外圆柱半径比η=0.714时,标度率的主要规律如下:在外圆柱静止、内圆柱转动的状态下,当边界层和间隙区域均为层流时,α=0.33;当转速继续增加,间隙中的Taylor涡开始紊乱时,α<0.33,而在流动的终极状态时,α>0.33。

图5 不同半径比对扭矩的影响规律[25] Fig.5 Torque scaling with different radii ratios[25]
2 Taylor-Couette流动减阻研究
Taylor-Couette流动的阻力为摩擦阻力,因此各种减少摩擦阻力的方法(如气泡减阻[26]、超疏水减阻[27]和沟槽减阻[28]等)都可用于减少Taylor-Couette流动内圆柱的扭矩。涉及减少摩擦阻力的减阻方法统称为Taylor-Couette流动的通用减阻方法。Taylor-Couette流动的内外圆柱之间存在成对的Taylor涡结构,是内外圆柱间动量传输的主要途径。设法降低Taylor涡引起的能量耗散,可以有效减小内圆柱的扭矩。通过减少Taylor涡对数和耗散的减阻方法统称为Taylor-Couette流动的特有减阻方法。
2.1 通用减阻方法
1)气泡减阻方法
Taylor-Couette流动中的气泡受浮力、重力和离心力的共同作用,大多数气泡会在内圆柱表面聚集分布,只有少部分气泡会和Taylor涡相互作用,被卷入Taylor涡中[26]。Murai等[29]研究了在底部通气时Taylor-Couette流动的扭矩特性和气泡行为,实验表明:通气条件下Taylor涡的波长增加了32%,而内圆柱的扭矩下降了31%,如图6(a)所示。Fokoua等[30]研究了不同雷诺数条件下气泡尺寸对减阻效果的影响规律。大多数学者认为,气泡减阻是由气泡变形[31]或其对流动结构的影响[32]导致的,研究气泡减阻机理对气泡减阻实际应用具有非常重要的意义。Berg等[33]发现转子表面粗糙时内圆柱的无量纲阻力明显高于不通气时,揭示了气泡减阻是一个纯边界层效应。Gils等[34]发现气体体积分数相同时减阻率随雷诺数增高而变高,推导出气泡变形量是影响气泡减阻的一个重要因素。Verschoof等[35]在内外圆柱流体中加入表面活性剂,减阻率由40%降至4%,表明气泡变形量对减阻效果有决定性作用。Bakhuis等[36]发现湍流时增加或减小刚性粒子尺寸会导致阻力轻微增加或减小。上述学者的研究揭示了气泡减阻机理,为气泡减阻的工程应用做出了贡献。
2) 超疏水减阻方法
受荷叶表面憎水特性启发,超疏水减阻作为新兴的减阻方法受到学者们的广泛关注。Srinivasan等[37]研究了湍流条件下超疏水表面的减阻特性,雷诺数为8×104时减阻率为22%,同时得到19 μm的有效滑移长度。Saranadhi等[38]加热超疏水表面在相对低的温度下形成稳定低温Leidenfrost表面,最高实现约90%的减阻率,如图6(b)所示。胡海豹等[39]通过在内圆柱表面构造亲疏水相间环形条带结构,得到超过70%的减阻率,如图6(c)所示。Buren等[40]在圆柱表面加工凹槽,并在凹槽中填充烷烃,形成liquid-infused表面,实现约35%的减阻率,同时还发现减阻率随黏性比、沟槽宽度、流体面积分数和雷诺数的增大而增大,如图6(d)所示。

图6 Taylor-Couette流动通用减阻方法Fig.6 Regular drag reduction of Taylor-Couette flow
3) 沟槽减阻方法
快速游动的鲨鱼皮肤在流动方向上呈现沟槽结构,这些沟槽结构在湍流状态下可减少皮肤摩擦阻力[41]。Greidanus等[42]在旋转圆柱间隙流动的内圆柱表面构筑微米级沟槽,发现雷诺数小于4.7×104时,沟槽表面有更大摩擦系数;而当雷诺数大于4.7×104时,沟槽减阻开始显现,并且雷诺数越大减阻效果越好。PIV测试表明,存在沟槽时内圆柱表面的速度梯度明显减小。但是并不是所有尺寸的沟槽都能够减少内圆柱的扭矩,Zhu等[43]发现内外圆柱表面构造的V型槽会诱导产生二次环流,导致内圆柱扭矩增大。Verschoof[44]和Zhu等[45]还发现在内圆柱外表面沿轴向布置矩形沟槽时均增大了内圆柱的扭矩。
2.2 Taylor-Couette流动特有减阻方法
1) 基于添加圆柱外筒的减阻方法
Grossmann等[46]推导了Rayleigh-Benard对流的耗散形式:
εd=εbulk+εBL
(5)


图7 Taylor-Couette流动结构减阻方法[48] Fig.7 Structure drag reduction method of Taylor-Couette flow[48]
2) 基于Taylor涡调控的减阻方法
Mullin等[49]发现当液面高度变化时可维持不同对数的Taylor涡。Mansour等[50]做了相同的工作,研究了Taylor涡拉伸、压缩时的稳定性限制,但未定量测试其减阻效果,如图8(a)和(b)所示。Martínez-Arias等[51]进一步研究发现Taylor涡对数越多,内圆柱扭矩值越大。Brauckmann等[52]通过DNS模拟,也证实了Taylor涡对数与圆柱扭矩之间的这种关系,如图8(c)和(d)所示。可见,维持较少的Taylor涡对数是旋转圆柱间隙流动的潜在减阻方法。Xiao等[53]发现一定雷诺数范围内,内圆柱旋转加速度越大,Taylor涡对数越多。除了上述2种调控Taylor涡对数的方法外,胡海豹等还发现通过在内圆柱表面构筑气环,不仅能降低Taylor涡强度,也能够减少Taylor涡对数[39];此外,Murai等[29]发现在旋转圆柱间隙流动底部通气时Taylor涡的波长也会增加。

图8 Taylor-Couette流动特有减阻方法Fig.8 Special drag reduction methods of Taylor-Couette flow
3 总结与展望
间隙之间充满流体的同轴转子在工程领域广泛存在,属于经典的Taylor-Couette流动结构。研究转子减阻技术不仅有利于减少能源消耗,而且有助于扩展对Taylor-Couette流动结构的认识和减阻机理的了解。探索高效的旋转圆柱减阻方法极富研究价值。目前仍有待加强的研究问题包括:
1) Taylor-Couette流动中气泡[34-36]和高分子减阻方法[54]的机理探索。Taylor-Couette流动结构简单、便于开展高精度实验测试,可方便高效地进行转子减阻的可视化研究。因此,利用Taylor-Couette流动可以进行气泡减阻和高分子减阻的机理测试和探索,为管道流动和其他流动提供更多的参考。
2) Taylor-Couette流动复杂流场结构的进一步认识很大程度上可以促进旋转圆柱间隙流动的减阻问题研究。比如,温度梯度[55-57]、磁场梯度[58-59]等作用下的圆柱间隙流场结构仍不清楚;间隙内充入黏弹性流体[60-61]等非牛顿流体对流场结构的影响有待揭示。
3) 基于Taylor-Couette流动的复合减阻方法有待进一步探索,现有的Taylor-Couette流动减阻方法较为单一,可开展基于Taylor-Couette流动的气泡超疏水耦合减阻方法等其他减阻方法研究。另外, Taylor-Couette流动特有减阻方法的系统研究相对较少,较低雷诺数条件下利用Taylor涡调控内转子扭矩的方法有待进一步发展。

