基于远场可变孔径的贝塞尔函数拟合法求单模光纤模场直径

胡 越，项华中，赵仁燕，涂建坤，郑 刚*

1 上海理工大学上海市介入医疗器械工程研究中心，上海 200093；

2 上海电缆研究所，上海 200093

1 引言

光纤在通信、工业工程、生物医学领域都有着广泛的应用[1-2]。随着技术的不断发展，对光纤的性能提出了更高的要求。降低光纤损耗是当前各类光纤应用中的研究重点[3]。模场直径作为单模光纤的一个重要参数[4]，由它可以导出单模光纤的连接损耗、弯曲损耗、微弯损耗以及光纤的色散等参数[5-7]。因此准确快速地测量模场直径，有助于更深入了解光纤特性，提高并保证光纤在工业工程中的应用质量。我国国标GB15972.45-2008 中对模场直径的测量给出了四种方法[8]，分别是直接远场扫描法[9]、远场可变孔径法[10]、近场扫描法[11]、光时域反射计法[12]。其中，直接远场扫描法是测量单模光纤模场直径的基准试验法。它直接按照柏特曼(PetermannⅡ)远场定义[4]，通过测量光纤远场辐射图计算出模场直径。但该方法测量动态范围大，对测量系统有较高要求，不易实现。作为第一替代方法，远场可变孔径法凭借其操作简单、测量精度高的优点而被广泛采用。近些年，熊婷婷[13]等人通过后向散射法对光纤模场直径进行测量，后向散射法主要利用常规光时域反射仪(OTDR)通过双向测量法对光纤接头损耗的精确测定以及在测试中对高阶模影响的有效控制，使其模场直径测量结果具有很好的准确性。Nakamura[14]等人通过改进的光时域计法对双模光纤的LP01和LP11模模场直径进行了测量，并通过仿真验证了其方法的有效性。Matsui[15]等人通过实验验证得出远场可变孔径法和远场扫描法均可以得出准确有效的模场直径数值。徐圣杰[16]等人发现在模场直径多次测量过程中后向散射法仍存在结果的不稳定性，仍须以远场可变孔径法测量结果为准。通过远场可变孔径法测量模场直径，需要测量一组透过不同尺寸大小孔径的光功率数据，然后由采集到的光功率数据经处理并计算得出模场直径。该方法在测量过程中，须对正光纤中心和各个透光孔中心。而在连续的电机转动测量过程中，有可能产生对正偏差，从而引起模场直径的测量误差。

本文提出一种基于远场可变孔径并通过贝塞尔函数拟合光功率分布的方法求出模场直径。通过电磁矢量在圆形光纤介质中传输的精确解(由第一类和第二类变型贝塞尔函数描述)对由远场可变孔径法采集测量出的二维远场光功率分布进行拟合，得到光纤中远场的真实模场分布曲线。再由拟合出的由贝塞尔函数表征的模场分布曲线根据柏特曼(PetermannⅡ)远场定义求出模场直径。本方法通过函数拟合的方式能有效消除远场可变孔径法中可能出现的由于光纤中心与透光孔中心不对正产生的偶发误差或其他误差，并将远场可变孔径法中计算过程的矩形近似积分替换为函数曲线积分，有效地提高了模场直径测量结果的准确性和稳定性。

2 测量原理分析

本文测量方法的基础是远场可变孔径法。将通过远场可变孔径法采集得到的不同孔径光功率数据作为原始数据，通过两段贝塞尔函数进行拟合并得到模场分布曲线，然后依据柏特曼(PetermannⅡ)远场定义式直接计算得出模场直径。将本方法的测量结果与OFM光纤多参数测试仪[17]的测量结果进行比较，从而验证本方法测量的准确性与稳定性。OFM 光纤多参数测试仪由原机械工业部上海电缆研究所(国家电缆检测检验中心)遵循我国国标GB.15972 与国际通信标准IEC 60793 的测试方法开发研制。该测试仪可以测试光纤的衰减、模场直径、截止波长等参数，是目前国内外光纤光缆研究、生产及使用等单位的常用仪器。

2.1 光纤波导的电磁理论解

光纤是一种圆形介质波导。光在光纤内传播的本质是电磁波在介质波导内的传输。光波电磁矢量的精确解根据电磁场理论经过严格的求解得到，它们满足均匀圆形介质波导边界条件的麦克斯韦方程组[18-19]。由于光在光纤中的传播方向角几乎为零，所以只要先求出光波的轴向分量就可以根据麦克斯韦方程组得到其他的横向分量。轴向场分量对应的圆柱坐标系下亥姆霍兹方程为

式中：r为距光纤中心的距离，φ为光纤端面的方向角，z为距光纤端面的距离，n为光纤的折射率，k0=2π/λ是真空中的波数，λ为真空中的波长。

为简便只分析光纤端面的分布模式。将上式变量分离，在端面上的分布规律如下式：

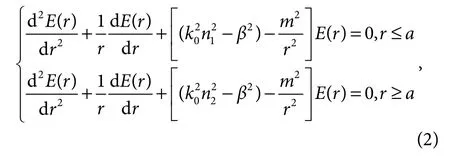
其中：E(r)为场分布，在纤芯与包层中n是不同的，n1、n2分别为纤芯和包层的折射率。对于阶跃型光纤，纤芯和包层折射率均为常数。上式是典型的贝塞尔方程，方程中的参数m为φ方向上电场变化的周期数，称为贝塞尔方程的阶，β为光纤的纵向传播常数。

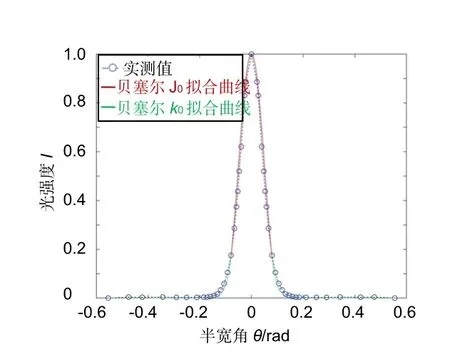
图1 为远场可变孔径法测量的远场模场分布图。在光纤纤芯区电场幅值必然是有界的，而且随r做震荡变化，因此模场的精确解在纤芯中用第一类贝塞尔函数描述。在包层区，当r趋向无穷大时，场强应趋近于零，所以在包层中用第二类变型贝塞尔函数来描述。在工程应用中也常使用其近似解高斯函数来描述场分布[20-21]，由于高斯函数具有局限性，本文将使用精确解贝塞尔函数对场分布进行描述。

通过如下两段贝塞尔函数对单模光纤模场分布进行精确描述，光强与相对半径Ra的关系为[19]

式中：Ra=r/a为归一化半径，r为光纤半径，a为纤芯半径，U为归一化横向相位参数，W为归一化横向衰减参数。U、W值均与归一化频率V值相关。

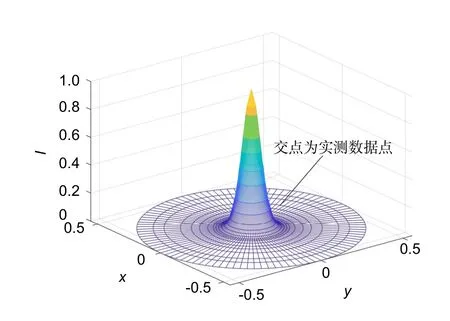
图1 实测数据模场分布图Fig.1 Mode field distribution of the measured data

式中b为归一化相位常数。

用式(3)对远场可变孔径法测量的模场分布数据进行拟合，可以得到光纤内模场分布函数，由该函数代入柏特曼远场定义式即可求得模场直径。由贝塞尔函数表示的光纤模场分布三维效果图如图2 所示。

2.2 分段拟合与模场直径的计算

根据上节，光波导在纤芯区传输用第一类贝塞尔函数J0描述，在包层中传输用第二类变型贝塞尔函数k0描述。在对远场可变孔径法采集测量的一组数据进行拟合时，应该选取合适的分段点以避免对拟合结果产生影响。由式(3)可知，在纤芯半径位置处为两段函数的分界点，其对应的光功率为

在确定了被测光纤特定工作波长下的归一化频率V值后，归一化横向相位参数U和归一化横向衰减参数W均为定值。对常用的型号为G.652 的单模光纤，在工作波长为1310 nm 时，其归一化频率V值为2.4，可得其模场分布曲线如图3 所示。

aR=1 为第一类贝塞尔J0函数曲线与第二类变型贝塞尔k0函数曲线的分段点。Ra=1 即r=a为光纤纤芯半径位置，此处对应的归一化光场强度为定值，可根据被测光纤归一化频率V值求出。对由远场可变孔径法采集的远场光功率数据进行归一化处理，得到其归一化场强值，对大于分界点的数据采取第一类贝塞尔J0函数拟合，对小于分界点的数据采取第二类贝塞尔k0函数拟合。得到两段贝塞尔函数描述的模场分布后通过柏特曼(PetermannⅡ)远场定义式由远场光功率分布确定模场直径2w0[22]。

图2 贝塞尔函数模型模场分布图Fig.2 Mode field distribution of Bessel function model

图3 G.652 光纤在1310 nm 工作波长下模场分布函数Fig.3 The mode field distribution function of G.652 fiber at 1310 nm working wavelength

式中：PF[θ]为模场分布曲线，即式(3)，θ为可变孔径半宽角。

3 测量结果与讨论

为检验本文贝塞尔函数拟合方法的测量效果，实验采用OFM 光纤多参数测试仪，对光纤型号为G.652、G.655 的常用通信光纤进行模场直径测量。OFM 测试仪对模场直径的测试性能指标如下：可测试波长1310 nm、1550 nm，重复性≤0.1 μm，最大数值孔径0.30，测试速度 2 min，所有性能指标均符合国标 GB 15972.45-2008 中的要求。该测试仪采用标准的国标中推荐的远场可变孔径法，原理图如图4 所示。光源经单色仪由注入系统进入待测光纤，旋转圆盘使光纤出射光透过圆盘上不同大小的孔径光阑，并测量通过不同孔径光阑的功率传输函数α(θ)，它是透光孔半宽角θ的函数。模场直径(MFD)为[17]

式中：

其中：P(θ) 为采集到的通过透光孔的光功率，Pmax为光纤出射总功率，x为透光孔径的半径，L为光阑孔平面与光纤端面之间的距离。

本文提出的贝塞尔函数拟合法求模场直径的计算式同式(7)，即先对同一光纤采集到的光功率离散数据通过两段贝塞尔函数进行拟合，从而得到由贝塞尔函数表征的光纤内模场分布函数PF[θ]，最后由式(7)计算出模场直径。式(7)与式(8)在模场直径的测量上具有一致性，并可以通过数学方法进行相互转换[20]。

图4 远场可变孔径法测量原理图Fig.4 Principle diagram of remote field variable aperture measurement

3.1 正常情况下光纤模场直径测量

使用G.652 单模光纤，测试波长为1310 nm，将光纤涂覆层剥离且用酒精棉擦洗干净后，安置在OFM光纤多参数测试仪的注入光纤夹上，完成校准后仪器自动有序地采集该被测光纤透过不同尺寸孔径的光功率。得到的一组实测数据如图5(a)所示，由图5(a)可见，收集到的光功率值随着孔径的增大逐渐增大，直到光功率不再随着孔径增大而继续增大(即出射光功率被完全收集)。

OFM 光纤参数测试仪将采集得到的数据通过处理后由式(8)计算得出模场直径，其中积分过程采用了GB.15972.45-2008 中建议的矩形近似积分方法，其积分函数a(θ)sin2θ～sinθ关系图如图5(b)所示。最后得到的模场直径计算结果为9.210 μm。

贝塞尔函数拟合法则将不同孔径的光功率数据处理后得到23 个模场分布离散点，使用两段贝塞尔函数对其进行拟合，其结果如图5(c)所示。实测的模场分布离散点几乎都落在拟合得到的贝塞尔函数曲线上。拟合曲线的相关系数R2接近于1 为0.9956，表示拟合优度极佳。将通过拟合得到的模场分布即两段贝塞尔函数代入式(7)，计算得到模场直径为9.208 μm，与OFM 测量仪的相对误差为0.02%。

在1310 nm 波长下，对G.652 和G.655 光纤进行了重复测量，并将两种方法的测量结果进行比较，其结果见表1。由表中数据可知，在测量条件正常情况下，贝塞尔函数拟合法与OFM 测量仪标准方法所测结果几乎相同，表明本方法具有良好的准确性。在多次测量过程中，由最大偏差数据可以看出，本方法在测量结果的稳定性(重复性)方面甚至更优于OFM 标准仪器。

3.2 异常情况下光纤模场直径测量

图5 正常情况下模场直径测量结果图。(a) OFM 测试仪光强分布图；(b) 积分函数a(θ)sin2θ～sinθ 关系图；(c) 贝塞尔函数模场分布拟合结果图Fig.5 Measurement results of modulus field diameter under normal conditions.(a) Light intensity distribution of OFM tester;(b) Graph of the integral function a(θ)sin2θ～sinθ;(c) Fitting results of Bessel function modulus field distribution

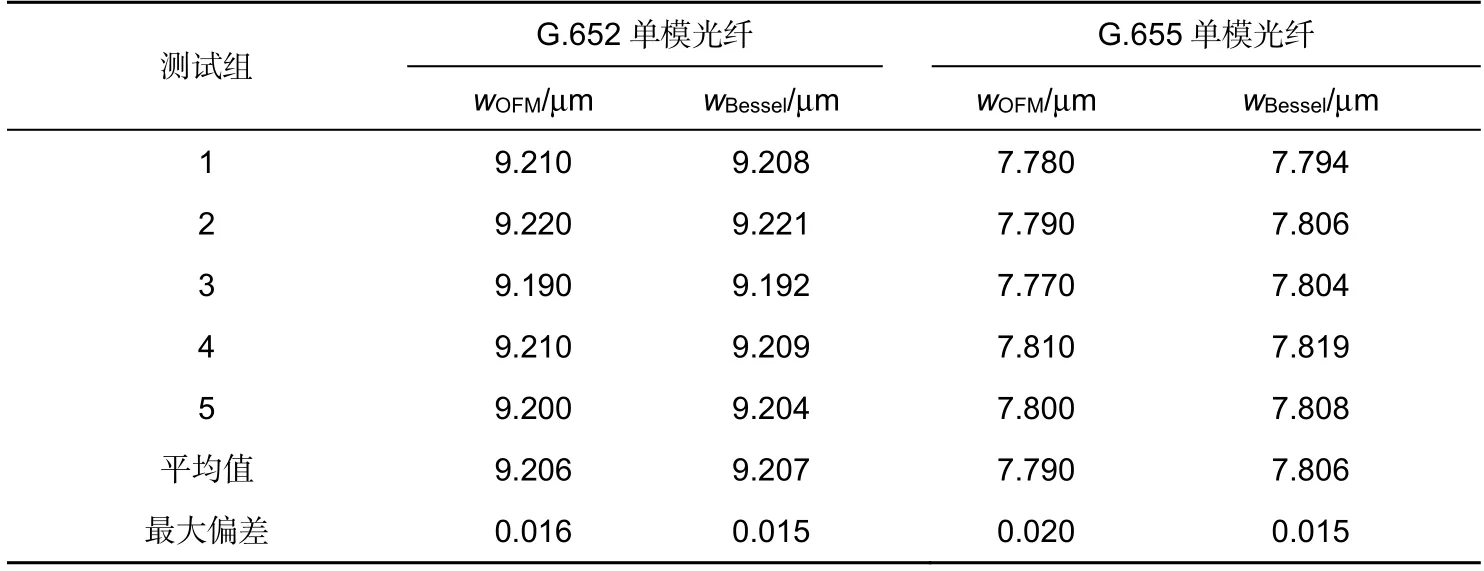
表1 在1310 nm 波长下不同型号单模光纤两种测量方法的测量结果比较Table 1 Comparison of measurement results in two measurement methods at 1310 nm wavelength

远场可变孔径法在测量过程中可能由于光纤端面切割不均匀或孔径光阑在对正过程中电机系统随机角抖动等原因导致光功率采集不完全从而使模场直径测量结果产生波动或偏离真值。

取G.652 光纤在1310 nm 波长下所测的异常数据对两种方法进行比较，该组数据中第19 个孔对应的光功率数据采集异常。

由OFM 光纤多参数测试仪得到的测量结果如图6(a)所示，由于第19 孔的光功率数据明显异常，其积分函数如图6(b)所示，由此所得模场直径的测量值为9.765 μm，相对误差6.02%，严重偏离正常值，为不可用数据，需要进行重新测量。

对同一组采集数据，通过贝塞尔函数的拟合结果如图6(c)所示，光功率分布离散点连线出现明显折线，但拟合曲线受误差数据的影响较小，由拟合曲线方程通过式(7)计算得到的模场直径为9.199 μm。相对误差0.09%，几乎不受误差点干扰，完全符合我国国标GB.15972 中规定的重复测量相对误差小于1%的精度要求。

模拟在测量过程中出现多个(孔径)误差数据的情况，并用两种方法进行测量，比较结果见表2。其中相对偏差为存在误差数据时的测量结果与正常情况的测量结果间偏差。

根据表2 中数据，OFM 参数测试仪传统方法在测量数据存在误差时，无论是对G.652 光纤还是G.655光纤，其模场直径测量结果均较大程度偏离真值；本文贝塞尔函数拟合方法则可以基本排除误差数据干扰，在两孔存在误差情况下仍然可以符合我国国标GB.15972 中规定的误差小于1%的精度要求，使模场直径测量结果的准确性得到了有效保证。

4 结论

针对单模光纤的模场直径测量，本文提出一种基于远场可变孔径法测量原理，结合光纤波导理论建立的光纤模场分布的贝塞尔函数模型，并通过此模型拟合采集到的光功率数据，得到实际的模场分布函数，最后通过模场直径定义式求出模场直径。实验表明,本方法在正常测量情况下表现出与标准仪器相当的测量准确性与一致性，而且，当测量条件变差时，本文测量方法仍可以达到国标要求的测量精度，是对国标GB.15972 中建议的远场可变孔径法测量模场直径的一种有意义的补充。同时本方法通过单个光电探测器结合可变孔径代替了价格昂贵的近红外相机，实现了近红外相机的模场获取功能，很大程度上提高了仪器的性价比。

图6 异常情况下模场直径测量结果图。(a) OFM 测试仪光强分布图；(b) 积分函数a(θ)sin2θ～sinθ 关系图；(c) 贝塞尔函数模场分布拟合结果图Fig.6 Measurement results of modulus field diameter under abnormal conditions.(a) Light intensity distribution of OFM tester;(b) Graph of the integral function a(θ)sin2θ～sinθ;(c) Fitting results of Bessel function modulus field distribution

表2 在1310 nm 波长下存在误差情况两种测量方法的测量结果比较Table 2 Comparison of measurement results of the two methods in case of error at 1310 nm wavelength