面向整车虚拟匹配的柔性件公差实时分析

邵俊 于兴林 冯波 丁华

（吉利汽车研究院（宁波）有限公司，宁波315336）

1 前言

整车虚拟匹配作为快速展示、诊断整车外观匹配状态并指导零部件修模的开发工具，其重要性近年来在汽车行业内得到了普遍的认识[1-2]。为达成提升整车外观匹配精度的核心价值，总成尺寸匹配状态计算和零部件尺寸偏差源识别是虚拟匹配的关键功能。

基于外观件普遍非刚性的特点，整车虚拟匹配需准确仿真柔性件受力变形。有限元分析法作为汽车工程主流的数值分析手段，可准确预测整车虚拟匹配尺寸状态[3]。但有限元法计算量大、求解耗时，无法满足当前数字化连接制造环境下几何保证和偏差管理的快速响应需求。为此，虚拟分析须积极利用数字化双胞胎、大数据等新支撑技术的发展[4]，开发应对实时数据的简化模型或简化求解法，突破制约虚拟匹配应用于生产现场的速度瓶颈。

在获取总成尺寸匹配状态后，为指导零部件修模，需识别零部件的偏差源变形模式。主成分分析作为汽车制造中主流的数据特征提取统计方法，可识别数据的主要模式。但由于主成分是原始变量的线性组合，鉴于汽车柔性件的监控变量较多，这种线性组合较复杂，导致可解释性差，不利于偏差源的识别。为此，需寻求简化的特征提取法，提升虚拟匹配中的零部件偏差源识别效率。

目的之一是针对汽车柔性件公差分析中缺乏快速计算带尺寸偏差零件的受力变形问题，提出1种结合线性叠加原理和有限元法的变形计算方法，实现整车虚拟匹配的实时公差分析，这部分研究工作将体现在第2节中。目的之二为解决零件偏差源识别中主成分分析数据解读性差的问题，提出1种应用稀疏主成分分析简化分析变量，并减少主成分载荷系数的偏差源统计分析法，可快速识别偏差源的主要变形模式及对应的主导变量，实现整车虚拟匹配问题的快速诊断，这部分研究工作将体现在第3节中。

2 汽车柔性件虚拟匹配实时公差分析

2.1 汽车柔性件受力分析

汽车柔性件的尺寸匹配状态主要受重力和对手件的载荷反力影响，前者可通过测量包含在测量数据中，而载荷反力必须依赖实物装配或仿真。由于来自对手件载荷反力通常为变力，如密封条、气撑杆、卡扣等，其本质是弹簧。以车门密封条为例，其压缩反力本质是个非线性弹簧，弹簧刚性系数随压缩量而变化[5]。由于性能曲线靠近设计名义值的区段接近直线，为便于简化计算，将此段的密封条刚性系数视为常数。将车门钣金总成通过铰链和锁扣安装上车身固定后，其受密封条变形后的静力平衡状态若用有限元法进行建模，则可以采用公式（1）表征。

将公式(1)整理，可得公式（2）和公式（3）。

式中，([Ks]+[Ka])-1为([Ks]+[Ka])的逆矩阵，设{}A=([Ks]+[Ka])-1{Fs}，[]B=([Ks]+[Ka])-1[Ks]，则公式(3)整理为公式（4）。

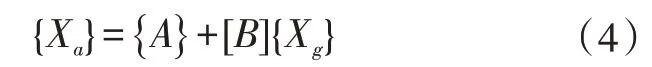
当门钣金总成无尺寸误差时，{Xg}为0，{Xa}为定值，仅受[Ks]、[Ka]和{Fs}影响。

当门钣金总成有尺寸误差时，{Xg}不为0，{Xa}为变值，与{Xg}有线性关系。

当对理论数模进行有限元建模时，由于{Xg}为0，因此{Xa}为定值。当获取1个车门钣金总成的尺寸测量样本时，由于必然存在制造尺寸误差，因此{Xg}不为0，{Xa}为变值，需要按照公式（4）调用有限元求解器进行求解。

2.2 线性叠加原理

考虑到任意线性关系均适用于线性叠加原理[6]，因此公式（4）中的任意{Xg}对应的响应{Xa}等效于将{Xg}分解为若干单位偏差向量后，所有单位偏差向量对应响应向量的矢量和。

将前述内容表示为数学关系，则设{Xg}n、{Xa}n、{Fs}n为n维列向量，表示车门有n处网格节点受密封条压缩反力作用，存在内间隙尺寸偏差，并在受载后产生变形。[Ks]与[]Ka为n阶方阵。根据向量的表示规则，将向量{Xg}n改写为公式（5）。

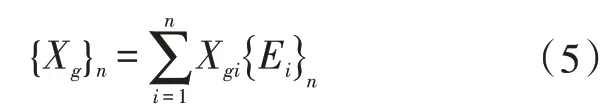
线性叠加原理应用于公式（4），并将公式（5）代入，则公式（4）可表示为公式（6）。

式中，[Xgi]nXn为n阶纯量矩阵，其主对角线元素均为Xgi，其余位置元素均为零。

根据公式(6)，只要通过有限元软件将单位偏差Ei施加于节点i（i=1…n），可求得所有n个节点的变形向量。因此通过n次迭代，可得到所有单位节点偏差与n个节点变形的关系。

2.3 基于有限元线性叠加的变形计算方法

事实上，根据公式(6)得到的变形位置是密封条，而车门虚拟匹配更为关注的区域是门周边的间隙和面差，因此若车门周边共有m处受关注的外观匹配断面，则这些断面受密封条压缩反力后的变形向量为( )C1j C2j…Cmj，m为外观匹配断面数量，Cij(i=1…m)为通过有限元法计算得到的j节点位置的单位偏差导致的i断面处的变形，因此Cij表示了i节点对j节点位移的传递系数。

当密封条变形非单位偏差，且密封条所有断面位置的偏差线性叠加时，车门周边m处受关注断面的变形总量为向量{X}m，同时如公式（7）所示。

当车门总成变形较小，即Xgj较小时，材料的应力应变处于线性段，上述公式（7）一直成立。

通过n次有限元迭代计算，即通过密封条n个断面的单位偏差仿真计算得到上述传递系数矩阵后，就可以应用此矩阵快速的在现场预测车门钣金总成受密封条压缩反力的变形尺寸状态。

只要通过测量手段获取钣金车门总成与侧围的内间隙偏差向量，即密封条各断面压缩量的偏差值向量{Xg}n，通过公式（7）的矩阵运算即可得到外观匹配断面的变形向量{X}m。而有限元法则必须根据各密封条匹配断面的尺寸偏差测量值转换为实际载荷，然后修改仿真模型的载荷边界条件，最后利用求解器计算受载变形并手工采集所有外观匹配断面的变形量。表1对比了利用纯有限元法和传递系数矩阵法计算对资源的要求，显然后者更经济高效，有助于突破制约虚拟匹配应用于生产现场的速度瓶颈。

表1 预测方法的资源要求对比

2.4 实时公差分析实例计算

2.4.1 问题定义

分析案例为采用点焊与包边工艺制造的车门钣金总成，关注其在受密封条压缩反力后的变形。实例的几何与材料属性、板件连接设置、约束边界条件见参考文献[7]。已知密封条刚度系数为每100 mm长度4 N/mm，因此在有限元模型的密封条安装截面每间隔100 mm设置一处载荷，合计38处。密封条匹配断面尺寸偏差状态如图1a所示，结合刚度系数可得到外力边界条件。同时，门框轮廓均匀布置了9处变形测点，位置如图1b所示。

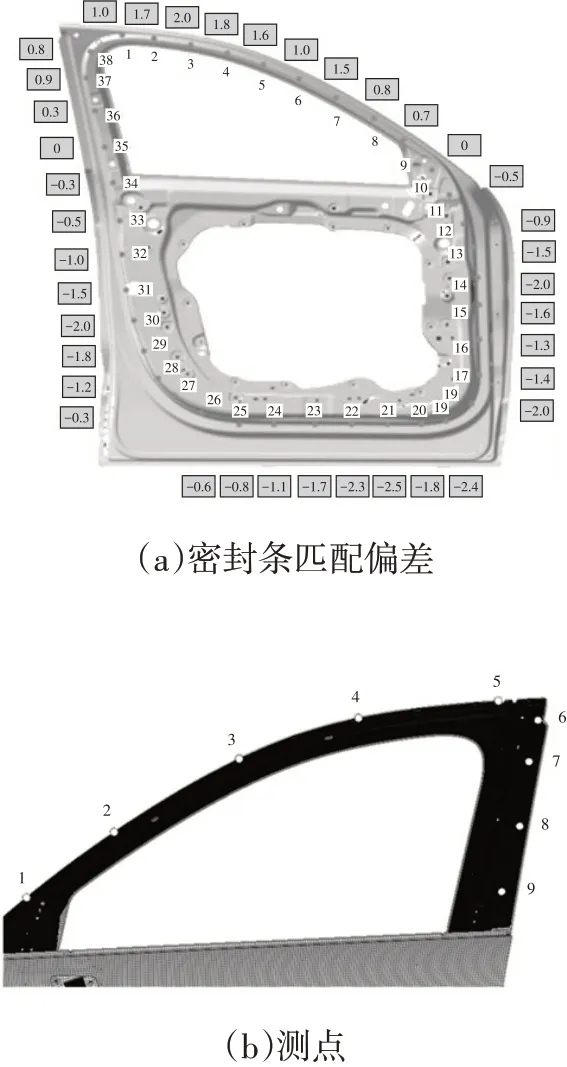
图1 密封条匹配偏差状态和测点位置示意

2.4.2 传递系数推导

根据前文传递系数矩阵的定义，此实例需推导1个9×38的矩阵矩阵的每列Cij表示通过有限元法计算得到的j节点(j=1…38)处单位载荷导致的i测点(i=1…9)处的变形。由于整车匹配的常见最小单位是0.1 mm，根据密封条刚度系数4 N/mm，因此单位载荷设置为0.4 N。通过在Hy⁃permesh中设置38个载荷步并用Optistruct求解器计算，汇总得到传递系数矩阵，如表2所示。

2.4.3 公差分析仿真结果

a.纯有限元法，根据2.4.1节的问题定义，直接采用Optistruct求解器计算得到图2的计算结果。

表2 传递系数计算结果

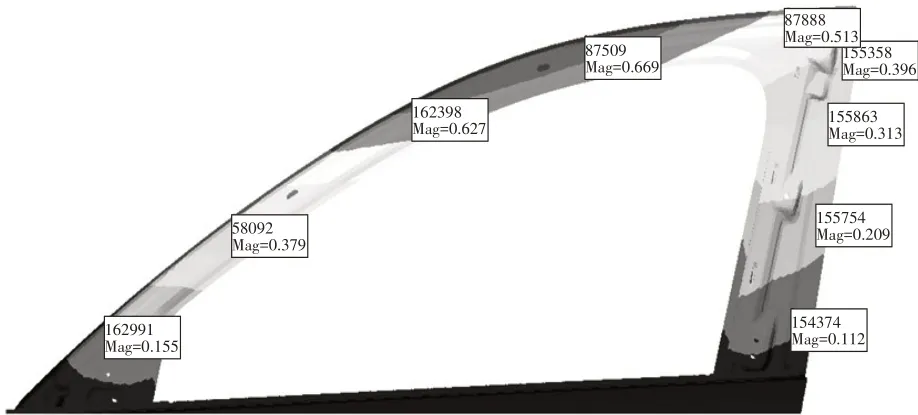
图2 有限元仿真结果

3 基于稀疏主成分的虚拟匹配问题快速诊断

3.1 虚拟匹配偏差源统计分析

汽车柔性件经过多道工序的加工，必然存在累计误差。即使在制造现场对每个样本均采用传递系数矩阵法快速计算受力变形，由于样本偏差的随机性，导致各样本虚拟匹配仿真结果存在差异，无法直接指导修模，因此有必要寻找偏差源的统计规律。

在生产中常用的变量统计指标为均值和标准差，分别体现了偏差的集中性和离散性。若生产统计受控，可将样本各变量均值输入虚拟匹配仿真模型，仿真结果可作为指导修模的参数。但当变量标准差过大时，仅靠修模无法达到匹配合格率要求，为此需识别变量波动的偏差源并进行工艺整改。

图3 传递系数矩阵法计算结果

公差分析通常假设变量间相互独立，均值和标准差均未考虑测点变量间的相关性。但相关研究显示柔性钣金不符合变量独立性假设[8]。从汽车柔性钣金件的连接工艺分析，随着点焊数的增加，焊点间距变小，独立性假设将迫使几何上相邻测点往反方向运动，这显然与焊点增多导致的刚性增加矛盾。统计学中将多变量的相关特性用协方差描述，上述源自材料弹性耦合的相关性称为材料协方差。

Merkley的研究[9]指出，由于零件表面特征的连续性，在非微观尺度，存在如图4的连续性特征，这种统计上变量间的相关性称为几何协方差。当表面两端产生了变形δ1和δ2，零件倾向于按第1种情况连续性扭曲。汽车柔性件的尺寸测量属于宏观尺寸，因此测量结果也倾向于第1种情况。

图4 由于表面连续性产生的几何协方差

3.2 主成分分析

基于上述材料协方差和几何协方差，可运用多元统计中的主成分分析法解释偏差源测量信息，即从原始变量中导出若干主成分，使它们尽可能多地保留原始变量的信息，且主成分间互不相关[10]。若运用在尺寸偏差分析领域，则每个主成分对应零件的某种偏差模式，如平移、旋转或扭曲。

主成分分析有利于抓住零件变形的主要模式，忽略占比小的随机波动噪声，实现测量数据降维的目的。例如1个柔性零件原本有几十个测点变量，通过多样本的主成分分析，可识别零件的主要偏差变形模式，用若干个变形模式包含原零件90%以上的变形信息。

按主成分定义，它识别多变量向量空间中数据方差最大的方向作为第一主成分，并按各主成分正交的原则依公差贡献排序依次计算其它主成分，n个变量可计算n个主成分。若m个主成分（m≤n）可表示零件90%的偏差信息，则前m个主成分向量PCm表示为公式（8）。

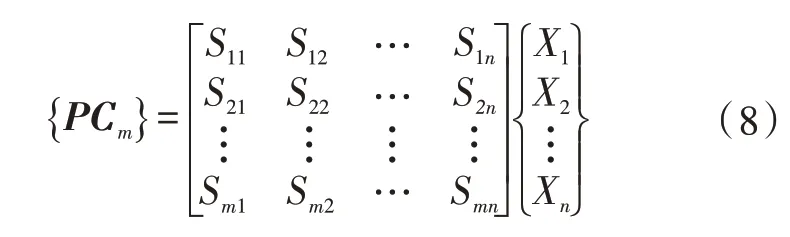
式中，Xj（j=1…n）为原始变量构成的向量；Sij表示第j个（j=1…n）原始变量对第i个（i=1…m）主成分的载荷，即影响程度系数。上述向量是对样本多变量的相关系数矩阵进行主成分分析后得到的特征向量i，表示零件的1种偏差模式。计算中同时会得到特征值λi，代表此偏差模式的方差。

3.3 稀疏主成分分析

主成分分析虽可以达到数据特征提取和变量降维的目的，但由于主成分是原变量的线性组合，当变量数量众多时，线性组合的载荷Sij数量较多，即线性组合的复杂性过高。另外，有相关研究[11]论证了在多变量和小样本的情况下，样本估计的第一主成分特征向量和总体的第一主成分特征向量极不一致。而在汽车制造业领域，小样本多变量是工业4.0环境下快速响应面对的普遍挑战，因此需更优化的方法。

基于弹性网约束改良后的稀疏主成分分析法，通过可调约束将部分载荷系数变为0，达到稀疏载荷的目的[12]。这有助于分析者在载荷系数数量和偏差信息完整度中寻求平衡，既保留了主成分分析降维的优点，又减少了主成分的构成变量数，令解读主成分的物理含义变得更容易。以虚拟匹配为例，若原始n个偏差变量需要m个主成分（m＜n）进行降维处理，由于每个主成分由n个变量线性表示，此线性变换的物理含义难以解读。若通过舍弃小部分信息使得主成分构成变量数显著减少，则有利于理解变换的物理含义，即识别尺寸的偏差模式。这有助于虚拟匹配问题的快速诊断。

深入分析载荷稀疏化的各类数学工具[13]，如制定1个强制置零的阈值或将稀疏值限定为0、-1、1，综合考虑计算速度与问题的普适性[14]，最终应用集成在R软件[15]的ElasticNet扩展包作为稀疏主成分分析的工具。R软件作为开源跨平台的数学计算环境，集成大量科研前沿的统计算法包，且数据可视化方面丰富的生态也有助于洞察数据的本质。

3.4 虚拟匹配问题快速诊断实例计算

3.4.1 问题定义

分析案例为车门钣金总成的尺寸制造偏差。测量对象为门内板密封条匹配部位的轮廓度，共19个测点，位置如图5中按顺时针分布。根据门总成的制造工艺，假定测点相关的制造误差包括门内板冲压误差2项和焊接变形误差6项，均符合正态分布。使用3维公差分析软件3DCS仿真上述误差，分布位置如图6所示。其中冲压误差2为随机误差，涉及的各区域尺寸波动独立，其余7个误差为相关性公差，涉及的各区域尺寸波动正相关。

图5 测点分布

3.4.2 基于主成分分析的公差分析

应用3DCS的蒙特卡洛法按上节所述的输入公差仿真，得到100个样本，各含19个变量的测量值。

使用R软件的基础函数prcomp对样本进行主成分分析，得到图7的主成分累计贡献度信息。

图6 制造公差信息

图7 主成分分析累积贡献度信息

前8个主成分累计方差贡献度93.0%，即可代表原始19个变量93%的总成偏差信息，降维效果显著。

由于前2个主成分累积方差占比较高（60%），可进一步采用R语言的数据可视化工具包ggbiplot对第1和第2主成分作散点图，分别对应图8中的横坐标与纵坐标。图中的点代表样本，椭圆代表按±2σ置信区间设置的核心区域。箭头代表原始变量，共19个，箭头长度表示原始变量的方差大小，箭头方向表示与各主成分的相关性。

图8 第1和第2主成分散点

为优化整改匹配问题，需识别对第1及第2主成分起主导作用的变量。由于近一半箭头对横坐标的投影长度接近，难以识别主导性影响变量，给整改带来了较大困难。第2主成分也存在相似的现象，其根本原因在于各主成分中的非0载荷过多。

3.4.3基于稀疏主成分分析的公差分析

为了将主成分的载荷稀疏化，应用R软件的spca()函数，得到图9的稀疏主成分贡献度信息。前8个稀疏主成分累计贡献度78.1%，即可代表原始19个变量超过78%的总成偏差信息。

图9 稀疏主成分分析贡献度信息

通过表3比较可见，前8个稀疏主成分对应的非0载荷数量合计21个，相比主成分分析前8个主成分的152个载荷数大幅减少。此外，简化后的载荷直观显示第1主成分主要涉及原始变量1～5，对应图5的门框。由于载荷系数接近，此偏差模式为局部移动。第2主成分涉及原始变量16～17，对应于图5的门锁区域，偏差模式也为局部移动。更重要的是，由于第1和第2主成分的主导变量明确，解释性较好，可进一步针对性排查测点相关的工位和工艺环节，实现虚拟匹配问题的快速诊断，有助于问题整改。

4 结论和展望

4.1 结论

a.通过结合线性叠加原理和有限元法的传递系数矩阵法，可快速计算带尺寸偏差汽车柔性件的变形。通过实例证明方法的有效性，为整车虚拟匹配的生产线实时公差仿真提供了1种解决方案。

b.通过基于稀疏主成分的偏差源统计分析法，可从样本数据中快速识别占主要作用的变形模式及对应的稀疏化的主导变量，提升了偏差源物理意义的解读能力。通过实例证明方法的有效性，为整车虚拟匹配零部件尺寸偏差源的快速诊断提供了1种解决方案，有利于整车虚拟匹配状态的高效整改。

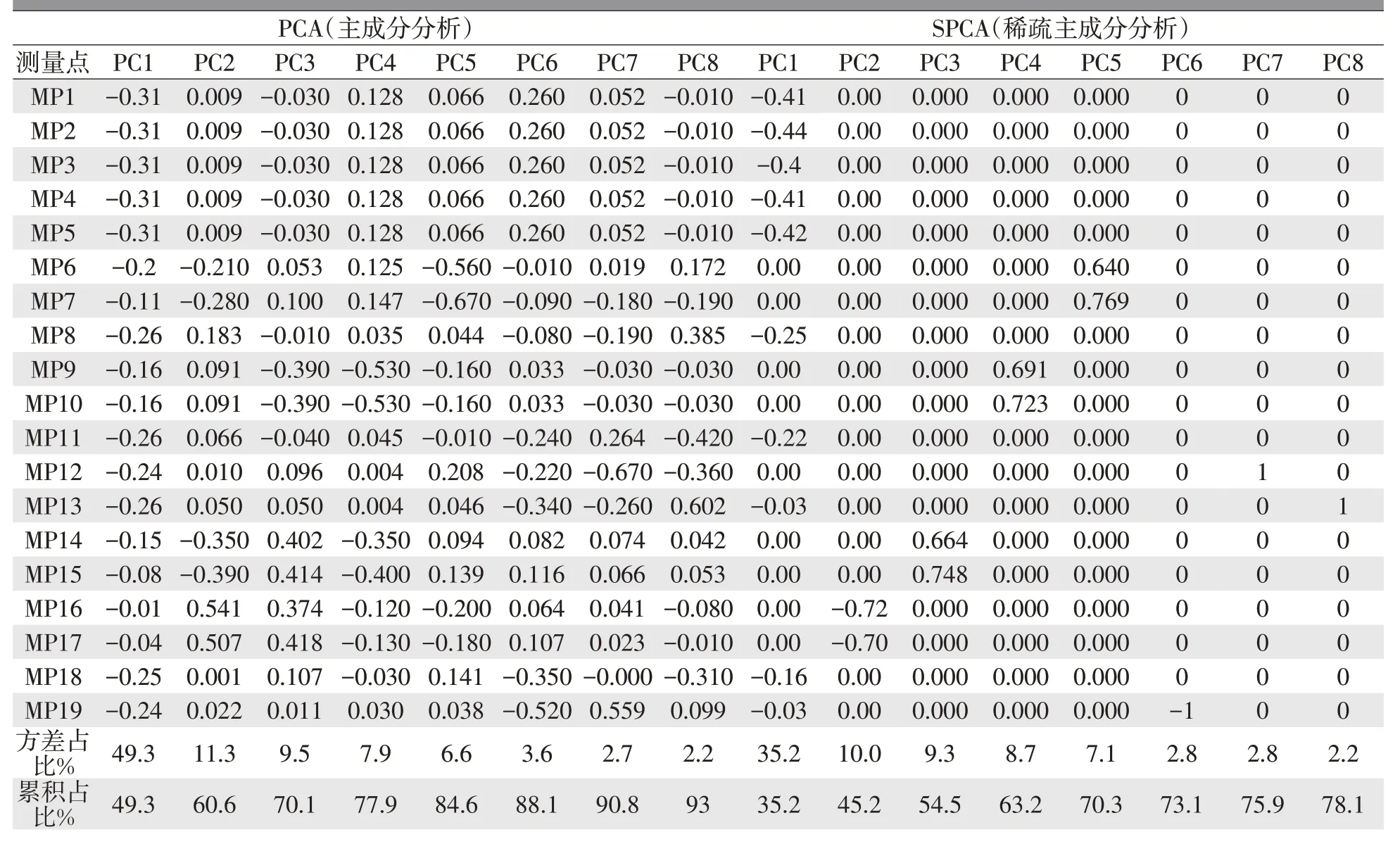
表3 主成分分析和稀疏主成分分析载荷系数对比

4.2 展望

a.传递系数矩阵法中传递系数的获取需耗费一定的有限元建模、求解计算和后处理时间，有必要通过流程梳理和软件二次开发提高这部分工作的自动化效率，进一步降低此方法的应用门槛。

b.结合聚类分析和稀疏主成分分析，实现样本分类，并分析变量随时间的变化特征，将有助于虚拟匹配整改阶段偏差源的动态诊断和监控。