铁路无缝线路极限状态法和容许应力法设计对比研究
尹银艳
(1.中铁第四勘察设计院集团有限公司,武汉 430063; 2.铁路轨道安全服役湖北省重点实验室,武汉 430063)
美国、日本、俄罗斯等国家和欧洲以及我国建筑、公路、港口、水利水电等行业的结构设计规范,均采用以概率论为基础的极限状态法,概率极限状态法是工程结构设计方法的发展趋势[1-7]。为适应铁路轨道技术的不断发展,实现与国际接轨,进一步提高铁路轨道设计的科学性,规范的计算理论从容许应力法向极限状态法转轨是十分必要的[8-12]。自2011年开始,原铁道部和铁路总公司相继主持开展了铁路工程结构设计标准由容许应力法向极限状态法转轨的基础研究工作,于2015年颁布了Q/CR 9130—2015《铁路轨道极限状态法设计暂行规范》[13](以下简称“《暂规》”)。由于《暂规》发布时间很短,且由于是与现行设计规范并行,所以广大铁路工程设计人员对其关注度不高,对极限状态设计法理解不深[8]。2018年正式发布Q/CR 9130—2018《铁路轨道设计规范》(极限状态法)[14](以下简称“《新规》”)。
本文针对福平铁路闽江特大桥(68+128+68) m连续梁,分别采用《新规》中的极限状态法和TB 10015—2012《铁路无缝线路设计规范》[15](以下简称“《现规》”)中的容许应力法对桥上无缝线路进行设计计算,对比两种设计方法检算结果的主要技术指标。同时从福平、宁安、郑万、商合杭、合福等铁路选取多个桥上无缝线路设计工点,通过对比两种方法的检算结果,分析《新规》极限状态法对无缝线路设计的影响。
1 闽江特大桥无缝线路工点概况
福平铁路闽江特大桥(68+128+68) m连续梁位于DK15+210.248~DK16+088.046处,福州端位于直线,平潭端位于R-1 600 m的曲线上,桥上采用有砟轨道,桥梁桥跨布置见图1。以下采用《新规》中的极限状态法进行无缝线路设计。

图1 闽江特大桥桥跨布置示意(单位:m)
2 计算模型及参数
2.1 计算模型
桥上无缝线路纵向附加力计算采用梁轨相互作用的有限元分析模型[16-20],如图2所示。由于扣件阻力为非线性,计算轨道应力需要进行一系列的非线性分析,采用ANSYS通用软件进行梁轨相互作用分析。
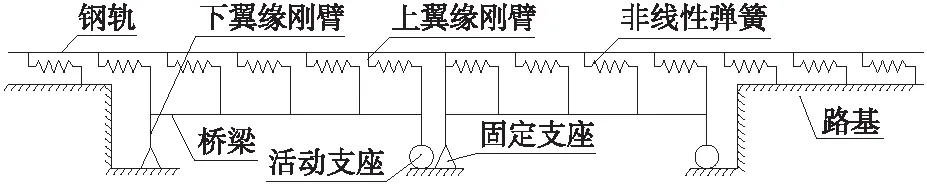
图2 梁轨相互作用计算模型
2.2 计算参数
(1)钢轨参数
福平铁路钢轨采用60 kg/m、100 m定尺长U75V无螺栓孔新钢轨。60 kg/m钢轨的截面特性如下:面积A=77.45 cm2;转动惯量I=3 217 cm4;弹性模量E=2.1×105MN/m2,钢轨钢的线膨胀系数α=1.18×10-5/℃。
钢轨屈服强度标准值按《新规》第4.2.3条规定取σs=472 MPa。
(2)钢轨温度
闽江特大桥所在区段最高轨温61.7 ℃,最低-1.7 ℃,设计锁定轨温31 ℃。
(3)线路纵向阻力
采用新Ⅲ型桥枕,有砟轨道采用常阻力扣件时,线路阻力取道床阻力;采用小阻力扣件时,线路阻力取扣件阻力。单位长度道床纵向阻力见《新规》第4.2.5条规定。
有砟轨道采用弹条V型小阻力扣件、扣件节点间距为600 mm时,车辆下或者无载时纵向阻力取值8 kN/m/轨,机车下单位长度纵向阻力取值12.4 kN/m/轨。
(4)梁温差
有砟轨道梁温差取15 ℃。
(5)列车荷载
福平铁路闽江特大桥位于福州至福州南区间,区段内为客运专线,列车荷载取CH3动车组荷载,轴重为17t,轴间距为2.5 m。
采用极限状态法设计时,《新规》中关于无缝线路计算模型及参数取值的相关规定与《现规》一致。
3 桥上无缝线路设计
闽江特大桥(68+128+68) m连续梁考虑设置小阻力方案:连续梁桥上距连续梁梁端50 m范围铺设新Ⅲc型桥枕(1 667根/km)及其配套弹条Ⅴ型小阻力扣件,其余地段铺设新Ⅲ型桥枕(1 667根/km)及其配套弹条Ⅱ型扣件。按照以上设置小阻力扣件、不设伸缩调节器方案,计算无缝线路纵向力。
3.1 轨道附加力计算
福平铁路闽江特大桥钢轨伸缩力计算结果如图3所示,钢轨伸缩力最大值为469.8 kN,换算应力为60.7 MPa。
钢轨制动力计算结果如图4所示,最大值为370.2 kN,换算应力为47.8 MPa。

图3 钢轨伸缩力
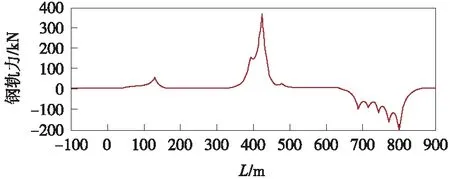
图4 钢轨制动力
3.2 钢轨动弯应力计算
钢轨在车轮动荷载作用下的钢轨动弯矩计算
Md=M0(1+α+β)
(1)
式中,M0为钢轨截面的静弯矩;α为速度系数;β为偏载系数。
轨底边缘最大动弯应力为
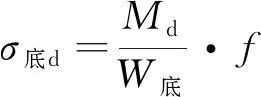
(2)
式中,Wg为轨底的截面参数,cm3;f为轨道横向水平力系数。
对于钢轨动弯应力计算中的速度系数、偏载系数和横向水平力系数,《新规》与《现规》规定取值一致。经计算,福平铁路闽江特大桥钢轨轨底动弯应力σ底=141.5 MPa。
3.3 极限状态法检算
(1)钢轨强度承载能力极限状态
无缝线路承载能力极限状态设计按式(3)进行钢轨强度检算,并按式(4)计算温降限值。
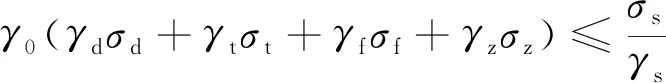
(3)
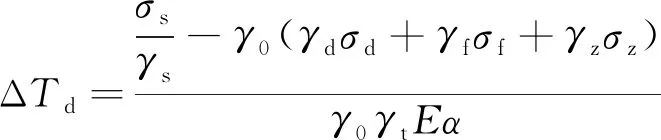
(4)
式中,γ0为结构重要性系数;σd和γd分别为轨底边缘动弯应力的标准值和分项系数;σt和γt分别为钢轨最大温度应力的标准值和分项系数;σf和γf分别为钢轨最大附加应力的标准值和分项系数;σz和γz分别为钢轨牵引(制动)应力的标准值和分项系数;σs和γs分别为钢轨屈服强度的标准值和分项系数;E为钢轨弹性模量;α为钢轨线膨胀系数。
将福平铁路闽江特大桥无缝线路纵向力计算结果代入式(4),得到温降限值为46.45 ℃。初步定的设计锁定轨温为31 ℃,锁定轨温范围为(31±5) ℃,则最大温降幅度ΔTdmax=31+5-(-1.7)=37.7 ℃<46.45 ℃,即最大温降幅度小于温降限值,无缝线路钢轨强度满足要求。
(2)钢轨断缝
无缝线路承载能力极限状态设计按式(5)进行钢轨断缝检算。

(5)
式中,λ为钢轨断缝,F为钢轨断面面积,r为线路纵向阻力,取小阻力扣件阻力值。
按上式计算得断缝40.2 mm<λ0=70 mm,故断缝检算满足要求。
(3)无缝线路稳定性正常使用极限状态
无缝线路正常使用极限状态设计按式(6)进行无缝线路稳定性检算,并按式(7)计算温升限值。
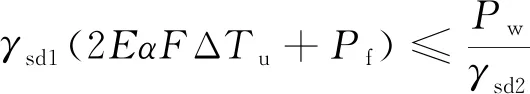
(6)
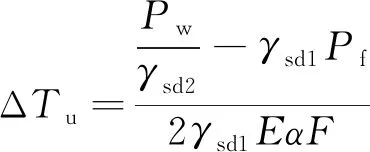
(7)
式中,γsd1、γsd2为计算模型不定性系数;Pw为临界温度压力;Pf为单线伸缩力或挠曲力的最大值。
首先,根据《新规》附录B计算出温度压力Pw=3 993.955 kN。代入式(7)计算得温升限值54.8 ℃。
设计锁定轨温为31 ℃,锁定轨温范围为(31±5) ℃,则最大温升幅度ΔTumax=61.7-(31-5)=35.7 ℃<54.8 ℃,最大温升幅度小于温升限值,故无缝线路稳定性检算满足要求。
3.4 容许应力法检算
(1)钢轨强度
容许应力法计算,钢轨附加纵向应力取伸缩应力或挠曲应力的最大值,即纵向附加力=(469.8+370.2)/77.45×10=108.457 MPa,而钢轨轨底最大动弯拉应力为141.5 MPa。故钢轨容许应力[σ]=σs/1.3=363.08 MPa。
按式(8)确定允许温降

(8)
将钢轨应力代入式(8)得到允许温降为45.7 ℃,最大温降幅度Tdmax=37.7 ℃<45.7 ℃,故无缝线路钢轨强度满足要求。
(2)无缝线路稳定性
计算得临界温度压力Pw=3 993.955 kN,则两股钢轨的允许温度压力[P]=Pw/1.3=3 072.273 kN。
按式(9)确定允许温升
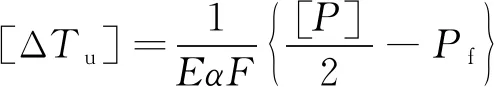
(9)
将钢轨应力代入式(9)得到允许温升为55.6 ℃,最大温升幅度ΔTumax=35.7 ℃<55.6 ℃,故无缝线路稳定性检算满足要求。
(3)钢轨断缝
钢轨断缝可按式(10)检算

(10)
按上式计算得断缝40.2 mm<λ0=70 mm,故断缝检算满足要求。
3.5 两种方法主要技术指标对比
本桥无缝线路检算的主要技术指标为容许温升和容许温降、断缝值,如表1所示。对于温升,极限状态法较容许应力法的温升容许值相差-1.4%;而温降方面,极限状态法较容许应力法的温升容许值相差1.6%;断缝检算相同。由此引起的桥上铺设方案没有变化,均在连续梁及两侧各两跨简支梁铺设小阻力扣件即可,即桥上的轨道工程数量没有变化。

表1 福平铁路闽江特大桥(68+128+68) m连续梁无缝线路技术指标对比
4 多座铁路桥梁无缝线路设计对比分析
为进一步研究《新规》中的极限状态设计法对无缝线路设计结果的影响,分别从福平、宁安、郑万、商合杭、合福等多个铁路选取典型工点,分别采用极限状态法和容许应力法进行无缝线路结构检算。
4.1 计算工况
将本文选取的多个铁路项目桥上无缝线路工点概况汇总,列于表2中,计算工况覆盖了不同铁路等级、不同设计速度、不同轨道结构型式、不同桥梁跨度。
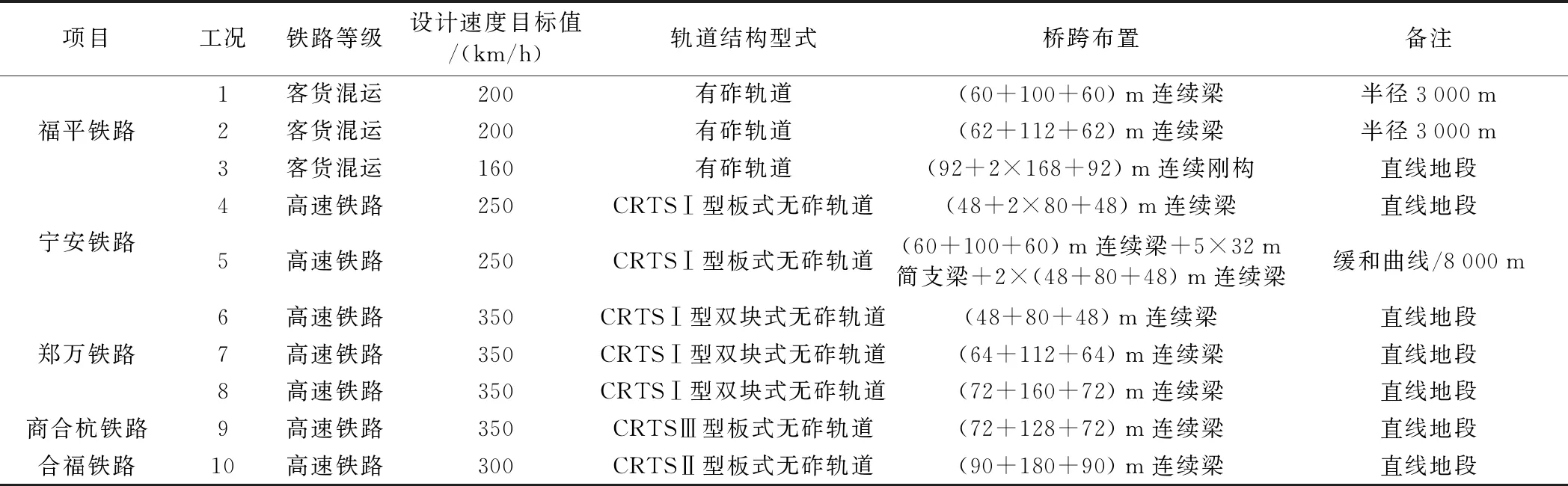
表2 多个铁路项目桥上无缝线路工点信息
4.2 无缝线路检算主要技术指标对比
分别采用《新规》的极限状态法和《现规》的容许应力法,对所选工况的无缝线路进行试设计。限于篇幅,本文直接列出所有工况采用极限状态法和容许应力法两种方法的检算结果,如表3所示。
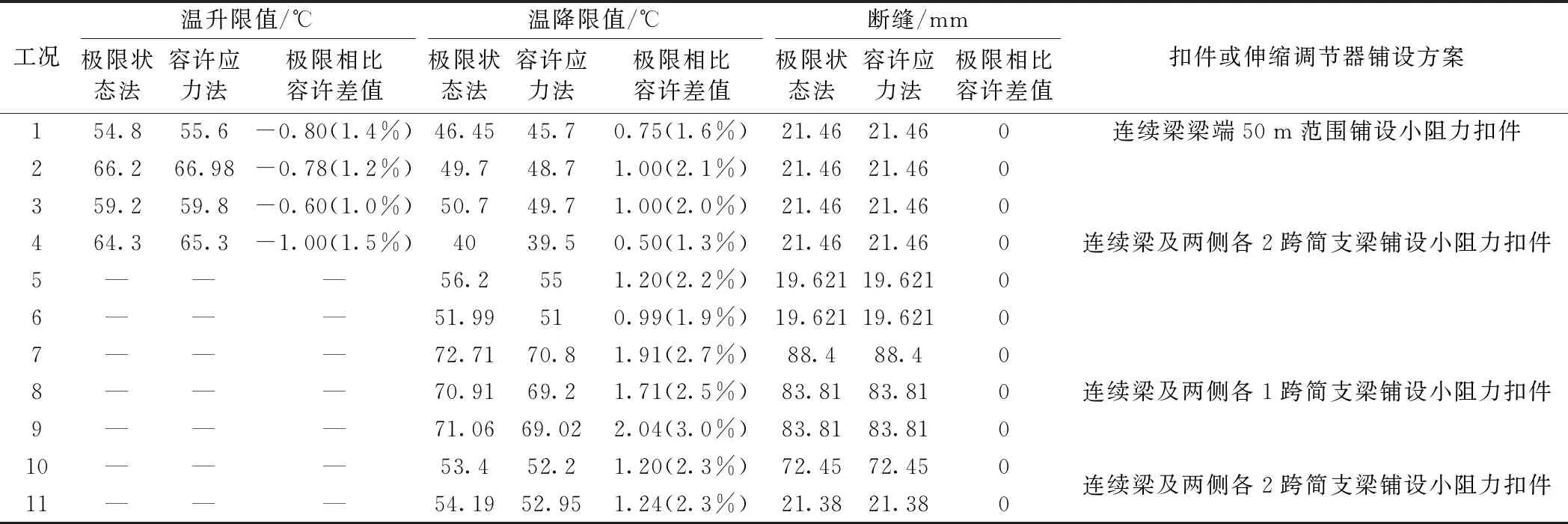
表3 桥上无缝线路极限状态法和容许应力法设计结果对比
将上述工况下,采用《新规》中的极限状态法和《现规》中的容许应力法得到的无缝线路检算结果绘制对比图,如图5、图6所示。从本文选取的工况的计算结果可以发现:
(1)极限状态法计算的最大温降普遍比容许应力法的温降限值大,最多增加2.0 ℃,增加幅度最大为3.0%;
(2)极限状态法计算的最大温升普遍比容许应力法的温升限值小,最多减小1 ℃,减小幅度最大为1.5%;
(3)极限状态法和容许应力法的断缝检算无差别。
根据以上各工点的计算结果,由于采用两种方法计算后均未引起扣件或伸缩调节器的铺设方案变化,从轨道工程的造价比较,两者的经济指标几乎相同,没有变化。

图5 两种方法的温升限值对比

图6 两种方法的温降限值对比
5 结论
从多个铁路项目中选取桥上无缝线路设计工点,分别采用《新规》的极限状态法和《现规》的容许应力法进行无缝线路设计计算,对比两种设计方法检算结果的主要技术指标。得出以下结论。
(1)对所选工况而言:极限状态法计算的最大温降普遍比容许应力法的温降限值大,最多增加2.0℃,增加幅度最大为3.0%;而极限状态法计算的最大温升普遍比容许应力法的温升限值小,最多减小1℃,减小幅度最大为1.5%;两种方法的断缝检算无差别。
(2)对所选工况而言:采用两种方法计算后均未引起扣件或伸缩调节器的铺设方案变化,从轨道工程的造价来说,两者的经济指标相同。
(3)采用《新规》极限状态法与《现规》容许应力法两种方法的无缝线路检算结果不完全一致,特殊工况下建议采用极限状态法进行无缝线路设计时,同时采用容许应力法进行校核。
(4)研究成果可为铁路无缝线路极限状态法设计研究和推广应用提供参考。

