抓住基本结构 任他千变万化

舒芳

同学们，有一类基本图形：三角形的两条内角平分线交于一点，两条外角平分线交于一点，或者一条内角平分线与一条外角平分线交于一点。围绕这类图的题灵活多变，角平分线还可以变为三等分线或者n等分线。但我们只要抓住基本原理，下次遇到也不用怕！

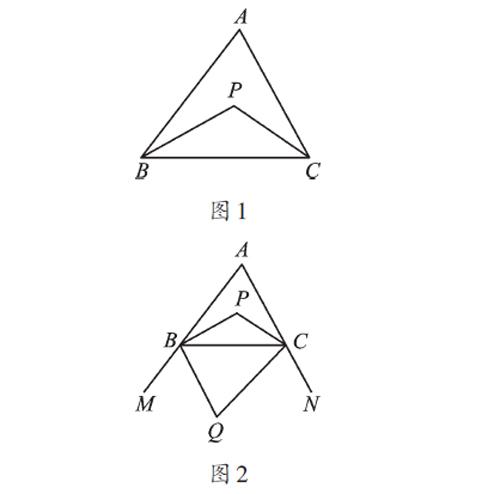
例题 如圖1，在△ABC中，∠ABC与∠ACB的平分线相交于点P。

（1）如果∠A=80°，求∠BPC的度数;

（2）如图2，作△ABC外角∠MBC、∠NCB的角平分线交于点Q，试探索∠Q与∠A之间的数量关系;

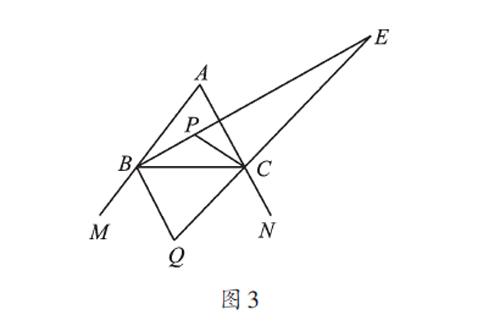
（3）如图3，延长线段BP、QC交于点E，试探索∠E与∠A之间的数量关系。

【错误】部分同学解答第（2）问时直接使用（1）中的条件“∠A=80°”，求出∠Q与∠A的具体度数，关系也没有总结出来。

【错因】审题不清，第（2）问惯性使用（1）中的条件;没有具体的数据，就不会抽象分析，没有真正领会“用字母表示数”的意义。

【解析】实际上，第（1）问可以把 “∠A=80°” 这个条件去掉，考虑一般的情况。“用字母表示数”，把∠A设为α°，运用三角形内角和定理表示∠ABC与∠ACB 的和，再用角平分线的定义，求出∠PBC+∠PCB，进而求出∠BPC，获得结论：∠BPC=90°[+12]∠A。

第（2）问类似上面的思路，根据三角形的外角性质分别表示出∠MBC与∠BCN的和为360°-∠ABC-∠ACB，即180°+∠A，再根据角平分线的定义可求得∠CBQ+∠BCQ，最后根据三角形内角和定理即可求得∠BQC=90°[-12]∠A。当然，在（1）知道∠BPC=90°[+12]∠A的基础上，我们还可以采用另一种方法。因为BP、BQ分别平分∠ABC、∠MBC，易证∠PBQ=90°，同理，∠PCQ=90°，最后利用四边形BPCQ的内角和为360°，可证得∠BQC与∠BPC是互补的，问题也可解决。

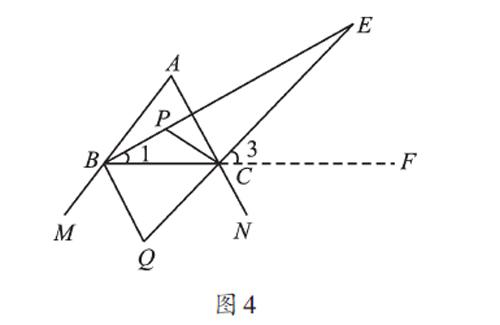
第（3）问中，∠E是由三角形的一条内角平分线与一条外角平分线相交得来的。可以用三角形一个外角等于与它不相邻的两个内角和来解决。如图4，延长BC至点F，∠3是△BCE的外角，有∠E=∠3-∠1;∠ACF是△ABC的外角，有∠A=∠ACF-∠ABC;再根据角平分线的定义，∠3=[12]∠ACF，∠1=[12]∠ABC，可证得∠E=[12]∠A。当然，也可由∠EBQ=90°知∠E与∠Q互余，进而获得结论。

【总结】由三角形内角或外角平分线相交产生的角，其基本图形和基本结论，我们可以总结成如图5的基本结构。其中最为重要的是对基本原理的掌握。

∠BPC是由△ABC的两条内角平分线相交得来，则∠BPC=90°[+12]∠A;

∠BQC是由△ABC的两条外角平分线相交得来，则∠BQC=90°[-12]∠A;

∠E是由△ABC的一条内角平分线与一条外角平分线相交得来，则∠E=[12]∠A。

【迁移】如图6，∠MON=90°，在△ABO中，∠ABC=[1n]∠ABN，∠BAD=[1n]∠BAO，则∠D=°（用含n的代数式表示）。

【解析】不难发现，∠D是由△ABO的一个外角n等分线与一个内角n等分线相交得来，我们可以将图5的基本原理迁移使用。因为∠ABN是△ABO的外角，有∠O=∠ABN-∠BAO;因为∠ABC是△ABD的外角，所以有∠D=∠ABC-∠BAD=[1n]∠ABN[-1n]∠BAO=[1n]（∠ABN-∠BAO）=[1n]∠O=[90°n]。

（作者单位：江苏省无锡市西漳中学）