从特殊到一般的学习方法
段刘宇


在“平面图形的认识(二)”中,我们用从特殊到一般的方法,依据“三角形的内角和是180°”得出多边形内角和的一般结论:180°?(n-2)(其中n为多边形的边数)。教材上是从四边形开始,通过添加辅助线,把四边形分成2个三角形,把五边形分成3个三角形,把六边形分成4个三角形……然后一般化,把n边形分成(n-2)个三角形,最终获得结论(当然分割转化的方法不唯一)。
教材上研究的都是凸多边形。凸多边形指如果把多边形的任意一条边向两方无限延长成为一直线时,其他各边都在此直线的同一旁的多边形。凸多边形的内角没有一个是优角(大于180°且小于360°的角),如图1。凹多边形指把一个多边形的某条边向两方无限延长成为一直线时,其他各边不全在此直线的同一旁的多边形。凹多边形的内角中至少有一个优角,如图2。凹多边形的内角和也是一样的结论吗?
我们可以先回顾一下探究凸多边形内角和的方法,然后将同样的办法迁移到探究凹多边形的内角和中。
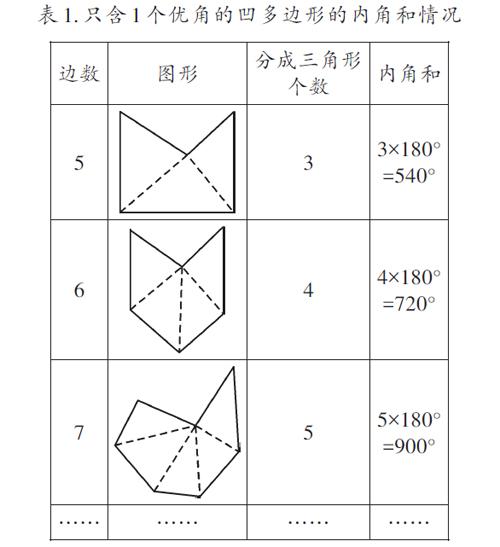
以凹四边形为例,如图3。连接点A和点C,线段AC把这个凹四边形分为两个三角形,这两个三角形的内角和就是这个凹四边形的内角和,即2×180°=360°。看到这个结果,我们不由自主地猜想:凹多边形的内角和公式会不会跟凸多边形的内角和公式一样呢?多举几个例子,如表1。
这样,我们就更有理由归纳一般性规律,即凹n边形内角和为180°?(n-2)(其中n为多边形的边数),这与凸n边形的结论一样。
但这仍然是片面的,如果凹多边形包含两个及以上优角,该结论还能不能成立呢?不妨以包含两个优角的凹多边形为例,如表2。
我们仍然可以类似地去考虑含3个优角(从凹八边形开始)的凹多边形,特殊的例子越充分、越全面,我们就越有信心确信凹n边形内角和的结论。
因此,不论是凸多形还是凹多邊形,可以得到一个关于多边形内角和的通用公式,即n边形的内角和为180°?(n-2)(其中n为多边形的边数)。
这是一个多么简洁美妙的结论啊!小伙伴们,从特殊到一般,这是我们在看教材、学新知的时候,经常碰到的方法。特殊的例子中蕴含着一般的规律,一般的规律可以用特殊的例子验证。当我们运用这种方法迁移运用、研究问题的时候,就能体验到发现的乐趣,体会到结论的美妙,领悟到方法的神奇。同学们,在遇到具有一般性的问题时,试着用特殊到一般的方法大胆探索吧。
教师点评
学习数学不仅仅是记住结论,更应该掌握数学结论形成的过程及其蕴含的数学思想方法,更包含在过程中所感受到的积极情感、数学之美和严谨求证的价值观念等。小作者不仅能够学好多边形内角和的结论,还能够把结论形成过程中的方法迁移到更全面的多边形的不同类别中,最终形成了更全面的认识。在这个过程中,他不仅学会了知识,更掌握了方法,还领悟了特殊与一般的关系,获得了美好的体验,产生了对数学学习的积极的兴趣。他的这种学习方法,值得同学们借鉴。
(指导教师:钟 鸣)

