利用自发拉曼散射建立三个原子节点的纠缠*
刘艳红 周瑶瑶 闫智辉 贾晓军
1) (太原师范学院物理系, 晋中 030619)
2) (太原师范学院, 计算物理与应用物理研究所, 晋中 030619)
3) (山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原 030006)
4) (山西大学, 极端光学协同创新中心, 太原 030006)
量子纠缠是一种关键的量子资源.随着量子信息技术的发展, 由量子通道和量子节点组成的量子网络成为研究的热点.量子信息网络的建立需要在多个远距离的量子节点间建立纠缠, 它在分步式量子计算及量子因特网等方面有很重要的应用价值.本文在光和原子混合纠缠的基础上, 提出了结合前馈网络建立三个独立的远程原子系综之间的连续变量确定性纠缠.三个原子系综分别放置在三个远程的节点中, 每个节点首先通过自发拉曼散射过程制备光和原子的混合纠缠; 然后, 利用平衡零拍探测器测量三束Stokes 光场干涉后的量子噪声, 并将测量的结果前馈到原子系综, 在三个独立的远距离的原子系综间建立纠缠; 最后, 利用来自三个原子系综的三束反斯托克斯光束的关联方差通过三组份不可分判据验证三个原子系综的纠缠.该方案简单可行,可以拓展到基于不同物理系统的量子节点, 甚至实现更多原子节点的纠缠, 从而实现大规模量子信息网络.
1 引 言
量子纠缠是实现量子通信和构建量子信息网络的一种关键的量子资源[1,2].伴随着量子信息科学的快速发展, 由量子节点和连接量子节点的量子通道构成的量子网络开辟了广阔的科学领域[3].光是最好的量子信息载体, 可以用来传输量子态和连接量子节点.原子系综[4−10]、单原子[11,12]、囚禁离子[13−15]、光力系统[16−20]、超导体[21−23]、固态系统[24−27]和其他物理系统都可以被用作量子节点.量子信息网络的发展需要在量子节点间产生、存储及分发纠缠的能力.近年来, 两个量子节点间的纠缠已经实现[28−38].伴随着量子信息网络的发展, 利用量子存储已经实现了三个和四个原子系综的预告式纠缠[39,40].产生、存储和释放三个原子系综的确定性纠缠已经实现[41].多个量子节点间高纠缠度的远距离的确定性量子纠缠的建立是未来量子信息网络和量子力学进一步发展的显著目标.
量子态转移是建立量子节点间纠缠的一种有效的方法, 其中前提是必须制备多组份的纠缠态光场[28−33,41].多组份纠缠态光场的建立多用参量下转换的方法[42,43], 并且已经广泛应用于各种量子方案中.基于电磁感应透明相互作用可以将纠缠态的量子信息映射到原子自旋波, 因此原子自旋波的纠缠可以被产生并存储.在原子的相干时间内, 纠缠态可以从原子自旋波释放到光场, 进而可以验证原子系综的纠缠, 并且可以用于其下游应用.另一方面, 光和原子的混合纠缠结合光子间的干涉可以运用在多个原子系综预告式纠缠的产生[39,40], 与原子系综纠缠的光场可以在量子信道中传输, 以连接和纠缠不同的遥远的原子系综.
本文在光和原子混合纠缠的基础上, 提出了结合前馈网络来产生三个空间分离原子系综的连续变量确定性纠缠.由于光与原子系综相互作用集体增强, 原子系综适合作为量子节点.在我们的方案中, 只需要三个原子系综, 以及由干涉、测量和射频线圈组成的前馈网络就可以将三个原子系综纠缠在一起.该方案的实现不需要制备纠缠态光场,使整个实验系统简单稳定.首先, 通过自发拉曼散射过程, 在写光的作用下三个原子系综产生三束Stokes 光场; 然后, 第一和第二束Stokes 光场在第一个分束比为R1∶T1光学分束片(BS1)上干涉, 并且来自于BS1 的其中一束输出场和第三束Stokes 光场在第二个分束比为R2∶T2光学分束片(BS2)上耦合.用平衡零拍探测器分别测量三束Stokes 光场干涉后输出光场的正交振幅和正交相位的量子噪声.最后, 通过射频线圈将测量的正交振幅和相位的结果前馈给三个原子系综.在用户控制的时间内, 将存储的三个原子系综的纠缠态释放到三束反斯托克斯光场中, 用于验证三个原子系综的纠缠及其在量子网络中的应用.
2 三个原子系综确定性纠缠的产生
三个远距离原子系综确定性纠缠的产生原理图如图1 所示.这个系统包括三个独立的原子系综A, B 和C, 两个光学分束片BS1 和BS2, 三套平衡零拍探测器BHD1, BHD2 和BHD3.三个原子系综A, B 和C 分别放置在三个射频线圈中间,平衡零拍探测器由一个50/50 的分束片、一对光电二极管和一个功率减法器组成.三束斯托克斯光束由自发拉曼散射过程产生分别来自于原子系综A, B 和C,在分束比为R1∶T1的光学分束片BS1 上干涉产生两束光, 其中一束干涉后的输出光与在分束比为R2∶T2的光学分束片BS2 上干涉, 分别产生三束光,用平衡零拍探测器BHD1, BHD2 和BHD3 分别测量的正交振幅、相位和振幅分量的噪声.将BHD1, BHD2 和BHD3 探测到的信号通过射频线圈分别前馈到原子系综A, B 和C, 最终建立三个远程原子系综A, B 和C 之间的纠缠.
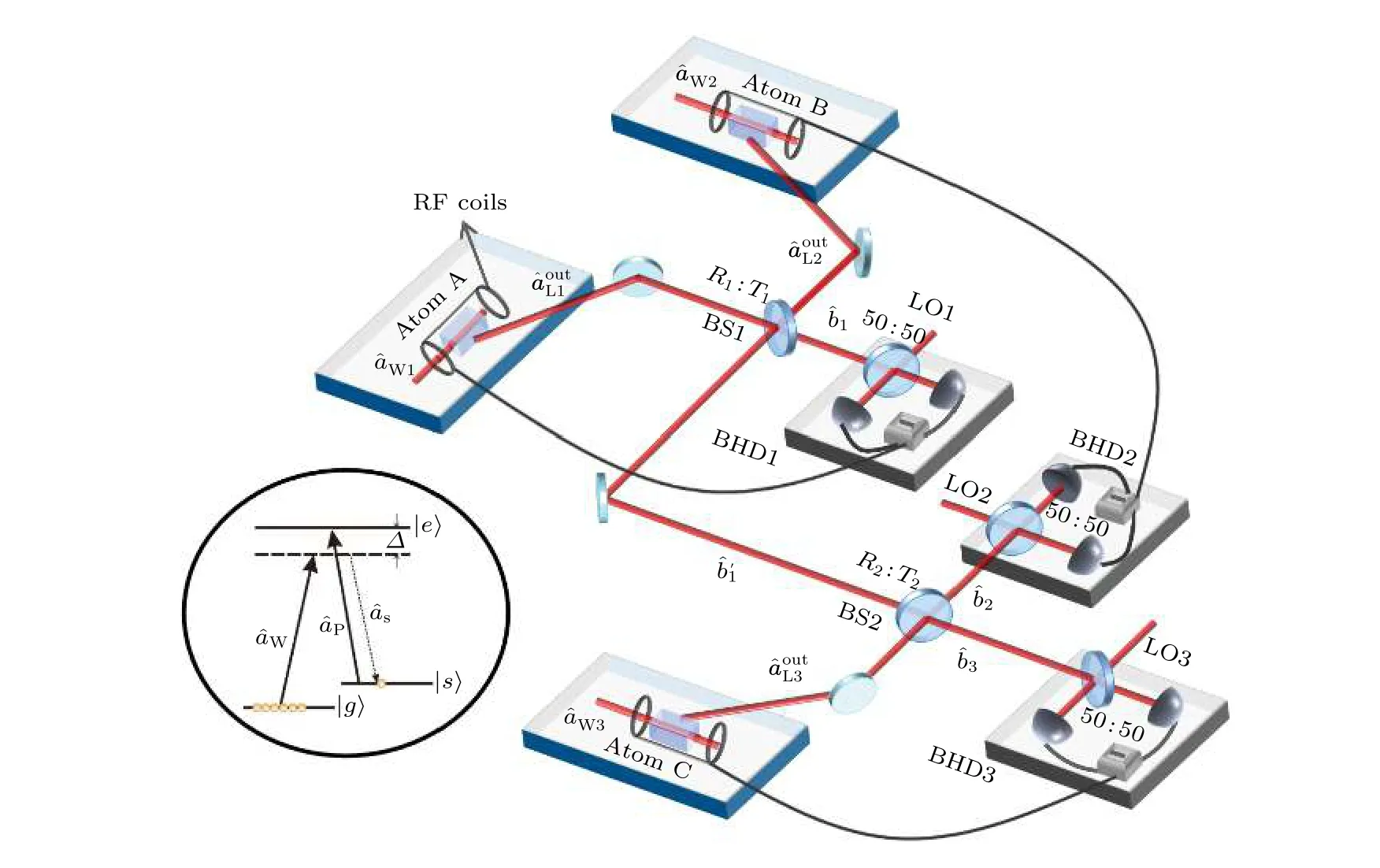
图1 三个原子系综确定性纠缠产生原理图Fig.1.Schematic diagram of deterministic entanglement generation among three atomic ensembles.
2.1 光和原子系综纠缠的产生
在量子光学理论中, 光场由产生和湮灭算符和来表示.光场的正交振幅分量和正交相位分量分别对应湮灭算符的实部和虚部,,.原子总的自旋波Sˆ 可以用庞加莱球上的Stokes 矢量描述, 且可以被看作满足玻色对易关系同样, 原子自旋波的振幅和相位分量分别对应的实部和虚部,=当原子自旋波通过自发拉曼散射过程和信号光、抽运光耦合时, 光和原子系综的纠缠建立.制备纠缠的原子系综的能级结构如图1 左下角插图所示, 该原子具有 Λ 型能级结构, 存在基态|g〉、亚稳态|s〉和激发态|e〉.起初, 原子通过光学抽运光制备在基态, 在写脉冲的作用下, Stokes 光场和总的原子自旋波同时产生.在相互作用表象下, 该系统的有效相互作用哈密顿量可以写为如下形式:
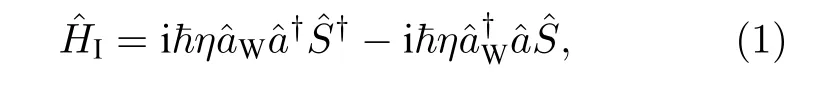
式中,η是光和原子的相互作用常数,η=其中κeg和κes是光和原子的耦合系数,Na是总的原子数,Δ是写光和Stokes 光场的失谐.在这里假设所有的失谐均相等且忽略损耗.
当一束强的写脉冲光作用于原子系综时, 自发拉曼散射过程发生, 并且其哈密顿量类似于参量下转换模型
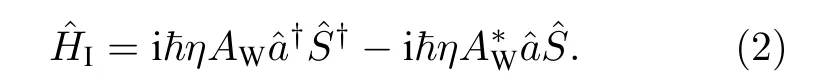
其中AW是强的写光脉冲的归一化振幅,是其共轭.
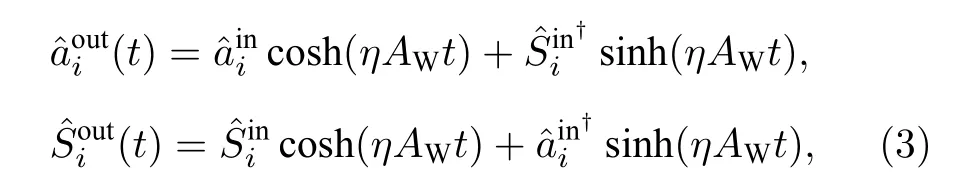
其中i=1,2,3 分别对应在原子系综A, B 和C 中.根据算符线性化表达式, 算符可以表示为平均值和波动的和, 即.输入光场可以看作真空光场, 其量子波动根据段路明等[44]和Simon[45]提出的光场的两组份不可分判据, 可以将其拓展到光和原子.如果光和原子系综的正交分量的关联方差和小于4, 那么光和原子间存在纠缠.光和原子的关联方差V等于
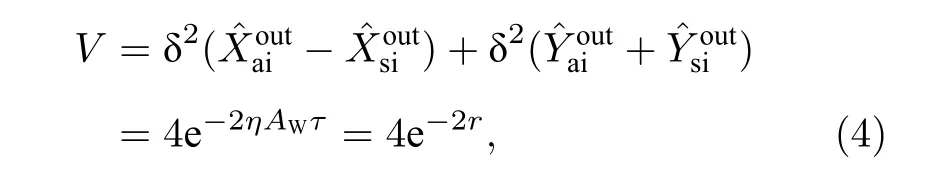
其中τ是光和原子的相互作用时间.很明显光和原子相互作用的关联度依赖于关联参量r=ηAWτ=r越大, 关联方差越小.当r= 0时,V= 4 对应相干态的关联方差, 它被定义为量子噪声极限(quantum noise limit, QNL); 当r> 0时, 光和原子的关联方差V小于QNL, 这意味着光和原子间存在纠缠; 当r→∞,V→ 0 此时获得的纠缠为完美纠缠.
2.2 通过前馈网络建立三个原子系综的纠缠
接下来, 考虑如何实现三个原子系综A, B 和C的纠缠.原子系综A 和B 通过自发拉曼散射过程产生的Stokes 光场和在分束比为R1∶T1的光学分束片BS1 上干涉, 干涉后的其中一束输出光与产生于原子系综C 的Stokes 光束在分束比为R2∶T2的光学分束片BS2 上干涉, 输出的三束光场可以写为
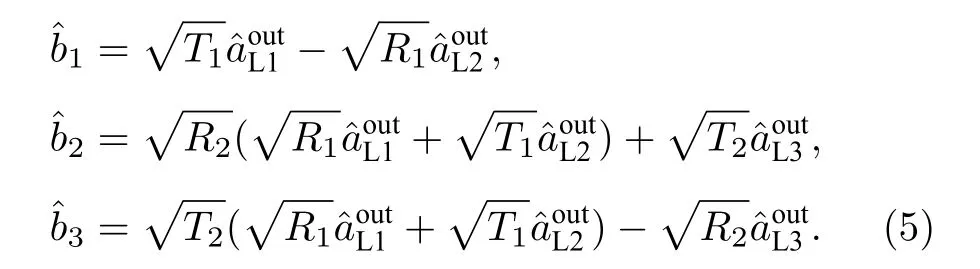
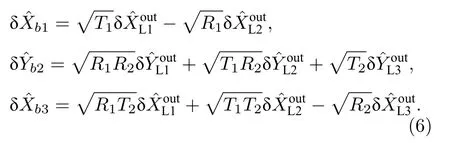
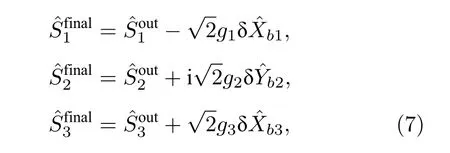
三个原子系综纠缠的实现通过三组份不可分判据来验证:
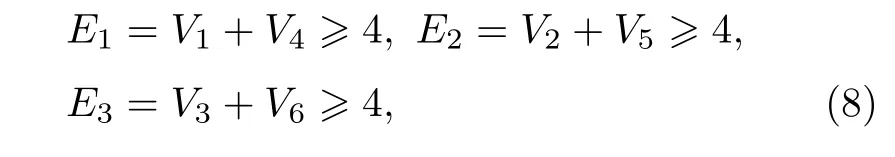
其中Vi(i=1,2,··· ,6) 代表不同正交分量的关联方差,上述不等式中右边的4 代表三组份纠缠不可分的边界.当E1,E2和E3中任意两个关联方差之和小于量子噪声极限时, 三个原子系综是三组份类Greenberger-Horne-Zeilinger (GHZ)纠缠态.g4,g5和g6是可调节的经典测量增益因子为了获得原子系综的最小关联方差之和.系统中不可避免的传输损耗会影响原子系综纠缠的质量.除此之外, 纠缠交换的质量被原子的相干寿命限制,这段时间保证了原子系综的纠缠, 因此原子的相干寿命影响原子系综的纠缠.在热原子系综中相干寿命高于5 ms[46], 甚至可以达到40 ms[37], 在冷原子系综中相干寿命可以达到秒级[47], 这个时间足以维持测量和纠缠交换的时间, 因此足够建立三个原子系综的纠缠.为了证明三个原子系综的纠缠, 分别用三束读光脉冲同时作用于原子系综A, B 和C, 通过自发拉曼散射过程将原子系综的量子态转换到反斯托克斯光场的量子态.三束反斯托克斯光场的正交分量的关联方差可以用来验证三个远距离原子系综间的纠缠.
3 三个原子系综纠缠的验证
图2 和图3 给出了原子系综的最终关联方差之和E1,E2,E3的变化曲线.分别计算E1,E2,E3的最小值, 可以得到最佳测量增益因子的表达式, 最佳测量增益因子依赖于前馈增益因子g2、压缩参量r及光学分束片BS1, BS2 的反射率R1,R2.经过理论计算后原子系综的关联方差之和E1与前馈增益因子g1,g2有关,E2与前馈增益因子g1,g2,g3有关,E3与前馈增益因子g2,g3有关, 且E1,E2,E3都依赖于压缩参量r及光学分束片BS1, BS2 的反射率R1,R2.由于存在前馈网络的影响, 原子系综关联方差之和E1,E2,E3的变化曲线比较复杂, 随后分别分析各参量对原子系综关联方差之和E1,E2和E3的影响.
图2 描述了原子系综的关联方差之和E1,E2,E3与光学分束片BS1, BS2 反射率R1,R2的依赖关系, 图2(a)和图2(b)对应E1的变化曲线, 图2(c)和图2(d)对应E2的变化曲线, 图2(e)和图2(f)对应E3的变化曲线.图2 中, 曲线1 代表QNL,曲线2, 3, 4, 5, 6, 7 表示光学分束片BS1 的反射率R1分别取0.1, 0.2, 0.3, 0.5, 0.7 和0.9 时, 原子系综关联方差之和随光学分束片BS2 的反射率R2的变化曲线.在我们的方案中, 压缩参量的取值r= 0.8, 前馈增益因子的取值分别为g1=0.8 ,g2=1.0 ,g3=0.8 , 所有的参量值在实验上均可以达到, 为实验系统的设计提供了理论参考.从图2(a)和图2(b)可看到: 在R1取值一定时, 原子系综的关联方差之和E1随着R2的增大而减小; 在R2一定时,E1随着R1的增大先减小后增大, 在R1= 0.5时关联方差之和E1的值最小.从图2(a)和图2(b)得到在R1= 0.5,R2在小于1 的范围内取值越大时, 原子系综关联方差之和E1的值越小.在图2(d)中, 当光学分束片BS1 的反射率R1= 0.9 时, 不存在R2的取值使得关联方差之和E2小于量子噪声极限.对比图2(c)和图2(d), 从曲线4 看出R1=0.3,R2取值在0.7 附近时,E2可以达到最小值.从图2(e)和图2(f)发现: 在R1= 0.9 时, 不存在使E3小于量子噪声极限的R2的值, 并且在R2一定时,R1越大E3的值越大; 当R1取定值时,R2存在最佳值使得关联方差之和E3的值最小.对比图2(e)和图2(f)得到, 在R1取值越小,R2= 0.6 时,E3的值最小.
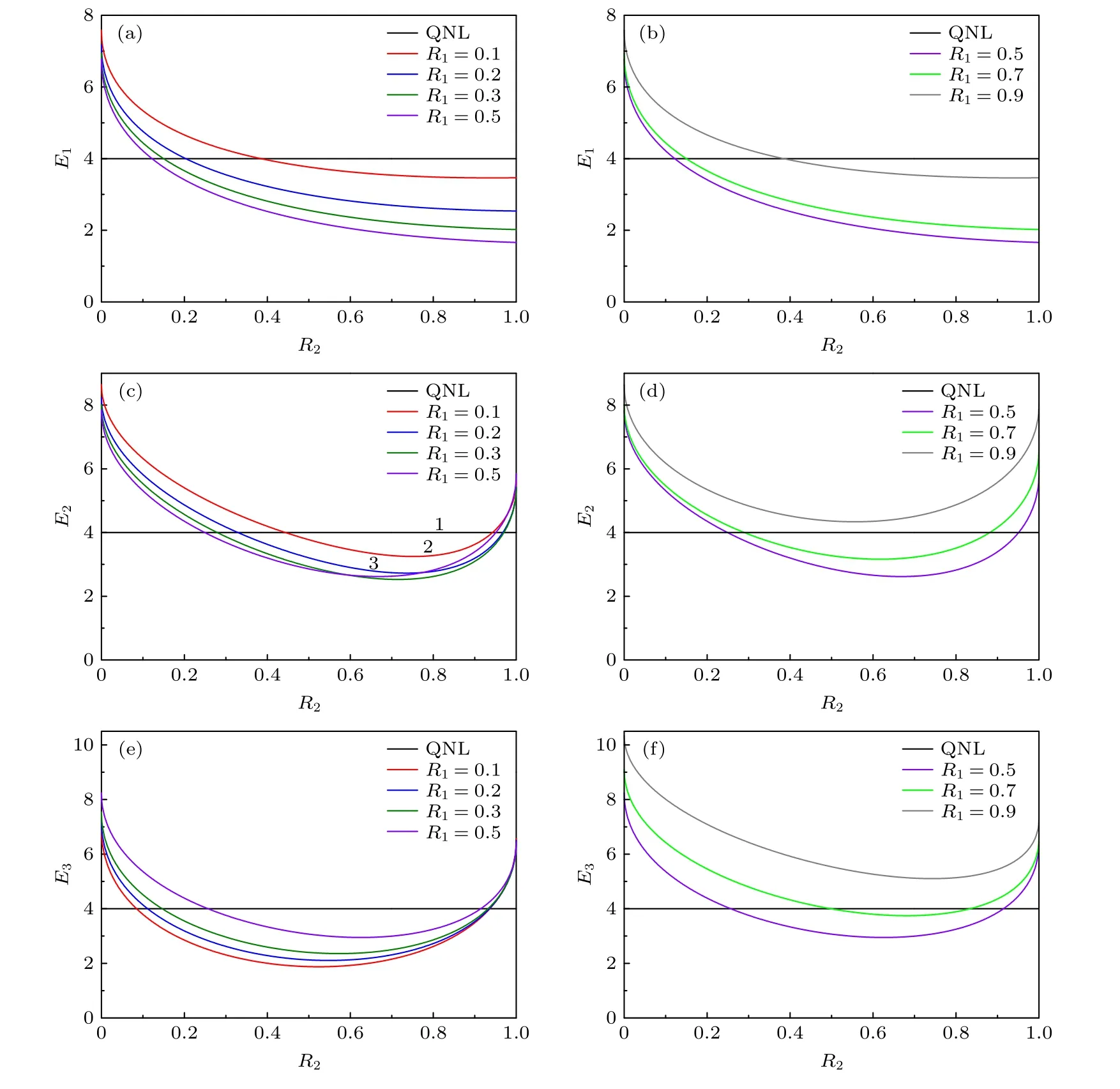
图2 原子系综关联方差之和E1, E2, E3 随光学分束片BS2 的反射率R2 的变化曲线 (a), (c), (e) BS1 的反射率R1 =0.1, 0.2,0.3, 0.5 ; (b), (d), (f) BS1 的反射率R1 =0.5,0.7,0.9Fig.2.Dependence of the correlation variance combinations of atomic ensembles E1, E2, E3 on the reflectivity R2 of the second optical beam splitter BS2: (a), (c), (e) Reflectivity R 1 =0.1, 0.2, 0.3, 0.5 of BS1; (b), (d), (f) reflectivity R 1 =0.5,0.7,0.9 of BS1.
当关联方差之和E1,E2,E3越小时, 原子系综间的纠缠度越大.图2 中, 综合考虑原子系综的不同三个关联方差之和E1,E2,E3, 为了满足原子系综的关联方差之和E1,E2,E3同时小于量子噪声极限4, 取光学分束片BS1 和BS2 的反射率R1,R2分别是0.3, 0.6.当压缩参量r= 0.8, 前馈增益因子g1,g2,g3分别取0.8, 1.0, 0.8, 分束片的反射率R1,R2的取值分别为0.3, 0.6 时,E1,E2,E3分别等于2.36, 2.65, 2.36, 此时三个关联方差之和均小于量子噪声极限, 三个原子系综处于不可分状态.
当分束片BS1, BS2 的反射率分别取0.3, 0.6,测量增益因子g4,g5,g6取最佳值时, 关联方差之和E1,E2,E3受前馈增益因子g1,g2,g3的影响不同.理论计算E1,E2,E3的最小值所得g1,g2,g3最佳取值不同, 因此不能同时取g1,g2,g3的最佳值使得关联方差之和E1,E2,E3最小.图3 描述了原子系综的关联方差之和E1,E2,E3与前馈增益因子的g1,g2,g3的依赖关系.
图3(a)表示E1与前馈增益因子g1,g2的曲线图, 图3(b)表示E3与前馈增益因子g2,g3的曲线图, 图3(c)表示E2与前馈增益因子g1,g2的曲线图.图3(a)中, 曲线1 表示QNL, 曲线2, 3, 4,5 表示前馈增益因子g1分别取0.7, 0.8, 0.9, 1.0 时,原子系综关联方差之和E1随前馈增益因子g2的变化曲线.当g1取定值时, 存在最佳前馈增益因子g2使得E1最小.观察图3(a), 发现g1=0.9 ,g2=1.0时, 原子系综的关联方差之和E1达到最小值, 且最小值为2.31.图3(b)中, 曲线1 代表QNL, 曲线2, 3, 4, 5 代表前馈增益因子g3分别取0.7, 0.8,0.9 和1.0 时, 原子系综关联方差之和E3随前馈增益因子g2的变化曲线.从图3(b)得到: 当g3=0.7或g3=1.0 时, 曲线2, 5 几乎重合; 当g3=0.8 或g3=0.9 时, 曲线3, 4 重合.当g3=0.8 或g3=0.9 ,g2=1.0时, 原子系综关联方差之和E3可取最小值2.36.图3(c)表示g3=0.8 和g3=0.9 时E2与前馈增益因子g1,g2的曲线图.图3(c)中, 曲线1 表示QNL, 曲线2, 3, 4, 5 代表前馈增益因子g1分别取0.7, 0.8, 0.9, 1.0 时, 原子系综关联方差之和E2随前馈增益因子g2的变化曲线, 实线和虚线分别表示g3取0.8, 0.9.从图3(c)发现:g2一定时, 随着g1的增大, 原子系综的关联方差和E2也在增大,且g3取0.8 时E2的值大于g3取0.9 时E2的值; 当g1取定值时,g2存在最佳值使得E2最小.综合上述分析, 由于不能同时取g1,g2,g3的最佳值使得E1,E2,E3最小.当g1=0.8 ,g2=1.0 ,g3=0.8 时,E1,E2,E3分别等于2.36, 2.65, 2.36.
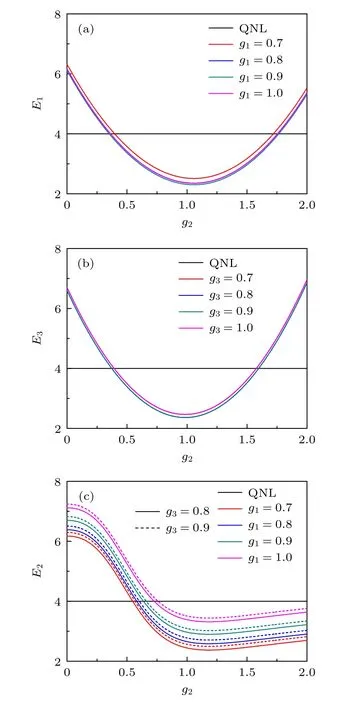
图3 原子系综关联方差之和E1, E2, E3 与前馈增益因子g2 的变化曲线 (a) g 1 =0.7, 0.8, 0.9, 1.0 时, E1 的变化曲线; (b) g 3 =0.7, 0.8, 0.9, 1.0 时, E3 曲线; (c)g1 =0.7,0.8, 0.9, 1.0时, E2 的变化Fig.3.Correlation variance combinations E1, E2 and E3 versus the feedforward gain factor g2 : (a) The correlation variance combination E1 versus g2 wheng1 =0.7,0.8, 0.9, 1.0; (b) the correlation variance combinations E3 versus g2 when g 3 =0.7, 0.8, 0.9, 1.0 ; (c) the correlation variance combinations E2 versus g2 wheng1 =0.7, 0.8,0.9, 1.0.
当分束片BS1, BS2 的反射率分别为R1= 0.3,R2= 0.6, 前馈增益因子g1= 0.8,g2= 1.0,g3=0.8, 测量增益因子时,关联方差之和E1,E2,E3同时小于4, 此时三个原子系综是类GHZ 纠缠态.
4 总 结
我们提出了一种通过干涉和前馈网络来确定纠缠三个空间分离原子系综的方案.首先, 利用自发拉曼散射过程分别在三个原子系综中制备光场和原子自旋波之间的纠缠态, 并利用光场连接和纠缠远程的量子节点.三束Stokes 光场在不同比例的分束片网络上干涉, 用平衡零拍探测探测器测量干涉后光场的量子噪声.最后根据测量结果, 通过经典的前馈, 得到了三个原子系综的纠缠.通过优化前馈网络可以得到三个原子系综的最佳纠缠.将光和原子的混合纠缠结合前馈网络可以纠缠更多的原子节点.此外, 我们的方案还可以推广到其他量子节点候选者, 如囚禁离子、超导体等.如果将纠缠蒸馏与我们的方案相结合, 量子节点间的距离可以明显增加[48].这一简单可行的方案为简化大规模量子互联网提供了途径, 弥补了原理上与现实世界量子信息科学应用之间的差距.