不同坡度下扭王字块体护面斜坡堤越浪量的试验研究

孙大鹏，孙文豪，王 红，修富义，刘 飞

(1.大连理工大学 海岸和近海工程国家重点实验室，大连 116024；2.南京水利科学研究院，南京 210029；3.亿达中国控股有限公司，大连 116024；4.长春中海地产有限公司，长春 130000)

在斜坡堤上越浪量的物理模型试验研究，众多学者已经取得了许多成果。Van der Meer[1]基于大量的物模试验，给出了平均越浪量的关系式，其中包含了平均坡度、平台宽度、坡面糙率系数以及波向等因素；俞聿修[2]研究了斜坡堤堤坡、堤顶超高及波谱宽度与越浪量之间的关系，并总结了入射波为不规则波时，光滑不透水单坡堤无因次越浪量的关系式；李晓亮[3]以三维物理模型试验为基础，通过分析当斜向和多向波作用在斜坡堤上时，波参数及斜坡堤结构参数对越浪量的影响，得出了斜坡堤越浪量的估算公式，该关系式适用于护面为混凝土的斜坡堤和扭工字块体斜坡堤；王红[4]和章家昌[5]提出了无胸墙斜坡堤和有胸墙斜坡堤越浪量的关系式，但公式适用的护面块体并不包含扭王字块；范红霞[6]结合波浪破碎参数、胸墙高度、墙顶超高及块体种类等拟合了斜坡坡度系数为2.0的斜坡堤越浪量计算方法；周雅[7]研究了波要素及断面尺度对斜坡堤越浪量的影响，并对规则、随机两种块体摆放型式的消浪效果进行了比较；孙大鹏[8]借助物理模型试验，结合了相对坡肩宽度、波陡、相对块体尺寸、相对胸墙高度、相对水深和相对堤顶超高等因素，提出了护面结构影响系数的关系式和越浪量的关系式，但其成果仅适用于坡度系数为1.5的情况。数值模拟方面，黄宁[9]、王键[10]基于FLUENT软件关于斜坡堤的越浪量都进行了有效的探索，并取得了较好的成果。

目前扭王字块斜坡堤越浪成果中各家公式仍然存在局限。《港口与航道水文规范》[11]中给出计算斜坡堤堤顶带胸墙平均越浪量的表达式如下

(1)

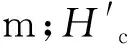
本文基于孙大鹏[8]的前期试验成果(m=1.5)，综合了诸多斜坡堤越浪量的影响因素，进行波浪水槽中的物模试验，通过非线性拟合给出入射波为不规则波时，扭王字块体斜坡堤护面结构影响系数的关系式和越浪量的关系式。

1 试验概况

1.1 试验模型及条件

试验在大连理工大学海岸和近海工程国家重点实验室进行，水槽底为平底，水槽长50 m、宽3 m、高1 m，模型布置在距离造波板30 m处，末端位置铺设消波网用于消波。入射波为不规则波，波谱采用平均JONSWAP谱，峰高因子γ=3.3，多数使用经验表明，此谱符合实测结果，应用广泛。

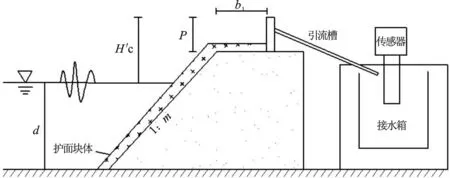
图1 物模试验断面图Fig.1 Section of physical experiment model

图2 扭王字块体几何尺寸图Fig.2 The geometry of accropode blocks

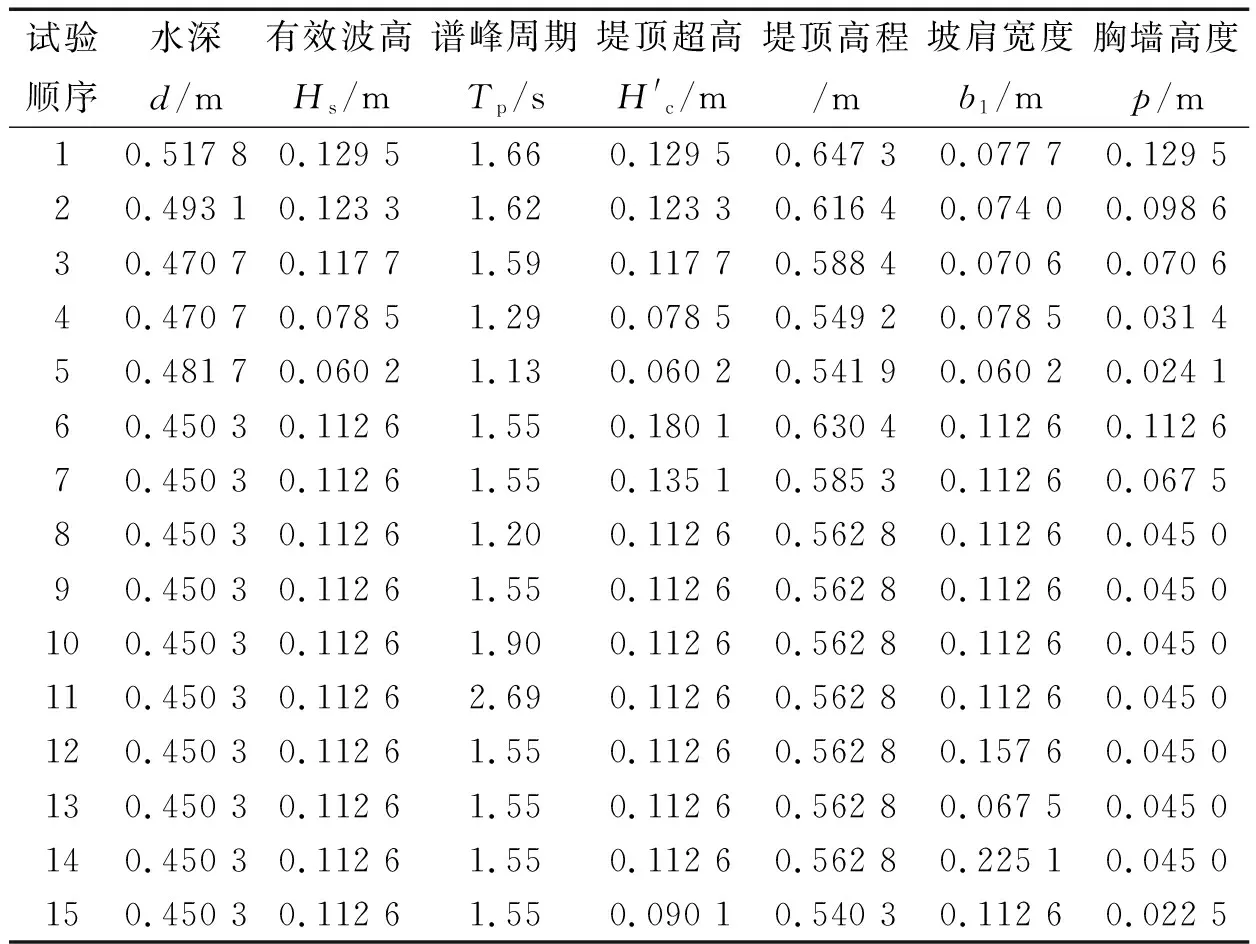
表1 试验工况Tab.1 The experimental conditions

进行光滑混凝土板斜坡堤的越浪试验后，再进行四种不同尺寸扭王字块斜坡堤的越浪试验。试验工况如表1，共计3×5×15组次，每组至少进行3次，保证结果有较好的重复性。

1.3 试验数据采集

试验及采样时应不少于100个波，因此，当Tp<2.0 s时，采样时间设为164 s；当Tp﹥2.0 s时，采样时间设为328 s。收集及测量越浪量的装置如图1。当波浪越过斜坡堤时，水体会通过引流槽流入接水箱中，接水箱固定在重量传感器上，传感器与电脑连接，电脑可以记录越浪量的变化过程，每次试验总的越浪量可以在电脑上读取。此测量装置经过试验验证，结果可靠。

2 光滑混凝土板斜坡堤越浪量的试验结果

规范[11]中，当斜坡堤的堤顶带有直立胸墙时，其越浪量是在光滑混凝土板越浪量的基础上进行计算。延续规范[11]的这一编制思路，综合坡度、相对坡肩宽度、波陡、相对胸墙高度、相对水深和相对堤顶超高等多种因素，先行研究光滑混凝土板斜坡堤的越浪量。基于孙大鹏[8]的前期成果，当4.0≤d/Hs≤8.0时，d/Hs对Q板/(gHs3)0.5基本没有影响；章家昌[5]亦曾给出当d/Hs≥3.93时，水深对越浪量几乎没有影响的试验结论。故在光滑混凝土板斜坡堤越浪量的分析中忽略相对水深这一因素。

基于π定理，给出混凝土板斜坡堤平均越浪量关系式如下

(2)

式中：Q板为光滑混凝土板斜坡堤的平均越浪量，m3/m·s；L为谱峰周期对应的波长，m；Hs为有效波高，m。

2.1 Q板/(gHs3)0.5与Hs/L之间的关系

依据单一变量法，其他因素不变时，不同Hs/L对应的Q板/(gHs3)0.5结果如图3，当Hs/L增大，Q板/(gHs3)0.5减小，表现为指数关系。

2.2 Q板/(gHs3)0.5与之间的关系

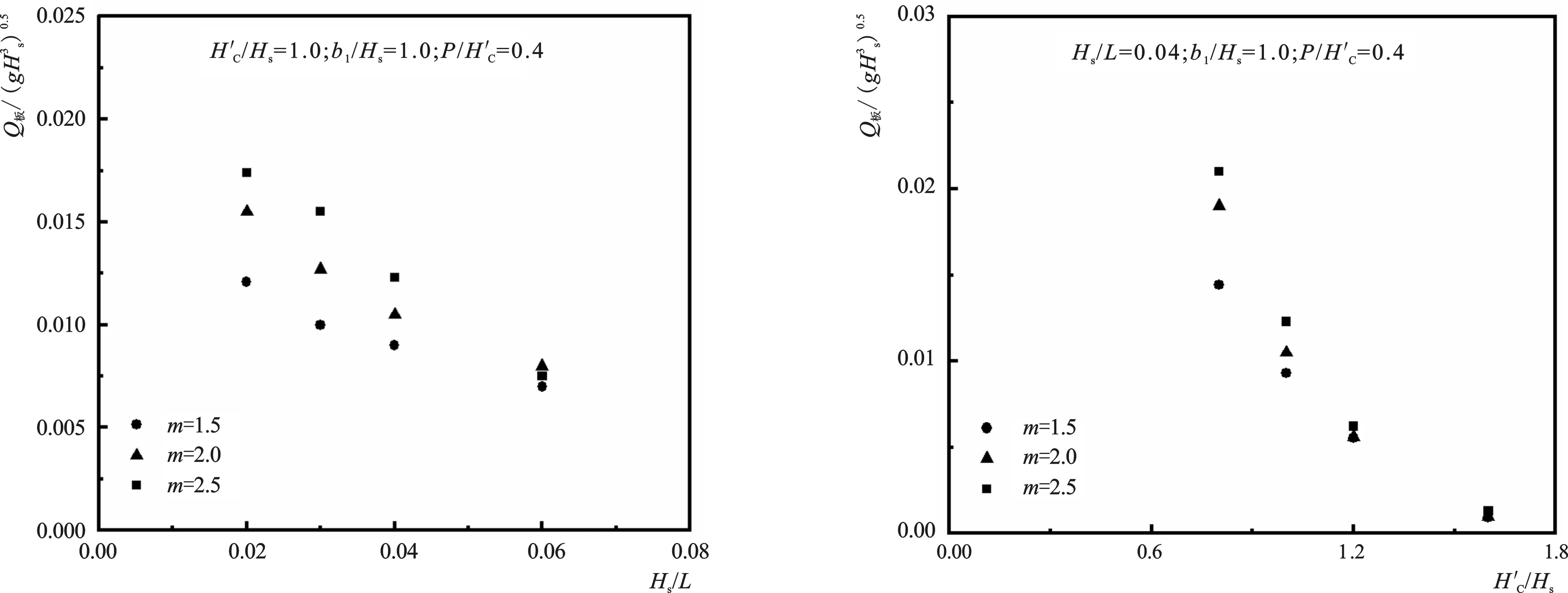
图3 Q板/(gHs3)0.5与Hs/L之间的关系Fig.3 Relationship between Q板/(gHs3)0.5 and Hs/L图4 Q板/(gHs3)0.5与H'c/Hs之间的关系Fig.4 Relationship between Q板/(gHs3)0.5 and H'c/Hs

2.3 Q板/(gHs3)0.5与b1/Hs之间的关系

依据单一变量法，其他因素不变，不同b1/Hs对应的Q板/(gHs3)0.5结果如图5，当b1/Hs增加时，Q板/(gHs3)0.5减小，表现为指数关系。

2.4 Q板/(gHs3)0.5与之间的关系

2.5 Q板/(gHs3)0.5与m之间的关系

依据单一变量法，其他因素不变，不同m对应的Q板/(gHs3)0.5结果如图7，当斜坡坡度系数m增大时，Q板/(gHs3)0.5也增加，表现为指数关系。

2.6 光滑混凝土板斜坡堤越浪量的计算关系式

(3)

规范[11]公式(1)和本文提出的公式(3)计算值与本文物理模型试验值的对比如图8。由图可知，规范[11]公式的计算值偏小；本文公式综合考虑了斜坡堤越浪量的诸多影响因素，可以看出本文公式的计算值更为接近试验值。本文公式(3)的相关系数R>0.98，相关性较好。在后文用本文公式计算光滑混凝土板斜坡堤的越浪量。

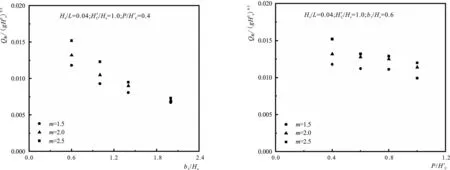
图5 Q板/(gHs3)0.5与b1/Hs之间的关系Fig.5 Relationship between Q板/(gHs3)0.5 and b1/Hs图6 Q板/(gHs3)0.5与P/H'c之间的关系Fig.6 Relationship between Q板/(gHs3)0.5and P/H'c

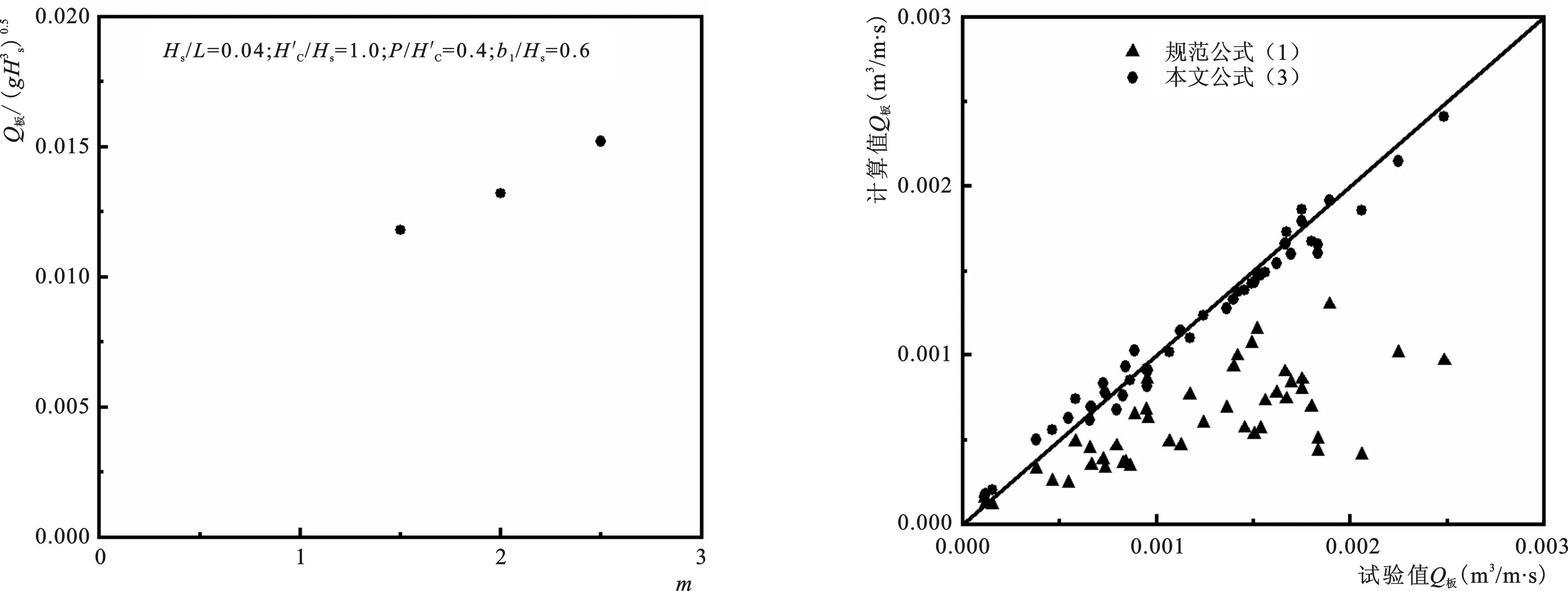
图7 Q板/(gHs3)0.5与m之间的关系Fig.7 Relationship between Q板/(gHs3)0.5and m图8 计算值Q板与试验值Q板之间的对比Fig.8 Comparison between calculated values Q板and measured values Q板

3 扭王字块体斜坡堤护面结构影响系数试验结果

本文综合了坡度、相对坡肩宽度、波陡、相对块体尺寸、相对胸墙高度、相对水深和相对堤顶超高等诸多因素，基于π定理，给出扭王字块体斜坡堤KAW的关系式如下

(4)

式中：KAW表示扭王字块斜坡堤的护面结构影响系数，等于在试验工况相同的情况下扭王字块体斜坡堤越浪量与光滑混凝土板斜坡堤越浪量的比值。

3.1 KAW与Hs/L之间的关系

依据单一变量法，其他因素不变，不同Hs/L对应的KAW结果如图9， 当Hs/L增大时，KAW减小，表现为指数关系。

3.2 KAW与d/Hs之间的关系

依据单一变量法，其他因素不变，不同d/Hs对应的KAW结果如图10，当d/Hs增加时，KAW减小，表现为指数关系。

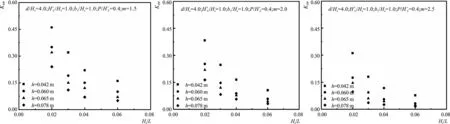
图9 KAW与Hs/L之间的关系Fig.9 Relationship between KAW and Hs/L

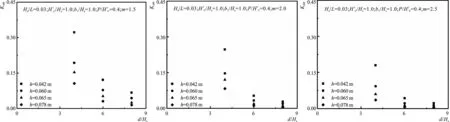
图10 KAW与d/Hs之间的关系Fig.10 Relationship between KAW and d/Hs

3.3 KAW与之间的关系

图11 KAW与H'c/Hs之间的关系Fig.11 Relationship between and KAWH'c/Hs

3.4 KAW与b1/Hs之间的关系

依据单一变量法，其他因素不变，不同b1/Hs对应的KAW结果如图12， 当b1/Hs增加时，KAW减小，表现为指数关系。

3.5 KAW与之间的关系

3.6 KAW与h/Hs之间的关系

依据单一变量法，其他因素不变，不同h/Hs对应的KAW结果如图14， 当h/Hs增加时，KAW减小，表现为指数关系。

规范[11]中用一常数表示一种块体的护面结构影响系数，而从本文看出，扭王字块体的护面结构影响系数不仅与波浪要素和堤身结构有关，而且受块体几何尺寸的影响，并不是不变的常数，这与孙大鹏[8]得出的结论一致。

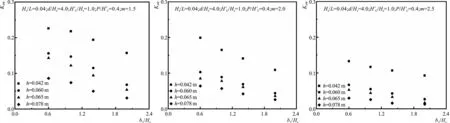
图12 KAW与b1/Hs之间的关系Fig.12 Relationship between KAW and b1/Hs

图13 KAW与P/H'c之间的关系Fig.13 Relationship between KAW and P/H'c

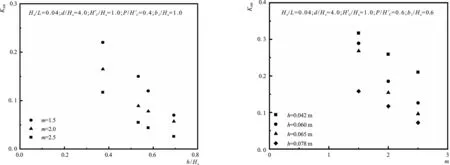
图14 KAW与h/Hs之间的关系Fig.14 Relationship between KAW and h/Hs 图15 m与KAW的关系Fig.15 Relationship between m and KAW

3.7 坡度系数m与KAW的关系

依据单一变量法，其他因素不变，不同坡度系数m对应的KAW结果如图15，在1.5≤m≤2.5范围内，KAW随m的增加而减小，呈指数衰减。

规范[11]中同种块体型式的护面结构影响系数只用一常数来表示。由图15可以看出，当坡度不同时，KAW并不是不变的常数，且具有随着坡度系数m的增大呈指数减小的趋势，即m也是KAW的一个重要影响因素，这是本文颇具新意的试验发现。

3.8 扭王字块体斜坡堤护面结构影响系数的计算关系式

(5)

图16为公式(5)的计算值与本文试验值的对比，相关系数R>0.98，表明公式(5)的精度较好。

4 扭王字块体护面斜坡堤越浪量的计算关系式

本文较全面的考虑了影响斜坡堤越浪量的主要因素，包括坡度、相对坡肩宽度、波陡、相对块体尺寸、相对胸墙高度、相对水深和相对堤顶超高等，延续规范[11]的编制思路，给出无因次扭王字块体斜坡堤平均越浪量的关系式

(6)

式中：Q表示单位时间单位堤宽的平均越浪量，m3/m·s；计算KAW时以公式(5)为准。

本文公式(6)计算出的越浪量与物模试验值对比如图17所示，相关系数R>0.98，说明本文公式(6)的精度较好。

图16 计算值KAW与试验值KAW对比Fig.16 Comparison between calculated values KAWand measured values KAW图17 计算值Q与试验值Q对比Fig.17 Comparison between calculated values Qand measured values Q

本文选取了两种坡度的物模试验工况进行公式的适用性验证，包括许凡[13](m=1.5)的物模试验工况及范红霞[6](m=2.0)的试验工况。应用本文公式(6)计算出的越浪量与试验值的比较如表2、表3所示。

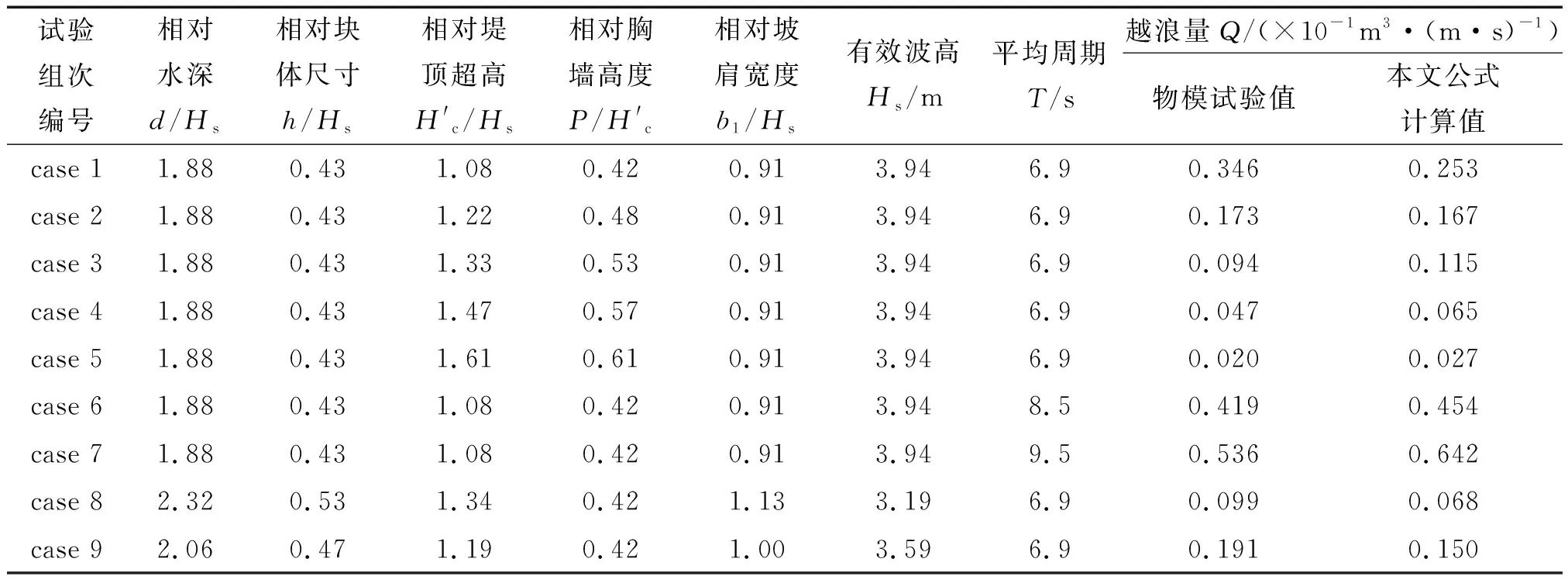
表2 本文公式计算值与许凡[13]物模值的对比(m=1.5)Tab.2 Comparisons between results of this paper and Xu[13](m=1.5)

表3 本文公式计算值与范红霞[6]物模值的对比(m=2.0)Tab.3 Comparisons between results of this paper and Fan[6](m=2.0)

由表2及表3可知，由于本文较全面的考虑了斜坡堤越浪量的影响因素，分析给出的越浪量公式计算值与许凡[13](m=1.5)、范红霞[6](m=2.0)的物模试验值吻合较好，表明本文的越浪量公式具有较好的适用性及较高的计算精度。

5 结论

(1)规范[11]中将相同块体、不同坡度下的护面结构影响系数取为常数，本文通过研究，发现护面结构影响系数随坡度系数m的增大而减小，并非是不变的常数，即坡度亦是护面结构影响系数的主要影响因素之一，这是本文新的试验认知。

(2)规范[11]中将相同块体的护面结构影响系数取为常数，通过本文的试验研究结果发现，扭王字块体斜坡堤的护面结构影响系数受多种因素的影响，包括波浪要素、堤身结构和相对块体尺寸等，这一认知同孙大鹏[8]的试验结论一致。

(3)基于作者前期[8]和本次的物模试验，成果表明：对于具有胸墙的扭王字块斜坡堤的越浪量，应视坡度、相对坡肩宽度、波陡、相对块体尺寸、相对胸墙高度、相对水深和相对堤顶超高为其主要影响因素。

(4)本文较为全面的考虑了影响斜坡堤越浪量的因素，包括坡度、相对坡肩宽度、波陡、相对块体尺寸、相对胸墙高度、相对水深和相对堤顶超高等，基于单一变量的分析方法，采用非线性拟合给出了扭王字块体斜坡堤护面结构影响系数计算关系式和平均越浪量的计算关系式，通过与许凡[13](m=1.5)、范红霞[6](m=2.0)的物理模型试验值的对比验证，表明本文公式有较好适用性和较高的计算精度，试验成果补充了规范[11]条文，也为扭王字块体护面斜坡堤的设计和实际工程应用提供了参考依据。