面向实际运行的战略航班时刻优化技术

柯雨辰， 胡明华， 杨 磊， 赵 征

(南京航空航天大学民航学院， 南京 211106)

航班时刻既是民航运输业重要的资源，也是航空运输企业的立足之本。同时，作为治理延误和实施空中交通流量管理最重要的基础数据，寻找一个合适的角度对其进行优化，可以在机场需求管理中起到事半功倍的效果。Zografos等[1]以最小化申请时刻和实际分配时刻之间的差异为目标，提出了一种可以对整个航季优化的航班时刻优化模型；Jacquillat等[2]提出一种综合方法，共同优化机场在战略层面的航班时刻表和战术层面的机场容量利用率；Corolli等[3]考虑了航空公司运营偏好以及机场网络结构，提出了一种两阶段的随机规划模型对时隙进行分配；Pellegrini等[4]提出了一种模型，应用国际航空运输协会现有的规则和做法，能同时在所有欧洲机场分配航班时刻；Zografos[5]等针对单机场开发并解决了一种同时考虑效率性和公平性的双目标时隙分配模型；王飞等[6]以航班正点率、旅客延误时间、延误成本、基尼系数等目标的不同组合为优化目标建立航班时刻优化模型；罗亮[7]建立了基于航路资源分配的航班时刻优化模型；裴一麟[8]考虑航空公司收益，对航线网络和航班时刻建立了双层规划模型；汪梦蝶等[9]提出可接受调整水平的概念，建立了基于功效性和可接受性的双目标航班时刻优化模型；李昂等[10]以京津冀机场群为研究对象，构建提升航班正点率的航班时刻优化模型。

上述研究从航空公司偏好、效率性和公平性等具有现实意义的角度出发，在降低延误、缓解机场拥堵方面取得了一定的成果，但没有结合航班起降后的实际运行情况进行优化。现将停机位、跑道及终端区的进出走廊口作为一个系统来研究，将跑道和走廊口看作系统内的受限单元，通过滑行时间和飞行时间对系统关键节点建立连接并根据资源能力限制进行约束，从而减少飞机在跑道头的排队等待时间以及走廊口因为流控而造成的航班延误。

1 问题描述及模型假设

所要解决的问题可以简述如下：首先，以停机位、跑道和终端区进出走廊口构成的系统为研究对象；其次，考虑航班在系统中的运行流程，计算航班经过跑道和走廊口的时间节点，如图1所示；最后，根据受限单元的资源能力，即跑道运行容量和走廊口通行能力对关键时间节点的航班量进行限制，在满足容流匹配的前提下通过小幅度的调整为每个航班分配一个最优的起降时刻，从而提高机场运行效率、降低延误。

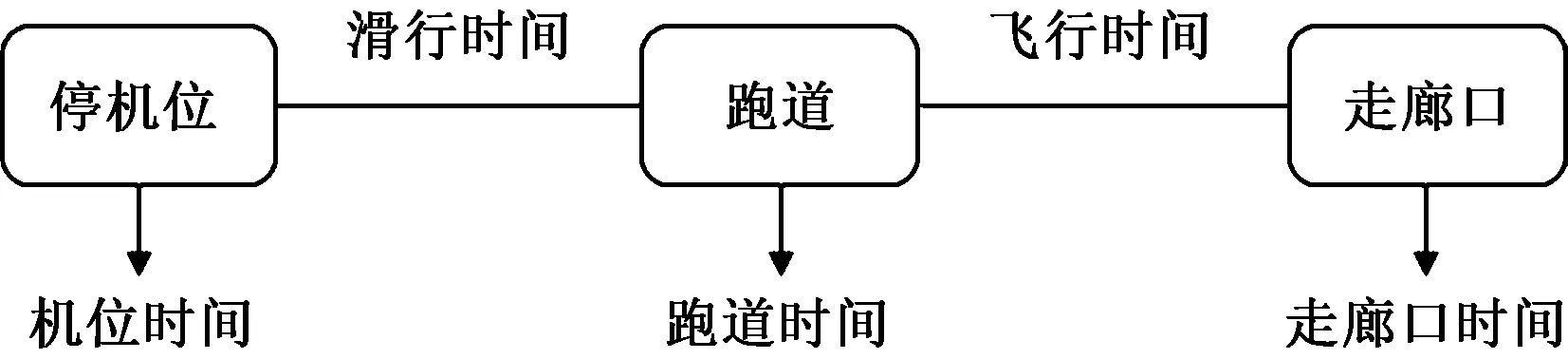
图1 航班在所研究系统中运行流程

在建立相关模型之前，为了使得问题更严谨求解更方便进行如下假设说明。

假设1在实际应用中航班时刻不是一个精确、具体的时间点，而是一段特定时隙。同一机场时隙长度相同，通常设定为5 min。一个时隙内可以起降多个航班，即根据机场的服务能力设定时隙容量。

假设2根据《民航时刻管理办法》总则第二条规定“航班时刻的时间基于挡轮挡时间和撤轮挡时间”，将某一航班分配到的航班时刻看作是该航班的轮挡时间，即机位时间。

假设3将优化前航班时刻表中各公司分配的航班时刻视作航空公司所申请的即期望获得的时刻，并认为各公司所能接受的最大调整量相同。

假设4本文中考虑的实际运行场景中，跑道运行模式的设定是固定的。各个航班所分配到的起降跑道根据走廊口进行匹配。

假设5由于战略阶段在换季航班时刻表中无法为每个航班分配具体的停机位，滑行时间的计算从该航班的历史运行数据中进行挖掘。根据该航班的历史停放机位和使用跑道信息，匹配相应的滑行时间并进行平均，取平均值代表该航班的滑行时间。

假设6航班在终端区内的飞行时间，即航班在跑道和走廊口之间的飞行时间通过仿真软件模拟运行得到。为此选用浦东机场为研究对象，经过仿真得到走廊口和跑道对应的飞行时间如表1所示。

假设7联程航班必须保证有充足的过站时间上下客和进行地面保障服务，现忽略机型对模型和算法的影响，对于联程航班设定统一的最小过站时间。

2 航班时刻优化模型

2.1 决策变量

由于本文模型关注的是受限单元在各自对应的时间节点下的容流匹配关系，为了便于约束条件使用数学表达式进行说明，在此设立三组决策变量，分别与时间节点有关，即

(1)

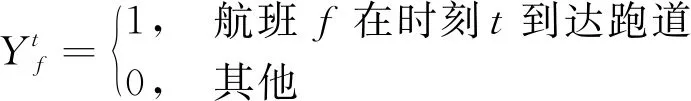
(2)

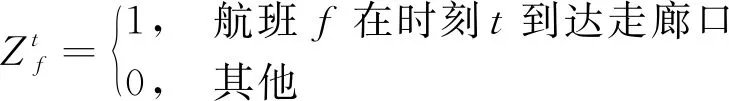
(3)

2.2 约束条件

(1)每个航班只能分配到一个时间片，即

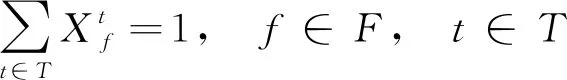
(4)

式(4)中；T为时间片集合，T={1,2，…，Tn}；t∈T；F为所有航班集合，f∈F。

式(4)表示每个航班在1 d内有且只能分配到一个时刻，保证没有航班被拒绝。

(2)每个航班必须满足最大调整量约束，即

|t-tf|≤tmax，t∈T

(5)

式(5)中：tf为航班f原计划申请的时间片，f∈F,tf∈T；tmax为航班的最大允许调整量。

式(5)表示每个航班在时刻分配过程中有一个最大允许调整量，是航空承运人可以接受的一个时刻偏移范围。

(3)过站航班要满足最小过站时间约束，即

(fa,fd)∈P,k∈[tf,h)，t∈T

(6)

式(6)中：fa和fd表示航班为进港航班和离港航班；P为过站航班对集合；tad为航班对最小过站时间；h为时刻集合中的最后一个时刻。

式(6)表示过站航班要满足最小过站时长。

(4)跑道运行容量限制，即

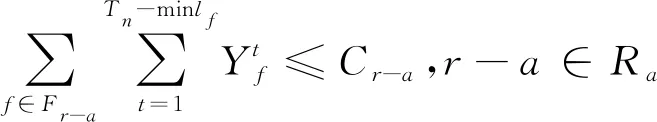
(7)

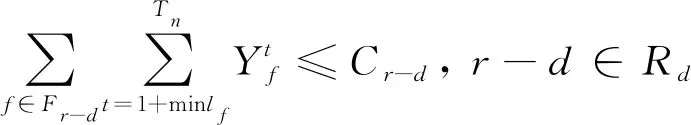
(8)

式中：R为机场跑道集合；Ra为机场内用于进场航班的跑道集合；Rd为机场内用于离场航班的场跑道集合；Fr-a为使用进场跑道r-a的航班集合，r-a∈Ra；Fr-d为使用离场跑道r-d的航班集合，r-d∈Rd；Cr-a为进场跑道r-a的运行容量限制；Cr-d为离场跑道r-d的运行容量限制;lf为所有航班的滑行时间集合。

式(7)、式(8)表示分别对进场跑道和离场跑道运行容量进行约束。《机场时刻容量评估技术规范》中规定容量评估时选用的单位为小时，为了防止出现一小时内流量分布不均，在此设置容量限制的区间长度为15 min和60 min。

(5)走廊口通行能力限制，即

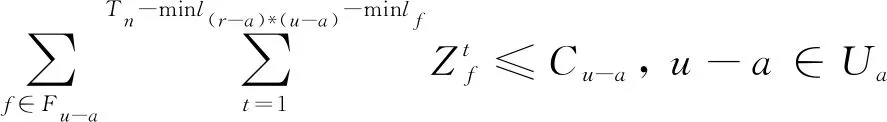
(9)

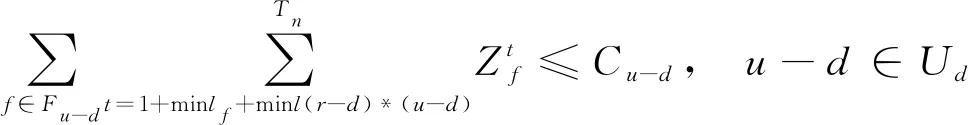
(10)

式中：U为机场终端区走廊口集合；Ua为到达走廊口集合；Ud为出发走廊口集合；Fu-a为使用到达走廊口u-a的航班集合，u-a∈Ua；Fu-d为使用出发走廊口u-d的航班集合，u-d∈Ud；Cu-a为出到达廊口u-a的通行能力；Cu-d为出发走廊口u-d的通行能力；lr*u为终端区飞行时间集合，r*u表示跑道r和走廊口u之间的飞行时间，r∈R，u∈U。

式(9)和式(10)根据走廊口通行能力分别对到达走廊口和出发走廊口进行容量约束。由于管制单位为了对飞行流量进行更加精细化的管理，对于走廊口通常会设置5 min区间的流量限制，因此设置走廊口容量限制的区间长度为5、15和60 min。

2.3 目标函数

本文中研究的优化技术是基于机场的角度，作为服务方的机场应当尽量满足用户即航班承运人的需求。因此，在考虑航空公司偏好的前提下，调整过程中使得优化后的航班时刻尽可能少的偏离航空公司请求的时刻。从效率性角度出发，同时由于多重约束下的调整难度，以最小化总的航班时刻偏移量为目标函数，其表达式为

(11)

3 求解算法及实例验证

3.1 模型求解算法

为确保容量约束的平滑性和紧致性，设计了以5 min为步长的滑动时间窗，以满足连续小时和15 min约束。由于变量空间较大，针对问题规模的复杂性，设计了面向精确解的高效最优化算法，采用MATLAB中的线性整数规划工具箱intlinprog进行编程求解。

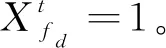
Step2构建系数矩阵。构建目标函数的系数矩阵，根据航班可接受的前后最大偏移量建立不等式约束条件和等式约束条件的系数矩阵，最后将系数矩阵和变量参数输入工具箱进行求解。

3.2 算例分析

本文中采用的数据来源于《2019冬春浦东机场班期时刻表》，以航班量最大的周三为例开展优化。需要说明的是，在本文中跑道设定为北向运行，即离场跑道为34L和35R，进场跑道为34R和35L，每架航班所使用的跑道根据走廊口进行匹配。统计表明，在班期计划周三这一天，共有计划起降航班1 529架次，其中离港航班764架次，进港航班765架次。经过仿真得到浦东机场走廊口和跑道对应的飞行时间如表1所示。

航班信息以及优化前后的部分航班时刻如表2所示。优化前跑道和走廊口存在超过容量限制的情形，而优化后所有跑道和走廊口均能满足各种时间区间长度下的容量限制约束，从而达到容流匹配的效果。以流量较多的进场跑道34R和离场走廊口PIKAS进行说明：优化前以15 min和60 min为区间划分时间片，34R跑道分别有4个和3个时间片超出对应区间容量限制；优化前以5、15和60 min为区间划分时间片，PIKAS分别有9、6、0个时间片超出对应区间容量限制；优化后，不论是跑道还是走廊口，各时间片均能满足容量限制约束。下文对航班调整情况进行具体分析，同时借助仿真软件评估优化后运行效率是否得到改善，以验证模型的有效性。

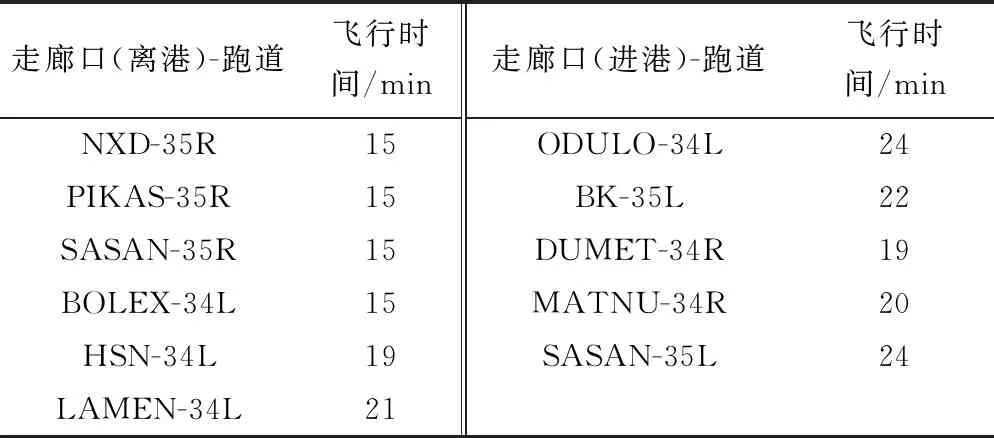
表1 走廊口飞行时间统计

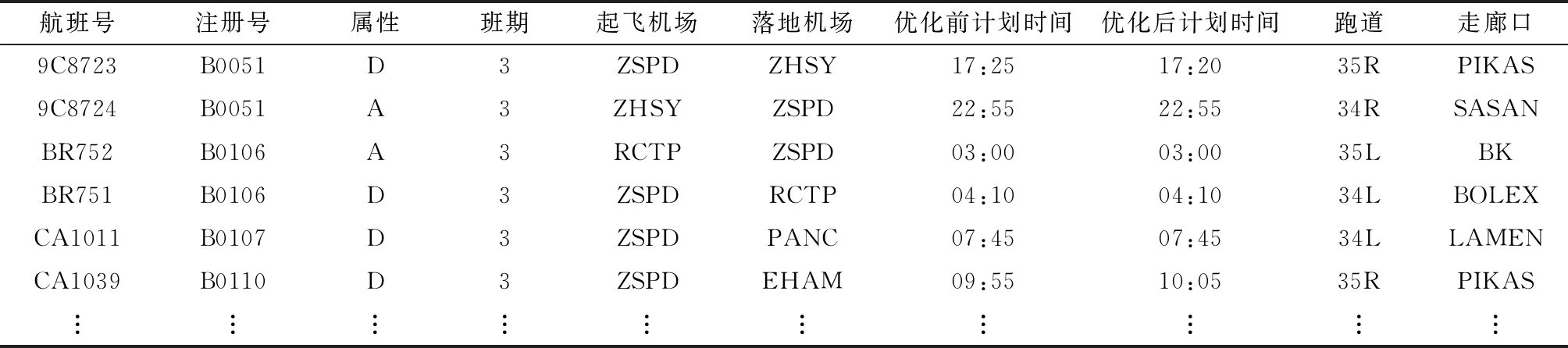
表2 优化前后航班时刻表信息

3.2.1 航班时刻调整量分析

以5 min时间片为单位，将一天划分为288个时间片，航班时隙最大允许偏移量为1 h，即可以前后移动12个时间片。进行全局优化调整后，共调整航班295架次，其中进港航班127架次，离港航班168架次。图2是航班时刻偏移量的分布情况，横坐标是可能的航班偏移量，纵坐标是该时刻偏移量大小对应的航班调整数目。

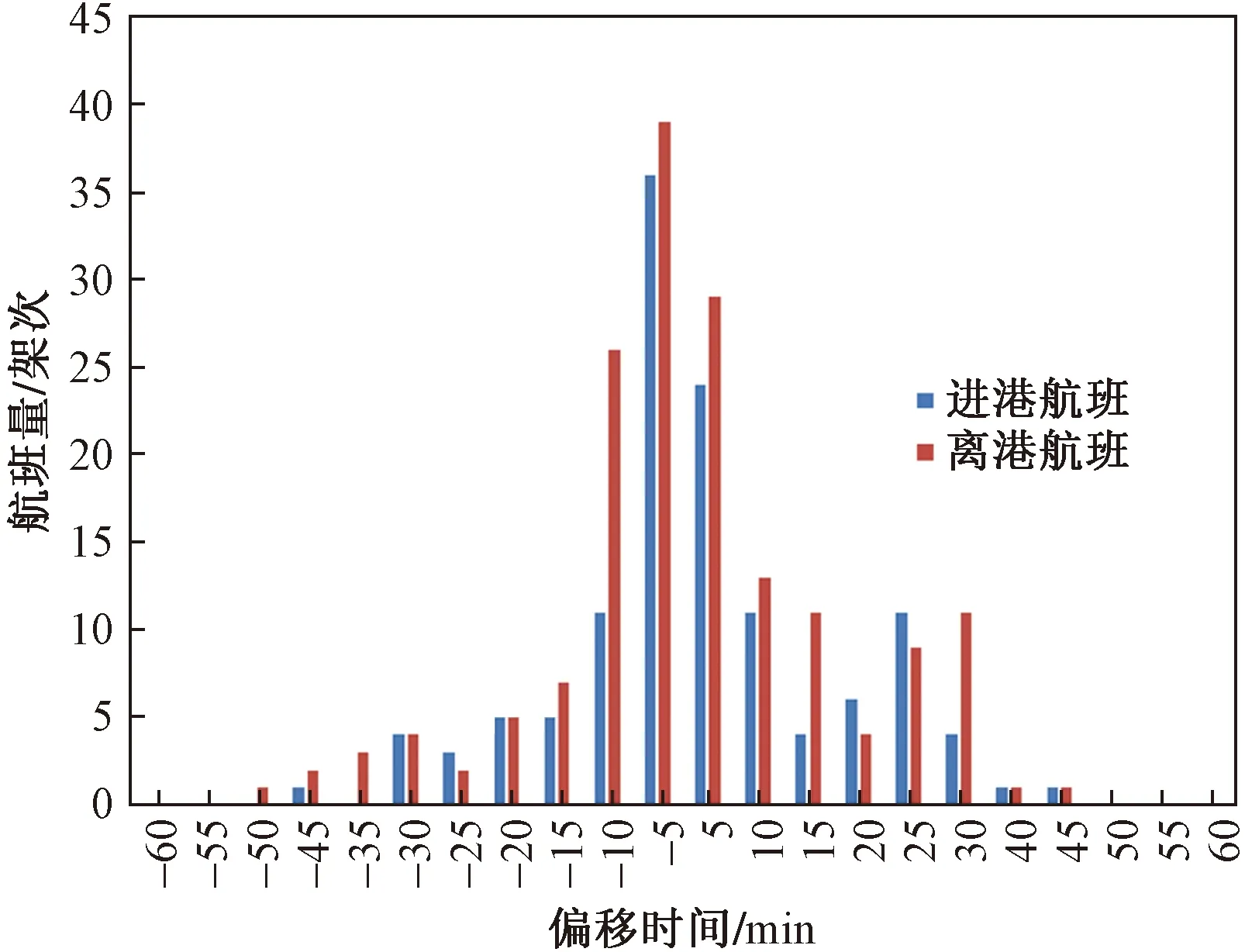
图2 航班时刻偏移量分布

由图2可知，时刻调整范围从-50 min跨越至45 min，最大时刻偏移量的绝对值为50 min，在各公司的最大调整接受范围内。其中多数航班的时刻偏移量集中在柱状图的中段位置，说明大部分航班的偏移量较小。进一步作出偏移量绝对值的直方图。如图3所示，总体来说，约80%的航班仅需前后调整3个时间片(15 min)。众所周知，时刻是一种资源且具有一定的价值，较小的调整幅度，不仅使得航空承运人的偏好得到最大程度的满足，同时保障了航班的时刻利益。

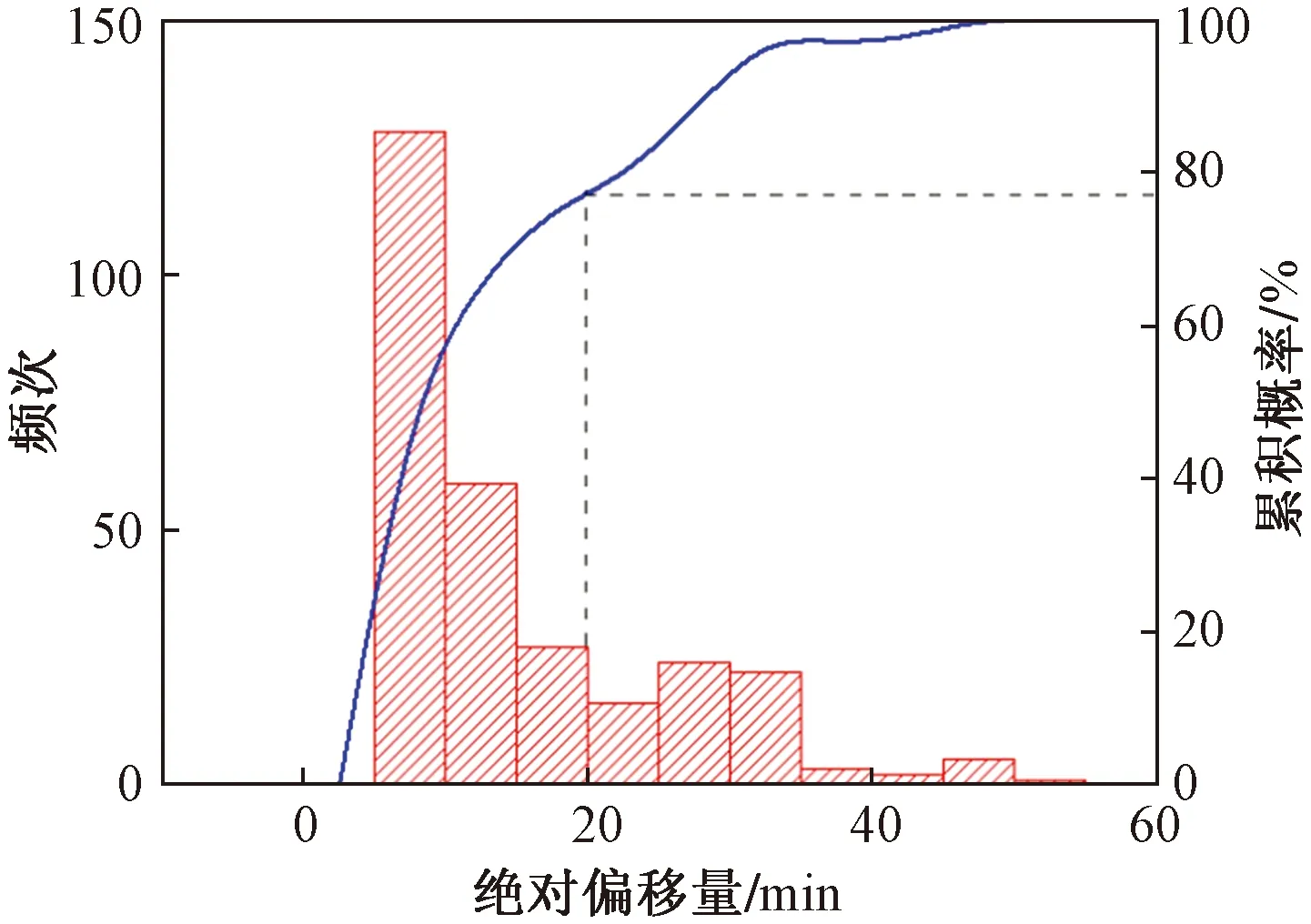
图3 时刻偏移量直方图

3.2.2 基于AirTop的模型仿真验证分析

对优化前后的班期时刻表使用AirTop软件进行仿真验证，作出优化前后的平均进离场延误与流量分布图，如图4所示。由图4(a)可知，优化前05：00—07：00的离场延误较为严重，延误伴随着航班量的增加而增大，当流量增大至趋于稳定时延误开始递减，随即在午时随着流量轻微的增加又出现一个小高峰；进场延误较小且较为稳定。由图4(b)可知，优化后各个小时的离场延误变化趋势和优化前相似，但高峰值明显降低，进场延误仍保持较小，不作讨论。

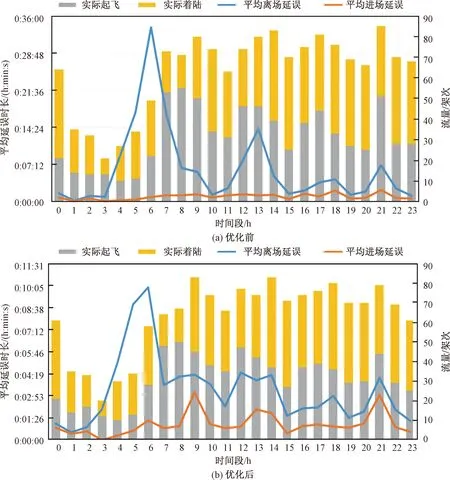
图4 优化后平均进离场延误与流量分布

为了从数值上更清晰的对优化前后的离场延误变化进行比较，将优化前后的延误分布至于同一坐标系下，如图5所示，一天的延误水平有明显改善，尤其是高峰延误经过优化后大大降低。最后由表1中列出的优化前后仿真运行指标数据对运行效率进行评估。

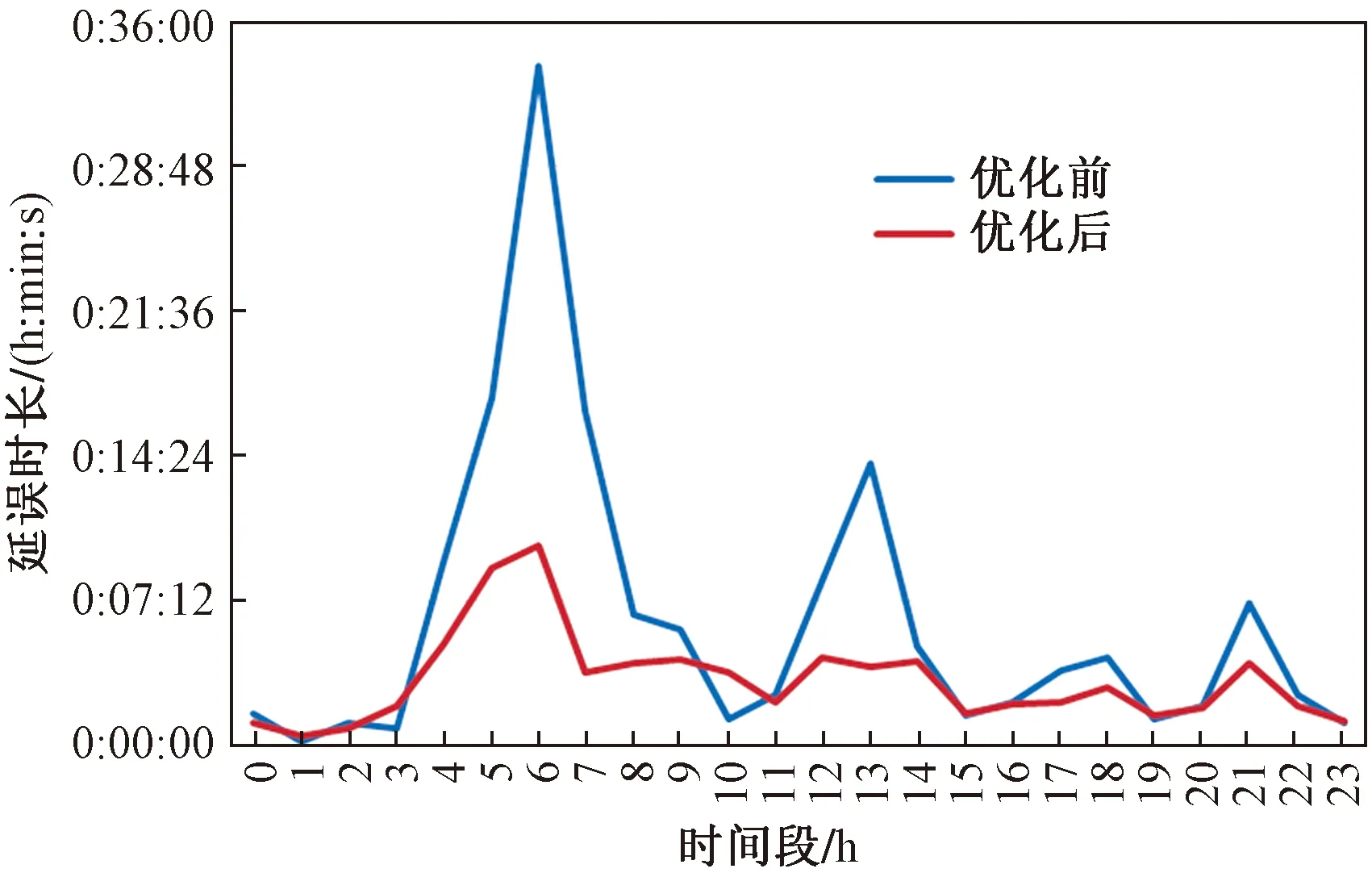
图5 优化前后离港延误分布对比

仿真结果数据有力验证了所建立的航班时刻优化模型的有效性。如表3所示，对比优化前后，平均离场延误从6.5 min降低至3.3 min，降低了49%左右；高峰离场延误从33 min降低为10 min，降低了69%左右；平均滑行延误从6 min降低为2 min，降低了2/3；平均放行正常率从72.38%增加至81.42%，增加了12%左右。由上述指标变化可知，航班运行效率得到了极大的改善，尤其是延误水平显著降低。因此，本文中所建立的模型是有效的。

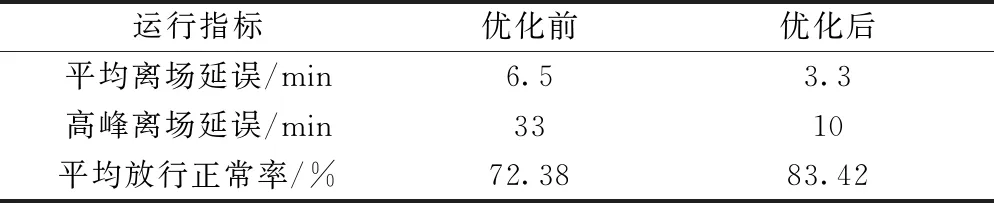
表3 优化前后运行指标数值

4 结论

以航班时刻为研究对象，从时间和空间两个维度考虑了航班在所研究系统内的实际运行情况，建立了面向实际运行的战略航班时刻优化模型。以浦东机场班期时刻表数据进行实例验证，得到以下结论。

(1)通过对约20%的航班时刻进行微调，优化后的时刻表完全满足了跑道和走廊口的容流匹配限制。

(2)配合AirTop软件进行仿真验证，证明该模型能够有效降低航班延误水平、提高放行正常率。

由于本文的优化围绕单机场展开，在未来研究中，可以将研究范围扩展至终端区多机场协调问题作进一步探讨。