基于K近邻互信息估计的原油管道电耗预测
李 雨,侯 磊,徐 磊,白小众,刘金海,孙 欣,谷文渊
(1.中国石油大学(北京)石油工程教育部重点实验室,北京 102200; 2.中国石油天然气集团公司油气储运重点实验室,北京 102200; 3.国家管网集团北方管道有限责任公司锦州输油气分公司,辽宁 锦州 121000)
自上世纪起,我国学者开始进行输油管道运行电耗的相关研究并分析影响管道电耗的重要因素。管道周转量、进出站压力、进出站温度和土壤温度等特征都被认为是影响管道电耗的重要因素[1-5]。由于每条管线运行工况不同,不同因素影响管道电耗的程度亦不同。有的仅利用日输量便可比较准确地预测管道运行电耗[6],也有的需要同时考虑多个特征才能实现管道电耗的准确预测[7]。针对第二种情况,不但需要生成一些设备无法直接测量的特征,以扩大待选特征范围,还需要利用合理的算法来确定更适合被用来预测管道电耗的特征。为确定一个能够最精确预测管道电耗的小特征集合,需要对全部待选特征进行相关性分析。进行相关性分析的方法有皮尔逊系数法[8]和互信息法[9-10]。但是皮尔逊系数在评价两个正态分布特征之间的线性关系时才会有很好的效果,而对非线性关系不敏感[11]。互信息虽然没有上述问题,但需要计算特征的概率密度函数[12-13]。管道运行特征间非线性强,且多为离散数据,不宜计算概率密度函数,直接使用上述两种方法效果不好,需要进行改进。Kraskov[14]提出基于K近邻的互信息估计方法,一定程度上解决了互信息过度依赖特征分布规律的缺陷。K近邻互信息估计不需要计算概率密度函数,只需要计算不同特征之间的欧氏距离便能估算出两个特征之间的互信息值。本研究利用原油管道输送相关公式扩充原始数据集,将K近邻互信息估计和BPNN结合,提出一种原油管道电耗预测模型,并利用某原油管道三年运行数据验证该模型预测效果。
1 数据来源
全部数据由原始数据和生成数据两部分组成,共包括管道运行、油品物性、环境状况、设备工况四个方面。其中扩充数据由原始数据通过管道输送理论公式计算得来。
1.1 原始数据
该类数据源于某段原油管道2016年至2019年运行报表,共911组数据。每组数据包括日输量、出站压力、出站温度以及地温等21个特征。该段管道尺寸为φ508×7.1,全长为55.2 km,年设计输量为107t,设计压力为5 MPa,中间无其他站场。
1.2 扩充数据
原始数据并未覆盖可能与管道电耗相关的全部特征,因此需要对原始数据进行扩充。同时,新生成的强相关性特征也可以被认为是学习任务的中间概念,这种中间概念越多,往往越有利于建立精确的管道电耗预测模型[15]。利用已有管道输送理论公式计算出多个与原油输送相关的特征,如表征流体流动情况的雷诺数Re、衡量换热情况的传热系数K、苏霍夫温降公式中的参数a以及进出站压差等特征。在式(1)、(2)中分别列出雷诺数Re和苏霍夫温降公式中参数a的计算公式
Re=ρvd/μ
(1)
(2)
式中ρ——油品密度/kg·m-3;
v——油品流速/m·s-1;
d——管道内径/m;
μ——油品动力黏度/Pa·s;
K——传热系数/W·(m2·℃)-1;
D——管道外径/m;
G——管道输送油品的质量流量/t·d-1;
C——油品热容/J·(kg·℃)-1。
共得到31个特征见表1。按照训练集和测试集比例为4∶1对911组数据进行划分,得到训练集数据728个,测试集数据183个。
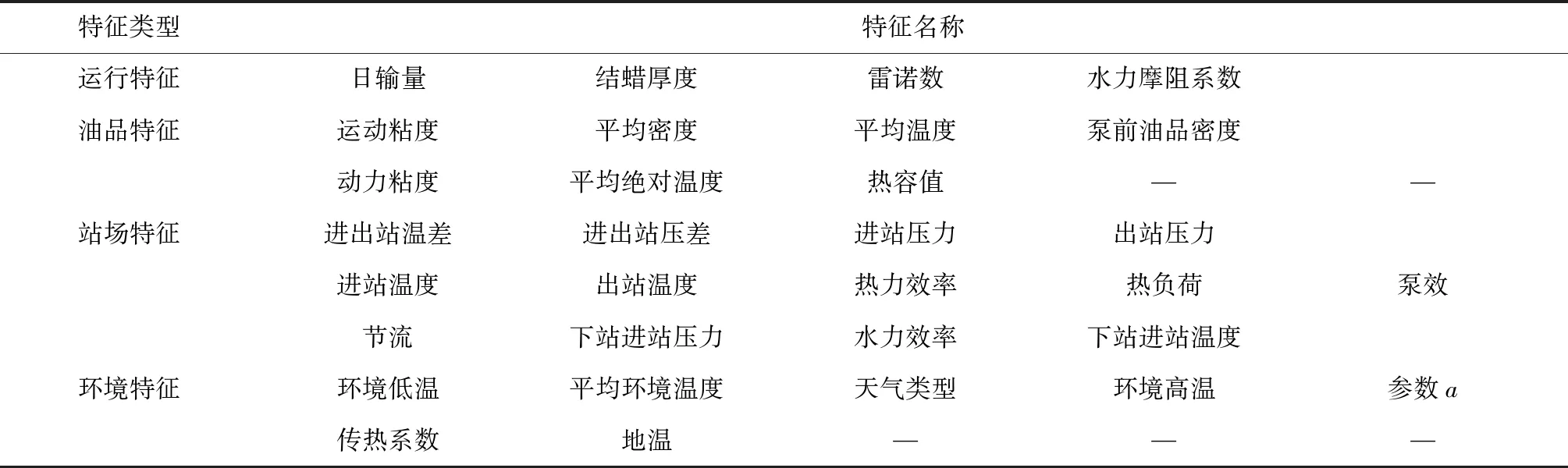
表1 31个特征名称表
3 原理与方法
3.1 K近邻互信息估计
引入K近邻互信息估计(K-EMI)[14]计算特征间的相关性。K-EMI在评价复杂非线性关系时有较好的效果,并且不需要计算离散数据的概率密度。
管道运行数据集共含911组数据,每组数据拥有31个特征。数据集用D={X1,X2,X3,……,X31}来代表,Xi={xi1,xi2,xi3,……,xi911}。令管道电耗为特征Y,则每个特征Xi和管道电耗Y张成一组向量空间。设Zij为特征Xi和Y空间中的第j个点,则有Zij=(xij,Y)。某点Z和其他点Z′之间的距离d的计算公式为[15]
d=||Z-Z′||=max{||x-x′||,||Y-Y′||}
(3)
其中,||Y-Y′||和||x-x′||是同阶范数。手动确定K值后,点Zij到其最近的第K个点的欧式距离记作ε(i,j)/2,投影到X和Y的子平面上的距离分别为εx(i,j)/2和εy(i,j)/2。根据式(3),有ε(i,j)=max(εx(i,j),εy(i,j))。统计出在X和Y方向上到Z点欧氏距离小于ε(i,j)/2的点的个数,分别记为nx和ny。图1展示处于特征空间X和Y中的点如何确定nx和ny。其中深色点有nx=5,ny=4。

图1 K近邻互信息估计示意图
利用式(4)和式(5)计算特征Xi和Y之间的互信息
I(i)(Xi,Y)=ψ(K)-<ψ(nx+1)+
ψ(ny+1)>+ψ(N)
(4)
(5)
ψ是伽玛函数,满足ψ(x+1)=ψ(x)+1/x,ψ(1)=-0.577 216。特征间K-EMI结果的集合可表示为I={I(1)(X1,Y),I(2)(X2,Y),……,I(31)(X31,Y)}。K-EMI值越高,表示相关性越强。
3.2 BPNN
BPNN能够以任意精度逼近某一非线性函数,被广泛应用于建立预测模型。BPNN拓扑结构如图2所示,其中输入层和隐含层可包含多个神经元,不同层的神经元间利用权值W连接激活函数h为relu函数。神经网络通过修正权值来使模型平均均方误差(MSE)达到最小,达到提高模型预测精度的目的。本研究将不同特征作为BPNN输入,将电耗作为输出,建立单隐含层的电耗预测模型。
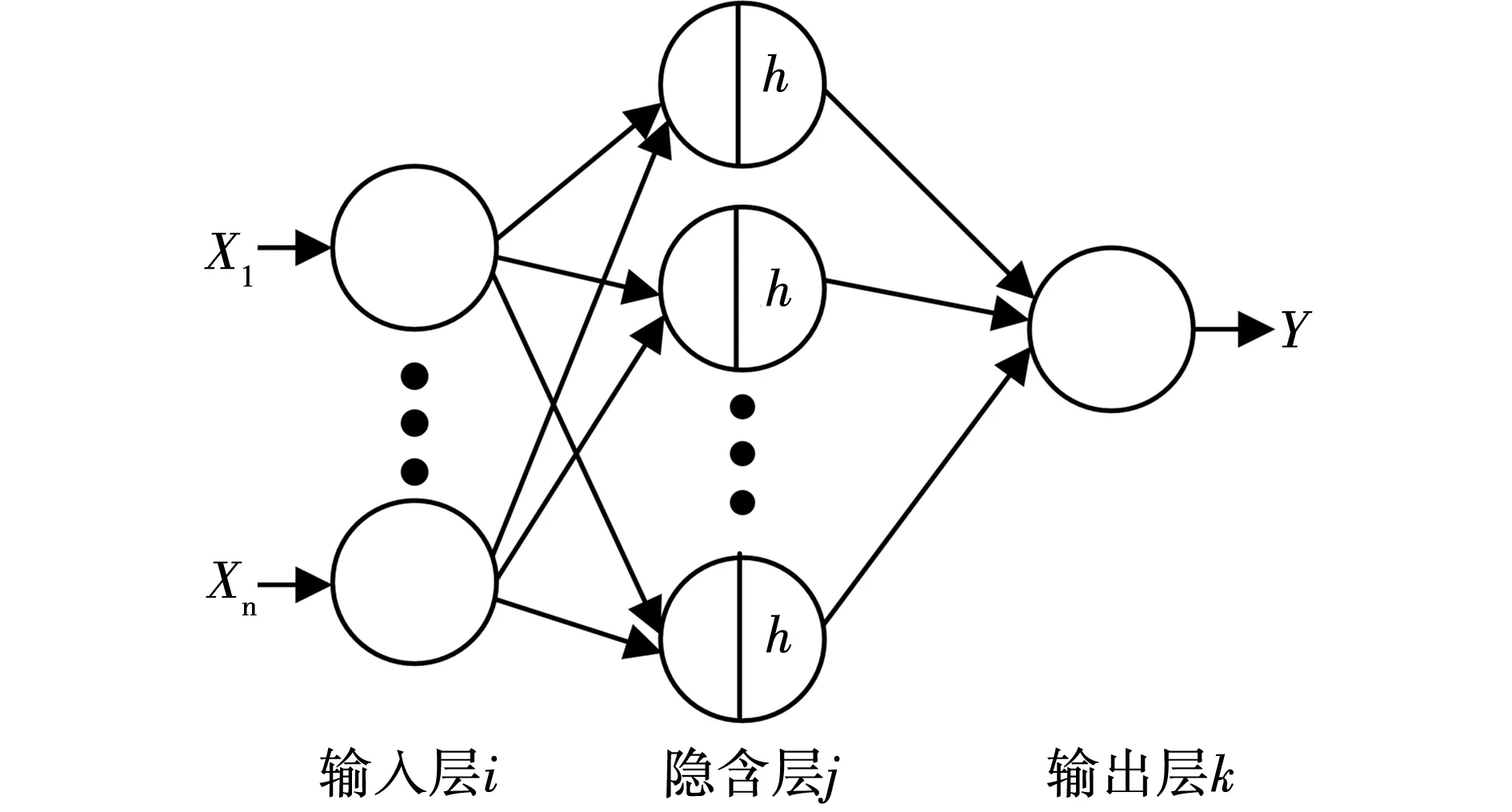
图2 单隐含层神经网络示意图
3.3 模型效果验证
为评价模型训练速度和预测精度,本研究采用建模时间作为评价模型训练速度的指标,采用均方根误差(RMSE)、决定系数(R2)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)作为衡量模型精度的指标,其计算公式如下
(6)
(7)
(8)
(9)

4 算例分析
采用Windows10系统,处理工具为Spyder软件,BPNN基于Keras第三方库建立。
4.1 建模流程
第一步利用原油加热输送和等温输送相关公式横向拓展数据集;第二步利用K-EMI选出与电耗相关性强的特征;第三步将选出的不同特征喂入BPNN以建立原油管道电耗预测模型;第四步利用3.3提到的四个误差指标验证神经网络模型的预测精度。图3展示了构建原油管道电耗预测模型的完整过程。
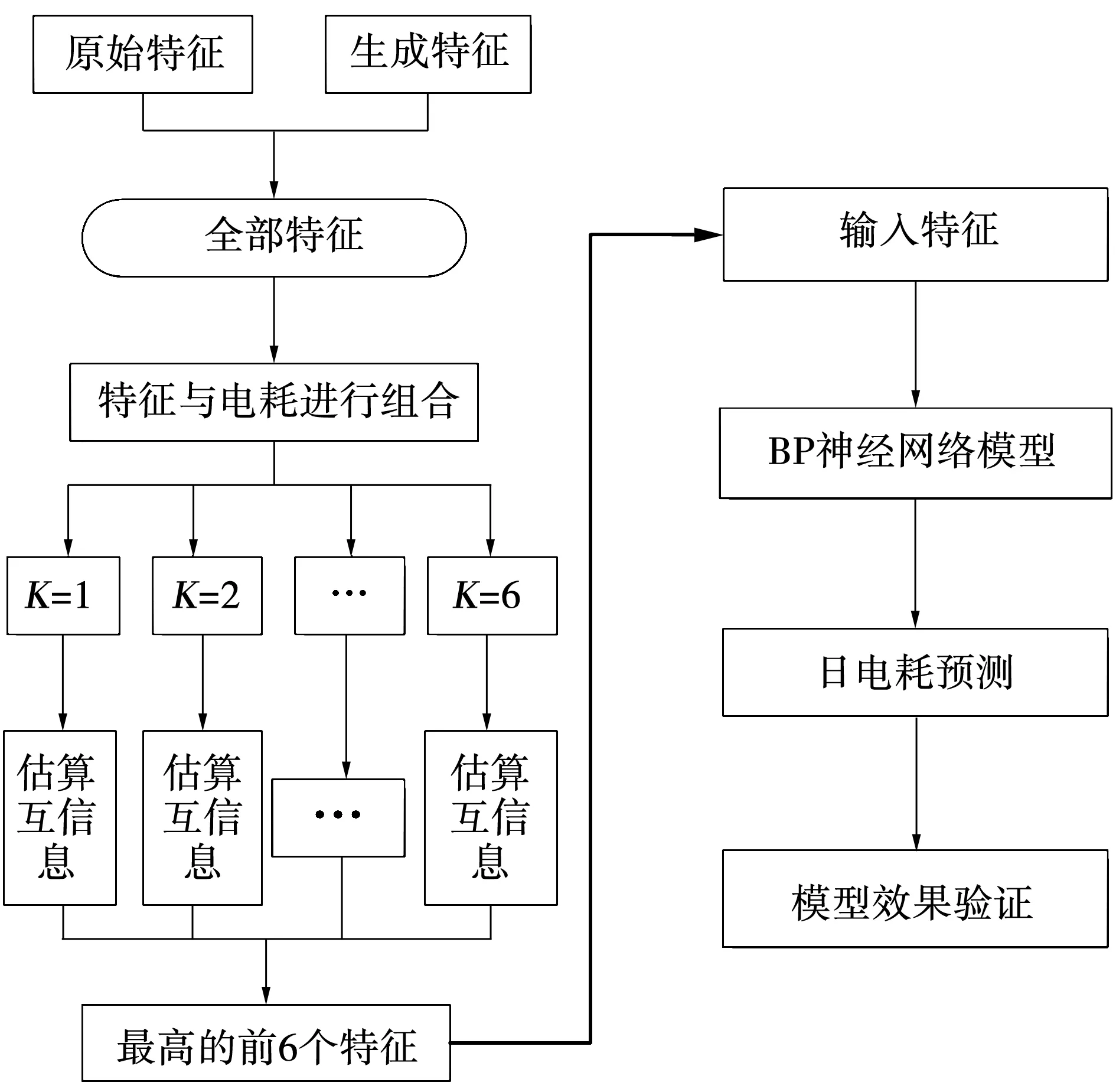
图3 方法概览
4.2 K-EMI结果
K-EMI的计算需要提前设定K值,当K值不同时,计算结果略有差异。本研究计算不同K值时模型的K-EMI结果以作对比,结果如表2所示。
观察表2能够发现,K取不同值时,特征T1~T6的K-EMI数值排位靠前且名次固定。选取T1~T6作为模型的备选输入特征。
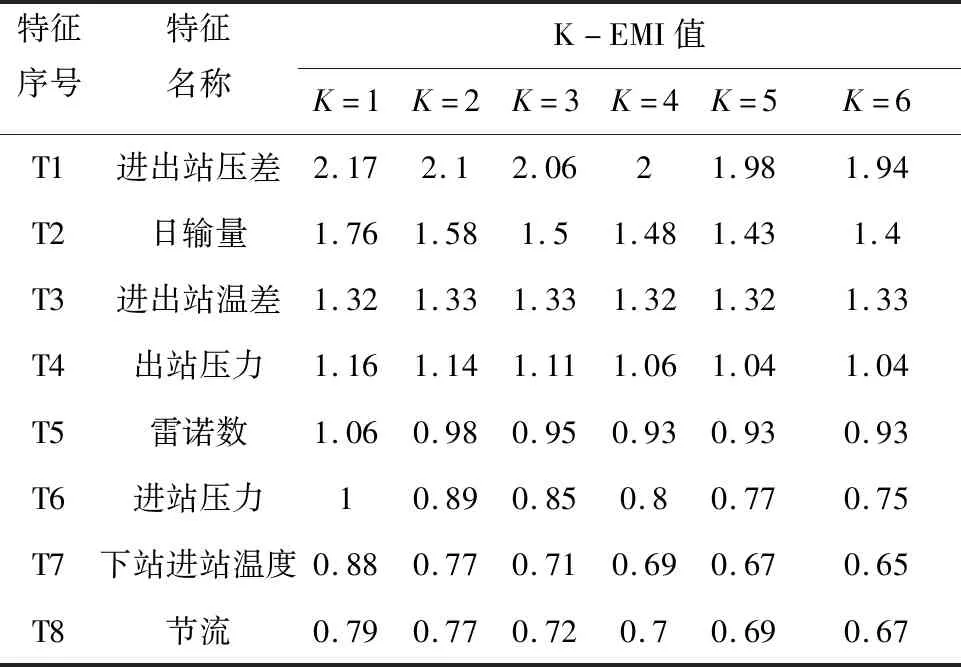
表2 不同K值时的K-EMI结果
为更直观地展示每个特征和管道电耗的分布规律,将纵坐标设为管道电耗,横坐标分别为不同特征,绘制特征T1~T8与电耗分布关系图,如图4所示,其中各点为数据实际位置分布,曲线为抛物线拟合结果。

图4 电耗与部分特征分布关系图
分析表2和图4发现:进出站压差、进出站温差和雷诺数等生成特征与管道电耗存在明显的非线性关系,说明在预测前先扩充数据集有利于找到更多与管道电耗存在强相关性的特征;衡量流动状况的雷诺数与运行电耗的相关性很强,衡量传热能力的传热系数却未出现在图表中,说明在很大程度上决定该管道电耗水平的是原油流动状况,而对流换热过程对管道电耗水平不起决定作用;压差与管道电耗的相关性强于进站压力、出站压力等压力参数,证明在输油过程中管道电耗主要用来通过离心泵给油品增加压头,增大外输压力;温度特征和油品运动黏度都未表现出与电耗的强相关性,这是由于温度特征不能直接影响管道电耗,只能通过改变油品黏度间接影响管道电耗。油品的运动黏度本身波动范围小且存在其他因素干扰,不能决定管道运行电耗,因此这些特征与电耗的相关性都很弱。
综上所述,通过相关性分析不但能够确定与电耗相关的特征,还能通过分析不同特征间相关性差异解释输油管道运行电耗变化。
4.3 模型预测结果
共建立9个BPNN模型,将K-EMI计算出的前1~6个与电耗相关性最强的特征作为输入得到1#~6#模型;将全部特征作为模型输入得到7#模型;将互信息计算出的前5个特征作为输入得到8#模型,将皮尔逊系数计算出的前5个特征作为输入得到9#模型。对比模型1#~7#以确定用来建模的最优特征数量,对比模型5#、8#和9#以分析不同相关性分析方法提取相同数量特征的效果。三种相关性分析方法提取出的特征集合如表3所示。

表3 不同相关性分析方法提取的特征集合
神经网络模型参数、30次重复实验的平均误差和平均训练时间如表4所示。根据模型的均方根误差(RMSE)、决定系数(R2)、平均绝对误差(MAE)和平均相对百分比误差(MAPE)结果绘制图5所示误差分布图。
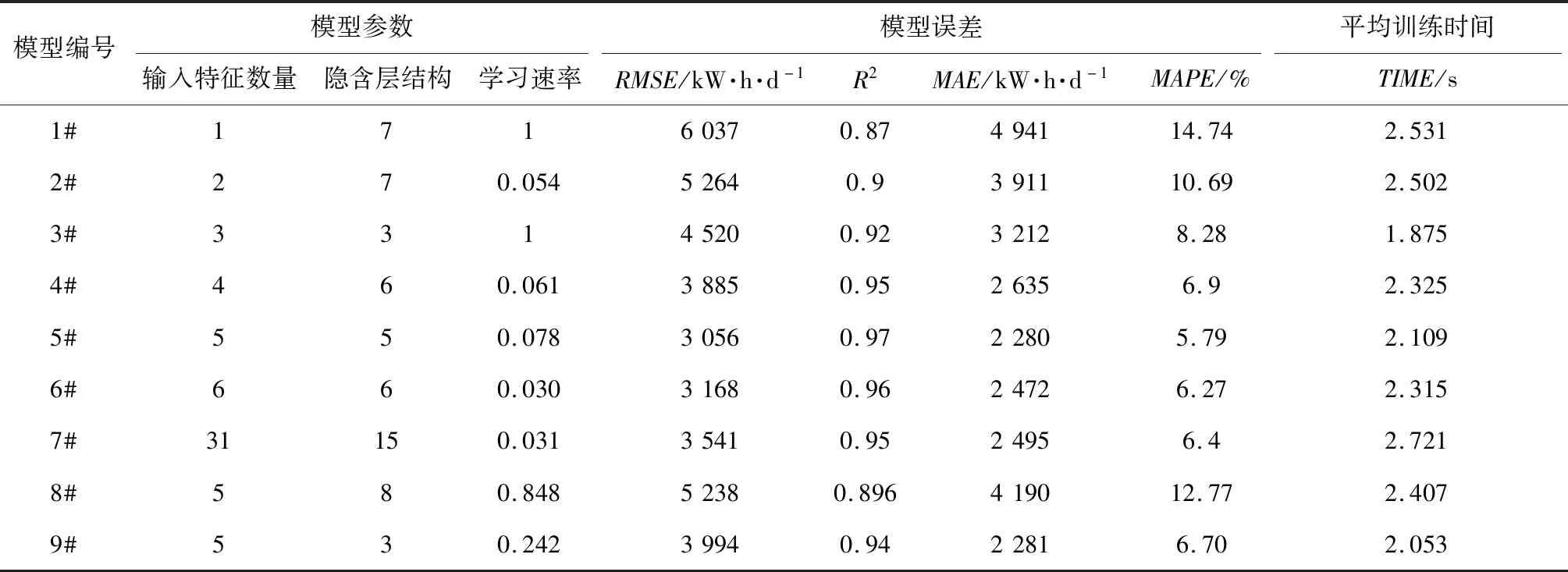
表4 模型参数、平均误差值与平均训练时间
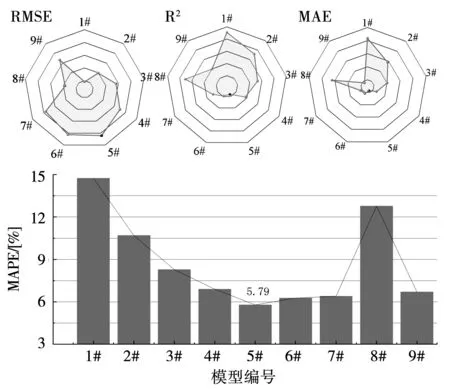
图5 模型误差分布图
分析1#~7#模型能够发现,模型预测误差随输入特征的增加呈现先降低后略微升高的特点,5#模型预测误差最小。说明利用K-EMI计算得到的5个特征已经包含了能够精确反映管道电耗变化的信息,其余特征多属于噪声特征,不利于提高模型预测效果。对比5#、8#和9#模型能够发现,提取5个特征时,通过K-EMI选出的特征能够建立更准确的电耗预测模型,这证明使用K-EMI计算该管线中不同特征与电耗相关性的效果优于使用互信息和皮尔逊系数计算的效果。7#模型比5#模型的隐含层神经元数量增加了10个,平均训练时间也增长了22.49%,这是由于输入特征数量增加,BP神经网络隐含层需要加入更多的神经元以学习不同特征间的规律,因此增加了模型训练时间。
5 结论
对比基于不同输入特征建立的神经网络预测模型的预测效果能够得到以下结论:
(1)在相关性分析前先利用相关公式对原始数据进行扩充能得到更多与电耗相关性强的特征。
(2)K-EMI能有效评价不同特征与电耗的相关性,且效果明显好于互信息和皮尔逊系数的效果。
(3)5#预测模型具有最高的预测精度和较短的模型训练时间,证明本研究提出方法建立的BPNN模型能够很好地预测管道电耗。

