基于密度峰值聚类的大学生异常行为检测研究
李慧芳 钟新成 付晓丽
(长治学院计算机系,山西 长治 046011)
1 引言
大学生健康安全成长是高等教育管理者所关注的重点工作。有些大学生因存在挂科、网贷、孤僻等异常行为成为学校的重点关注对象。如何及时发现学生群体中的学生异常行为并进行心理疏导和关怀,已成为高校学生心理健康管理工作的一项重要任务。
目前,常见的异常行为检测方法包括有监督的异常检测方法和无监督的异常检测方法。有监督的检测方法需要一个事先标记好的训练集,从而达到训练分类器识别异常数据的目的。对于异常用户特别稀少的情形,往往需要大量时间,寻找数据的效率较低。常采用支持向量机、神经网络等建立检测模型。无监督的检测方法不仅不需要提前标记训练集,在新的异常数据类型出现后,该方法能够更快更有效率地进行检测。常采用k-means、近邻传播等聚类方法对异常数据进行检测。这些算法通过对样本按照相似性分为若干簇,使得属于同一簇的样本之间的距离尽可能小而不同簇间的个体间的距离尽可能大[1]。
密度峰值聚类算法于2014年在《Science》上发表,受到了广大学者的关注[2-4]。目前,已有许多领域采用该算法检测异常数据特点问题。文献[5]通过优化初始聚类中心,采用密度峰值聚类检测算法改善电力大数据异常值的检测复杂度。文献[6]通过直方图均衡化原理优化类间距离,实现密度峰值聚类的短期光伏功率预测。文献[7]通过密度峰值聚类算法对未知链路进行分类,依据分类结果完成链路预测。文献[8]提出一种基于网格的密度峰值聚类方法,该算法的基本思想是采用双重网格划分方式对雷达信号脉冲进行实时聚类。实验结果表明,实时雷达分选聚类很好地处理了雷达信号的重叠严重问题。
本文将密度峰值聚类算法应用于大学生异常群体预测,首先采用加权欧式距离应用于样本点间距离优化,然后建立基于局部密度和高密度距离的决策图,最后识别正常样本点与异常样本点。
2 学生异常检测算法
2.1 密度峰值距离算法原理
密度峰值聚类算法属于一种可以发现非凸簇类的无监督学习算法,可以直观地找到簇数量,也很容易发现异常样本点。该算法的簇中心具有两个特点:1)样本点被相对密度较低的邻居样本点所包围;2)样本点与更高密度样本点对象具有相对较大的距离。
为了便于深入分析大学生群体行为,假设学生样本集X包括m个对象,每个数据对象有n个属性特征,则X={x1,x2,x3,…,xm},xi=(xi1,xi2,…,xin)。
对样本点xi的局部密度和高密度距离定义如下:(1)局部密度的定义:

其中i为第i个样本点,j为第j个样本点,dij为点xi和xj间的距离,参数d c为截断距离,φ(x)是分段函数,当dij (2)高密度距离的定义:大于自身局部密度的样本点中,与离自身最近的样本点之间的间距。对于任一点xi的高密度距离δi可表示为: 在密度峰值聚类中,距离度量方法会直接影响聚类算法的结果。常见的度量方法有欧式距离和马氏距离。欧式距离又称为欧几里得距离,可以通过样本之间的距离计算两个样本的相似度,距离越近就越相似[9]。在n维空间中,xi和xj间的欧式距离可表示为: 上述的欧式距离公式中样本点在每个位置的属性对样本集的影响认为是均等的,没有考虑样本各个维度之间的尺度不一致的问题,会导致判定结果产生误差。本文提出的属性加权距离度量方法直接作用到各个维度,将各个维度都满足标准正态分布。两个样本点的加权欧式距离表示为: 其中Sk表示第k维度的标准差。 (1)簇类中心的识别 簇类中心是同时具备较大局部密度和较大高密度距离的样本点,可表示为: 由簇类中心的定义可知,当样本点i成为聚类中心点时,其必然具有较大的密度ρ和距离δ,根据上述计算公式,此时样本点也应具有较大的γ值。该异常检测算法以局部密度ρ为横坐标距离δ为纵坐标进行绘制据决策图。图1为28个样本点的分布情况,图2为依据局部密度和高密度距离都大的样本点绘制的决策图。从图2可以看出样本点1和样本点具有较高的局部密度和高密度距离并可以选取为簇类中心。 (2)异常点的识别 为了识别异常点样本,将属于某一簇但是距离其他簇不超过d c的样本点的集合定义为边界区域,同时将边界区域中局部密度最高的点定义为ρb。簇中局部密度等于或小于ρb的样本点分离为异常点。 图1 样本点分布 图2 决策图 基于密度峰值距离算法的学生异常行为检测的步骤如下: 输入:高校学生数据样本集X={x1,x2,x3,…,xm} 过程: Step1:计算任意两样本点之间的距离d ij,构造相似度矩阵。 Step2:将矩阵前1%~2%的值作为截断距离dc。 Step3:根据公式计算数据样本集中各个对象的局部密度和高密度距离。 Step4:生成有关的决策图,标识具有高局部密度和高密度距离的点为簇类中心。 Step5:将非簇类中心分配到最近的高密度簇。 Step6:将局部密度不超过边界区密度的样本点视为异常点。 表1 月平均样本数据(部分) 表2 归一化后的月平均样本数据(部分) 输出:输出学生样本集的聚类簇以及学生异常点样本。 本文所用的验证数据集均为在长治学院智慧校园系统平台上采集,将13个系部30个班级共1500名大学生作为观察对象。采集数据分为消费数据、出勤数据、教学数据、娱乐数据、图书馆借阅数据五大类。消费数据包括学生食堂消费金额、网购快递次数。出勤数据包括学生运动出勤时间、公益活动时间、社团活动参与时间、食堂寝室时间、图书馆进出次数。教学数据包括课程作业完成情况、课堂参与度、早晚自习、课程成绩。网络娱乐数据包括网络游戏、网络追剧。图书借阅数据包括借阅次数、借阅书籍类型。 样本集的标准化对实验结果影响很大,因此在聚类前需要对样本点进行归一化处理,使得每个样本的属性值转换为[0,1]之间的数值。 样本数据如表1所示。 归一化处理后的样本数据如表2所示。 为了验证算法的性能和效果,本文采用未加权的欧式距离密度峰值聚类算法和加权欧式距离的密度峰值聚类算法进行比较,评价指标包括检测率和误检率。检测率用来表示被正确检测的异常学生个体占整个异常学生个体的比例。误检率用来表示正常学生个体被检测为异常学生个体数占整个正常学生个体数的比例。实验结果如表3所示。 表3 各算法聚类检测率和误检率比较 通过对有关班级辅导员和学生代表进行询问,实验结果筛选的部分学生异常个体符合对应学生的日常生活和学习行为。部分学生异常个体如表4所示。 表4 部分异常个体 从表3可以分析得出,19***201和19***203两位学生个体在校园活动记录较少,该生在图书馆进出次数、运动次数都较少、校园消费金额高、上网时间过长,该生可能存在不经常参加校园活动、作息不规律等行为,可将其认定为异常学生个体。该生辅导员有必要对其学习和生活状态进行了解,并与其适当进行交流和督促。 本文从高校校园大数据入手,采用密度峰值聚类算法设计并实现了异常学生个体的检测方法,并在聚类过程中选择特征加权的距离度量方法。通过实验证明,本文采用的检测算法能够获得较好的聚类效果和异常识别效果。本文的研究有助于高校管理者充分分析学生行为特点,而且能够更深层次地挖掘学生异常行为。在今后的工作中,会进一步研究学生属性之间的关联对聚类结果的影响。
2.2 特征加权的距离度量


2.3 簇类中心和异常点的识别

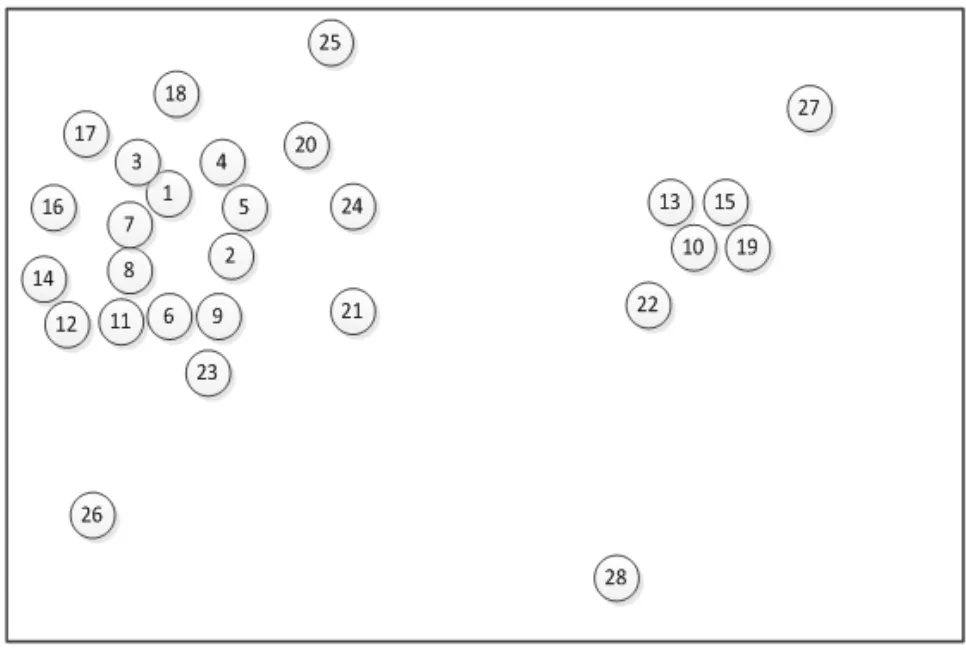
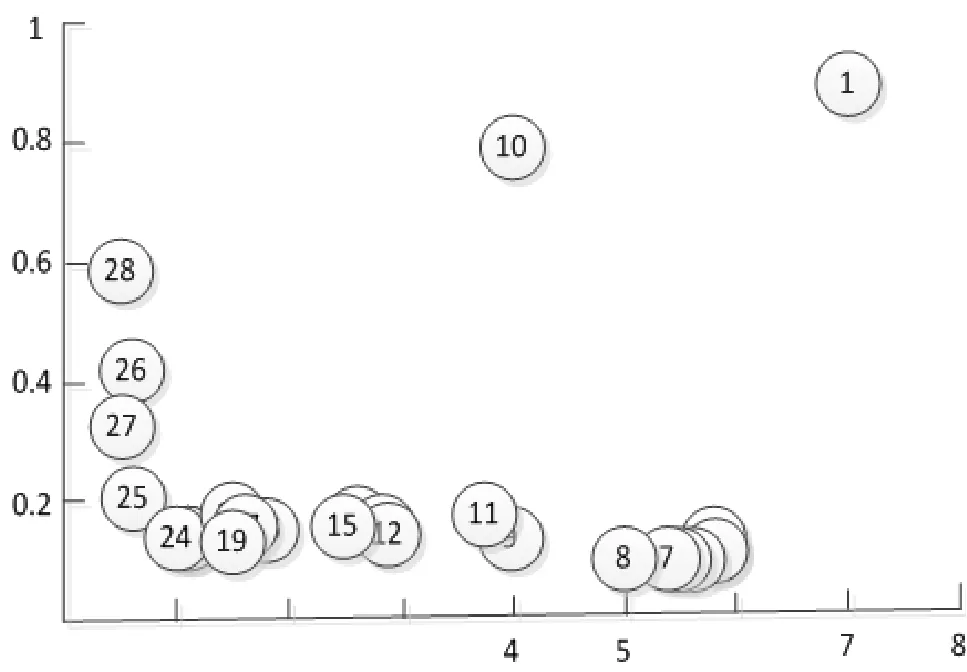
2.4 算法流程
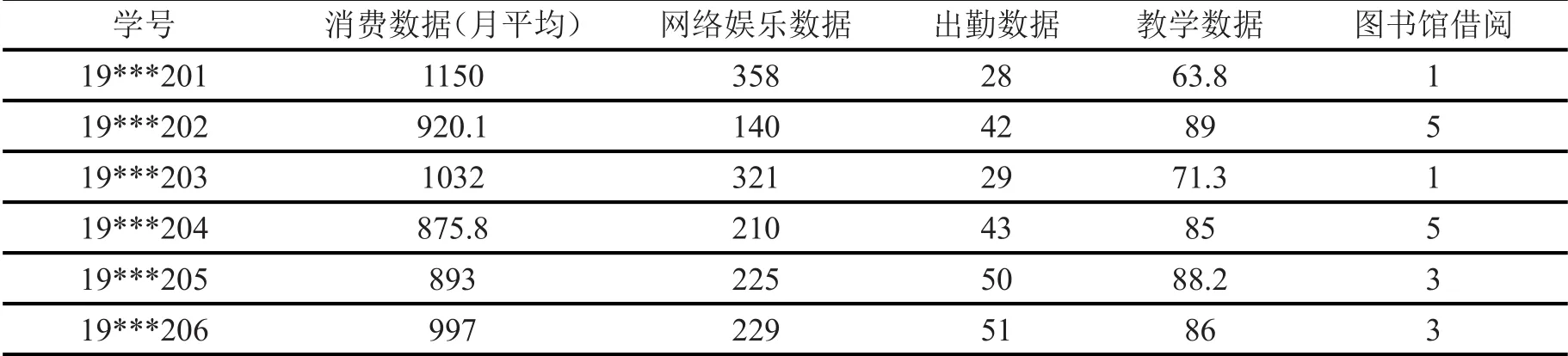
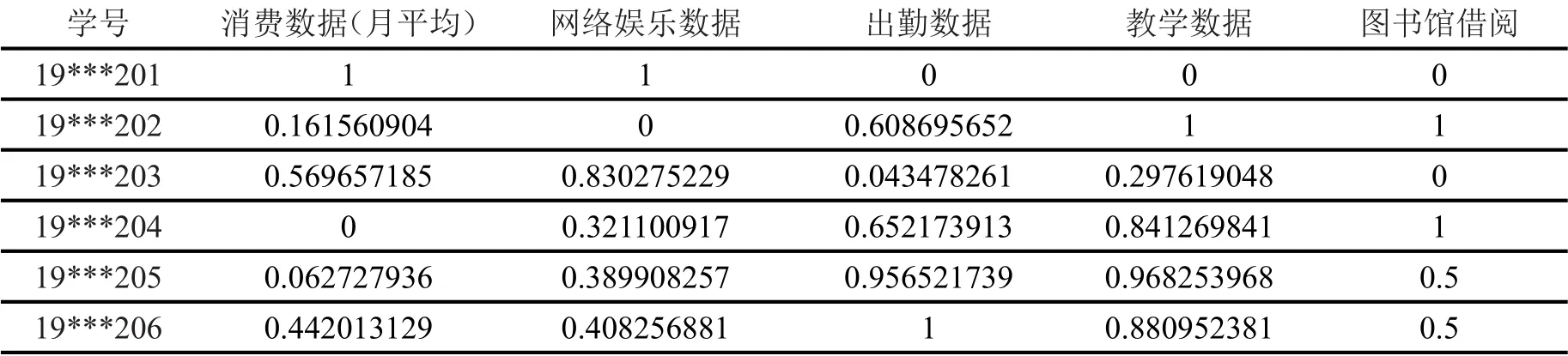
3 实验与分析
3.1 实验数据及预处理
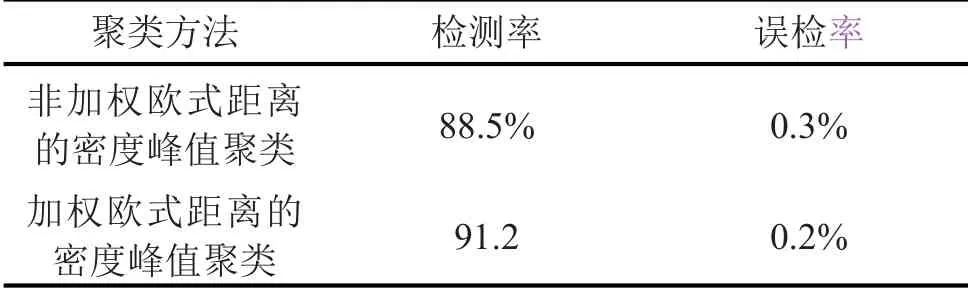
3.2 实验结果与分析

4 结语

