可撤销属性加密结合快速密度聚类算法的非结构化大数据安全存储方法
谷保平 马建红
1(郑州信息科技职业学院信息工程学院 河南 郑州 450046) 2(郑州大学软件学院 河南 郑州 450002)
0 引 言
多维大数据聚类期间的数据安全性是安全数据聚类的重要方面之一。通过编码方案进行不同类型的安全攻击,使用各种软件以及各种非法病毒和蠕虫是数据丢失的主要原因。因此,无论是从数据存储还是数据利用的角度来看,数据安全都是需要解决的问题。
国内外学者围绕非结构化大数据安全加密的问题展开了深入的研究。文献[1-2]利用k均值算法对大数据进行聚类,可以方便地挖掘有用信息,但由于算法可扩展性的限制,提出的有序聚类和期望最大方法不能直接用于大数据分类。文献[3]在文献[2]的基础上,使用无监督聚类法和模糊概率模型扩展了大数据聚类方法的应用,然而,当数据大小超过实际存储的大小时,所采用的算法在计算时间方面的扩展性很差,容易受硬件条件的限制。文献[4]提出通过自然语言处理对非结构化和结构化大数据进行情感分析,使用MapReduce技术处理非结构化数据,并通过协同过滤自动预测用户的品味,但该方法不能防止数据检索期间的数据丢失。文献[5]利用Trillion Particle Scale聚类技术扩展了新代码生成的最大数据集,有助于推断等离子体物理中粒子的加速,但其错误率较高,且作者没有提出任何有效的错误控制技术。为了减少数据开销以及多维大数据传输期间的安全开销,文献[6]采用BIRCH聚类算法对阈值进行自动估计,根据数据计算BIRCH的最佳阈值参数,使得大数据可以进行适当的聚类,但该方法依然牺牲了数据处理时间。文献[7]使用HDFS和MapReduce为Hadoop集群提出了一种内存利用技术,减少了Mappers的不同内存使用量以及Hadoop集群上数据存储和处理的减速器。然而,该技术不适用于复杂的时间序列数据,并且该算法的复杂性相对较高,这对于复杂的大数据应用来说并不完美。文献[8]用特征化和子集化技术来处理大数据工作负载,使用从PCA获得的主要模块来应用聚类技术进而研究大数据工作负载之间的相似性,提高了大数据处理的兼容性,但该技术不支持大量基准数据。除此之外,该技术不适合用于聚类它们的多维大数据文件。文献[9]提出了一个共同目标框架Petuum技术,通过感知机器学习程序,加速了迭代收敛的速度,可以分析大规模机器学习中的数据和模型。然而,就功能集而言,与Hadoop和Spark相比,Petuum技术仍然相对不发达。文献[10]采用SkeVa算法对数据进行k均值聚类,减少了大数据的维数和特征向量,但它不支持MapReduce框架,也不适合大数据文件的聚类,并且在聚类过程中可能会发生数据丢失[11]。
因此,为了减小非结构化大数据在组合聚类过程中的时间开销和防止大数据在传输过程中出现数据丢失以及安全攻击,提出了可撤销属性加密结合快速密度聚类算法的非结构化大数据安全存储方法,主要创新点总结如下:
(1) 本文算法采用输入非结构化文件,利用可撤销属性方法为非结构化大数据提供安全的存储结构,通过区分安全攻击和传输错误来防止大数据的误传和避免安全攻击,提高了数据传输和存储的安全性。
(2) 本文算法利用霍夫曼压缩技术对数据进行压缩,降低了数据传输、存储和聚类期间的开销。
(3) 由于传输错误、各种安全攻击、时间开销,以及空间开销而容易发生数据丢失现象,本文算法通过错误控制技术为潜在丢失的数据提供了备份系统,可有效防止数据丢失。
(4) 提出一种新的快速密度聚类技术,可有效处理多维大数据文件。
实验结果表明,相比于其他几种现有算法,本文算法在处理非结构化大数据问题方面具有更高的聚类效率、更低的开销和更好的兼容性。
1 方法设计
本文方法有四个部分。第一部分采用输入非结构化文件,如文本文件,利用可撤销属性方法为非结构化大数据进行加密,输入数据可以是任何类型,例如结构化[12]、非结构化或半结构化[13]。因此,这种大输入数据的类别也可能是不确定的。第二部分结合了霍夫曼压缩技术来控制实际数据以及该技术的安全开销,控制数据传输和存储或集群期间的数据错误。第三部分通过结合独特的错误控制技术作为集成技术,提供用于意外数据丢失的备份系统。第四部分中,在实施错误控制技术之后,应用了高效的快速密度聚类算法。本文方法执行过程如图1所示。
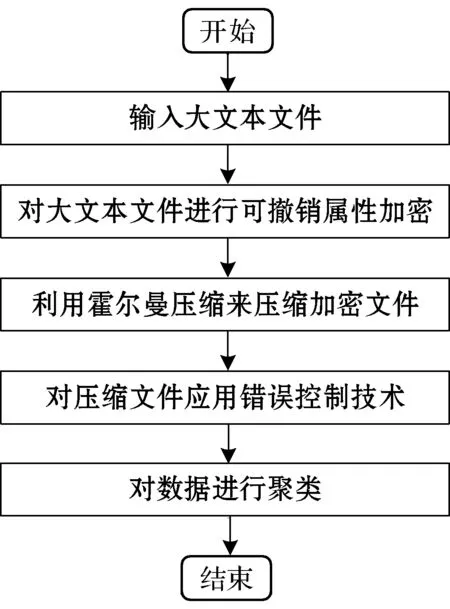
图1 本文方法执行过程
1.1 利用可撤销属性加密输入文本文件
根据可撤销属性加密技术的工作原理[14],输入数据大小为8位。 为了执行可撤销属性加密技术,每个单个字符取自输入文本文件,并在每次单次迭代期间通过其ASCII值转换为8位字符串。在遍历输入文本的所有字符后,从输入文本生成m个密文,并将其转换为4位密文[15]。从输入文本的每个原始字符生成每个4位密文CodeTextm,每个8位秘密密钥Mysm和相应的4位密码文本相互连接,通过式(1)生成12位加密字符串Strm。
(1)
将所有连接的加密字符串连接成单个隐含字符串Ste,最后进入的单个隐含字符串为:
Stem=Stem×(10)l(Strm)+Strm
(2)
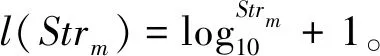
由于在加密期间添加了额外的位,增加了数据开销,因此,为了减少数据开销,将连接的单个隐含字符串Ste作为输入字符串来执行霍夫曼压缩[16]。
1.2 霍夫曼压缩
通过将输入的隐含字符串Ste分成多个8位字符串来启动压缩操作。然后将所有8位字符串转换为相应的ASCII字符并将它们存储在数组中。霍夫曼树通过以下算法进行创建。
算法1霍夫曼树
1.Ch←n个字符组;
//字符k的频率由F|k|定义
2.Seq←F的最小优先队列;
//Seq是一个列表,按频率升序排列
3.n=Ch;
//导入所有Ch到最小优先队列(Seq)
4.Seq=Ch;
5. 对于(i=1 ton-1);
//创建一个新节点z到n-1
6. 分配新节点z;
//z的左子结点是x,右子节点是y
//左子结点z是最不常见的弹出形式的ChSeq
7.left[z]=x=Extract_Min(Seq);
//从charSeq中弹出另外一个字符来创建新的右子节点
8.left[z]=y=Extract_Min(Seq);
//子节点的频率总和
9.F(z)=F(x)+F(y);
//将新创建的对象导入最小优先级队列
10. 导入(Seq,z);
11. 结束;
//返回到树的根源
12. 返回Extract_Min(Seq)
算法1中,步骤1和步骤2声明在制作霍夫曼树时所需的变量。步骤3至步骤4根据频率按升序创建非冗余排序字符列表,消除冗余字符。步骤5至步骤11收集每个字符的频率,并根据频率分布形成霍夫曼树。根据频率,霍夫曼树的左右子集已被决定并放置在新生成的霍夫曼树中。步骤12重复相同的过程以完成所需的霍夫曼树的形成。在创建压缩代码之后,遍历了完整的字符列表Ch,并且所有相应的字符已被压缩的代码替换。之后,压缩代码在式(2)的帮助下连接成单个字符串Temp。以同样的方式,将频率表作为字符串Sta和短路字符表在式(2)的帮助下连接成字符串Ch′。然后,通过为每个分隔符连接100位二进制分隔符来创建一对分隔符Fen和Fen′。在下一步中,将Temp、Ch′、Fen和Fen′连接成单个最终压缩字符串CStr。通过在最终压缩字符串CStr中添加压缩代码字符串Sta来初始化连接操作,如下:
CStr=CStr×(10)l(Temp)+Temp
(3)

在第二阶段,第一个分隔符Fen已添加最终压缩字符串CStr,如下:
CStr=CStr×(10)l(Fen)+Fen
(4)

在将第一个分隔符Fen与最终压缩字符串CStr连接后,频率字符串Fen已被添加,如下:
CStr=CStr×(10)l(Fen)+Fen
(5)

在添加完频率字符串Fen后,第二个分隔符Fen′添加了最终压缩字符串CStr:
CStr=CStr×(10)l(Fen′)+Fen′
(6)
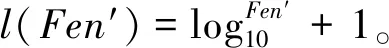
最后的连接字符串Char′在最后阶段添加了最终压缩字符串CStr以获得竞争压缩字符串:
CStr=CStr×(10)l(Ch′)+Ch′
(7)
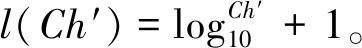
这里添加两个分隔符Fen和Fen′的目的是在最终压缩字符串CStr中的压缩代码Temp、字符和频率字符串之间建立空格。基于这两个分隔符,压缩代码、字符和频率字符串将在解压缩操作期间分离。
1.3 错误控制技术
将最终的压缩字符串作为输入,并将其分成8位字符串,以执行建议的错误控制位生成以及合并操作。 所有新分离的8位字符串都存储在字符串数组Ec中,并按照算法2进行操作。
算法2错误控制位生成和合并技术
1. 设置Ec中的元素总数量为n;
2.m1、n1、k1为整型变量,并且k1=0;
3. 声明Ec′为字符数列,Xs为字符变量;
4. 运行每两个Ec元素之间的异或操作并将它们以及最终错误控制数列Ec′中生成的Xr用字符串Xs储存起来;
5. 当(intm1=0;m=m+2)时
Xs=″″;
Ec′[k1]=Ec[m1]
Ec′[k1+1]=Ec[k1+1]
6. 当(intn1=0;n1=m1+1)时
Xs=Ec[n1][m1]⊕Ec[m1+1][n1]
Ec′[k1+2]=Xs
7. 结束。
算法2中,步骤1到步骤3声明变量、数组并初始化整数变量p。 因此,步骤4和步骤5在字符串数组Ec的每个双连续元素之间执行Xr运算,并将得到的Xr字符串存储在字符串变量Xs上。同时,步骤5将每两个连续元素存储到最终的错误控制数组Ec′上。步骤6在连接每个双输入字符串后,将每个结果Xr用字符串Xs存储在字符串数组Ec的第三位,且每个双输入字符串取自字符串数组Ec。所提出的错误控制技术可以解决每个单独的比特。在任何情况下,如果任何比特被破坏,则可以通过相应比特之间的Xr操作来检索该比特,取自其他两个串,即得到的Xr串和第二个原始串。除此之外,如果任何原始字符串在任何意外情况下完全损坏或丢失,则可以通过在第二个原始字符串和结果Xr字符串之间执行Xr操作来检索整个字符串。此后,所提出的错误控制技术也可以为意外数据丢失提供备份系统。
1.4 快速聚类算法
本文提出一种快速聚类算法,用于处理和存储加密数据。在检索加密数据时,已经应用了低复杂搜索算法。通过算法3更精确地显示所提出的多维聚类技术。
算法3快速聚类算法
输入:聚类数量Num,数据集Ser,数据对象Opt,属性集Att;Ser={Ser1,Ser2,…,Serm};Att={Att1,Att2,…,Attm};其中0≤Num,Opt<∞并且Num≤Opt。
输出:一组聚类N。
1. 从原始数据组(Ser)中绘制多个子样本(Ser1,Ser2,…,Serm);
2. 将每一组的中间点作为形心;
3. 计算每一组数据点和所有起始形心之间的距离;
4. 找到距离形心最近的点并且将其纳入最近的聚类;
5. 选择从聚类到形心的最小距离;
6. 将步骤1到步骤5应用到聚类Num的数据组;
7. 将两个聚类合并为一个聚类;
8. 重新计算组合聚类的新的聚类中心直到聚类的数量缩减到Num。
算法3展示了所提出的快速聚类算法,并展示出了如何利用该算法处理输入数据。使用连接的搜索关键字搜索加密文本[17],如果搜索失败,则混合搜索技术需要申请搜索。在该预先搜索方法中,使用可撤销属性加密技术将搜索技术的关键值转换为隐藏文本,然后执行搜索。因此,所提出的快速密度聚类技术可以执行不确定和非结构化以及多维大数据文件。
2 实 验
2.1 实验配置
进行实验的硬件配置包括:英特尔酷睿i5处理器、4 GB DDR3内存和2 TB大小的HDD;软件包括:Ubuntu 12.4 LTS作为操作系统,核心JAVA作为编程语言。将纯文本(.txt)文件作为输入数据,将.WAV文件作为输入音频文件,生成stego音频文件。输入文件大小可能在50 GB到1 TB之间。所有实验都是在无线环境中进行的。
2.2 实验参数
2.2.1信息丢失(IL)
在群集和存储期间,某些部分信息可能被修改或损坏或丢失。大多数情况下,这些信息无法在接收端检索,即永久丢失,这种现象被称为信息丢失。任何传输系统产生数据完整性的能力可以通过计算信息丢失的总量来测量。除了数据完整性之外,它还确保了对各种数据错误的稳定性。信息丢失被公式化如下[18]:
(8)
通常在数据检索期间,永久损坏或不可恢复的信息会被丢弃[19]。因此,如果在数据检索期间发生信息丢失,则检索到的文件大小必须小于原始文件。这就是为什么通过找到原始文件和检索到的文件大小的差异来测量信息丢失的原因。因此,IL对于计算聚类过程中的数据丢失非常重要[20]。
2.2.2信噪比
信噪比是所需模拟或数字数据样本相对于背景噪声的幅度或长度方面的强度[21]。它主要是为了显示产生对各种声道噪声的稳定性的能力。任何误差控制技术产生的信噪比(Signal Noise Ratio,SNR)都可以用分贝(dB)对数表示,并表示为:
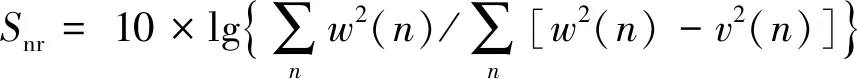
(9)
式中:w(n)是原始输入样本长度;v(n)是输出样本文件的样本长度。本文技术结合了独特的错误检查技术,以增强数据的稳定性和机密性。如果样本的Snr高,那么可以说样本错误较少,如果任何样本的Snr都很低,那么它就说明样本是高度错误的。
2.2.3压缩比
数据压缩比,也称为压缩功率,用于量化数据压缩算法产生的数据表示大小的减少。数据压缩比类似于用于测量物质的物理压缩的物理压缩比。任何压缩技术的压缩比可以计算为:
(10)
通常,压缩比表示减小任何压缩技术的文件大小的能力。因此,如果任何压缩技术产生高Cdr,那么该压缩技术不能有效地减小输入文件大小,反之亦然。
2.2.4通量
通常在计算系统中,每项工作都需要在指定的时间内完成。完成此类工作的时间要求随计算系统的处理速度和工作的性质而变化。与数据传输系统相同,时间是一个重要因素; 整个数据需要在指定的时间内传输。因此,需要在时间上测量任何计算系统或传输系统的性能。通量是指在给定时间内完成的工作量,反映了某种技术的时间效率。任何技术产生的通量可以计算为:
(11)
通量是衡量任何安全数据传输系统的时间效率的重要参数。通量与文件大小成正比,与处理速度成反比。因此,如果任何计算系统在执行某项工作期间产生高吞吐量,则表示该工作具有较高的时间效率,反之亦然。
2.2.5环路复杂度
任何技术的时间复杂度决定了它的时间效率。 如果任何技术的时间复杂度很高,则说明它的时间效率很低,反之亦然。在确定任何技术或算法的时间复杂度的各种方法中,环路复杂度的计算是其中之一。环路复杂度是源代码复杂度测量,其与许多编码错误相关联。它是通过开发代码的控制流图来计算的,该代码的测量是通过程序模块的线性无关路径的数量。 任何技术或算法的环路复杂度Cplx可以确定为:
Cplx=(Length-Node+(2×Pnum))
(12)
式中:Length表示控制流图的各种边;Node是节点数;Pnum是图的连通分量数。本文的集成模型的时间复杂度是通过计算其环路复杂度来得到的。如果任何技术的环路复杂度很高,则认为它是高度时间复杂的,反之亦然。通常,环路复杂度随着环路复杂度的不同技术范围而变化,表1对比了不同环路复杂度下的特性。

表1 环路复杂度的特性
2.3 实验结果
2.3.1信息丢失的效率
通过测量导入文件产生的信噪比和信息损失百分比,可以确定由于各种类型的错误以及安全攻击而在聚类期间保护信息丢失的本文方法的性能。如果任何安全系统产生更高的信噪比值,则所使用的安全系统被认为对数据错误和各种安全攻击具有稳定性。同时,如果任何安全系统提供较低百分比的信息丢失,则所使用的安全技术被认为有效地增强了数据完整性。此后,由集成技术提供的信息损失百分比和信噪比如图2和图3所示。
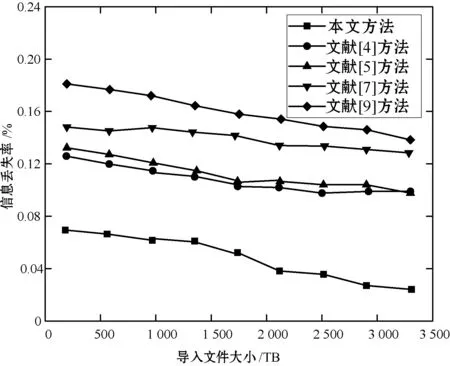
图2 本文提出的合成技术的信息损失百分比
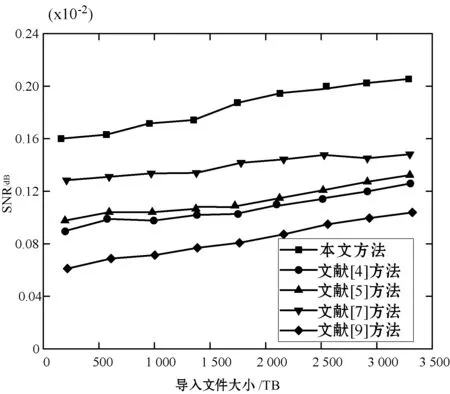
图3 本文提出的错误控制技术的信噪比
实验中默认数据大小变化范围为100 TB到3 400 TB,将集成技术的性能与文献[4-5,7,9]中的各种现有的聚类技术进行了比较,结果表明本文提出的聚类技术能明显降低信息丢失的百分比。
如图2所示,文献[9]方法无论在小尺寸文件还是较大尺寸文件下都具有较高的信息丢失率,文献[4-5,7]中的聚类技术对信息损失百分比控制大体相近,但都随着数据包尺寸的增大而减小,而相对于本文方法仍然具有较高的信息丢失率;因此,从结果可以得出结论,与文献[4-5,7,9]中的聚类技术相比,本文方法通过保护各种数据错误和安全攻击来保护聚类期间的信息丢失更加有效。
此外误控制技术的性能可以通过其控制各种数据错误的能力来检查,这些数据错误是由不同硬件和软件限制以及通过计算信噪比而导致的各种安全攻击所引起的,因此对本文方法在误差控制过程中的信噪比与文献[4-5,7,9]中的误差控制技术进行了比较,结果如图3所示。
在不同导入文件尺寸下,不同方法有着不同的信噪比,但所有方法的信噪比都随着导入文件的增大而增加;其中:文献[9]方法信噪比始终保持最小,文献[4]和文献[5]方法信噪比相近,但较文献[7]低,本文方法则具有最高信噪比。因此可以看出,本文提出的差错控制技术比文献[4-5,7,9]中的误差错控制技术具有更高的信噪比,即本文提出的错误控制技术比现有错误控制技术更有效,并且在由于各种硬件、软件、其他明显的限制和安全攻击而引起的错误控制过程中,本文方法具有更高的保护各种数据错误的能力。
综合图2和图3所示结果,本文方法在聚类过程中相比于文献[4-5,7,9]中的相关技术具有更高的数据保护效率。
2.3.2数据和安全开销的效率
在表2中,将提出的霍夫曼压缩技术的性能与文献[4-5,7,9]中的压缩技术的性能进行了比较。这些压缩技术的比较是根据它们产生压缩比的能力来完成的。可以看出,提出的霍夫曼压缩技术提供了比文献[4-5,7,9]中的压缩技术更高的压缩比。根据定义,如果使用的压缩技术提供更高的压缩比,则称压缩技术对于压缩数据是有效的。由于霍夫曼压缩与文献[4-5,7,9]中的压缩技术相比,能够产生更高的压缩比,因此提出的压缩技术能够明显地、有效地减少数据以及安全开销。

表2 各种压缩技术的压缩比
2.3.3时间开销的效率
表3比较了本文方法的执行速度与文献[4-5,7,9]中的聚类技术在聚类和数据检索期间的通量。可以看出,本文方法聚类速度通量和数据检索通量分别为5.56和5.71,即相比于文献[4-5,7,9]中的聚类技术有更好的时间性能。
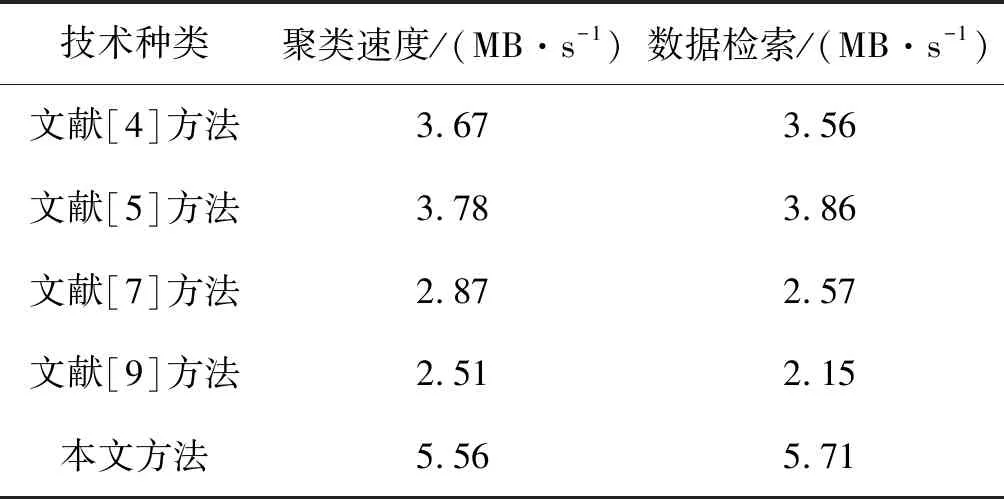
表3 聚类技术的通量
表4给出了聚类和数据检索时间期间的环路复杂度,可以看出,在聚类和数据检索时间的两种情况下,本文方法比文献[4-5,7,9]中的聚类技术具有更低的环路复杂度,分别为3和3,而文献[5]和文献[9]方法环路复杂度最高,文献[4]文献[7]则具有相同的聚类和检索复杂度,分别为4和3。因此可以得出结论,提出的集成聚类技术比文献[4-5,7,9]中的聚类技术具有更好的时间效率。
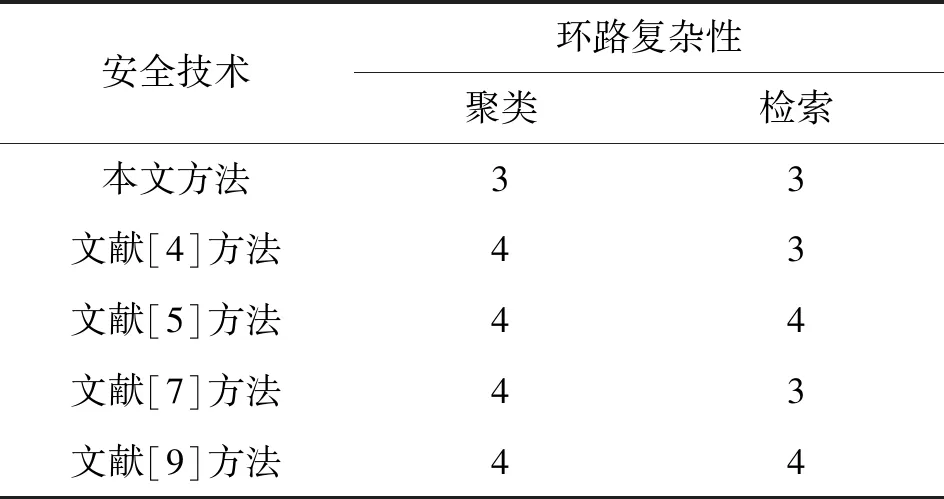
表4 不同技术的环路复杂性
3 结 语
本文提出一种可撤销属性加密结合快速密度聚类算法的非结构化大数据安全存储方法,研究了多维大数据快速分类和有效避免遭受安全攻击的问题。本文算法提高了数据的处理速度和安全加密的可靠性,降低了信息损失百分比,提高了压缩比和信噪比。
后期研究重点包括两点:1) 通过研究寻找可用于多维大数据聚类的集成安全机制,进一步提高大数据聚类的速度;2) 将组合的集成技术用于保护数据免受各种安全攻击的大数据加密技术,进一步减少数据和安全开销的压缩技术。

