基于改进的BiasSVD和聚类用户最近邻的协同过滤混合推荐算法

刘 超 赵文静 贾毓臻 蔡冠宇

1(江苏大学电气信息工程学院 江苏 镇江 212013) 2(镇江市丹徒区科学技术局 江苏 镇江 212000)

0 引 言

随着互联网的快速发展，交互式网络电视(Internet Protocol Television, IPTV)已成为电视业务中不可或缺的一部分。但是IPTV所提供的视频资源数量庞大，如何帮助用户从海量数据中快速获取感兴趣的内容是运营商现阶段迫切需要解决的问题。虽然关键字搜索可以一定程度上缓解信息过载问题，却不能满足用户的个性化需求。亚马逊表示35%的销售额来自推荐系统；谷歌新闻称推荐系统使其文章阅读量提高了38%[1]。

推荐系统可以根据家庭用户的收视行为和流量特征，分析用户的收视偏好，挖掘出用户的潜在个性化需求，进一步提高用户收视质量，为用户提供高效、快速、优质的个性化推荐服务。但是用户行为数据十分庞大并且每时每刻都在倍增，如何迅速定位用户偏好，保证推荐时效性，亟待研究。

如今主流的推荐系统主要采用混合推荐方案。混合推荐能够针对不同的实际情况，综合各推荐系统的优缺点，将多种推荐方案进行有效结合。刘雨薇[2]提出了一种改进的基于用户聚类的协同过滤算法，先将用户根据OCEAN模型进行聚类，然后用基于BiasSVD的协同过滤方法在用户所属类簇内对用户进行协同过滤。郑丹等[3]提出了一种用户聚类推荐算法，主要通过Weighted-Slope One来缓解数据稀疏性以及实时性差的问题。陈清浩[4]在SVD算法衍生的隐语义模型中，利用梯度下降法缓解了SVD算法中的可扩展性问题。

在个性化推荐系统中，对每个用户最近邻的查找都是基于大规模的用户空间，而且当出现新用户或者新物品时，传统协同过滤推荐算法(Collaborative Filtering,CF)的计算量将会倍增，系统的时效性无法得到保证，推荐物品的可靠性和有效性降低。

本文针对IPTV业务的多样性和复杂性问题，根据用户收视偏好，提出基于改进的BiasSVD和聚类用户最近邻的协同过滤混合推荐算法，有效缓解用户评分矩阵可扩展性问题，获得更加精确的用户预测评分，为用户提供精准快速的针对性推荐服务。混合推荐算法基本框架流程如图1所示。

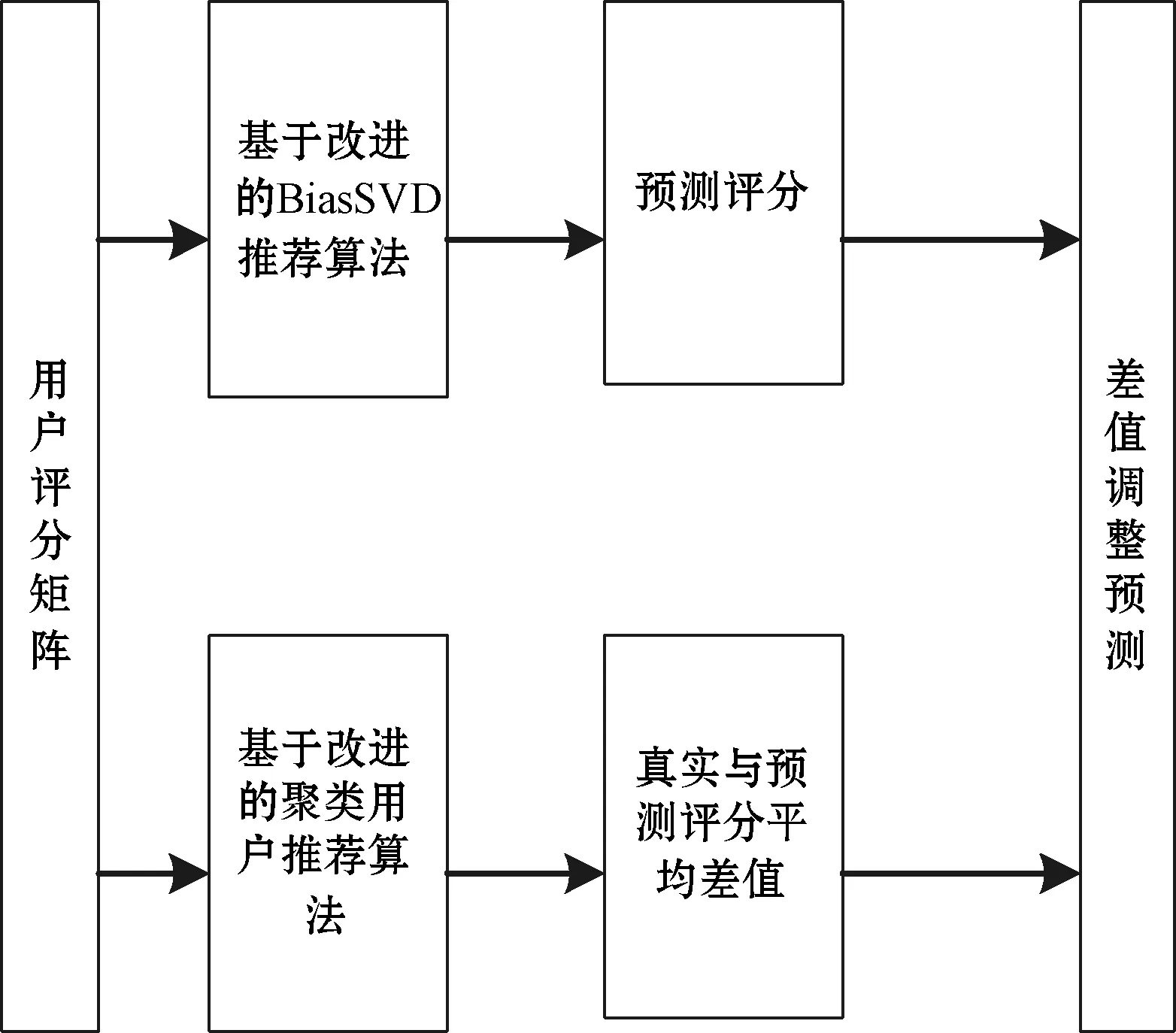
图1 混合推荐算法流程

1 改进的BiasSVD协同过滤推荐算法

1.1 BiasSVD

目前应用比较广泛的矩阵分解方法有奇异值矩阵(SVD)分解[5]、FunkSVD分解[6]和BiasSVD分解[7]。

SVD分解的基本原理是将m×n阶的矩阵A分解为U、S和V三个低秩矩阵，表示为:

Am×n=U×S×VT

(1)

奇异值具备衰减速度快的特性，一般情况下前10%甚至1%的奇异值之和就占据所有奇异值之和的99%以上[8]，所以选取前k个奇异值所构成的对角矩阵Sk与其对应的左右奇异向量来近似表示矩阵：

(2)

SVD算法通过选用元素值较大部分的奇异值来降维并进行奇异值分解，该算法存在的不足主要体现在两个方面。其一，SVD分解要求矩阵不能是稀疏的，即矩阵的所有元素不能有空值，有空值时A不能直接进行SVD分解，而大多数情况下评分矩阵都是十分稀疏的，稀疏度在90%以上。其二，SVD算法的计算繁琐，并且在高阶且密集的矩阵上运算，将大大降低系统运行效率。对此，2006年Funk提出FunkSVD算法，下面对该算法做简要介绍。

Am×n=PTQ

(3)

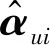
(4)

FunkSVD相对于传统的奇异值分解进行了优化，但该方法得到的预测评分依然存在一定程度误差，下面将其改进得到BiasSVD。

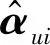
(5)

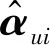
(6)

从而计算出误差平方和：

(7)

根据梯度下降算法，令更新步长为γ，得到递推公式，表示为:

(8)

1.2 改进的BiasSVD算法

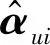
(9)

式中：用户u已完成评分的项目集合为Iu，浏览过但是未进行评分的项目集合为Nu;u对项目j(j∈Iu)的实际评分为αuj;xj是用户u已完成评分的项目属性;yj是没有评过分的项目属性。则误差以及误差平方和分别表示为:

(10)

(11)

则S在变量xj、yj、bu、bi和qi处的梯度分别表示为：

(12)

根据梯度下降算法，则推导出递推计算式为：

bu-bj)]-λxj)

bu→bu+γ(eui-λbu)

bi→bi+γ(eui-λbi)

(13)

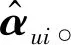
改进的BiasSVD算法虽然在预测过程利用视频属性来表示用户属性，降低存储空间，但是预测精度上还是会有一定的偏差存在，因此通过找到目标用户的最近邻用户，并计算其对视频的预测评分以及真实评分之间的平均差值，从而调整目标用户的预测评分。改进的BiasSVD算法预测用户评分流程如下：

(1) 输入训练数据，包括商品分类标签、关注度。初始化偏移向量bu、bi、隐因子矩阵qi，计算评分平均值μ。

(2) 初始化用户的隐式反馈数据x、y。

(3) 按照改进BiasSVD公式预测用户在此类视频的关注度。

(4) 计算误差值，按照改进BiasSVD公式迭代求解x、y、bu、bi、qi。

(5) 判断是否存在下一条关注度记录，存在则转至步骤(3)，否则转至步骤(7)。

(6) 判断是否存在下一个用户，如果存在则转至步骤(2)，否则转至步骤(7)。

(7) 判断是否存在下一轮迭代，如果存在则转至步骤(2)，否则输出关注度预测矩阵，算法结束。

2 改进的聚类用户最近邻协同过滤推荐算法

2.1 k-means聚类

k-means聚类[9]过程的核心思想如下：首先在全部对象中任选k个作为聚类中心；然后通过用户相似度sim(u,v)计算出用户与每个聚类中心的相似度，并且将用户分至所得值最大的簇内，直至全部划分为止，得到k个簇群；再更新聚类中心并重复上述步骤，直到每个聚类中心在每次更新后几乎不变为止；经过迭代得到最终的k个聚类簇群。

依据以上步骤后得到的各簇内，各用户之间都拥有极大的相似度。聚类结束后，再根据公式计算出目标用户和各聚类中心相似程度，目标用户的邻居集合就是相似度最高的簇中用户集合。得到目标用户与邻居集合中用户的相似度值，并且按照从大到小的顺序排列，取得的前N个用户即为最近邻集合。

本文将选择采用Pearson相关系数代表用户相似度：

(14)

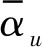
然而传统的CF算法没有将用户兴趣变化因素考虑其中。用户对某类视频的兴趣热度对用户的行为有很大影响，综合考虑该影响因素，将会很大程度提高推荐系统的预测准确度。

2.2 兴趣热度因子

用户对某类视频的兴趣热度会随着一些外在或内在因素而产生改变，这就会很大地影响系统的后期预测。依据艾兵浩斯遗忘曲线[10]，关注某类视频时的时间戳t与用户的相关性函数定义为：

f(t)=1-μ(T-t)λT≥t

(15)

式中：μ和λ表示兴趣热度衰减因子;T表示当前时间。所以当t=T时，f(t)达到最大，表示此时用户兴趣热度最大。

2.3 改进的聚类用户最近邻

本节在传统k-means聚类算法的基础上，引入权值函数f(t)，则式(14)可以优化为：

(16)

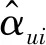
(17)

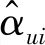
(1) 随机选择k个用户作为聚类中心，按照式(16)得到用户与k个中心的相似度，将该用户划分到相似度最高的簇中，经过不断迭代聚类中心，最终所有用户被分别归类进k个簇中。

(2) 找到目标用户所在的簇。

(3) 基于式(16)计算出目标用户与其他用户之间的相似度，将所有用户中相似度最高的N个用户指定为目标用户最近邻。

(4) 按照式(17)得出目标用户对项目的预测评分。

(5) 向目标用户提供TopN推荐。

3 混合推荐算法

本文综合改进的BiasSVD和改进的聚类用户最近邻两种算法，提出一种基于改进的BiasSVD和聚类用户最近邻的协同过滤混合算法。该混合算法的具体步骤如下：

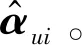
(2) 根据改进的聚类算法流程中步骤(1)-步骤(3)确定目标用户的最近邻用户user(u)。

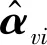
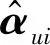
上述混合推荐算法中偏差调整的计算式为：

(18)

(19)

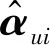
4 实 验

4.1 实验环境和数据集

实验环境：MATLAB R2016a，Windows 10 64位专业版，AMD A10-7890K Radeon R7。

数据集：为使得研究具有更高的参考价值，实验采用由明尼苏达大学收集的标准数据集作为数据输入。该标准数据集取自MovieLens影评网站中近千名用户针对1 682部电影的100 000次评分记录，且每次评论后网站都会对用户与项目的ID账号、时间戳、用户对项目的评分四个属性进行保存，其中评分范围是介于1～5之间的整数，分值的高低代表用户对电影的爱好程度，分值越高表示用户对此类视频的兴趣度越高[11]。测试集和训练集的比值为2 ∶8。

在上述数据集基础上可对用户项目的评分矩阵稀疏度进行计算，具体如下：

可以看出该数据集稀疏度为93.70%，高于90%，由此可以得出该评分矩阵为稀疏矩阵。

4.2 实验评价标准

本文采用平均绝对误差(MAE)方法来验证所提出的混合算法的准确性与有效性，该方法主要评估预测评分和实际评分间的差异[12]。假设目标用户对N个项目进行预测评分，MAE计算式为：

(20)

式中：pi为预测评分;ri为实际评分。由式(20)可知MAE值越小，说明推荐的项目越贴近用户需求，同时表明该推荐算法性能越优。

4.3 实验结果

本文通过实验1至实验3来验证混合算法的性能。实验设置更新步长为0.95，即γ=0.95，迭代次数step=100，正则化参数λ=0.3。

实验1：改进的混合推荐算法在不同特征矩阵维度下不同近邻数k的MAE值比较。本实验主要研究不同特征维度下的不同最近邻居数对本文算法预测准确性的影响。实验设置特征矩阵维度初始值为10，且每次增加的步长为10，直至矩阵维度达到50截止，选择的近邻数依次是k=10、k=20和k=30，实验结果如图2所示。

图2 特征矩阵维度与近邻数的关系

随着k值的增加且特征矩阵维度不变的情况下，本文算法的MAE值减小，算法预测准确度提高。随着矩阵维度的增加且k值不变的情况下，MAE值先降低，当矩阵维度扩大到一定范围时，MAE没有继续下降，因为随着矩阵维度的增加，该算法计算量增大，有效性有所降低。本次实验结果表明，当矩阵维度为30时，并且k取30，MAE值最小，推荐质量最好。

实验2：不同算法在不同特征矩阵维度下MAE值比较。本实验主要是将BiasSVD算法和本文所提改进混合推荐算法进行不同矩阵维度下的MAE对比。基于实验1，取k=30作为本文算法的目标用户的最近邻数，特征矩阵维度取值范围从10到50，每次增加10。结果如图3所示。

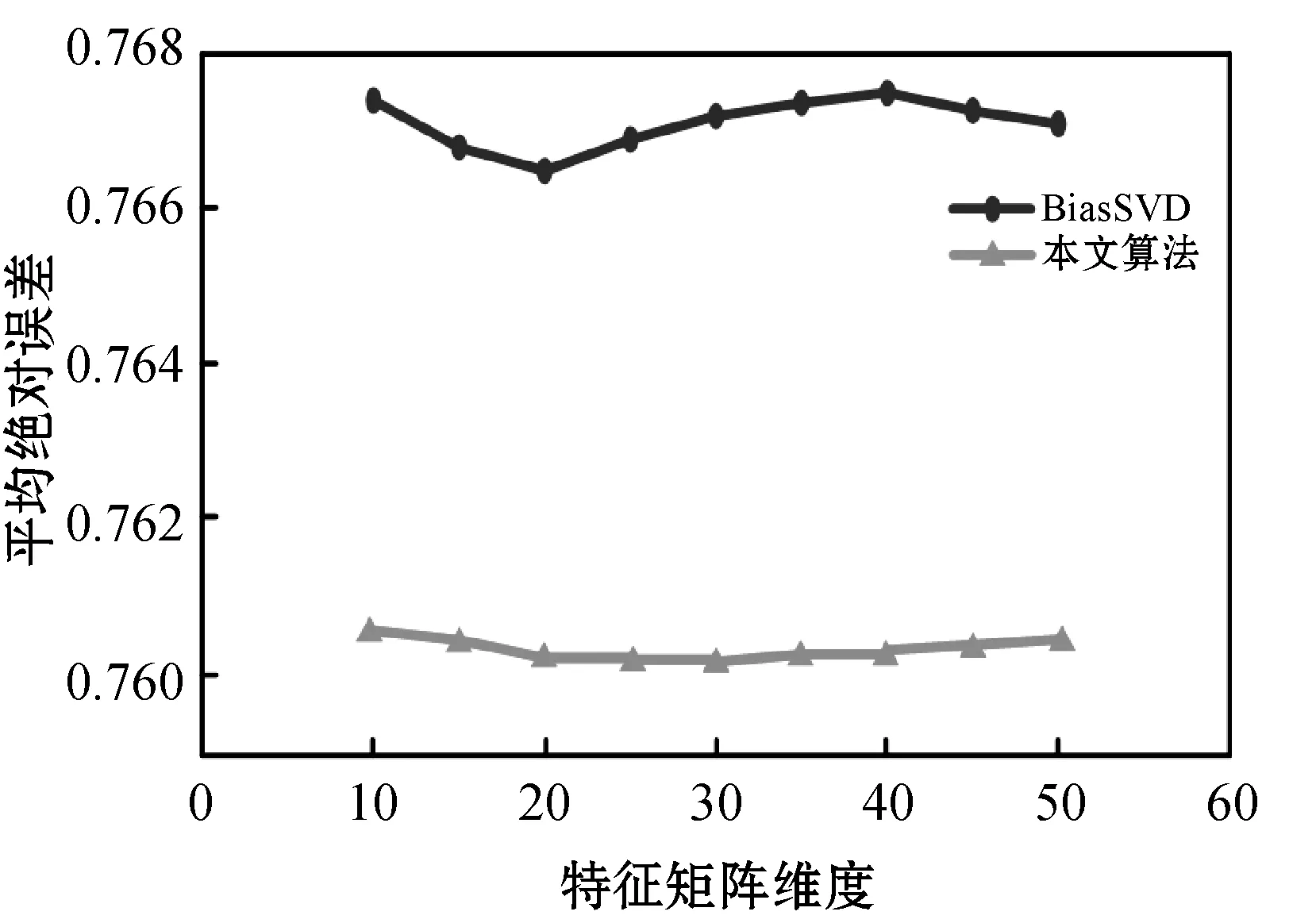
图3 不同算法在不同矩阵维度下MAE值比较

当混合推荐算法的最邻近k取30时，在不同的矩阵维度下，BiasSVD算法的MAE值均高于本文算法，可见本文算法能够缓解矩阵可扩展性问题。

实验3：不同算法在不同近邻数k下MAE值比较。本实验主要是将传统的CF算法与本文算法进行不同近邻数k下的MAE值对比。基于实验1，取30作为本文算法的特征矩阵维度，采样密度为原数据的90%，k取值范围从5到35，每次增加5，则实验结果如图4所示。

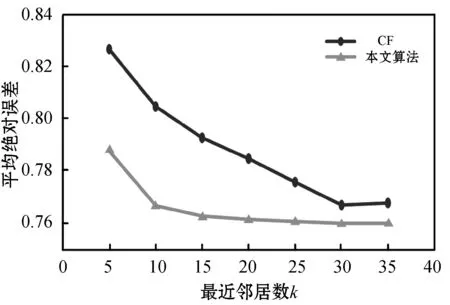
图4 不同算法在不同近邻数k下MAE值比较

可以看出，当特征矩阵的维度为30时，相比于传统的CF算法，改进的混合推荐算法拥有更小的MAE值。实验表明，本文算法的准确度得到较好的改善。

实验4：不同混合推荐算法在相同稀疏度下的MAE值比较。本实验将本文算法与基于SVD和用户聚类的协同过滤算法研究[11]中的混合推荐算法进行对比。采样密度为原数据的80%，实验结果如图5所示。

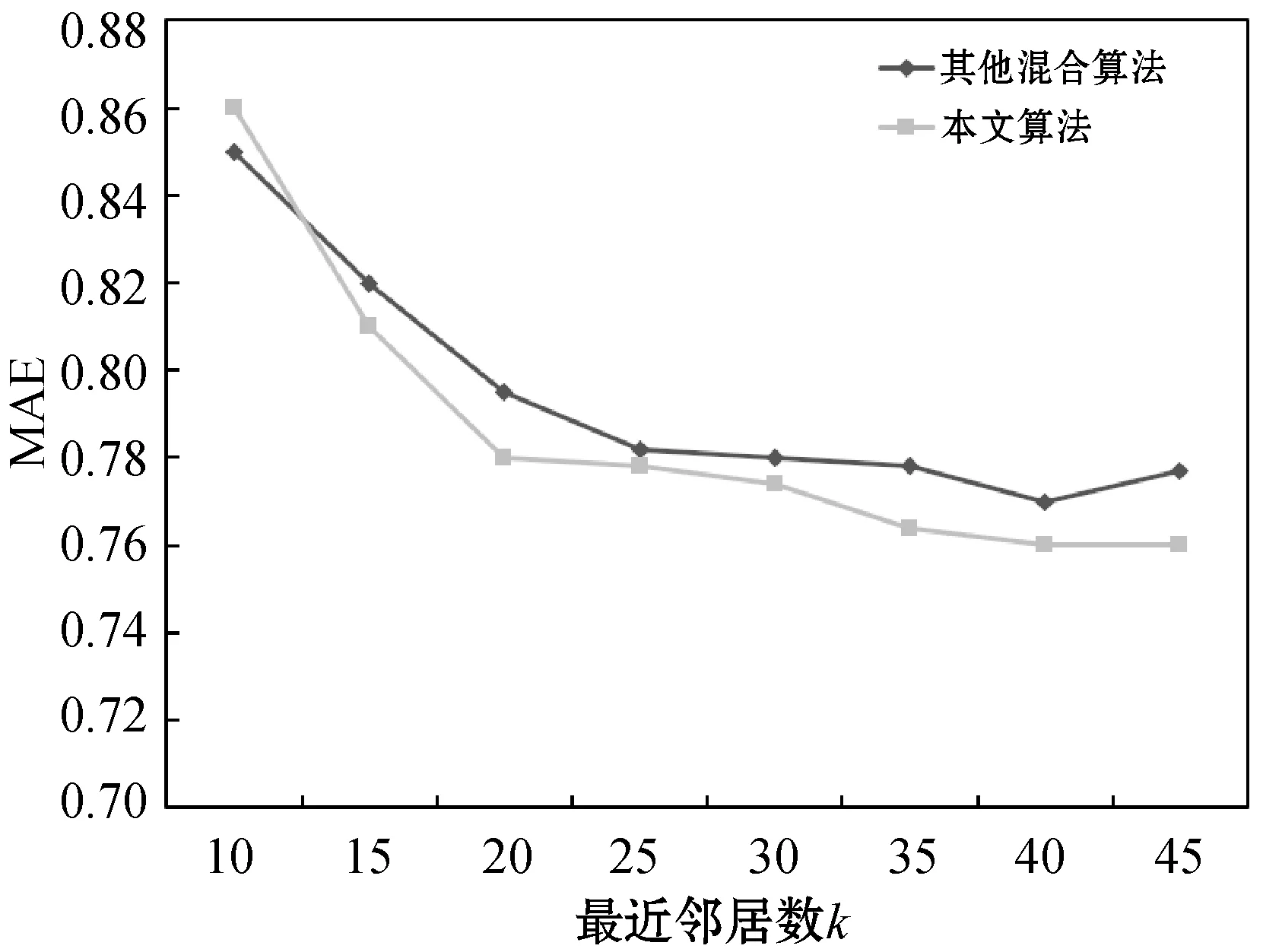
图5 不同混合推荐算法在不同k值下的MAE比较

可以看出当最近邻居数小于15时，本文算法的MAE值较大，当最近邻居数大于25时，本文算法的MAE值小于基于SVD和用户聚类的协同过滤算法研究[11]中的混合推荐算法。

5 结 语

为了对用户做更精准的视频推荐，本文提出一种基于改进的BiasSVD算法和聚类用户最近邻的协同过滤混合推荐算法。根据实验结果可以得出，本文算法可以改善矩阵的可扩展性问题，并能提高评分预测的准确度。尽管本文的研究已经取得了一定阶段性成果，但是对于处理数据的速度还有所欠缺，所以下一步将针对如何基于大规模用户评分矩阵来快速高效地预测用户评分问题，进行更深入研究。