基于变换域和形状特征的感知图像哈希算法
周晓炜 赵 琰,2*
1(上海电力大学电子与信息工程学院 上海 200090) 2(广西师范大学广西多源信息挖掘与安全重点实验室 广西 桂林 541004)
0 引 言
数字图像随着互联网技术的快速发展以及计算机的广泛应用已经渗入到生活中的各个角落,但其在传输过程中的安全性也受到了考验,市场上也出现了各种类似于Photoshop和美图秀秀等简单易用快速的图像编辑软件。数字图像在传输过程中很容易被替换或者篡改,图像接收端需要能够验证收到图像的安全性,这就引出了图像哈希的概念。图像哈希是指使用紧凑序列表示图像及其内容的技术。人们通过使用提出的哈希算法对接收图像进行处理得到哈希序列,计算其与从安全通道接收到的原哈希序列的距离来验证接收图像的安全性。一般情况下,图像哈希需要能够区分出相似图像和不同图像,即具有鲁棒性和区分性。
图像感知哈希算法的核心是图像特征向量的选取。近几年提出的图像感知哈希算法一般都是基于变换域和空域,而基于空域的哈希算法根据特征的选取又大致分为基于形状纹理特征和结合颜色信息的算法。
1) 基于变换域。文献[1]通过DCT变换构造基于颜色向量角的特征矩阵,再用LLE降维来构建哈希,算法对大部分内容保持操作都具有较好的鲁棒性,但对旋转、裁剪和缩放操作不够鲁棒。文献[2]提取图像在YCbCr空间的亮度Y分量进行Radon变换,对Radon变换后的系数进行一维DCT变换取第一AC分量构成行向量后提取统计特征作为哈希,算法使用Radon变换从而具有良好的抗旋转性能,但对亮度和对比度调整的鲁棒性和区分性不足。Tang等[3]通过对数极坐标变换和离散傅里叶变换从图像中提取具有旋转不变性的特征矩阵,然后使用多维尺度分析(MDS)将特征矩阵表示为哈希序列,算法对大角度旋转也具有不错的鲁棒性,但运行效率不高。Yan等[4]提出的基于四元数的哈希方法使用四元数傅里叶变换同时结合颜色和结构特征生成哈希,能够消除几何畸变对哈希序列的影响,检测出几乎所有类型的篡改,相对于之前多数算法只能检测出特定篡改在应用广泛性上有了很大提升。文献[5]对图像进行DCT变换后提取低频系数作为特征再通过DWT变换将其转换为紧凑哈希序列,算法有较低的哈希位数,但在旋转操作下只对小角度鲁棒。
2) 基于空域。(1) 基于形状纹理特征。文献[6]结合SVD和LBP的特性提出了SVD-CSLBP算法,提高了对内容保持操作的鲁棒性,但代价是对旋转操作的敏感性。文献[7]结合全局特征四元数Zernike矩和局部特征SIFT特征点来构造哈希,通过检测匹配SIFT兴趣点来定位篡改,算法可以检测定位对象插入、删除、替换、复制移动和剪切粘贴等篡改操作。文献[8]通过提取灰度图像的精确Gaussian-Hermite矩以及Gaussian-Hermite矩的不变量来构建哈希序列,算法除JEPG压缩操作不如Zernike矩鲁棒外,对其他内容保持操作尤其是噪声的鲁棒性都优于大多数比较算法。(2) 基于颜色信息。Qin等[9]提出基于环和基于块的策略对图像颜色矢量角提取特征从而生成哈希,算法相对于其他基于颜色矢量角的算法鲁棒性和区分性都有所提升,但对亮度和对比度的鲁棒性略有下降。文献[10]利用颜色向量角能够很好地区分色相和饱和度差异的特性,从归一化图像内最大圆内的颜色矢量角里提取直方图来构建图像哈希,算法的哈希序列不够紧凑,且对局部区域的篡改不够敏感。Tang等[11]将RGB彩色图像转换为HSI和YCbCr颜色空间,计算HSI和YCbCr各分量的块均值和方差,提取局部颜色特征然后计算块特征向量和参考特征向量之间的欧氏距离作为哈希值,但算法对旋转操作不鲁棒。文献[12]将图像进行ring分割后在感知均匀的CIE-L×a×b×颜色空间中提取每一环的统计特征构成哈希,该算法对旋转有较强的鲁棒性,但效率不高。
3) 其他方法。Tang等[13]首先将图像构建为一个稳定的三阶张量,然后使用Tucker分解将三阶张量分解为一个核张量和三个正交因子矩阵,将正交因子矩阵构造为哈希序列,算法对JPEG压缩和乘性噪声等内容保持操作有较强的鲁棒性。文献[14]对整幅图像提取SIFT特征点后将图像分为非重叠的若干子块,选取其中特征点个数较多的图像子块提取其颜色、纹理和形状特征形成最终哈希序列,该算法的碰撞率小于很多算法,但不适用于特征分布均匀的图像。
以上基于变换域的哈希算法忽略了人类对图像最直观的视觉感知特征,基于形状特征的算法和结合颜色信息的算法可以很好地描述图像轮廓和表示图像色度分量的变换,但对图像的表达都比较单一。为了能够从人类视觉感知上更完整地表示图像,从而提高算法的区分性和鲁棒性,本文从YCbCr颜色空间结合变换域NSCT分解和空域的形状特征Zernike矩提取图像的低频和高频信息共同构成哈希序列,并使用PCA降维降低低频图像的特征维度。实验结果表明本文算法具有不错的区分性和鲁棒性。
1 算法设计
1.1 哈希算法框架
本文哈希算法的步骤如图1所示,包括以下5部分内容:(1)
图像预处理;(2) 将经过预处理操作的图像三个通道分别进行NSCT一级分解,保留三个通道分解后的低频图像和Y通道的高频图像;(3) 将Y通道分解得到的高频图像经过Canny算子提取边缘后计算Zernike不变矩得到高频特征;(4) 在YCbCr空间,每个通道NSCT分解后的低频图像分别分割为64个子块并提取6个统计特征,构成一个18维的特征矩阵后使用PCA降维并压缩得到低频特征;(5) 联合低频特征和高频特征并利用密钥进行加密后构成最终的哈希序列。
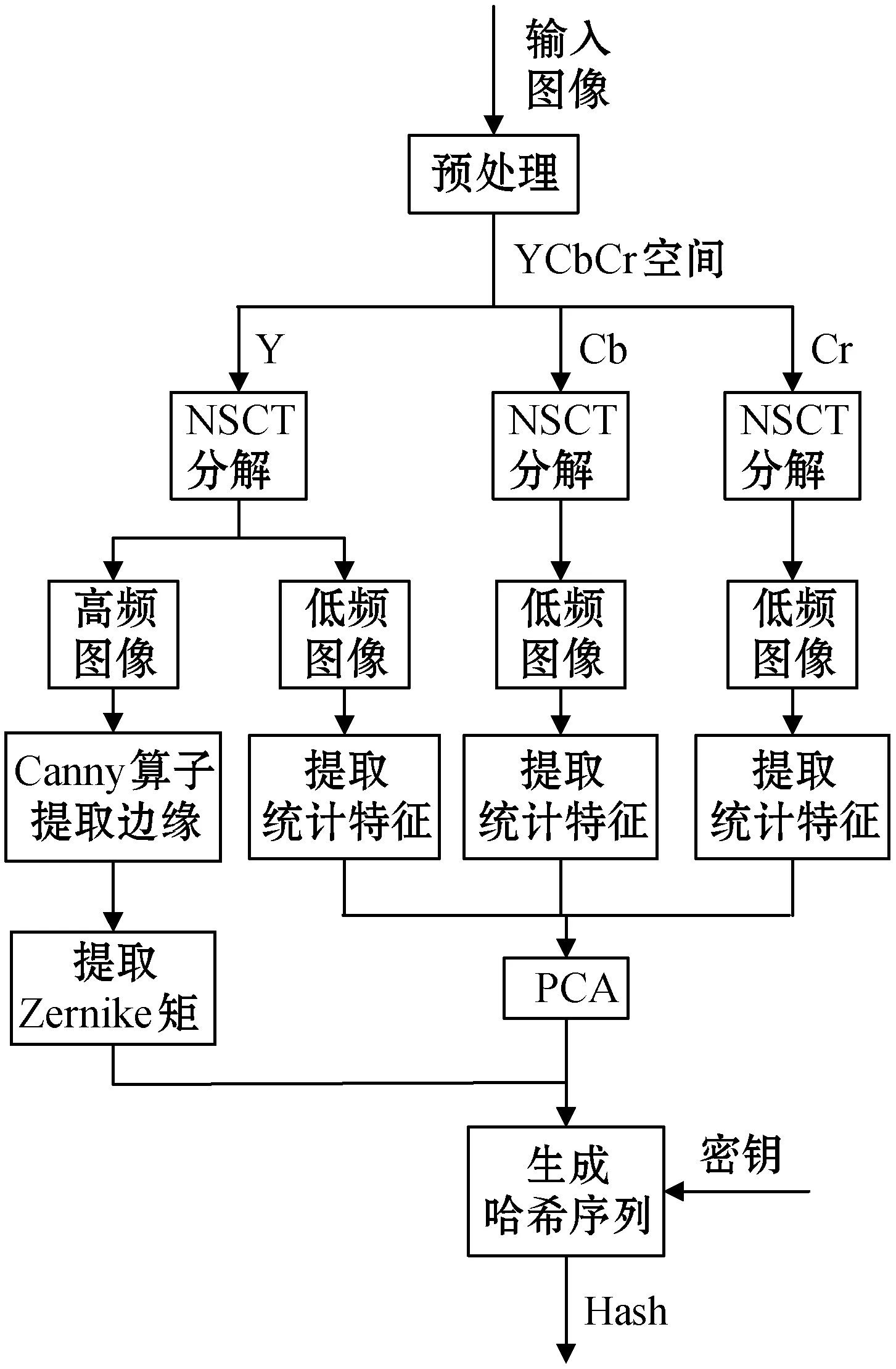
图1 本文哈希算法框架
1.2 图像预处理
首先使用双线性插值处理将图像的大小调整为256×256大小并进行高斯低通滤波来提高图像哈希算法对缩放操作和各种噪声的鲁棒性。如果输入图像是RGB彩色图像,因其颜色空间三个通道之间存在一定的相关性,而YCbCr空间具有和人的视觉感知一致性及色度相互独立的优点,因此将其转化到YCbCr空间。
1.3 图像特征提取
非下采样轮廓波变换(NSCT)[15]是一种二维图像变换技术,相较于其他变换方法它能够将图像分解为低频部分和多方向的光滑轮廓。NSCT通过非子采样金字塔滤波器和非子采样方向滤波器组两种滤波器进行工作,在原始图像上应用非子采样金字塔滤波器,去除低通和高通子带,在带通滤波器上应用NSDFB进行分解。
首先对经过预处理操作的图像的Y、Cb、Cr通道分别进行NSCT一级分解,保留三个通道分解得到的低频图像和Y通道分解得到的高频图像。
1.3.1形状特征提取
Zernike函数[16]最早由Frits Zernike提出,具有简单的旋转不变性,它的核是一组单位圆上定义的完备正交基。一幅数字图像f(x,y)的重复度为q、阶数为p的二维Zernike矩函数定义为:
(1)
式中:dxdy=rdrdθ,-π≤θ≤π。
Zernike矩可以用来描述图像的形状特征,而图像的高频分量往往是图像亮度变化剧烈的地方,YCbCr空间中Y通道是亮度分量,Cb通道反映的是蓝色信号部分与RGB信号亮度值之间的差异,Cr通道反映了RGB颜色模型中红色信号部分与RGB信号亮度值之间的差异,所以算法仅对预处理后的图像Y通道进行NSCT分解得到的高频图像使用Canny算子提取边缘得到二值图像,接着对二值图像提取Zernike矩作为中间哈希序列H1。这里提取9个Zernike不变矩(Z00,Z11,Z20,Z22,Z31,Z33,Z40,Z42,Z44)作为高频特征,所以H1的长度为9。
1.3.2统计特征提取和降维
本文算法将三个通道得到的低频图像分成n×n个子块后提取每个子块的6个统计特征,分别是均值、标准差、平滑度、三阶矩、一致性、熵。每个通道可以得到一个6×n的特征矩阵,结合3个通道的特征矩阵得到一个18×n的特征矩阵X。
通过主成分分析[17]忽略次要的分量可以将18×n的特征向量矩阵X降维构成一个k×n的矩阵Y。通过计算矩阵Y各行与参考向量y0的二范数来将矩阵Y压缩为一个哈希序列。步骤如下:
首先,设Y=[y1,y2,…,yN],计算参考向量y0=[y0(1),y0(2),…,y0(k)]T,其中y0(i)为向量y0的第i个元素,定义为:
(2)
式中:yj(i)为向量yj的第i个元素。
接着计算矩阵Y各行向量yj与参考向量y0的二范数,定义为:
(3)
将向量d量化为与中间哈希序列H1同一量级的序列即为哈希序列H2,H2的长度为n。
1.4 哈希构建
结合高频图像提取形状特征得到的中间哈希序列H1和低频图像得到的中间哈希序列H2得到最终哈希h,即h=[H1,H2],所以h的长度为n+9。
1.5 相似性度量
为了确保图像传输过程中未被替换或篡改,需要对收到的图像进行安全认证。如图2所示,首先通过本文哈希函数对收到图像提取哈希序列h1,然后计算h1与从安全通道传输的图像原哈希序列h2之间的欧氏距离。当欧氏距离d≤T时,图像通过安全认证,否则安全认证失败,其中:T为一个预先给定的阈值。欧氏距离公式为:
(4)
式中:h1(i)表示收到图像所提取的哈希序列的第i个值;h2(i)表示安全通道传输的图像原哈希序列的第i个值。
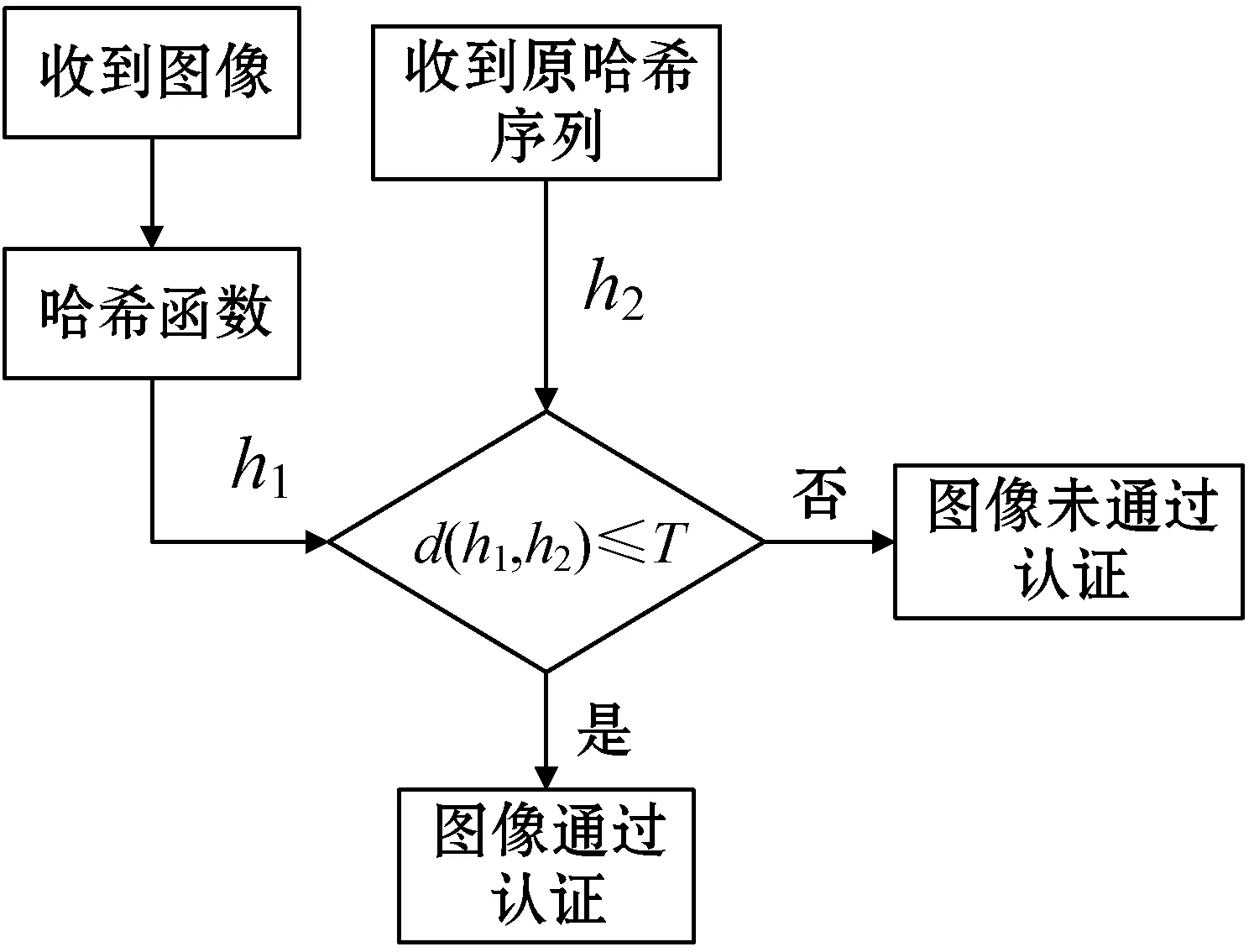
图2 图像安全认证流程
2 实 验
实验中的参数设置如下:3×3高斯低通滤波的标准差设置为3,低频图像的分块数n=64,PCA降维中取k=5,所得到的哈希长度为73。
2.1 鲁棒性实验
将图3所示的Airplane、House、Lena、Baboon和Peppers五幅标准图像作为鲁棒性实验样本,利用Photoshop、MATLAB和光影魔术手等图像编辑软件对五幅标准图像进行内容保持操作,所采用的内容保持操作及参数如表1所示。

图3 五幅标准图像
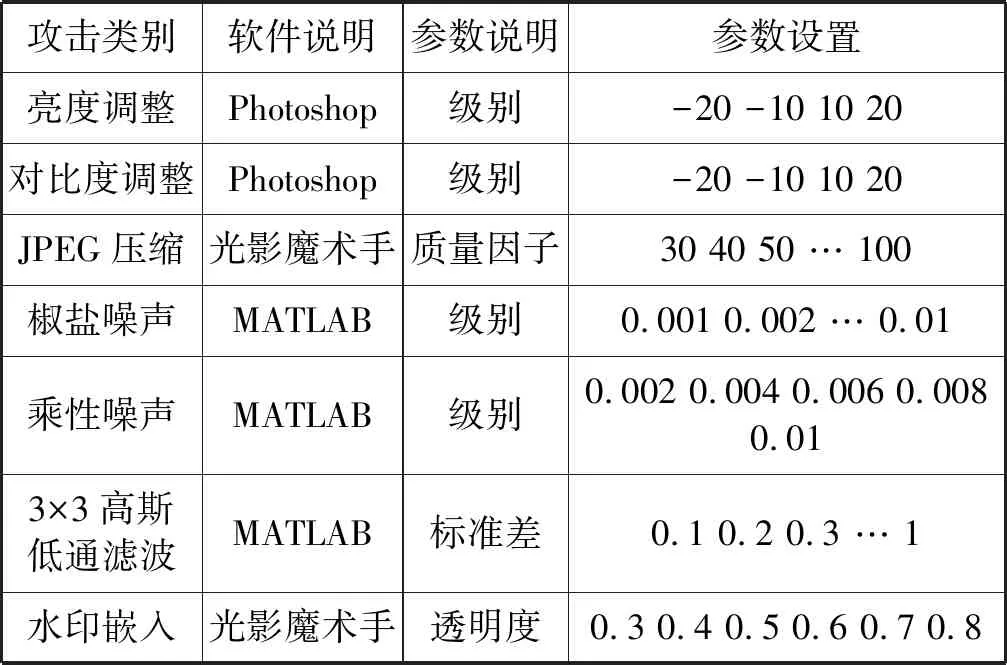
表1 内容保持操作参数
实验结果如图4所示,其中横坐标表示不同参数下的各种内容保持操作,纵坐标表示内容保持操作图像哈希序列与原图像哈希序列之间的距离。可以看出,内容保持操作图像与原图之间的哈希距离比较集中,基本都小于60,个别操作与原图距离较大,但不超过80,远小于后文设置的区分相似图像和不同图像的最优阈值。
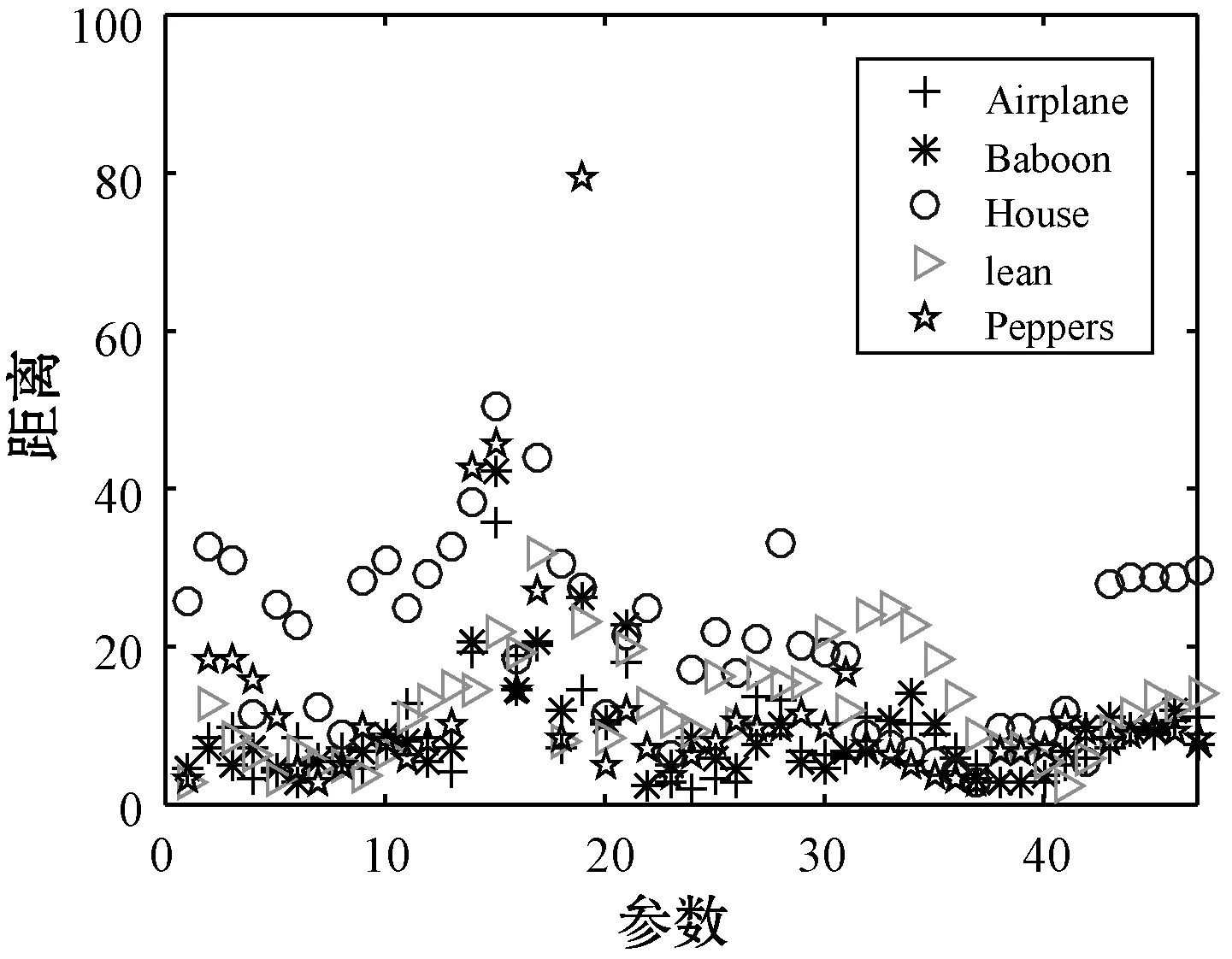
图4 鲁棒性实验结果
2.2 区分性实验
算法的区分性实验样本来自于华盛顿大学Ground Truth Database图库[18]中的700幅图像和数据库VOC2007[19]中的300幅图像构成的1 000幅不同图像图库。1 000幅图像两两之间构成不同图像对,不同图像对的总数为499 500,通过对1 000幅图像进行如表2所示的处理,每幅图像与其生成的14幅内容保持操作图像共15幅图像两两之间构成相似图像对,相似图像对的总数为105 000。实验结果如图5所示,横坐标为图像对之间的欧氏距离,纵坐标为不同欧氏距离的图像对的数目。不同图像对之间的哈希距离分布用实线表示,相似图像对之间的哈希距离分布用虚线表示。可以看出,虚线和实线之间只有少量相交,即相似图像和不同图像只有少量图像会被判断错误,所以可以通过合适的阈值来区分相似图像和不同图像。这里引入检错率和碰撞率[20]来衡量哈希算法的区分性,计算式分别如下:
(5)
(6)
式中:阈值T确定时,NE为所有相似图像对中被判断为不同图像对的数目;NC为所有不同图像对中被判断为相似图像对的数目;NS、ND分别为相似图像对的总数目和不同图像对的总数目;PE为检错率;PC为碰撞率。
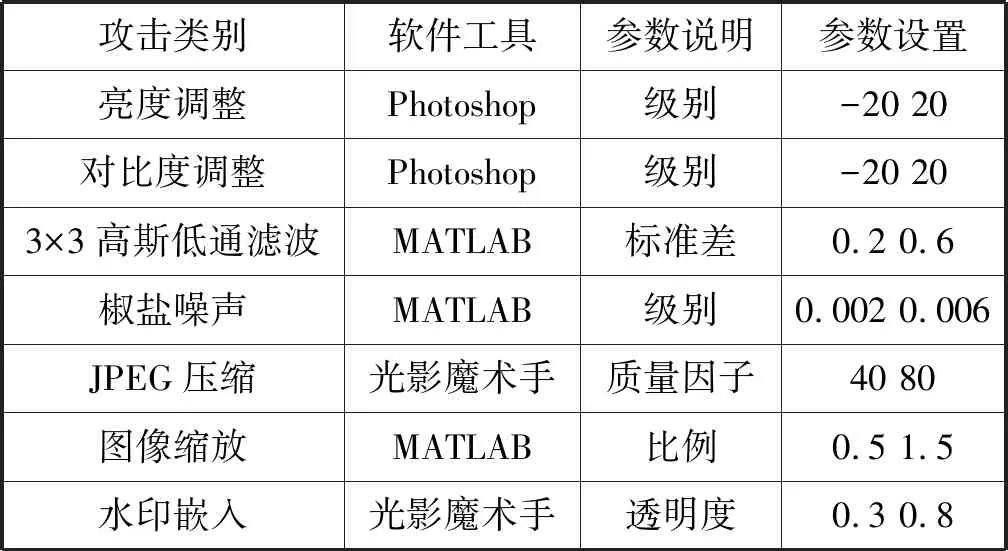
表2 不同攻击参数
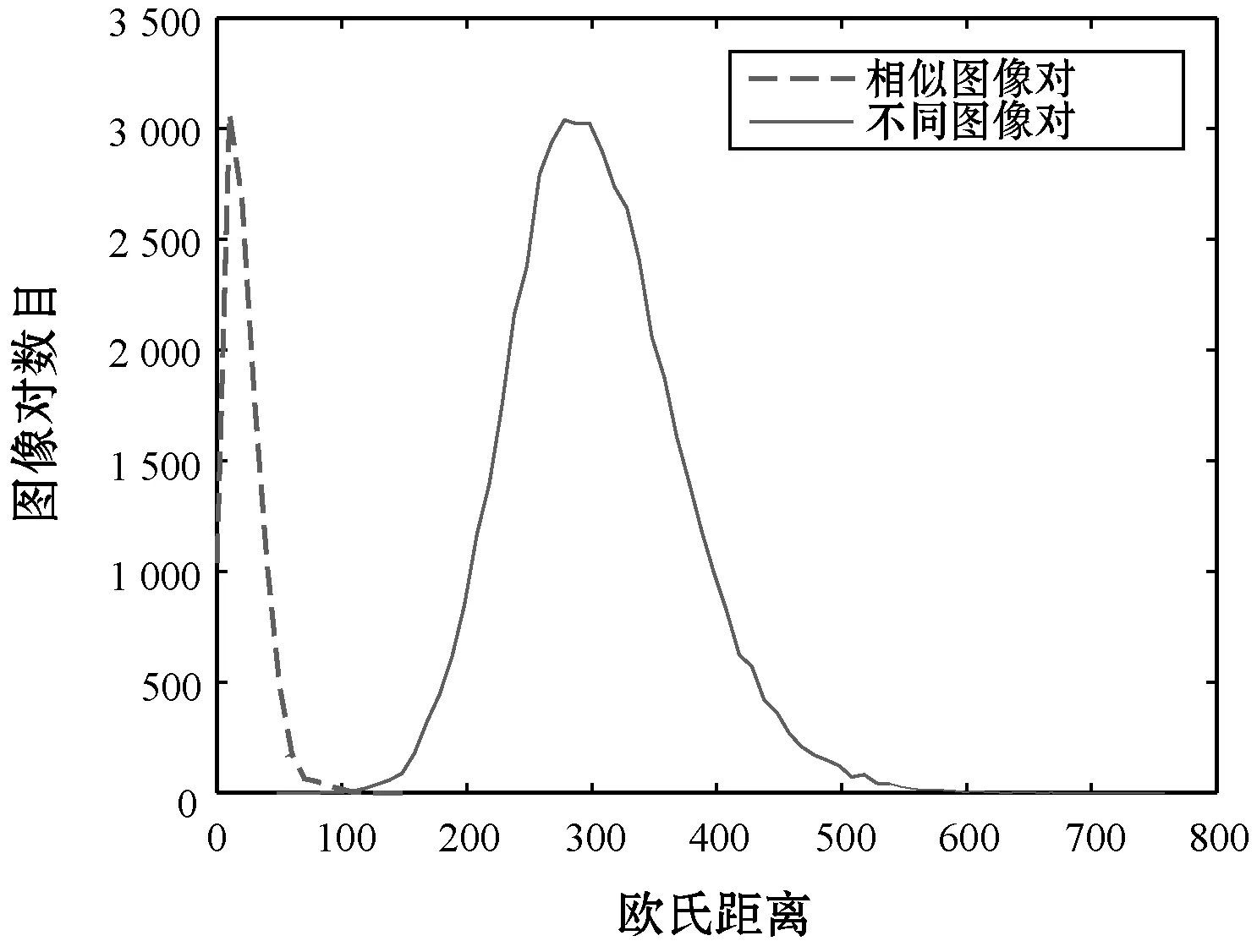
图5 区分性实验结果
不同阈值下的PC和PE如表3所示。可以看出,检错率与碰撞率呈反比关系,碰撞率增大,检错率减小。这是因为相似图像之间的哈希距离与不同图像之间的哈希距离有部分相交,所以阈值过小会有更多的相似图像被误判为不同图像从而拥有更大的碰撞率,阈值过大则会导致不同图像被误判为相似图像的数目增多,检错率随之增大。当阈值T为124时,检错率和碰撞率都相对较小,所以区分相似图像和不同图像的最优阈值可以设为124。

表3 不同阈值下的PC和PE
2.3 安全性实验
本文使用标准图像中的Lena图像来测试本文哈希算法的安全性,如图6所示。对原图像使用500个错误密钥生成错误的哈希序列,与正确密钥生成的哈希序列计算欧氏距离,得到的结果远远高于2.2节设置的最优阈值124,使用错误密钥所生成的哈希会被判断为未通过安全认证,所以本文算法具有较高的安全性。
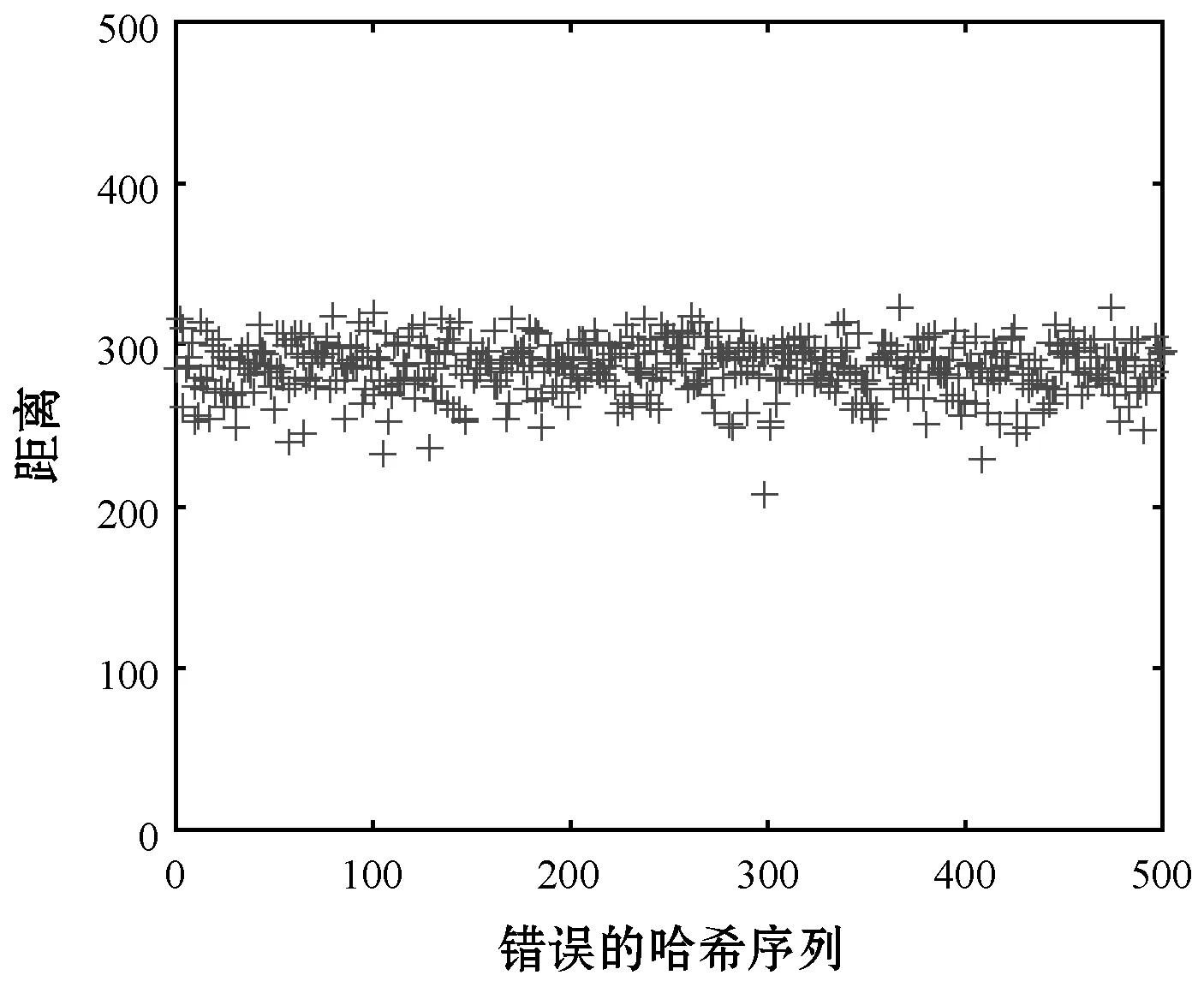
图6 安全性实验结果
2.4 不同算法对比
将本文算法与DCT-DWT算法[5]、Local color算法[11]、Ring partition算法[12]和Tensor decomposition算法[13]进行对比。为了进行公平的比较,使用2.2节采用的499 500个不同图像对和105 000个相似图像对来验证它们的分类性能,在同一台配置为Intel(R) Core(TM)i5-3230M CPU @2.60 GHz和4.00 GB内存的计算机的MATLAB R2015b平台上对各个比较算法进行仿真。使用ROC曲线[21]和算法速度来衡量算法的优劣,其中两个重要指标正确接受率PTPR和错误接受率PFPR定义如下:
(7)
(8)
式中:nTPR为所有相似图像对中被正确判断为相似图像的数目;NTPR为相似图像对的总数目;nFPR为所有不同图像对中被错误判断为相似图像的个数;NFPR为不同图像对的总数目。可以看出,性能好的算法应该拥有更高的正确接受率和更低的错误接受率。而在ROC曲线中,x轴为PFPR,y轴为PTPR,所以算法的ROC曲线越接近坐标轴的左上角则其分类性能越好。
图7所示为不同哈希算法的ROC曲线比较。可以看出本文算法所生成的ROC曲线在所有算法中最靠近坐标轴左上角,说明本文算法拥有更高的正确接受率和更低的错误接受率,即分类性能最好。
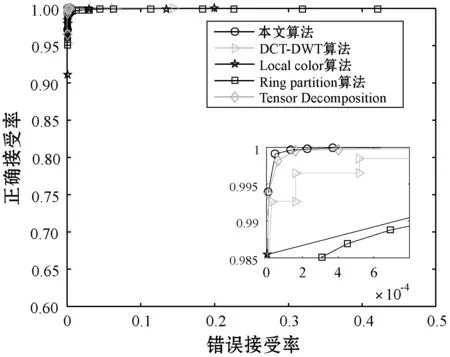
图7 不同算法的ROC曲线
图8所示为不同算法相似图像之间哈希距离和不同图像之间哈希距离分布图。视觉相似的图像生成哈希相互之间的距离与不同图像所生成哈希之间的距离重叠部分越多,算法的区分性越差。可以看出,本文算法两条曲线相交最少,也就表明其区分性最好。
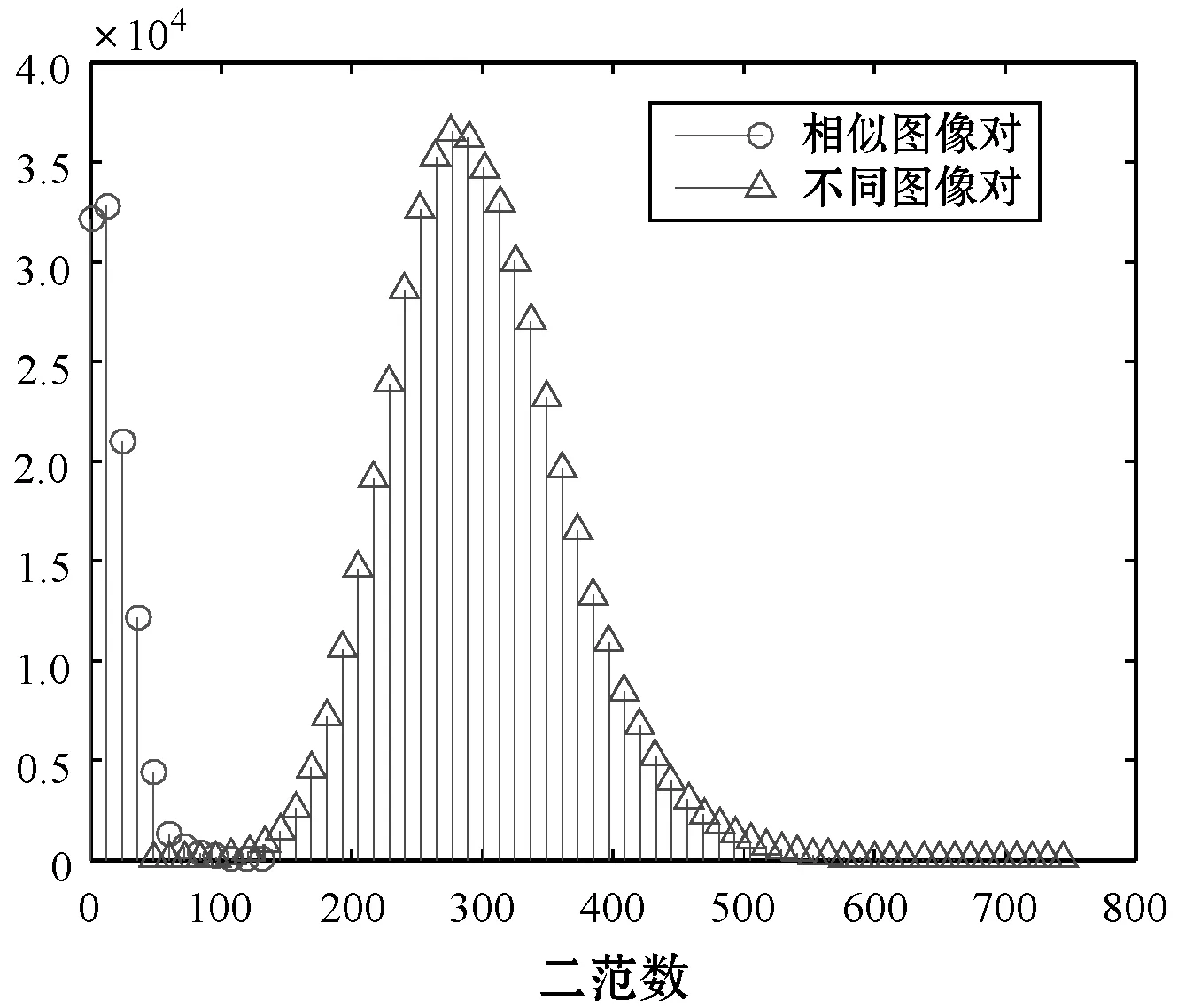
(a) 本文算法
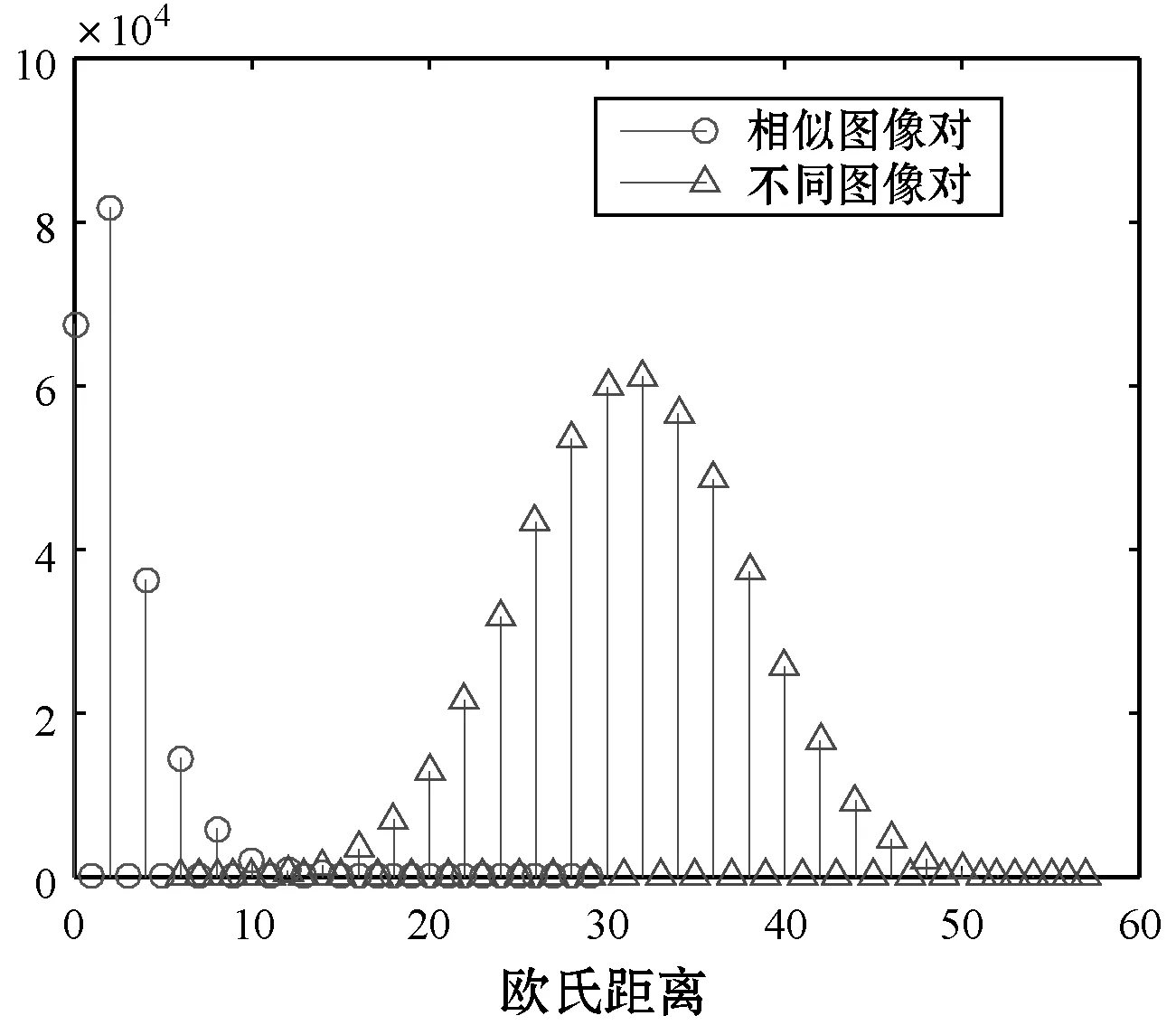
(b) DCT-DWT算法
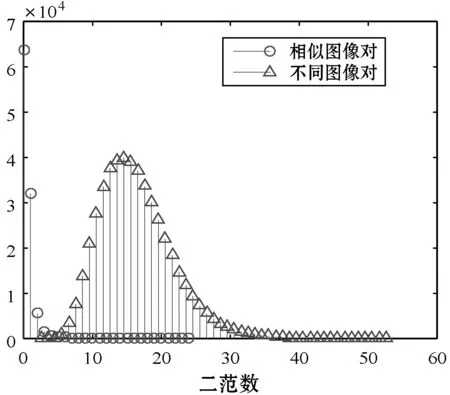
(c) Local color算法

(d) Ring partition算法
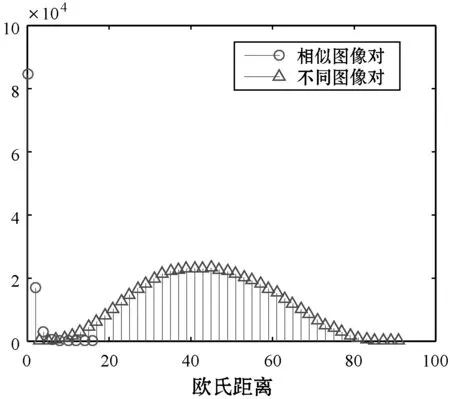
(e) Tensor Decomposition算法图8 不同算法相似图像间哈希距离和 不同图像间哈希距离分布图
不同算法在上述平台上进行仿真中计算1 000幅图像生成哈希序列的平均时间如表4所示。可以看出,除Local color算法较本文算法稍快0.22 s,其他比较算法运算效率均差于本文算法,但本文算法的区分性能在所有比较算法中最好,更远远优于Local color算法。综合考虑运算效率和哈希性能的前提下,本文算法在保证效率的同时分类性能最优。
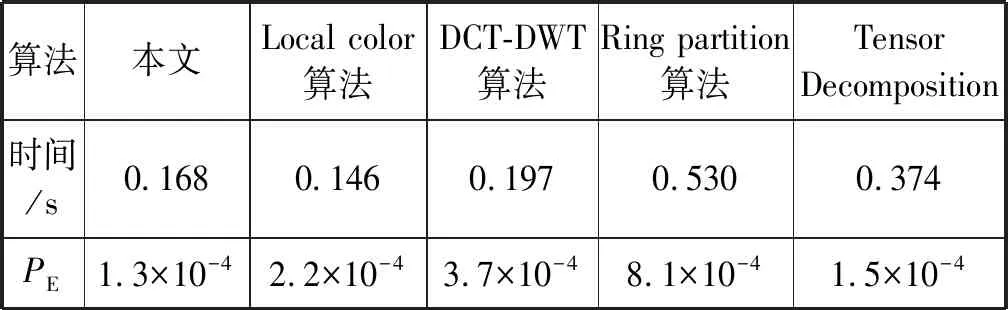
表4 各算法运行时间
3 结 语
本文提出了一种基于NSCT分解和Zernike矩的感知图像哈希算法,在YCbCr颜色空间将NSCT分解得到的低频图像提取统计特征使用PCA降维得到低频特征,NSCT分解得到的Y分量的高频图像提取边缘后使用Zernike矩表示形状特征,结合低频和高频特征生成哈希。
算法基于变换域在不同颜色空间提取图像的统计特征和形状特征来生成哈希,多角度多方位地表示图像内容,更符合人类视觉感知特性。实验表明该算法相较几种对比算法速度较快,区分性更好,在保证哈希性能的同时实现分类性能最优。

