基于COMSOL的流注头部分叉过程仿真与分析

朱毅佳 朱 武* 张佳民

1(上海电力大学电子与信息工程学院 上海 200090) 2(上海电力大学自动化工程学院 上海 200090)

0 引 言

随着我国特高压输电工程的深入开展，电压等级不断升高，高压设备空气间隙放电极易发生，对电网的安全、稳定运行构成潜在的危害。如何优化输变电工程的空气间隙结构一直是高电压工程亟待解决的核心问题之一[1]。因此，对空气间隙放电特性的研究具有重要的理论价值和实际应用价值。20世纪以来，国内外学者对气体放电的研究不断深入，一般认为，流注是一种以弱电离、低温等离子体丝的形式传播的放电现象，其头部由强电场驱动。在许多的气体放电实验中，放电通道在发展过程中分裂成若干条树枝一样外形的放电通道，这种现象被称为流注分叉[2]。流注在唯象层面的分叉图样可以通过分形生长模型(DBM)生成，然而这种唯象层面的生成方法并没有反映出流注分叉出现的物理原因。关于流注分叉现象的原因，文献[3-5]认为流注头部分叉是流注头部空间净电荷薄层在发展过程中出现Laplace不稳定性的表现。净电荷薄层与流注前方电场形成正反馈，其越接近平坦，不稳定性就越高。文献[6-7]给出了由Laplace不稳定性导致流注分叉的物理图像。Li等[8]采用粒子模型研究大气中光电离对流注形成和传播的影响，获得了流注的分叉结构。

纵观流注放电的研究现状，描述放电过程的流体模型仍是流注数值仿真的常用手段。张赟等[9]采用伽辽金有限元法求解气体放电流体模型，结合FCT方法抑制计算误差，提高了计算精度和效率。Li等[10]与Teunissen博士和Ebert教授合作，开发出一套流注放电的三维粒子仿真模型，反映真实的放电结构特征。

本文通过对流扩散方程建立流体力学模型，将初始电离区域形状简化为两个具备高斯分布的初始电离区域的叠加，使用COMSOL Multiphysics软件在二维笛卡尔坐标系中对标准大气压下板-板电极结构中流注放电的过程进行模拟，目的是研究初始电离区域形状和电压对流注分叉情况的影响，观察流注通道的形成发展过程并对流注放电的头部分叉情况做出预测。

1 仿真模型

1.1 物理模型

搭建板-板电极间均匀电场的模型框架如图1所示。其中：阴极和阳极为两平行矩形板，间距d为10 mm，背景气体被简化为N2-O2体积比为8 ∶2的氮氧混合气体，气压p为101 kPa，环境温度设为300 K。

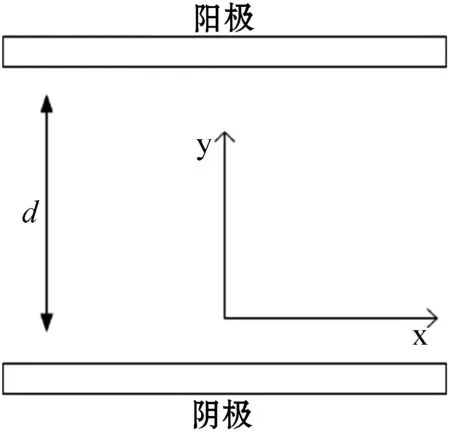
图1 平行板模型x-y截面图

在二维笛卡尔坐标系中，阳极(电压为+U)位于y=10 mm处，阴极(接地)在y=0处。

阴极表面的初始电离种子沿径向和轴向均满足高斯分布[11]如下：

(1)

为了更好地描述初始电离区域形状，将两个满足高斯分布的电离种子叠加构成一个整体。

描述该整体的高斯公式为：

(2)

式中：ne和np分别是放电过程中的电子数密度和正离子数密度；n0=2×1018m-3表示初始种子团的密度，即初始预电离水平；±x0是两个高斯中心的横轴坐标，令D=2x0；σy和σx是初始电子分别在y轴和x轴方向的特征尺寸，表示其分布的空间宽度。

1.2 化学反应模型

为进一步探讨流注分叉情况和相关电子密度的关系，本文以电子和正负离子在电场中的漂移扩散反应为流注模型的控制方程,以标准大气压下的流注为研究目标，采用仿真软件COMSOL Multiphysics的等离子体模块来模拟流注的形态。

虽然文中的空气已做简化处理，但氮氧混合气体中生成的化学反应种类繁多且复杂，分析全部的反应意义不大，本文选取了具有代表性的反应模型，展示了包括弹性碰撞、电离碰撞、相应附着反应和粒子间反应在内的21种化学反应，如表1所示。

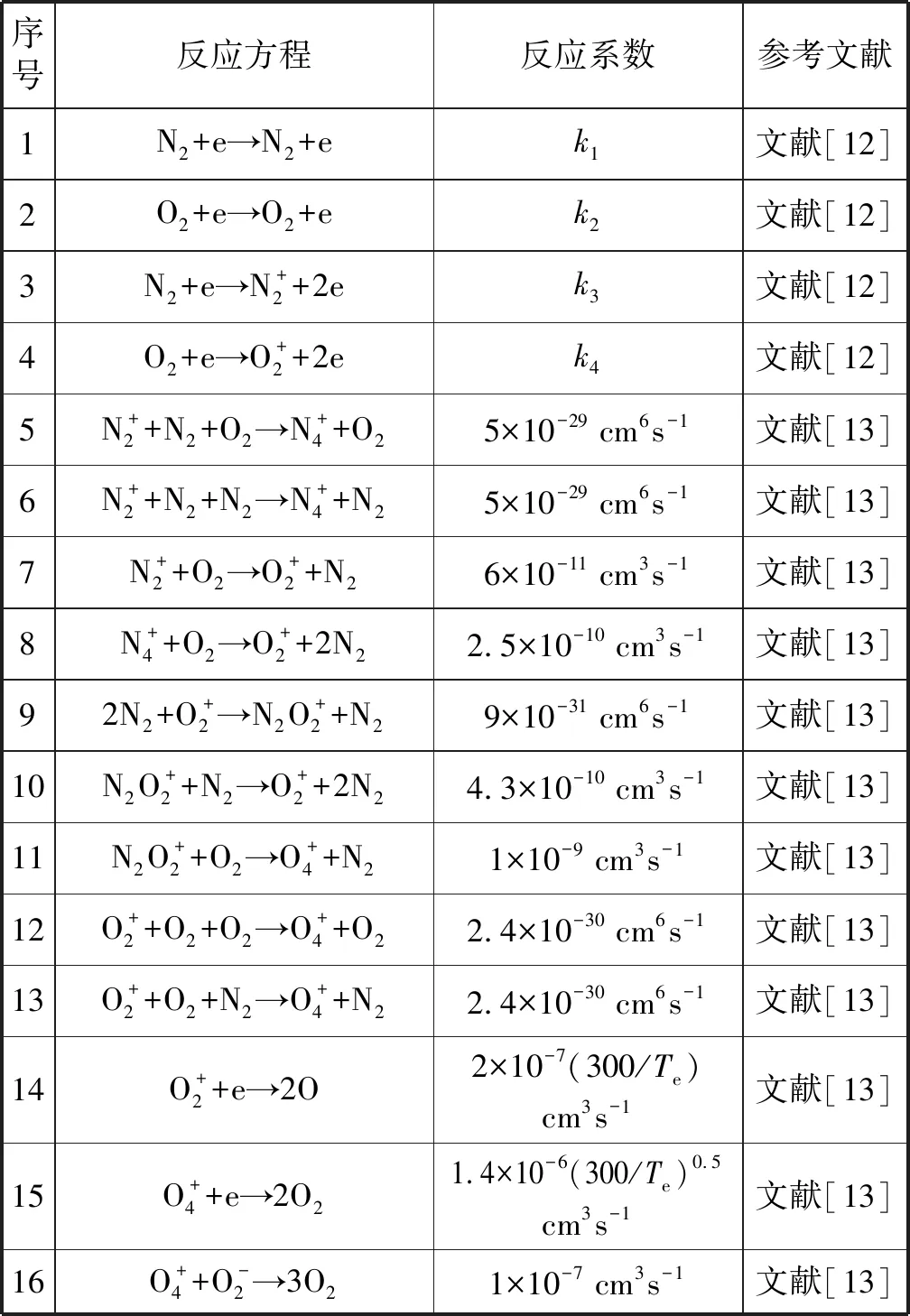
表1 计算中考虑的化学反应式

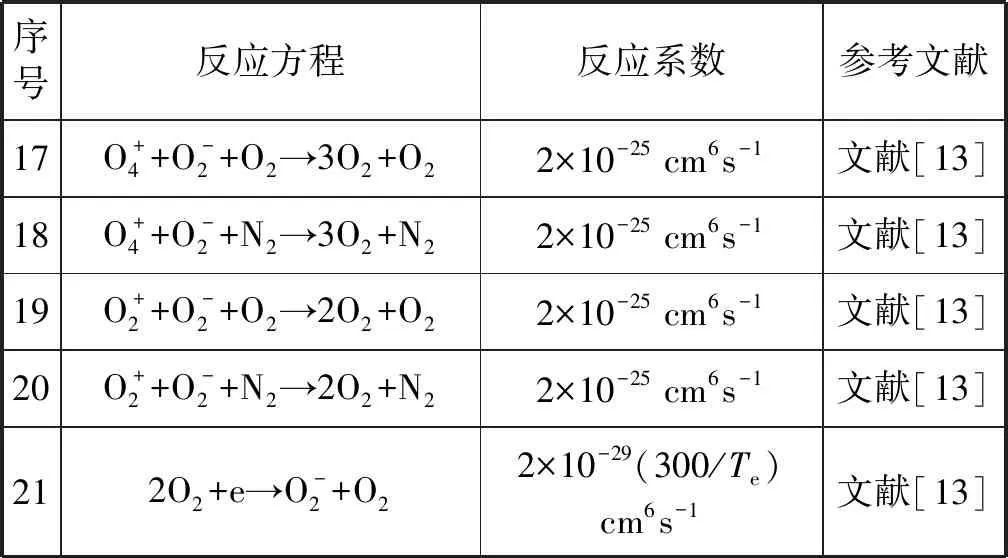
续表1

弹性碰撞和电离反应速率k1-k4及有效电子温度Te(单位为K)由BOLSIG+软件求解玻尔兹曼动力学方程计算得到。反应方程5-21的反应系数为常数来自文献[13]。

1.3 方程的边界条件及光电离

本文采用传统流体动力学模型，其由粒子的连续性方程(又称对流扩散方程)耦合电势的泊松方程组成，光电离则作为源项加在电子和正离子连续性方程上[14]。

由Hagelaar等[15]提出的电极表面处的电子通量边界条件为：

(3)

(4)

在实际应用中可简化为：

(5)

式中：E为场强；μe为电子磁矩；Γe为电子通量；n为电极表面的法向量；re为经典二次电子反射系数；vth是电子的热力学速度；kB为玻尔兹曼常数；αe是方向函数(当电子通量指向电极时为1，相反时则为0)。

电极处的离子通量可设置为[16]：

(6)

式中：Γk为离子通量；nk和mk为第k类离子的离子密度和离子质量；Tk为第k类离子的温度；γk为离子在电极表面衰变成中性的反应系数，表示反应的概率。

在非电极边界上则应用零梯度密度边界条件：

n·(∇ni)=0

(7)

本文中光电离项的计算是选取了文献[17]中的三项Helmholtz模型以及文献[18]中使用过的模型。三项Helmholtz模型计算结果准确，在远离表面的区域，它的计算效率更高。在不考虑边界表面光电离作用的情况下，利用Dirichle边界条件为0来降低计算成本[19]。

在该仿真计算中最细网格(靠近对称轴x=0)设置为0.1 μm，元素总数大约为107。采用MUMPS直接线性求解器进行求解，尽管该求解器的内存开销大，但其鲁棒性强。本文所有仿真结果均使用Intel(R) Xeon(R) E5-2637 v3处理器，且需要10～20个小时来模拟流注的发展过程。

2 仿真结果与讨论

2.1 初始电离区域形状对流注发展的影响

为探讨距离D其临界值的意义和相关电子密度的影响，并进一步探究种子解的包络面和流注头部分叉之间的联系，本文根据式(2)绘制了特征尺寸σx=σy=0.45 mm时不同距离D下的初始种子包络面图，如图2所示。由图2(d)可明显看出：随着电子密度ne的增加(轮廓线由外及内表示电子密度依次增大)，包络面的轮廓逐渐由一个较大的类半圆缩小为两个较规整的小半圆。图2(a)-图2(d)中最内侧的线直观地显示了电子密度ne=1.5×1019m-3在距离D取不同值时的初始种子包络面示图。

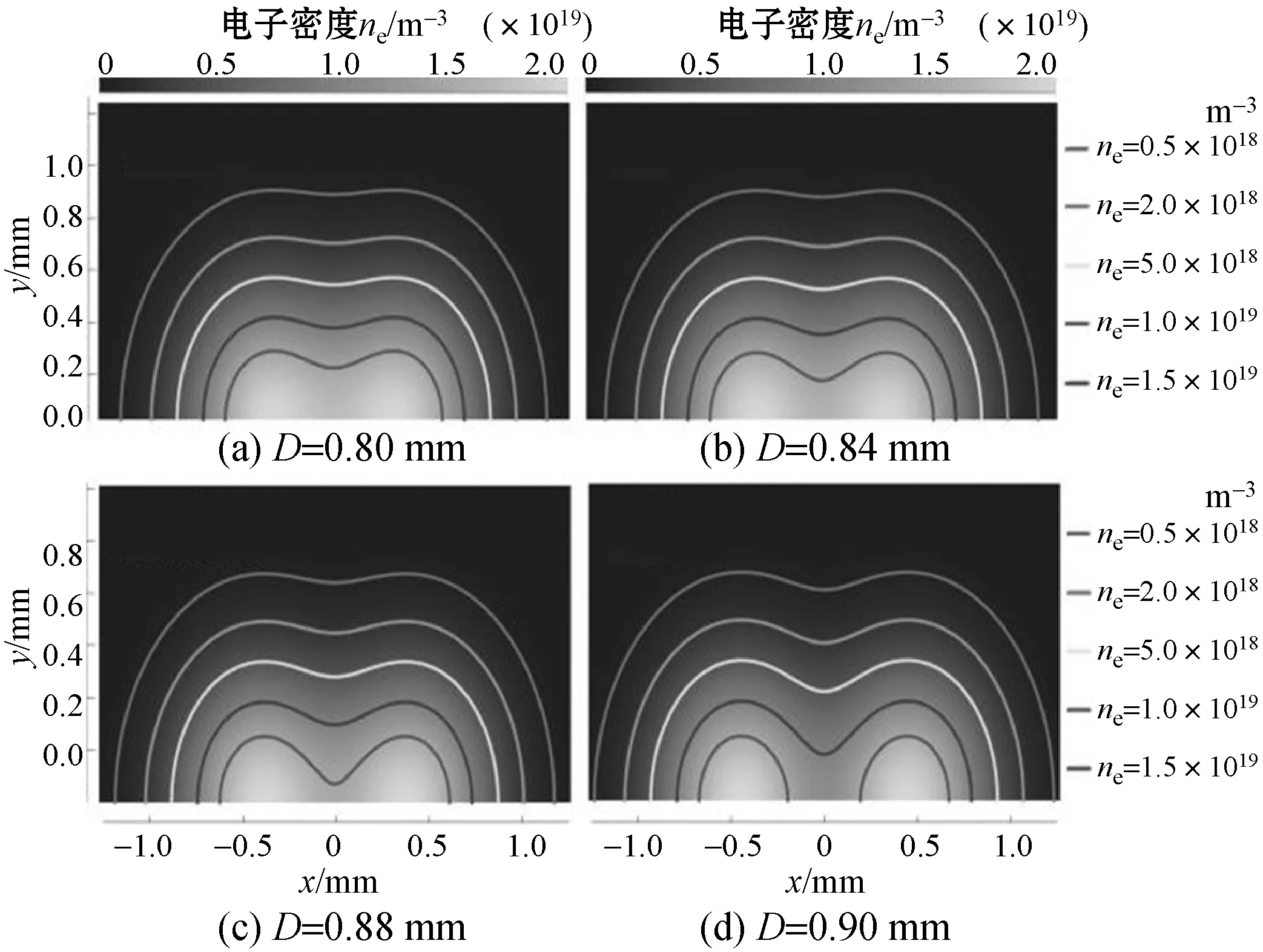
图2 初始种子包络面图

经观察发现，对于某一固定的电子密度值ne，只要适当提高距离D的值，包络面的轮廓线就会重复相似的转变过程(以图2所示的情景为例)：当电子密度ne=1.5×1019m-3时距离D从0开始缓慢增加时，包络面的轮廓中心开始向下凹陷，逐渐形成类驼峰状；当距离D大致介于0.88 mm到0.90 mm之间时，包络面的轮廓完全分裂成两个对称的半圆片，并且在刚好完成完全分裂(包络面的轮廓线经过原点)时，D达到其临界值。

这种通过识别与特定电子密度相关的指示轮廓线，利用轮廓线的几何形状以判断流注发展过程中头部是否分叉的方法即为包络面轮廓指示法。在模型基础参数固定不变的基础上，为获得距离D对流注发展动态的具体影响，本文模拟计算了一组不同距离的情况下电场背景均为38 kV·cm-1的电子密度分布图，如图3所示。

图3 不同距离下流注放电电子密度分布图

从图3(a)-图3(d)中可以明显看出，距离D在小于0.82 mm时，只有一条头部未发生分叉的流注由叠加的高斯种子产生，这表明距离D应存在一个临界值，低于该临界值时流注头部便不发生分叉。其中图3(a)中距离D=0的情况可视为实际只有一个初始高斯种子在发展，作为参考项。当距离D较小时(图3(b))，流注的头部未发生分叉的情况，而是在x轴方向上产生了横向扩展；当距离D到达其临界值(图3(d))时，流注头部开始出现分叉；当距离D增加到1 mm(图3(f))时，流注头部的分叉情况得到更加充分的展示。进一步增加距离D到1.4 mm时，这两个由于距离较远而完整分开的初始高斯种子将一条流注的头部分叉问题转化为两条流注相互作用影响的问题。由文献[20]中的结论可知，由于静电排斥的作用，两条流注在前进过程中会形成一定的角度，在以后的发展过程中不会产生融合的情况，仿真结果与该结论是一致的。而后当距离D再继续增加至更大值时，静电排斥效应将不再明显，两条流注将保持相互平行的状态向阳极发展，此时两条流注之间的相互影响可以忽略不计。

流注发展速率v也是描述流注时空特性的重要参数之一。根据仿真所得数据，可以确定流注头部的坐标位置，进而计算出流注的发展速率。

在38 kV·cm-1的电场背景下，距离D对流注的发展速率vave(前9 ns的平均速率)的影响如图4所示。通过分析可以发现，当距离D逐渐增大并超过0.4 mm时，其对vave的影响由微弱转变为迅速增大，并且vave的下降加速度在距离D介于0.8～0.9 mm间开始减缓，而流注头部分叉的临界值刚好处于这个范围内。但由于本文仿真数据的局限性，无法准确定位这个点。为此，本文探究出另一种指示方法。

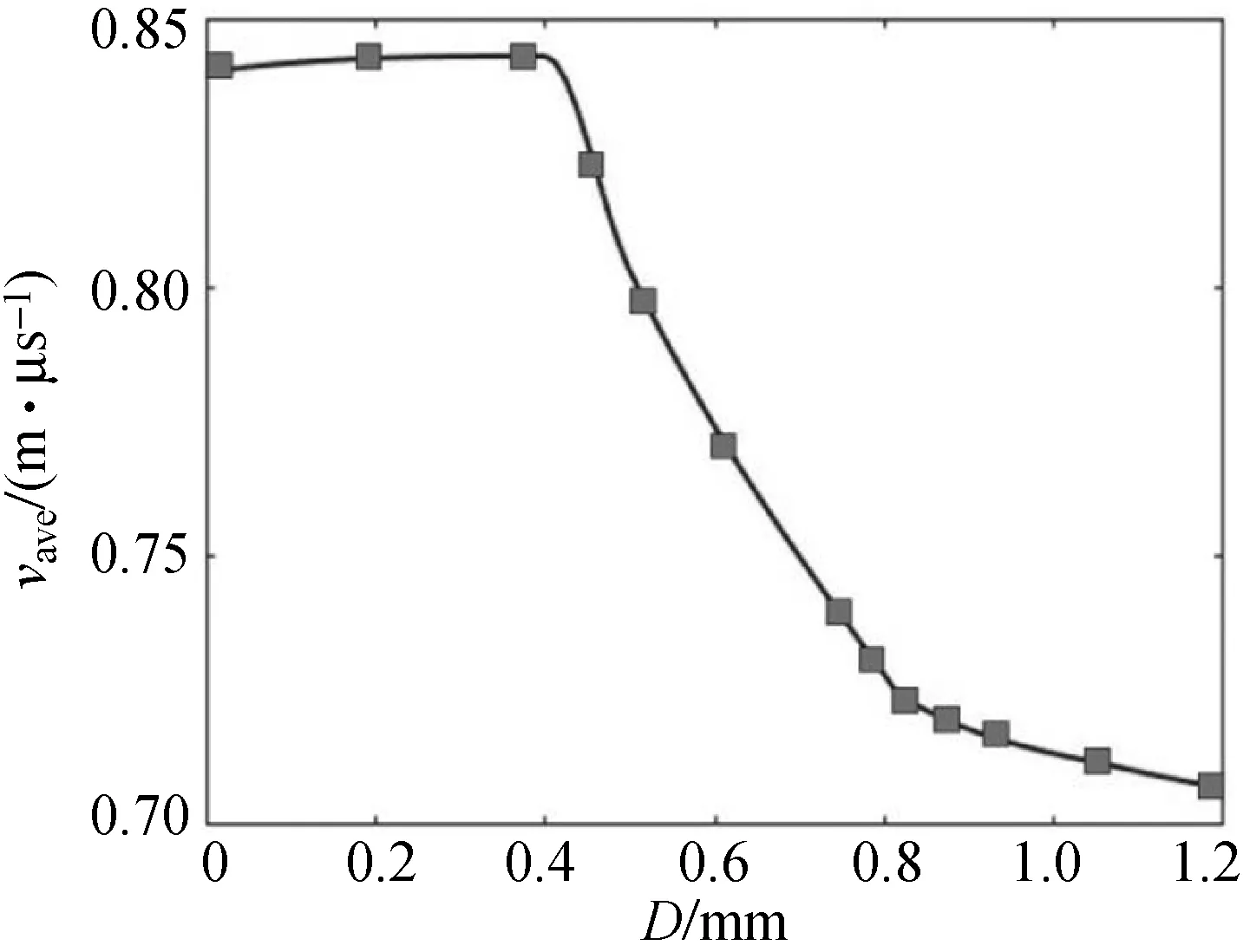
图4 流注平均速率示意图

2.2 电压对流注发展的影响

流注通道的发展特性与电场背景紧密相关，为获得电场对流注形成和发展的影响，本文基于上述模型模拟计算了3组不同参数的情况：1) 场强为36 kV·cm-1，时间设置为10 ns；2) 场强为38 kV·cm-1，时间设置为9 ns；3) 场强为40 kV·cm-1，时间设置为7 ns。仿真结果如图5所示。从仿真结果可以看出，在相同电压下增大距离D的值，流注在发展过程中仍存在着3种状态：1) 距离D低于临界值时，只有一条头部未发生分叉的流注由叠加的高斯种子产生；2) 距离D等于临界值时，流注的头部开始出现分叉；3) 距离D超过临界值时，流注头部的分叉更加明显。

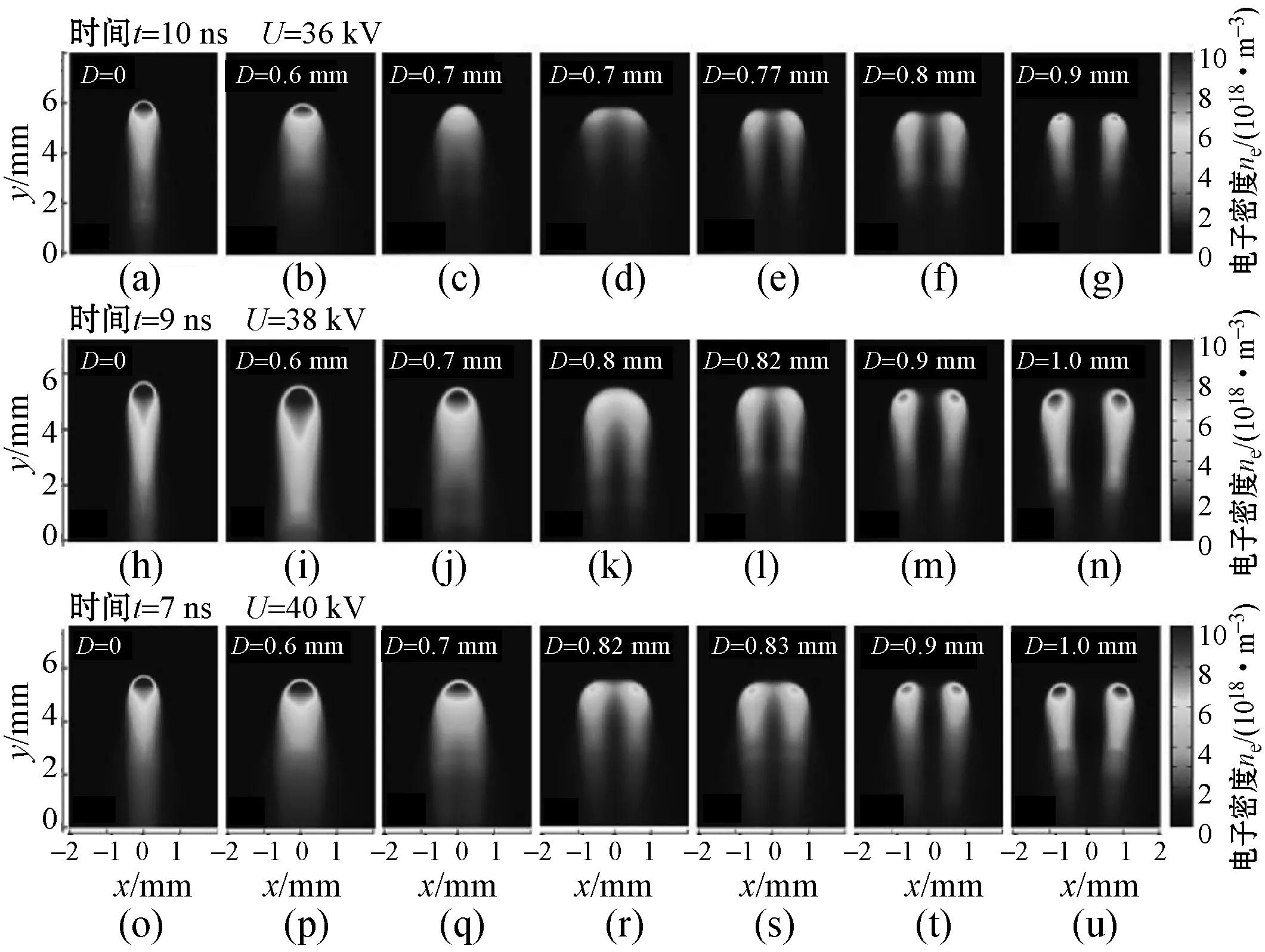
图5 不同电压下流注放电电子密度分布图

但在更高的电压背景下，流注的发展速率明显提高，流注头部的分叉现象出现得更晚，即距离D的头部分叉临界值与电压背景成正相关，随着电压U的增高而增大(U=36 kV时为0.76 mm，U=38 kV时为0.81 mm，U=40 kV时为0.83 mm)。这表明更高的电压或更大的场强对流注头部的分叉起抑制作用，更加促进了头部的融合(两条流注由两个叠加的高斯种子发展而来)。较为合理的解释是，在更高的电压背景下，光电离则更为突出，它抑制了初始种子头部包络面的不规则性。同时，更高的电压加速了流注的传播，这也不利于流注头部分叉的出现。

2.3 包络面轮廓指示法

基于上述对流注发展规律的总结，本文提出初始电离区域的包络面轮廓指示法，通过与特定电子密度相关的指示轮廓线的识别，判断流注发展头部分叉过程：当轮廓线的几何形状恰好分开为两个小半圆(指示轮廓线经过原点)时，对应的距离D即为流注头部分叉的距离临界值。

在电压U分别为36 kV、38 kV和40 kV的背景条件下，刚好落在横轴上完成分裂的曲线其电子密度分别为1.96×1019m-3、1.78×1019m-3和1.71×1019m-3。

根据包络面轮廓指示法，利用式(2)，可以解出对应的距离D，从而确定流注头部分叉临界距离：U=36 kV时为0.76 mm，U=38 kV时为0.81 mm，U=40 kV时为0.83 mm。计算结果与图5展示的仿真结果一致。

这种方法将初始电离区域形状的几何不规则性与流注放电的头部分叉现象联系起来，可以作为一种预测流注头部分叉的简单工具。

3 结 语

本文使用仿真软件COMSOL Multiphysics对空气中的负流注进行了二维模拟，研究了电压背景及初始电离区域的形状对流注发展的影响。主要结论如下：

1) 相同电压背景下改变初始电离区域形状会对流注的时空发展特性产生影响，随着距离的增大，流注的发展速率会减缓。

2) 随着电压降低，流注头部分叉的趋势更加明显，分叉的临界值更小。

3) 初步探究了初始种子电离区域形状的不规则性和流注放电头部分叉之间的关系：当高斯中心的距离较近、高斯种子重叠较多时，通过识别与特定电子密度相关的指示性轮廓线，利用轮廓线的几何形状可以可靠预测流注头部的分叉情况。