基于小信号谐波模型的VSC换流器谐波特性分析

杨城，李先允，颜云松，陈永华，王建宇

〔1.南京工程学院 电力工程学院, 江苏 南京 211167；2.南瑞集团(国网电力科学研究院)有限公司，江苏 南京 211106〕

0 引 言

随着新能源和多样化负荷的发展，电力电子变换器得到广泛应用，但其非线性开关特性却给电网造成了严重的谐波污染[1]。变换器的建模方法如状态空间平均法、dq域建模等，得到的模型一般为非线性模型或单谐波模型，难以用于高次谐波的分析[2-3]。

谐波状态空间建模方法因其能描述谐波分量及其耦合特性，被应用于电力电子建模及谐波分析中。文献[4]建立了晶闸管谐波状态空间(HSS)模型，发现谐波对变换器动态过程有重要影响。文献[5]基于单相整流的HSS模型，分析了谐波在控制器参数变化下的不稳定情况。文献[6]研究了DC/DC变换器中的谐波动态耦合行为。文献[7]对模块化多电平换流器开环和闭环下的HSS建模进行了系统研究。

本文采用HSS建模方法对电压源换流器(VSC)建模。将MATLAB中HSS模型的计算结果与PLECS仿真平台中搭建的模型结果进行了对比，验证了模型的准确性。基于该模型研究了变换器中谐波的耦合阻抗联系，分析了系统中含有不平衡谐波以及平衡谐波的谐波耦合情况。

1 HSS建模方法概述

非线性系统一般可以通过线性化将其视为线性时不变(linear time invariant，LTI)系统进行建模，如式(1)所示。

(1)

式中:x(t)为状态变量;u(t)为输入变量;A和B分别为输入矩阵和输出矩阵。

当系统中含有时变元件时，式(1)可改写为：

(2)

式中:A(t)和B(t)是随时间变化的动态矩阵。若时变元件随时间周期性变化，可以通过傅里叶级数来表达，如式(3)所示。

(3)

式中:k为谐波次数;Xk为k次谐波傅里叶系数;ω0为系统基频。

为研究动态特性，采用指数调制周期信号的形式表达，如式(4)所示。

(4)

将式(4)代入时变的状态空间方程中，即可得到HSS模型的表达式，如式(5)所示。

(5)

式中：Xn为状态变量;Yn为输出变量;Um为输入变量;An-m、Bn-m、Cn-m、Dn-m为时不变的状态、输入、输出和关联系数。

此时包含了所有的频率信息，通过HSS模型计算得到的结果通过式(6)可以转化到时域。

x(t)=Q(t)X

(6)

其中：

Q(t)=[e-jhω0t…，e-jω0t,1,ejω0t,…ejhω0t]

X=[X-h(t)…X-1(t)X0(t)X1(t)…Xh(t)]T

式中：Q为频率转移向量;X为状态变量集合。HSS模型使得基于周期变化的非线性时变系统转化成了一个定常系数矩阵的线性系统，是一个适用广泛且精确的模型。

2 VSC换流器HSS建模

2.1 VSC换流器小信号HSS模型

VSC换流器的拓扑结构如图1所示。图1中：vpcc为并网点电压；vc为变换器交流侧电压;vdc为变换器直流侧电压;Rg为线路等效电阻；Lg为滤波电感;ig为并网电流;Cdc为直流侧电容;Rdc为直流侧等效阻抗;PWM为变换器开关调制信号。

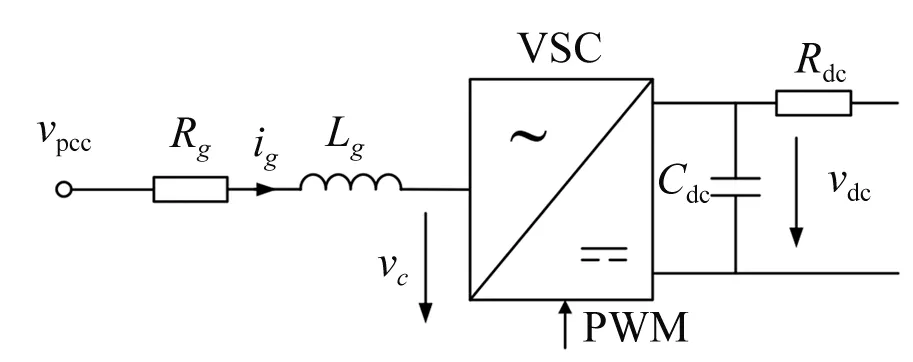
图1 VSC换流系统等效拓扑图

根据图1可以写出时域下开关模型，如式(7)所示[8]。

(7)

式中:swx(x=A,B,C)为变换器的开关函数。将式(7)转变成谐波域模型，如式(8)所示。

(8)

式中：

X=[ΔIgAΔIgBΔIgCΔvdc]T

U=[ΔVpccAΔVpccBΔVpccCΔSWAΔSWBΔSWC]T

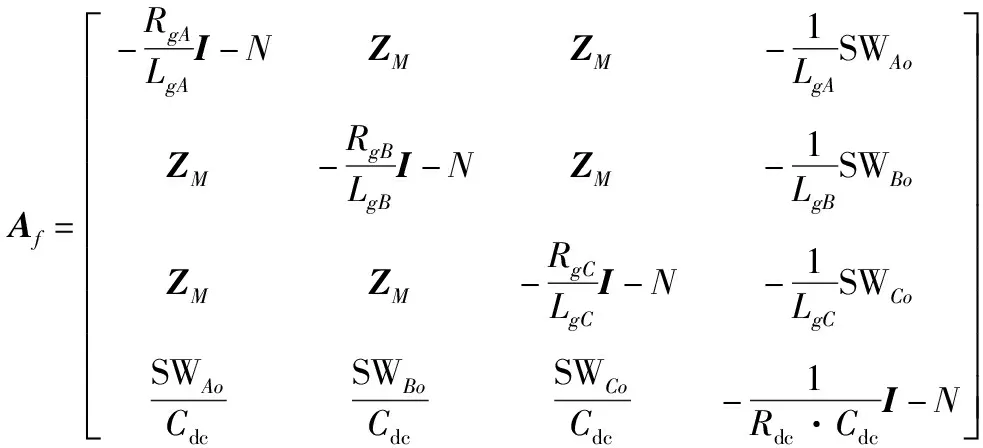
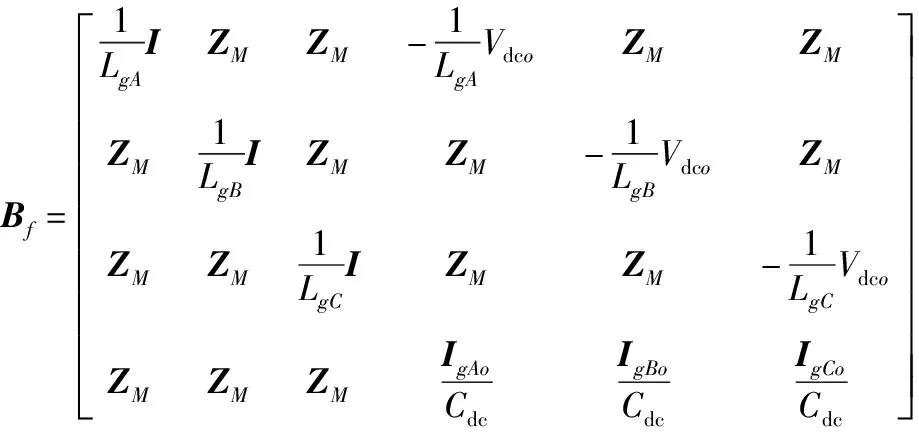
式中：N=[…,-jω0I,0,-jω0I,…]；I为单位矩阵;ZM为零矩阵;SWx为由开关函数傅里叶系数组成的拓普利兹矩阵；“Δ”为变量的小信号量；下标“o”为变量的稳态量。

2.2 VSC-HSS模型验证

在MATLAB中计算VSC换流接口HSS模型，并在PLECS仿真平台搭建换流器模型，Lg取6 mH，Rg取0.1 Ω，Cdc取450 μF，Rdc取160 Ω，线电压380 V含4 V的5次谐波畸变，时域波形及各次谐波含量如图2所示。图2显示HSS模型无论交流侧电流波形还是直流电压波形，和仿真结果具有高吻合度。考虑到MATLAB计算误差及傅里叶变换时的频谱泄露，可以认为本文建立的VSC-HSS模型基本准确。

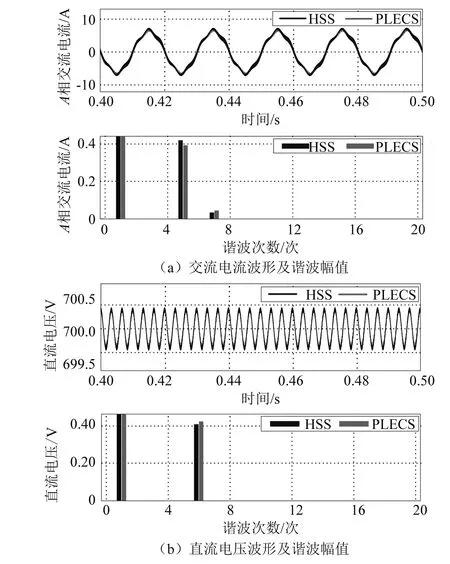
图2 VSC-HSS模型计算结果与仿真验证

3 基于VSC-HSS模型谐波特性分析

3.1 谐波传递函数及耦合导纳

为了研究各谐波之间的耦合特性，需建立各频次之间的谐波传递函数来分析。

根据谐波状态空间理论，由式(8)得到谐波传递函数表达式为：

H(s)=C[sI-(A-N)]-1B+D

(9)

式中:A、B、C、D分别为h维的状态、输入、输出以及关联矩阵；N为h维的对角矩阵。

式(9)中令s=0得到各频次之间的耦合导纳如图3所示。图3给出了-7次～+7次谐波的耦合导纳分布。

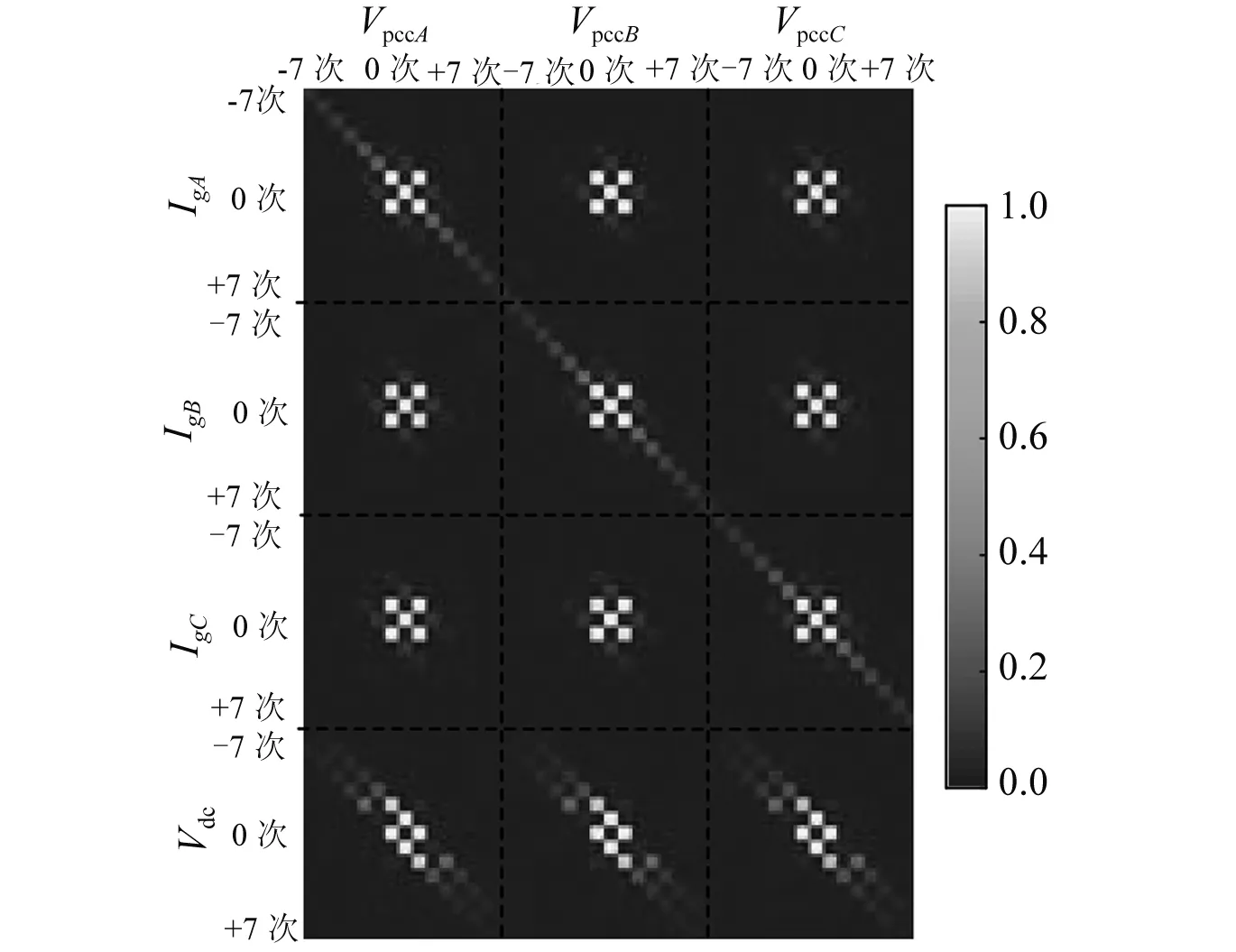
图3 耦合导纳分布图(-7次～+7次)

图4为包含了谐波幅值地耦合导纳三维图，交流电压各频次的输入会产生次频率的直流电压耦合导纳，随着输入谐波次数的升高，交流谐波对直流侧谐波的影响会变小。

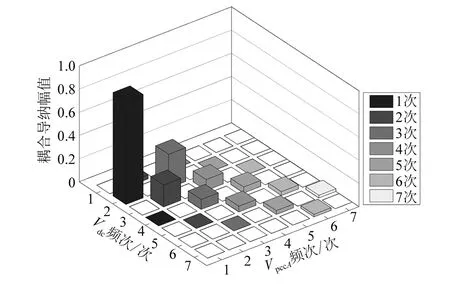
图4 VpccA/Vdc耦合导纳幅值图

图5为VSC换流接口中输入5次谐波的电压时，直流电压4次、6次谐波的耦合导纳幅值随电感值变化的柱状图。随着电感逐渐增加，4次、6次谐波均有小幅度的下降，而低次谐波的幅值始终高于高次。

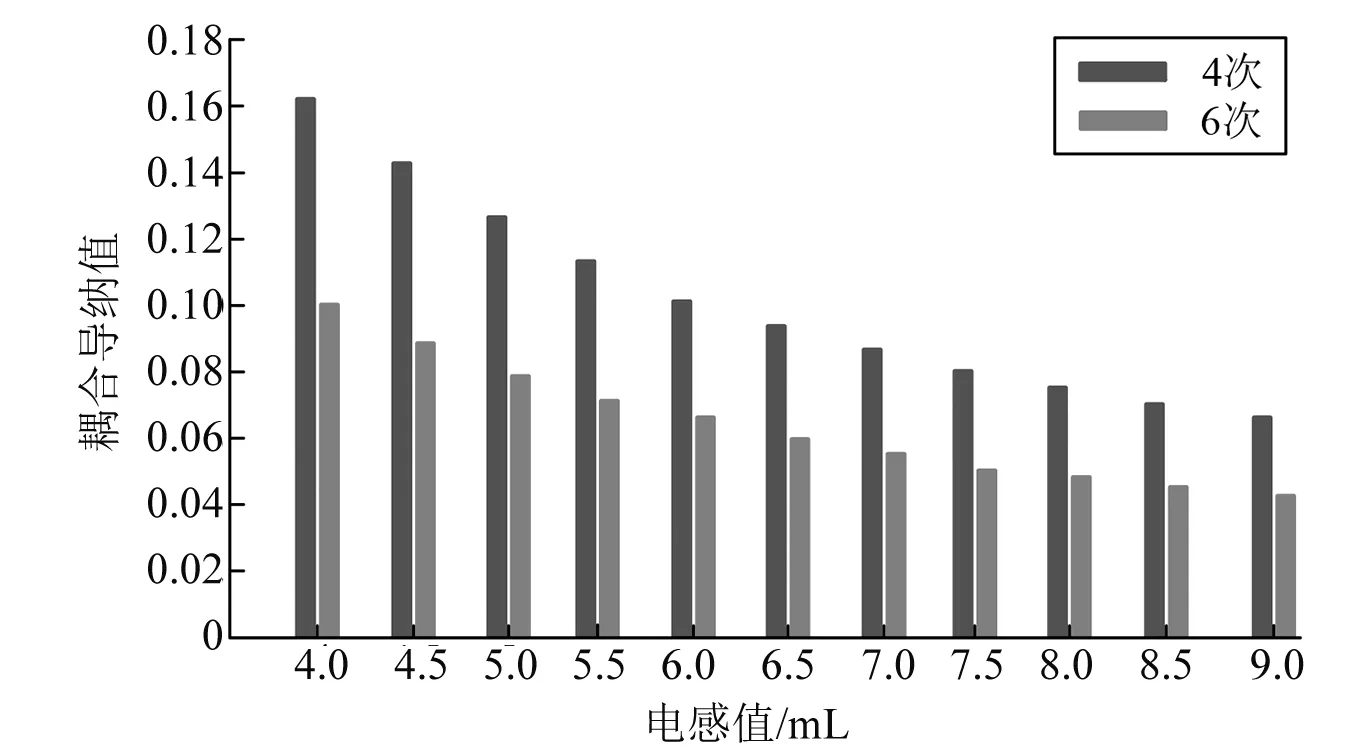
图5 交流侧电感变化时直流电压耦合导纳幅值图

3.2 稳态谐波耦合分析

图6(a)为VSC换流接口交流侧仅A相含有10 V的5次谐波扰动时交流电流及直流电压对应的幅值。图中:A相电流3次、5次、7次耦合谐波幅值分别约为0.2 A、1.2 A、0.1 A;B、C相电流3次、5次、7次耦合谐波幅值分别约为0.2 A、0.6 A、0.1 A。直流侧电压4次、6次耦合导纳幅值约为1.5 V，0.5 V。图6(b)为VSC换流接口三相含5次谐波(10 V)。

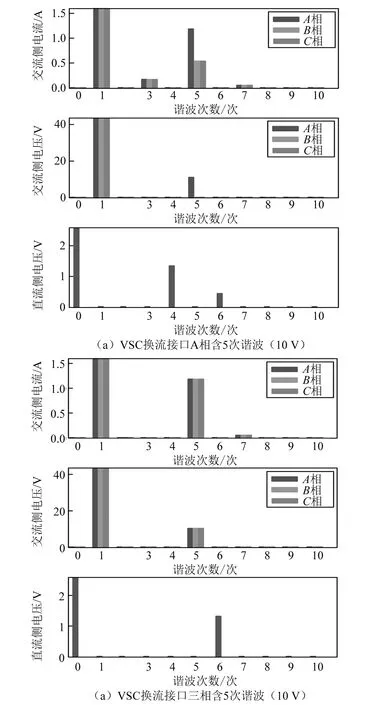
图6 交流侧和直流侧各谐波次数电压电流幅值

图7为耦合导纳分布图中A相、B相、C相的+5次谐波输入对应的三相电流及直流电压输出耦合导纳幅值。各相电流及电压输出的耦合谐波为输入谐波与对应耦合导纳相乘后叠加。如IgA的+5次谐波输出值为：A相+5次输入谐波耦合导纳(0.12)×5 V+B相+5次输入谐波耦合导纳(0.005)×2.5 V+C相+5次输入谐波耦合导纳(0.005)×2.5 V=0.625 A。正负序幅值相等，最终输出+5次谐波为1.25 A，与仿真结果一致，其余谐波耦合幅值都可通过上述方法计算而得。当输入含10 V对称的+5次谐波时，三相中三次谐波因系统结构相互抵消，对应直流电压+4次耦合谐波消失，如图6(b)所示。

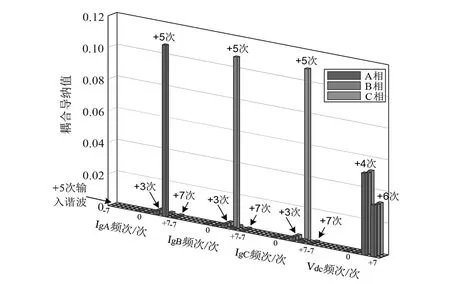
图7 VSC换流接口三相+5次输入谐波耦合导纳幅值

4 结束语

本文建立了稳态运行下的VSC-HSS模型，计算结果得到的时域波形及频域谐波含量与PLECS仿真结果一致。基于VSC-HSS推导的谐波传递函数矩阵得到谐波的耦合导纳。随着谐波次数的增高，谐波耦合导纳减小；随着网侧滤波电感值变大，谐波的耦合导纳幅值会降低。网侧含有不平衡谐波和平衡谐波时，变换器输出交流电流和直流电压的谐波耦合与耦合导纳分布一致。本文VSC-HSS建模方法及谐波特性分析可推广到其他电力电子变换器中。