高耗能企业的用电能效分析

朱群波，郝思鹏

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

对企业进行合理有效的能效评估不仅可以帮助企业掌握能效水平、改进生产工序、降低电能损耗以及减少生产成本，还可以为相关部门制定行业标准提供有力依据。目前，国内已有学者对工业用户的能效评估展开研究。文献[1]通过K-means聚类分析将企业分为5类，对各个生产单元的生产、照明及空调系统进行评估，最后全面考虑各单元影响因素，得出综合评估结果。文献[2]针对中小企业，从技术、经济和管理能效三方面建立指标体系，但其一、二级指标权重矩阵的得出具有很强的主观性，存在较大误差。文献[3]依据熵权法和专家打分法确定权重，定义企业的节能减排效果到理想点和负理想点的偏离度，并将其作为评估标准，得出企业的评估结果。

本文在已有研究成果的基础上，建立了高耗能企业能效水平多层指标评估体系。考虑企业能效状态可能对经济性、运行参数和电能污染等三方面造成的影响，将AHP和熵权法结合使用，得到各指标权重及综合权重矩阵[4-5]。依据指标特性进行分类，应用不同类型指标对应的隶属函数和评语集对应分数求得指标评分值，再将分值与权重逐一对应，构成合理有效的评估体系。最后，根据评估结果,分析企业能效水平和可能的改进方案。

1 评估体系的建立

根据实际采集数据的便利性和可能性，将数据归为三类。首先，企业的利润和用电量大小等数据必然是评估的重点，因此建立生产信息指标；其次，将企业生产的效率和可靠性因素建立为电能信息；最后将体现企业迎合节能减排要求的因素建立为用电管理信息，指标体系如图1所示。

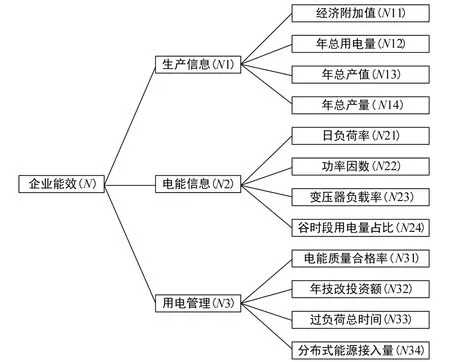
图1 企业能效评估指标体系

2 权重计算方法

高耗能企业的能效状态会对经济性、运行参数和电能污染三方面产生影响，将具有主观特性的AHP法和客观特性的熵权修正法结合，计算各个指标的权重。

2.1 层次分析

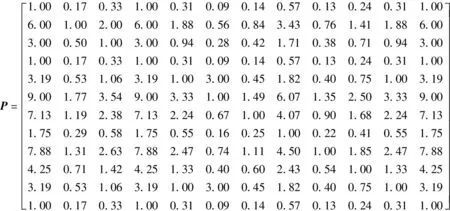
将指标体系中各指标按照重要度进行相互比较，构建出判断矩阵P。将经济性、运行参数和电能污染三个方面的受影响程度记为X、Y、Z。根据实际生产经验，令X∶Y∶Z=0.4∶0.3∶0.3,同时有X+Y+Z=1。

1)经济性受影响程度

将经济性各指标受企业能效水平的影响视作1，则其各项指标间的受影响之比为α1∶β1∶γ1∶δ1∶ε1，设定两两指标间的比值相同，结果如表1所示。

表1 经济性指标与企业评估指标对应关系

2)运行参数受影响程度

将运行参数各指标受企业能效水平的影响视作1，则其各项指标间的受影响之比为α2∶β2∶γ2∶δ2，设定两两指标间的比值相同，结果如表2所示。

表2 运行参数指标与企业评估指标对应关系

3)电能污染受影响程度

将电能污染各指标受企业能效水平的影响视作1，则其各项指标的受影响之比为α3∶β3∶γ3∶δ3，设定两两指标间的比值相同，结果如表3所示。

表3 电能污染指标与企业评估指标对应关系

将表1～表3中各指标对应的总重要度整理排序，结果如表4所示。

表4 二级指标总重要度汇总表

将各个参数设定值代入表4，得到总重要度矩阵Z=[1/50 3/25 3/50 1/50 51/800 17/80 57/400 7/200 63/400 17/200 51/800 1/50]。用0～9来反映两指标间的重要度比值，数值越大表明第m个指标相对第n个指标的重要程度越高，比值不在0～9内时做适当调整。

使用特征值法，求得λmax=13.262 7和权重向量Q=0.01×[1.85 11.14 5.57 1.85 9.80 19.07 13.26 3.25 14.64 7.90 9.80 1.85]。将λmax代入CI=(λmax-n)/(n-1)，CR=CI/RI，可知判断矩阵P满足一致性检验。

2.2 熵权法

将AHP与熵权法结合，可消除部分主观误差。熵权法步骤如下：

(1)将判断矩阵P行归一化得矩阵R。

(2)计算各指标熵值得到熵值矩阵S。

(1)

(2)

S=[s1s2s3…sn]

求得熵值矩阵S=0.01×[7.77 7.79 7.79 7.77 10.66 6.49 7.77 7.79 8.87 8.87 10.66 7.77]。

(3)计算综合权重矩阵T。

(3)

T=[t1t2t3…tn]

则有T=[0.02 0.1 0.05 0.02 0.13 0.15 0.12 0.03 0.16 0.08 0.13 0.02]。

3 指标的模糊评分

评语集通过设定多个等级区分指标的优劣，隶属函数通过分段函数计算出指标的评分，将分值与评语对应就可以掌握指标水平。

3.1 评语集的设定

使用{好，中，差}作为评估企业能效水平的评语集，三个等级的评语对应的隶属函数分别为η1、η2和η3。

3.2 隶属函数的选定

本文选用三角型隶属函数，根据各指标的期望数值，将其划分为趋大型、趋小型和区间型,其中:N11、N13、N14、N21、N22、N24、N31、N32、N34属于趋大型；N12、N33为趋小型；N23为区间型。

1)区间型隶属函数

令b32、b31为区间型指标的阈值上下限，b22、b12为区间型指标期望值的上下限，并令b22为b12和b32的中间值，b21为b31和b11的中间值。区间型指标的隶属函数式如式(4)～式(6)所示，隶属函数图如图2所示。

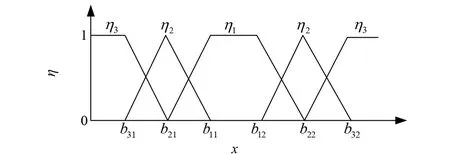
图2 中间型隶属函数图

(4)

(5)

(6)

2)趋大型、趋小型隶属函数

趋大型和趋小型指标的运算机理与区间型相似，不再赘述。

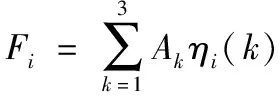
F=[F1F2F3…Fn]

4 算例分析

本文采集盐城市某机械制造企业2019年度数据，计算得到评分矩阵F=[83 85 85 84 79 93 87 89 93 74 91 65]，利用式F总=TFT计算得到F总=87.35。将二级指标评分矩阵F与一级指标评分和总评分整理，具体如表5所示。

表5 各级指标评分值

令F总的评语集{好，中，差}对应评分区间依次为85～100、70～85、70分以下，则该机械制造企业的能效水平对应于评语“好”，这表明该企业的生产能效处于较为理想的状态。分析各二级指标:A21评分较低，表明企业未能合理安排生产工序，造成了某些时段负荷过大，使得日负荷率未能达到工业企业国家标准，且可能造成供电质量下降；A32评分较低，表明企业每年用于技术升级改造的资金较少，不利于提升自身节能降耗能力，将会使生产能耗水平高于同类型企业，进一步压缩了利润空间；A34评分较低说明企业在厂区内部投入的新能源发电模块较少，该企业可以适当增加光伏等类型的发电装置，已降低用电成本，提升能效水平。

5 结束语

本文着眼于企业生产能效对经济性、运行参数和电能污染三方面的影响，计算出各指标的综合权重。根据模糊评分理论，计算出模糊评分并综合形成评分矩阵，最后与权重结合计算出总评分F总。所提方法为企业节能减排、提高自身生产效能提供了技术支持，具有较好的实用性。