QoS-Aware Power Allocation Scheme for Relay Satellite Networks

Jin’ao Yu, Xiaogang Tang, Shibing Zhu, Haopeng Sun,Lunxin Zhong, Guangyu Yang

Abstract: This paper investigated a QoS-aware power allocation for relay satellite networks. For the given QoS requirements, we analyzed the signal model of relay transmission and formulated the power minimization problem which is non-convex and difficult to solve. To find the optimal solution to the considered problem, we first analyzed the optimization problem and equivalently turn it into a convex optimization problem. Then, we provided a Lagrangian dual-based method to obtain the closed-form of the power allocation and provided an iterative algorithm to the optimal solution.Moreover, we also extended the results to the cooperative transmission mode. Finally, simulation results were provided to verify the superiority of the proposed algorithm.

Keywords: power allocation; relay satellite network; quality of service; cooperative transmission

1 Introduction

Satellite networks operating as the supplement to ground networks have received extensive attention in recent years[1-3]. Especially, its extensive coverage is very appropriate for communication in remote areas as well as at sea. However, the shortcoming of satellite networks is that the resource is very limited [4-6]. Such as power, frequency, orbit, antenna, and etc. There are some works paying attention to the power allocation of satellite to improve the system capacity, the data rate, and other performances[7]. For example, the authors in [8], studied the energy-efficient power allocation problem of satellite network by using the fraction at optimization frame work.Moreover, the authors in [9] investigated the power allocation method for multibeam satellite network to maximize the system energy efficiency. By using the game theory, the power allocation method was achieved from the game perspective by balancing the interference and cost in[10]. Through solving the Nash equilibrium, the total system data rates can be improved obviously. However, the works in [8-10] take into account the whole system performance but ignore the cost of power. Due to the difficulty of satellite charging, the power consumption is a key point to the satellite system[11-13].

For the case of indirect transmission between satellites and users, relay-assisted satellite network is necessary. For the current, there are some works to analyze the relay selection schemes and power allocation problem. For example, in [14], the authors provided the relay selection method from the view of the outage probability and showed the effect of system parameters on the outage probability. In [6], the authors provided the power allocation method for maximizing link capacity and mainly studied the link matching problem or routing problem. The loss probability and delay performances were analyzed for relay satellite network through the queuing theory in [15]. In [16], the authors considered the achievable rate maximization problem for a hybrid satellite-terrestrial network and obtained the optimal power allocation method by analyzing the KKT conditions.

In this paper, we paid more attention to power minimization problem for relay satellite network. The main contributions include four point. 1) We considered the power cost problem of given QoS requirement. 2) The efficient and low complexity optimal power allocation algorithm was proposed. 3) Both relay transmission mode and cooperative transmission mode were considered. 4) By using the proposed algorithm, the power consumption can be decreased obviously.

2 System Model and Problem Formulation

As illustrated in Fig. 1, the scenario considered in this paper is a multi-source single relay system model consisting of multiple source satellites M ={s1,s2,··· ,sM}, one relay satellite R, and one ground station G. Instead of the direct communication between source satellites and ground station, the source satellites transmit the signals to ground station with the help of relay satellite.With the given quality of service (QoS) requirements, we consider the power minimization problem based on the amplify-and-forward (AF) protocol. According to the AF protocol, the source satellites first send the signals to relay satellite,and then the relay satellite amplifies the signals and forwards them to ground station. Here, the amplification factor is related to the QoS requirements, and thus, a tradeoff of transmit power between the source satellites and the relay satellite should be considered. Moreover, there is also a conflict among the accessed source satellites due to the limit of total power of relay satellite.

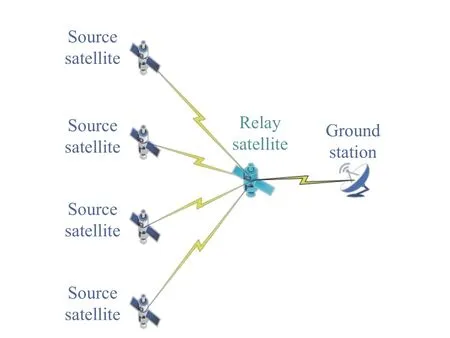
Fig. 1 The multi-source single relay satellite network model

To further analyze the effect of power, we first provide the signal model on the basis of AF protocol. The transmission of the signal is divided into two stages. In the first stage, the signal is transmitted by inter-satellite link between the source satellite siand relay satellite. The received signal by relay satellite is expressed as

where qiis the power of relay satellite for the link between relay satellite and source satellite s.

iis the total gain similar toandis the channel gain. As a result, the output signal noise ratio (SNR) of ground station can be expressed as

Accordingly, the following power minimization problem can be formulated as

where Rminis the minimum data rate requirements of the links. Qmaxis the maximum transmission power of the relay satellite and Pmaxis the maximum transmission power of the source satellite.

In the constraints above, C1 ensures that the QoS of each link is satisfied. C2 ensures that the transmission power of the relay satellite is not more than Qmax. C3 ensures that transmission power of the source satellite is not more than Pmax. Moreover, the proposed optimization problem is a non-convex problem because the data rate function is not convex. It is difficult to solve such a problem. Usually, some approximation methods are applied to translate it to a convex problem. However, the optimality of the solution is not guaranteed. Hence, in the following section, we aim to find out the optimal solution through an efficient method.

3 Optimal Power Allocation Algorithm

In this section, we first analyze the constraints in optimization problem and turn it into a convex optimization problem. Then, we further proposed an iteratively power allocation algorithm using the Lagrangian dual method. For the proposed optimization problem, the main difficulty is the constraint C1. To deal with it, we find out the fact that the constraint C1 must be satisfied with the equality because the data rate is a increasing function about piand qi. This can be verified by the derivative of Ri. Then, we try to obtain the relation between piand qi. To show it,we provide the following theorem.

Theorem 1 To satisfied the constraint C1,the relationship between piand qican be expressed as

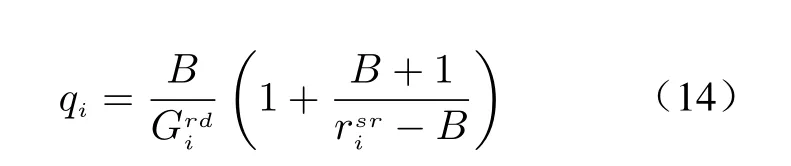
The proof has been completed. Substituting Eq.(14) into the original optimization problem(7), we can rewrite the optimization problem (7)as follows.

Notice that the above optimization problem is a convex optimization problem because all the function is convex function. The fact can be verified by the derivatives. To solve the convex optimization problem, Lagrangian dual method is the efficient algorithm for the moment. The lagrange function of the problem (15) is given by

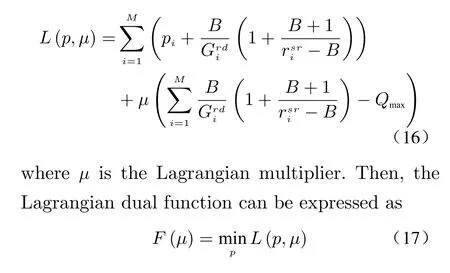
The Lagrange duality problem is equivalent to

Then, to solve the optimal power allocation,we take the derivation of Lagrange function (16)with the following formula.

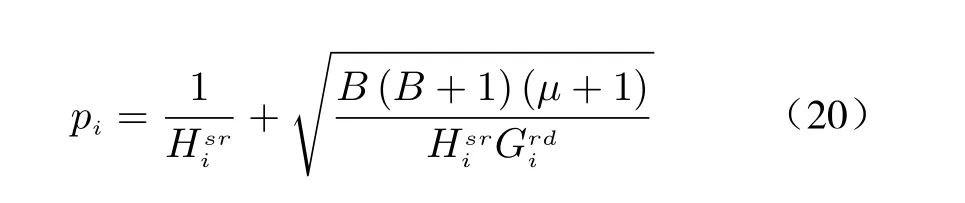
By considering the constraint C3, the closedform of qican be written as

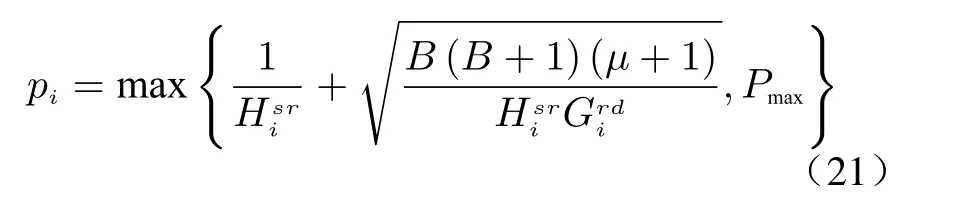
For the Lagrangian multiplier μ, a gradient descent method can be applied to update it. The specific step is listed as

Then, we can design the corresponding iterative algorithm according to Eqs.(21)-(23). The specific algorithm can be found out in Algorithm 1.

Algorithm 1: Optimal power allocation algorithm based on Lagrangian dual method.Input: the convergence threshold and the maximum number of iterations.Output: the optimal power allocation.Initialize the power and Lagrangian multiplier.t=1:tmax for do i=1:M for do Update the power allocation according to Eq. (21).Update the Lagrangian multiplier according to Eq.(22).|ϖt+1-ϖt|≤ε if then Break the “for” loop.end if end for end for

4 Optimal Power Allocation Algorithm of Cooperative Transmission

In the previous section, we have provided the optimal power allocation algorithm for relay transmission mode. However, in some cases, the source satellite may be visible to the ground station. In this case, the cooperative transmission of the relay satellite and the source satellite is better than the directly relay transmission. In this section,we aim to expand our results about the optimal power allocation algorithm of relay transmission to the case of cooperative transmission. The results are similar.

Before introducing the algorithm, we first provide the received signal model of ground station. We can know that in the first stage, the received signal by relay satellite is. If the source satellite is visible to the ground station, the received signal by ground station by direct transmission can be expressed as

With the application of the maximal ratio combiner, the SNR in ground station is calculated as

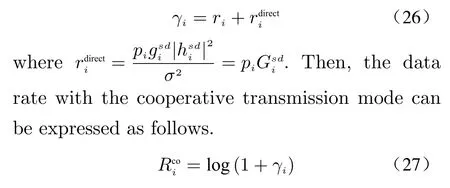
Then, the optimization problem of cooperative transmission mode is written as

Similar to Theorem 1, we can obtain the corresponding relation between piand qias shown in Theorem 2.

Theorem 2 To satisfied the constraint C1,the relation between piand qican be expressed as

Then, we can obtain

Then,

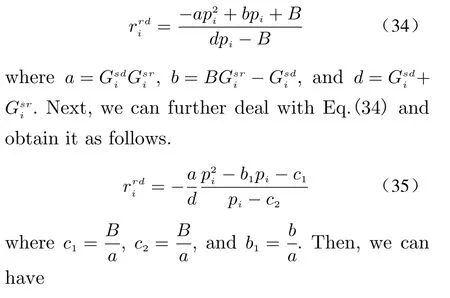
The proof has been achieved.

For convenience, we define

Then, the optimization problem (28) can be rewritten as

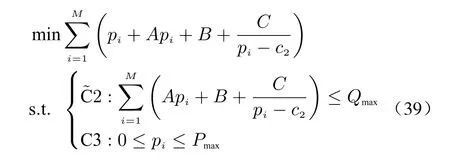
To show the optimization problem above is a convex optimization problem, we have to prove that the parameter is more than 0. To show it,we provide the Theorem 3 as follows.

The Lagrange duality problem can be written as

Then, by taking the derivation of Lagrange function (42), we can further solve the optimal power allocation. The derivation of Lagrange function (42) is

The step size ω′is set according to the requirement (23). Then, the optimal power allocation algorithm can be designed based on (47）（48）. To provide more details, we provide Algorithm 2.

Algorithm 2: Optimal power allocation algorithm for cooperative transmission.Input: the convergence threshold and the maximum number of iterations.Output: the optimal power allocation.Initialize the power and Lagrangian multiplier.t=1:tmax for do i=1:M for do Update the power allocation according to Eq. (47).Update the Lagrangian multiplier according to Eq.(48).|ϖt+1-ϖt|≤ε if then Break the “for” loop.end if end for end for

5 Simulation Results

In this section, we provide the simulation results to verify the effectiveness of proposed algorithms.To do the simulation, we need to provide some detailed parameter. Specifically, we assume that the carrier frequency of inter-link between relay satellite and source satellite is Ku band. And, the carrier frequency of satellite-ground link is Ka band. The received noise power at ground station is -174 dbm/Hz. The Boltzmann constant is 1.38×10-23. In addition, the transmitting antenna gain and receiving antenna gain of satellite are 20 dB. The receiving antenna gain of ground station is 30 dB. The number of satellites is varying in this section.

To verify the superiority of the proposed algorithms, we compared the proposed Algorithm 1 with the following benchmark, i.e., fixed power allocation. For fixed power allocation algorithm,the power of the relay satellite is uniformly allocated to each link corresponding to each source satellite.

Fig. 2 shows how the total power varies with the data rate. As we can see, the total power increases with the increase of data rate requirement. This is because both relay satellite and source satellite need to increase the transmitted power to meet the data rate requirement. In addition, compared with fixed power allocation algorithm, there is an obvious improvement in terms of the performance. For example, when the data rate requirement is 0.1 bps/Hz, the total power consumption decreases 83.4% by using the proposed algorithm.

Fig. 3 shows the varying of total power with the number of accessed satellite increasing. We can see that the total power also increases with the number of accessed satellite increasing. This is because the total data rate requirements increase with the number of link growing. By using the proposed algorithm, the power consumption can be decreased obviously.

Fig. 3 The total power versus the number of accessed satellite

Fig. 4 shows the convergence of the algorithm. According to the Lagrange duality theory, the proposed algorithm finally converges to optimal solution. It can be seen that the objective function value converges to optimal solution after 7 iterations.

Fig. 4 The convergence of the algorithm

6 Conclusion

This paper studied the optimal power allocation method for relay satellite networks. To find out the optimal, we first analyzed the relay transmission mode and provided an efficient iterative algorithm with the derived closed-form of power allocation. Then we, extended the corresponding results to more complex model, i.e., cooperative transmission mode. To verify the superiority of the proposed method, we have compared the proposed algorithm with the fixed power allocation method. By simulation results, it can be seen that there is an obvious decrease in terms of the power consumption.