基于迭代的虚拟视图合成算法实现

刘伟民

（四川大学计算机学院，成都610065）

0 引言

近年来，随着人们生活水平的不断提高，对视频播放系统的需求也在不断增加。传统的视频播放系统仅能够播放固定视点下单一视线方向捕获的画面，导致用户观看场景的自由度不高，体验感下降。为了提升用户的体验，许多学者对此进行了大量研究。在虚拟现实领域，可以通过VR 眼镜实现360°的场景观看，并支持用户移动等交互。但是由于硬件计算性能的限制，目前无法实时渲染高质量的画面。NVDIA 推出了VR 视频解码框架，通过实时解码全景高清视频，能够支持用户360°的自由观看场景。然而，该方案限制了用户的移动，仅能够在固定视点观看周围场景。为了允许用户自由观看场景并且达到实时渲染的目的，Fujii T 等人[1]提出了自由视点电视系统（Free Viewpoint Television，FTV）概念，使得这一需求成为可能。

FTV 系统主要采用基于深度图像的渲染技术（Depth Image Based Render，DIBR）[2]，将周围已经捕获的图像信息映射到虚拟视点处，得到虚拟视点的图像信息。DIBR 技术无需进行场景的几何建模，也无需计算复杂的光照信息，能够满足实时渲染的需求[3]。

然而，基于深度的图像渲染技术中存在很多问题，例如空洞、伪影、重叠等[4]，影响合成图像的质量。空洞问题主要分为两类：采样不足造成的细小空洞以及信息缺失导致的空洞。细小空洞又称为裂纹，如图1（a）所示。造成该现象的主要原因是映射过程中，像素映射到非整数像素上，需要进行取整操作，从而造成舍入误差，采样率不足[5]。较大的空洞如图1（b）所示，主要由于虚拟视点视角发生变化，导致参考图像中前景物体后的背景物体重新暴露在虚拟视点下，而参考图像无法提供对应的背景信息。伪影现象如图1（c）所示，背景物体上出现前景物体的部分信息，造成图像失真。造成伪影的主要原因是物体轮廓处的深度值与颜色值不匹配造成的，通常采用深度图边缘预处理解决[6]。在进行视图合成时，参考图像的多个像素可能映射到虚拟视点的同一像素位置上，造成如图1（d）所示的前景颜色被背景颜色覆盖的情况，这种现象称为重叠现象[7]。Fehn 等人[8]利用控制绘制顺序的方式解决重叠问题，但是该方案不适用于GPU 并行框架，Greene 等人[9]提出Z-buffer 策略，利用深度过滤掉背景物体，可以很好地支持并行计算结构。

为了解决空洞问题，本文提出一种基于GPU 加速的逆向映射算法。该算法基于不动点迭代的思想，利用移动向量构建不动点迭代关系式，能够很好地避免细小空洞的产生。同时利用两幅参考图像合成虚拟视图，能够有效地减少空洞的产生。最后针对存在的空洞，采用基于深度引导的空洞修复方式进行填充。本文使用OpenGL 的计算着色器实现并行计算，并验证了算法的有效性。

图1 DIBR技术中存在的问题

1 虚拟视图合成算法概述

1.1 像素映射方式

在视图合成算法中，根据像素映射方式不同，可以将DIBR 技术分为前向映射方式与逆向映射方式。前向映射方式如图2（a）所示，使用3D-Warping 方程将参考图像的每一个像素映射到虚拟视图上。其中(x',y')可能存在浮点数情况，需要进行像素取整或者采用Splatting 算法[10]进行处理。像素取整会造成虚拟视图中出现大量“裂纹”，而Splatting 算法需要对映射的点做加权计算，不利于并行计算。逆向映射方式如图2（b）所示，利用逆向映射函数T-1( )x,y将虚拟视图上的每一个像素映射到参考图像上，通过双线性插值或者三线性插值等方式采样图像，可以得到虚拟视点的图像信息。相较于前向映射方式，逆向映射方式能够更好地支持GPU 并行计算，而且可以避免“裂纹”现象的出现，但是需要找到对应的逆向映射关系。

1.2 基于原子的逆向DIBR算法

当多个参考图像上的像素点同时投影到虚拟视图的同一位置上时，会出现写入数据竞争的问题，为了解决这个问题，可以采用原子写入的思想。基于原子的逆向DIBR 算法首先通过前向映射方式将像素点投影到虚拟视图上，通过舍入取整得到要写入的像素位置，然后利用深度信息进行原子最小写入，即将深度最小的点写入到GPU 内存中。此时会得到带有裂纹的深度图，对深度图进行滤波处理能够得到虚拟相机的粗略深度图。之后根据虚拟相机的深度图进行重投影，利用投影到参考相机的点进行采样，最终能够得到虚拟视图的信息。

基于原子的DIBR 算法能够适用并行计算框架，可以快速得到虚拟视点的图像信息。但是，对带有裂纹的深度图进行滤波可能会造成图像失真现象，影响合成的图像质量。本文提出一种基于迭代的DIBR 算法，无需对深度图进行滤波，可以得到高质量的虚拟视图，接下来对基于迭代的DIBR 算法进行详细的阐述。

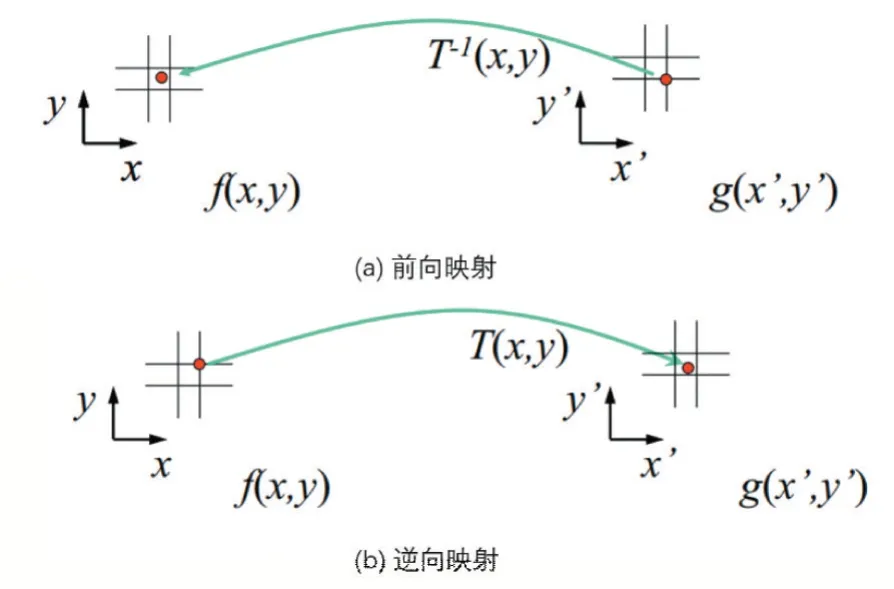
图2 前向映射与逆向映射示意图

2 基于迭代的DIBR算法

2.1 不动点迭代思想

本文采用的基本思想是不动点迭代思想。不动点迭代是求解复杂方程f(x)=0 的重要方法。如图3 所示，假设要求解方程f(x)=x-g(x)，不动点迭代思想会将函数f(x)分解成两个函数y=x与y=g(x)。其中两个函数的交点x*就称作不动点，也是函数f(x)的零点。任取一点x0，根据公式（1）进行迭代计算，若迭代序列收敛到g(x)的不动点，即，则不动点迭代收敛，否则不动点迭代发散。

2.2 二维图像的不动点迭代

对于二维图像而言，虚拟视图上的点p与参考图像上的点q存在如公式（2）所示的对应关系：

其中，V(q)表示q点移动到p点的移动向量。

在基于DIBR 的视图合成算法中，移动向量可以根据深度快速计算得到。已知参考相机的内外参矩阵Mr以及虚拟相机的内外参矩阵Mv，可通过公式（3）计算得到参考图像的点q投影到虚拟图像上点p' 的对应位置：

然后利用公式（4）得到每个像素映射的移动向量，得到一张移动向量图。

根据公式（2）的对应关系，我们可以构建不动点迭代关系式：

其中，在逆向映射过程中，p为已知信息，表示虚拟视图的每个像素位置。V(qi)为qi位置处对应的移动向量。w(qi)表示一次迭代后的结果，将该结果赋值给qi+1进行进一步的迭代。

图像迭代过程中，前一次迭代结果qi-1与当前迭代结果qi之间的距离小于一个像素大小时，迭代可看作收敛。当迭代收敛时，可通过得到的迭代结果采样得到对应的颜色值。

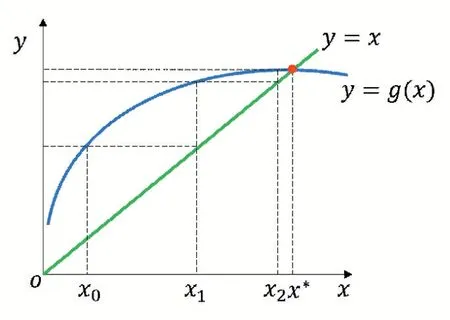
图3 不动点迭代示意图

2.3 局部包围盒策略

在进行虚拟视图合成时，会出现重叠现象，即在本文算法中，公式（5）可能存在多个迭代收敛的结果。引起该问题的主要因素是初始点的选择。针对此问题，本文采取选择多个初始点进行迭代的策略：当多个初始点进行迭代时，若存在多个收敛结果，则对比每个迭代收敛结果的深度，选择深度最小的点作为最终的采样结果，从而避免重叠现象。

当增加选择的初始点数目时，图像质量提升，但是同时增加了计算开销，导致性能降低。为了降低开销，增加系统的运行效率，本文采用局部包围盒策略对初始点的选择范围做了进一步缩小，能够在保证收敛的情况下，减少初始点的选择数目。

局部包围盒策略采用的主要思想是利用移动向量在局部的最大值，构成矩形包围盒，由于采用的是最大值，所以在该包围盒中一定存在收敛的点，从而保证了迭代收敛。如图4 所示，具体步骤如下：当计算移动向量时，同时计算该移动向量沿着图像坐标系X-Y 的分量。若当前分量大于局部区域存储的最大分量，则将其进行替换。最终划分的每个区域都会存储最大的局部包围盒，在该包围盒下进行初始点的选择，能够减少计算开销。

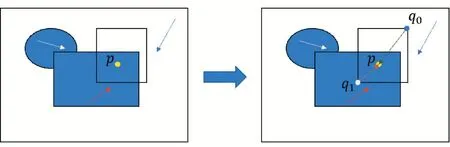
图4 局部包围盒示意图

3 算法流程

本文算法通过C++与OpenGL 进行计算与绘制。算法流程如图5 所示，首先通过计算着色器将参考图像的每个像素根据深度重投影到虚拟视图上，计算像素的移动向量以及对应的局部包围盒，并通过可写入的Image2D 图像纹理进行存储。之后再利用计算着色器进行第二遍并行计算，读取局部包围盒的数据，随机初始化N个点，进行迭代计算，当迭代次数大于规定次数时，迭代不收敛，舍弃结果。当迭代收敛时，将其存入到候选点集中，最后通过对投影的深度进行排序，选择最小的深度作为最终的采样坐标进行采样。通过前两遍的计算着色器已经能够得到最终合成的图像了，第三遍为绘制渲染，通过渲染屏幕大小的一张二维网格并对其着色，最终呈现出合成的图像。由于本文采用的是两个参考视点进行虚拟视点的合成，最终合成的图像空洞信息较少，但是依然不能避免空洞的出现。本文在渲染绘制遍时对这些较少的空洞进行修复，主要利用已知的深度信息进行前景与背景物体的识别，利用背景物体的颜色进行填充能够得到较好的结果。

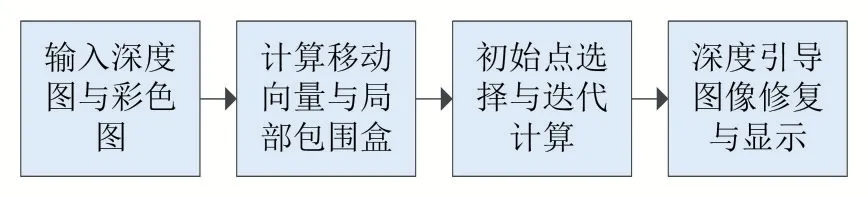
图5 算法流程图

4 实验结果

本节的实验设备信息如表1 所示。

表1 实验设备信息表

图6 展示了本次算法输入的两张参考图像以及对应的深度图像。

图6 输入的左右参考图像与深度图像

图7展示了基于原子的DIBR 算法、本文基于迭代的DIBR 算法以及Ground Truth 参照图，其中基于原子的DIBR 算法出现了明显的失真情况，造成该失真情况的主要原因是投影时取整造成的裂纹被背景物体填充。本文利用峰值信噪比PSNR 以及结构相似性SSIM进行测试，结果如表2 所示。

图7 实验结果对比

表2 实验设备信息表

5 结语

本文给出了基于迭代的DIBR 算法的基本思想，并利用C++与OpenGL 实现并行计算架构。该算法比基于原子的DIBR 算法在PSNR 和SSIM 上有一定提升。但是本文算法需要进行额外的移动向量计算以及多个初始化迭代点的选择，当迭代点数目增多时需要的时间代价十分昂贵。在后续的研究中，会针对初始点的选择进行进一步优化，减少初始点的选择数目以提升算法的运行效率。