基于OpenMP 加速的符号距离场构建算法实现

何康本

（四川大学计算机学院，成都610065）

0 引言

随着图形处理器硬件的高速发展，使得绘制更高质量的图形效果变为可能。然而，目前游戏中的实时绘制的绘制效果仍然和离线渲染的真实效果（Ground-Truth）间较大的差距。近些年来，硬件公司一直通过优化硬件来弥补差距，2020 年NVIDIA 公司在2018 年发布的显卡基础上，进一步优化硬件性能，发布最新光线追踪优化的显卡。然而，光线追踪过程中需要求解渲染方程，其中设计大量的积分计算，想要在游戏中实时实现基于物理的实时全局光照效果仍然需要时间。同时，支持光线追踪显卡价格昂贵，老一代显卡并不支持硬件光线追踪。因此，使用其他渲染方法便成为人们关注的焦点，利用符号距离场进行图形绘制便是其中之一。

利用符号距离场进行场景绘制的应用在近些年来大量增多。早在2013 年，Rougier[1]利用符号距离场实现高质量的2D 文本绘制。在2015 年的Siggraph 大会上，Wright 等人[2]利用符号距离场实现环境光遮蔽（Ambient Occlusion）、软阴影（Soft Shadow）等渲染效果。在2018 年GDC 上，Sebastian[3]介绍符号距离场在游戏《Claybook》中的应用，其只利用符号距离场进行场景的绘制，同时在Wright[2]实现环境光遮蔽（Ambient Occlusion）、软阴影（Soft Shadow）等效果的基础上，进一步提升渲染效果。

符号距离场（Signed Distance Field）能够表示空间中任意一点到最近物体表面的最短距离[4]。其能够对场景的距离信息、物体表面信息进行有效表达。在数学中，其为三维空间映射到一维空间中函数，具体定义为

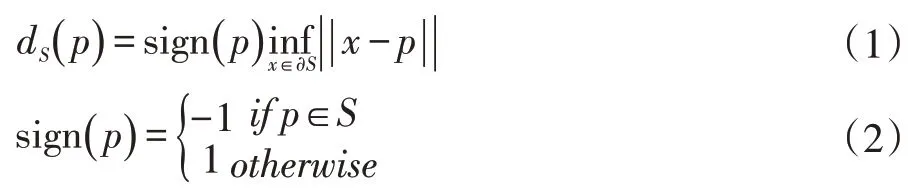
其中S 是构成模型的点，这些点的组成整个物体对象。函数Sign 用以确定点是否在模型内部，若在内部则返回-1，反之为1。

符号距离场实则是符号距离函数的近似，即可完全使用符号距离函数代替符号距离场。然而，在游戏场景中，大多数物体构造往往十分复杂，不具备解析的符号距离函数。故在游戏中，常常通过网格离散化物体，并通过计算网格中心的符号距离值来构造符号距离场，同时将相应的计算值存储在体纹理中，从而方便在渲染时使用。然而上述预计算符号距离场，存在计算量极大，导致计算效率不高及耗时长的问题。

本文将三维模型作为输入，通过OpenMP 库并行加速三维模型符号距离场的生成，进行相关效率对比及通过球体追踪的方式验证符号距离场生成的正确性。

1 算法实现

1.1 算法描述

符号距离场有多种生成方式，其中最主要的两种分别是符号距离函数及网格转换算法。其中第一种方法适用于具有解析符号距离函数的三维图形，如球、正方体等，同时，对于复杂模型，则可利用符号距离函数进行一系列布尔运算，得出相应的符号距离函数。另一种方式是通过距离转换算法，将三维网格模型转化生成符号距离场，该方法可利用OpenMP 进行并行加速。下面，将对上述两种算法概述。

1.2 符号距离函数表示符号距离场

符号距离函数在数学中用于表示点到表面的最近距离，是表示距离场最简单的方式。大部分基本图形都有着解析的符号距离函数，但不同的几何图形的符号距离函数也并不同。模型间的符号距离函数的计算复杂度也有着区别，但都以空间中点的位置坐标作为输入，计算出相应的符号距离值。以球为例，其符号距离函数如公式（3）所示：

其中(x,y,z)表示空间中任意一点位置，(xr,yr,zr)表示球体中心点坐标，r表示球半径。

对于复杂模型而言，其并不具备直接解析的符号距离函数，可通过简单模型的符号距离函数通过布尔运算组合而成，图1 可视化该过程。通过组合运算，并不影响符号距离值计算的正确性。

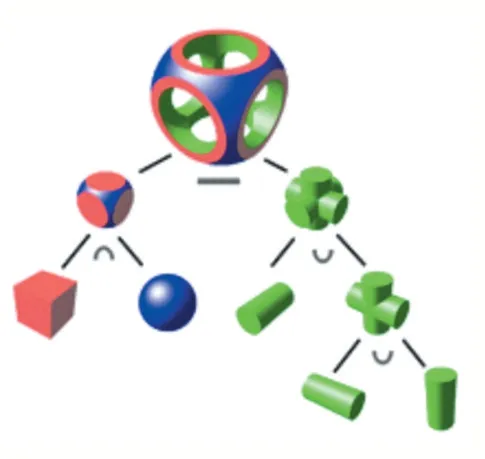
图1 简单图形布尔运算

由于符号距离函数计算复杂度低，可直接在GPU中进行相应计算，能够满足运行时实时计算的需求。同时，其不包含三角网格数据，几乎不占用内存空间，在小型绘制场景中，常常利用符号距离函数进行模型的相应绘制[5]。

1.3 网格转换符号距离场

在游戏场景中，存在许多十分复杂的模型，其并不具备解析的符号距离函数。同时，由于图形处理器定制化的绘制管线，在游戏行业中，往往使用三角网格对物体进行建模表示。对于上述这些物体，无法通过符号距离函数表示符号距离场。为此，可通过距离变换算法将网格模型转化为相应的符号距离场。

在过去的几十年中，提出了各种各样的网格距离变换算法。蛮力法（Brute Force Algorithm）作为其中之一，有着计算准确性高、数值稳定性强等特点。蛮力法通过遍历所有的网格中心点，计算该点到构造模型所有三角形的距离，取最小值作为输出结果。该算法容易实现并行，为此，可通过OpenMP 并行库对其进行并行加速。下面，本文将对利用OpenMP 并行库加速模型烘焙出符号距离场算法进行详细描述。

2 并行加速模型转符号距离场

不同模型有着不同的三角面片数量，伴随着不同的复杂程度。对于复杂的模型，则需要利用更为精细的网格对其进行表示，即需要构造更高分辨率的符号距离场。在确定相应分辨率后，可计算出相应的网格中心点。在蛮力法中，根据网格中心点在模型空间的坐标位置，遍历所有三角网格，计算该点距三角网格的最近距离，作为最终的距离值。同时，根据三角形的顶点顺序确定相应符号，最终得出符号距离值。

2.1 空间中点到三角形最近距离计算

蛮力法生成符号距离场过程中的计算空间中点到三角形的最近距离是极为关键的一步，其计算正确才能保证符号距离场构建准确。

Jones 等人[6]提出一种快速有效的点到三角形最近距离的计算方法。首先，确定网格分辨率，计算出相应的网格中心点坐标p。其次，将网格中心点p投影到三角形所处的平面中，并计算出相应的投影点坐标p'。然后，通过重心法判断p'是否处于三角形中，若处于三角形中，则距离值为网格中心点和投影坐标点的矢量距离。反之，则需进行进一步计算，即计算三角形三条边中距离p'最近的点q的坐标位置，最终距离值为点p和点q之间的欧氏距离。该方法在保证距离计算的正确性，能够确保数值的稳定性，同时易于并行加速。

2.2 距离值符号确定

蛮力法确定距离值后，便需进行对该距离值符号得确定，进一步表达相应网格中心点相对于物体信息，即该点处于物体内部还是外部。符号得确定是保证符号距离场构建正确的关键之一。

符号距离值得符号可通过公式（4）进行确定。其具体思想为，在给定空间中任意一点坐标位置p 的条件下，通过2.1 小节中计算的最近点q，确定矢量(p-q)。同时，计算出q点所在三角形的法向量。计算矢量(p-q)和法向量n的夹角，若夹角大于90 度，则确定符号为-1，等于90 度，为0，小于90 度则为1。为方便计算，可通过公式（4）中点乘的正负值进行相应确定。在计算出符号后，通过符号和距离值得乘积确定符号距离值。

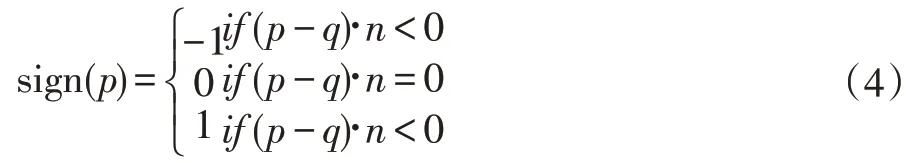
然而，由于构造模型的三角网格往往共享相同的边，通过公式（4）进行符号计算，可能存在符号计算不正确的情况。如图2 所示，通过2.1 小节找到最近的三角形，则会存在两个三角形都满足的情况。然而，两个三角形根据公式（4）所计算出的符号却截然相反。为此，可以通过平均混合两个三角形的法线得出最终用于确定符号得法线值n' 。通过n' 和(p-q)代入公式（4）中计算出最终的符号距离值。

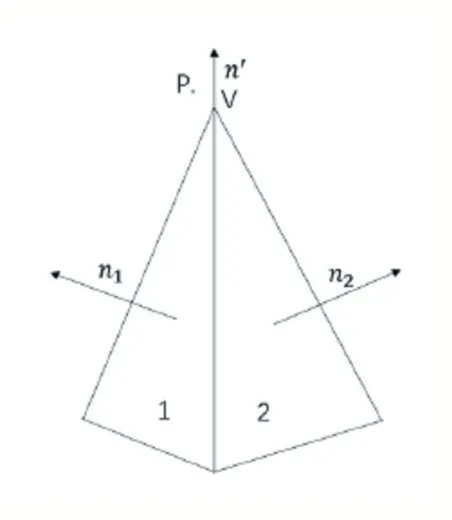
图2 点P 处于顶点V ，两个三角形1、2共享点P

2.3 OpenMP并行加速

在过去的一些年中，实现并行计算的方法多种多样。CPU 上的并行计算一般基于OpenMP 或MPI，分别适用于共享内存多处理器系统和分布式内存并行系统。MPI 适用于粗粒度并行计算，特别是集群系统；OpenMP 适合细粒度并行计算，通常用于对称多处理器平台（SMP），它充分利用了CPU 中的多个处理核心[7]。由于在符号距离场中需要遍历网格中心点及物体所有的三角面片，在C++环境中利用模型生成符号距离场的工作通常在SMP 上进行，因此基于OpenMP 的并行计算对加速符号距离场的生成更为实用。

OpenMP 由一组描述并行性的编译器指令和一个支持的子程序库组成[8]。OpenMP 基于多线程的方法，采用标准的fork-join 并行化模型，如图3 所示。串行域中的主线程（连续执行一系列指令）在遇到并行域时分叉出指定数量的从线程(Tid0,Tid1,Tid2,…)，这使得系统在这些线程之间划分一个任务，然后这些线程并行独立地运行。在并行化代码完成后，这些线程重新连接到主线程中，主线程继续连续执行指令。OpenMP可以直接嵌入到源代码中，从而为串并行转换提供了一个简单的快捷方式。基于OpenMP 的并行计算模型具有低延迟、高带宽的特点。为此，利用OpenMP 可并行加速符号距离场的生成，能够大大减少生成耗时。

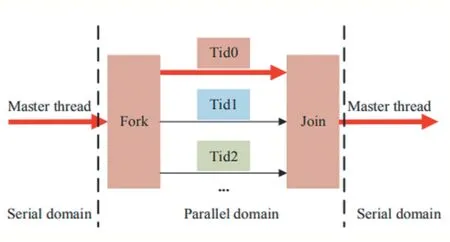
图3 Fork-join多线程处理模式

3 实验结果

本节将会对利用OpenMP 并行加速构建符号距离场进行效率测试。同时，在模型生成符号距离场后，利用球体追踪的方式可视化符号距离场，以验证符号距离场构建的准确性。实验的主要软硬件环境配置如下所示。

硬件环境：

CPU：Intel Core i3-6100 CPU@3.70GHz

内存：20.0GB

显卡：NVIDIA GeForce GTX 1060 3GB

软件环境：

操作系统：Windows 10

编译器：Visual Studio 2019

开发库：C++、STL、OpenGL

表1 为本算法计算不同分辨率的符号距离场的程序运行时间。

表1

图4 展示利用龙模型生成的符号距离场，通过球体追踪的方式进行模型绘制。

4 结语

本文给出了一种基于OpenMP 并行加速生成符号距离场的算法。通过输入构造模型的网格文件，计算出相应的符号距离场，并且对其加速效率进行测试，及利用球体追踪方式对其可视化，验证距离场构建的准确性。

图4 龙模型和其符号距离场，符号距离场分辨率为64×64×64

通过本文的方法可以快速生成符号距离场，但是符号距离场的构建时间仍然和模型的三角网格数量，以及烘焙的分辨率存在正相关的联系。在模型数量过多，分辨率过高的情况下，生成距离场所需的时间仍然很多。为此，在接下来工作中，可通过GPU 加速的方式进行进一步加速生成符号距离场。