基于特征感知的三维点云简化算法研究

苏江姗

（四川大学计算机学院，成都610065）

0 引言

随着三维激光扫描技术和硬件处理能力的提高，使用点云对三维模型进行表示和绘制在过去十几年中得到了广泛的应用，点云模型的处理技术也受到了计算机图形领域的关注。随着扫描设备的精密化，获得的点云数据精度和密度越来越高，若直接对点云数据进行管理与渲染会消耗计算机大量的处理时间，并且会占用很大的储存空间。在实际应用中，高精度的点云在许多情况下并不必要，因此多三维点云模型进行简化就十分有必要。

早期点云简化算法主要研究在简化的过程中如何更好地保留点云模型的集合特征。Alexa[1]提出基于移动最小二乘法（MLS）的简化方法。该方法的主要思想是计算每个点到MLS 拟合平面的距离，并且不断移除距离最小的顶点。Scheidegger[2]提出将基于MLS 的方法扩展至局部邻域点的拟合曲面简化。Pauly[3]基于曲面变化度分别提出顶点聚类法、迭代法和粒子模拟法，对比三种简化方法在不同衡量标准下的优劣得出结论。基于迭代的简化方法具有最小的简化误差，但在简化过程中无法控制简化后顶点的密度。顶点聚类法具有最快的简化效率，但简化前后模型产生较大的误差。基于粒子模拟的简化方法可以较好地控制模型表面顶点的分布，但简化效率不佳。Song[4]提出基于全局聚类的点云简化方法，该方法通过使得简化前后的几何误差最小化得到全局最优解。

点云模型数据除了能表示模型的位置信息，有些点云数据还含有法线颜色信息。因此在简化时考虑颜色误差、法线变化率等也成为了相关领域研究者的关注点。Miao[5]提出了一种可以识别曲率的适应性采样算法，该研究提出了一套适应性的均值漂移聚类方案来生成非均匀分布的采样结果。Huang[6]提出了保留几何和颜色特征的误差度量方法，优先考虑对误差较小的局部邻域合并达到简化目的。Leal[7]提出基于点云局部密度的简化方法，该方法对点云中的噪声点和异常点具有较好的鲁棒性。

在点云简化算法研究中，如何在最大程度地保留细节特征的前提下减少点云数据量是研究的关键。现有的点云简化方法可分为两类：一类方法是基于顶点聚类的简化，另一类则是计算点云局部复杂度并迭代删除顶点的简化。

基于顶点聚类的简化方法分为两种：一种是基于体素划分的点云聚类。对点云模型按照一定的单元大小进行空间上的均匀体素划分，并将点云中的点划分到相应体素单元中，每个体素单元保留离质心最近的顶点作为该体素的简化结果。由于体素尺寸的固定，该方法不能适用于不均匀采样的点云模型，并且在均匀采样的模型细节复杂处与模型细节简单处保留大致相同的顶点数，导致模型细节在简化后得不到更好地保留。同时，使用该方法时如果体素尺寸过大，模型表面不连接的部分容易被划分至同一体素，造成简化结果错误。另一种是基于点云模型表面的聚类，可以将整体点云模型自上而下进行划分生成基于模型表面的聚类，也可以通过区域增长法收集邻近点云区域逐渐产生基于模型表面的聚类。该方法适用于均匀与不均匀采样的点云模型，但该方法在聚类时仅考虑在局部区域寻找最优解，因此会造成部分生成的聚类跨越特征边界的问题。另一类基于迭代删除点的简化方法则是通过在一定邻域内计算点的局部曲面参数值和颜色变化度来衡量局部表面的复杂程度，根据点云模型中点的局部复杂度由小至大迭代地删除顶点达到点云简化目的。

1 算法实现

1.1 算法描述

本文对点云场景简化方法进行研究，基于迭代和聚类的点云简化思想，提出基于特征感知的点云简化方法，通过最大程度保持点云模型表面的几何与颜色特征并减少点云数据量达到简化目的。通过衡量局部半径内点云简化前后产生的几何和颜色误差作为误差度量因子，按照每个点的误差由小至大迭代地进行邻域内的顶点聚类，直到简化程度达到用户设定的简化率。最后，实现基于点的渲染方法达到可视化的目的。假设当前顶点p的误差搜索半径为r，即简化后点云半径为r，逐顶点计算的误差简化公式为：

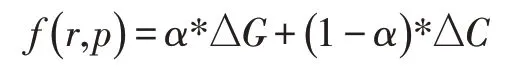
其中f(r,p)为顶点p在r半径内的误差公式，ΔG为几何误差，ΔC为颜色误差，α为误差权重值。

1.2 几何误差度量

本文使用点云模型表面的曲面变分来估计点云局部曲面的几何误差ΔG，此方法可以简单有效地反映模型表面的曲面复杂程度。曲面变分的数值越大则表明在模型局部的曲面越弯曲，若曲面变分的数值越小则表明局部点云越平坦。

假设点云模型中的任意一点记为pi，该点周围半径内点记为pk，其中pk∈NB(pi)，NB(pi)表示以pi为中心，一定半径的邻域内的K 个数据点，为pi周围邻域点的均值，即：

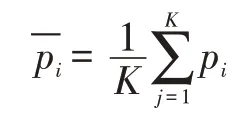
点pi的协方差矩阵定义为：

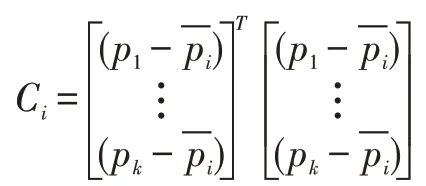
其中Ci是对称半正定矩阵，有性质：对称半定矩阵的特征值为实数，因此该矩阵存在三个实数特征值，设为x=m(u):R2→R2，它们对应特征向量分别为v1、v2和v3，v2和v3张成了点pi处的最小二乘拟合平面，v1则是该拟合平面的法向量，λ1大小表示局部邻域拟合的曲面在pi处沿法向方向的变化量。曲面变分则定义为：

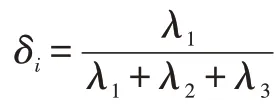
1.3 颜色误差度量

本文使用一定半径内顶点的颜色与平均颜色色差的方差作为颜色误差的度量因子ΔC，即评估一定半径内顶点颜色之间的相似程度。本节首先介绍RGB颜色空间存在的局限性，对HSV 空间色差的计算进行详细叙述。

RGB 颜色空间是使用最为广泛的颜色空间，该颜色空间利用三个通道表示颜色：红色R、绿色G 和蓝色B，通过这三个颜色分量的线性组合来表示其他任何颜色。但当需要对颜色进行连续变换时，并不能通过调整三个分量直观地反映颜色连续变化。同时，表示在自然环境下获取的颜色对亮度信息非常敏感。而通过调整RGB 分量达到亮度变化，需要对三个分量都进行调整，这种方式是不够直观的。最后，人眼对红绿蓝三种颜色分量的敏感程度也是不同的，眼睛对红色较为不敏感，却对蓝色最为敏感，因此使用RGB 颜色空间表示的颜色，通过人眼观察均匀性较差。

在精确表示颜色处理的应用中，使用的通常是HSV 颜色空间的信息。HSV 颜色空间可以更直观地表达颜色的色调、明暗、鲜艳程度。方便对不同的颜色进行统一规范的比较。

由于水文序列的随机性、灰色性以及不稳定性等特征，在对径流量进行模拟预测时产生了较大的误差。而误差修正模型则是对当前预测模型的补充，该方法即克服了单一方法的局限性，又高效地提高了预测模型的适用范围以及其预测精度。文中采用ARIMA模型来对径流量模拟产生的误差进行修正，其具体步骤如下：

HSV 颜色空间可以表示为一个圆锥模型，这个模型中的颜色参数分别是：色调H、饱和度S 和明度V，如图1 所示。

图1 HSV颜色空间模型

由图1 所示，色差的计算在HSV 空间可以转换成圆锥上点的距离。在斜边长R，底面圆半径为r，高为h的HSV 圆锥体模型中，以地面圆心为原点，H=0 为x轴正方向建立坐标轴。假设色值为（H，S，V）的点的三维坐标为（X，Y，Z）：

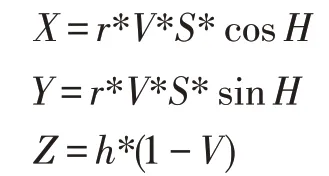
2 基于Surface Splatting的点云渲染

2.1 算法思想

为避免在使用基于点的渲染方式进行渲染时，点与点之间有镂空的问题，基于面片的渲染算法将每个点视为点面元（Surfel），通过这些面元形成几何表面进行渲染。Zwicker[8]提出了基于椭圆加权滤波（Elliptical Weighted Average，EWA）的渲染框架。该渲染框架的主要思想是在世家坐标系下利用一定邻域内的点集作为输出，重建出连续的几何表面。但是点集经过模型变换、视角变换、投影变换等操作后，在屏幕坐标系下的几何形态会出现明显的扭曲走样。因此需要直接在屏幕空间下进行二维图像的重建工作，生成光滑形态正常的结果。

2.2 算法流程

首先利用一定邻域内的点来对模型表面进行拟合。如图2 左所示，模型表面局部邻域内任意一点Q的属性是通过邻域内的点集使用定义在二维局部空间下的三维重建核拟合而成。该算法将连续曲面函数fc(u)定义为：

其中，k表示邻域点集，wk表示点的属性，例如坐标、法向量、颜色等。rk表示二维局部空间下的三维重建核，u为在局部坐标系下的曲面上任意一点。

图2 EWA基本思想[8]

接着，将连续曲面函数映射到屏幕空间，基本思想如图3 所示。该算法定义了从局部参数坐标系到屏幕坐标系的映射关系x=m(u):R2→R2，通过映射变换得到屏幕空间下连续曲面函数：

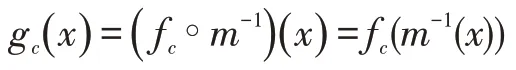
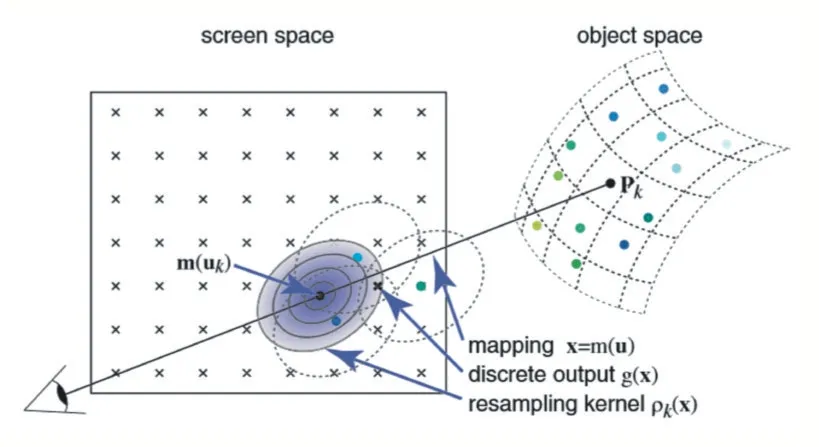
图3 局部坐标到屏幕坐标的映射[8]

其次，需要对曲面函数进行低通滤波处理。在经过模型变换、视角变换、投影变换等操作后，生成屏幕上的像素会产生走样现象，因此需要进行滤波处理。定义h(x)为低通滤波函数，与gc(x)进行卷积运算得到处理后曲面几何函数

其中，pk是屏幕空间下的重采样核。

Surface Splatting 是一种新的点云渲染方法，它将EWA 的优点用于基于点的表面的表示和渲染。该算法提供了一个完整的数学分析过程，从空间中不规则的点通过数学变换得到了基于二维屏幕坐标的函数。

3 实验结果

本节将会展示点云模型使用我们的简化算法得到的简化结果，利用基于Surface Splatting 方法进行渲染，验证简化算法的正确性。实验设备为：

CPU：Intel Core i3-4160 CPU@3.60GHz

RAM：8.0GB

System：Windows 10

GPU：NVIDIA GeForce GTX 1050

图4 展示了熊猫原始点云模型以及简化率为25%、50%和75%时相同简化半径点云的效果。

图4 不同简化率下的简化效果

图5展示了简化率为50%的屋顶模型在使用几何误差和颜色误差作为误差度量因子的简化结果，其中使用几何误差作为度量因子的简化结果较好地保留了模型的几何特征，使用颜色误差作为度量因子的简化结果更好地保留了模型的颜色特征。

图5 简化率为50%时使用几何误差和颜色误差的简化效果

4 结语

本文给出了基于特征感知的三维点云简化算法，通过输入初始点云数据和简化率目标，生成简化后的点云模型，并对简化前后的点云模型使用基于点的渲染方式进行可视化，验证了简化方法的有效性和正确性，得到的简化后模型数据可进行管理和处理。

虽然我们的方法可以得到保留几何和颜色特征的简化后的模型数据，但是当模型使用基于点的渲染方式进行可视化时，使用上述方式无法保证模型表面顶点的分布足够均匀，即简化后模型并不能保证在用点的渲染方式获得最优效果。因此，在后续的研究中会考虑模型表面点的分布情况，将模型局部顶点的紧密度作为误差度量因素，保证简化后的点云在可视化时有最优效果。