基于强化学习的机场服务机器人动态路径规划
李志龙,张建伟
(四川大学视觉合成图形图像技术国防重点学科实验室,成都610065)
0 引言
现阶段国内民航事业迈入了飞速发展的阶段,机场客流量数量也同时呈现飞速的增长。在机场旅客客流量不断增多的同时,机场行李所需的运输量也随之大幅的增长,故而机场需要雇佣更多的人工来进行机场行李的搬运装卸等工作。但是伴随着工作量的增大,行李的安全问题难以得到保障。而目前国外某机场所应用的服务机器人很好的克服了这个问题,一方面削减了人工开支,另一方面繁重的工作量并不会对行李的搬运产生影响,但是在机场中服务机器人的行驶轨迹会存在一个不确定性,且地勤人员、行李运输车等都可能会与服务机器人产生碰撞的问题,故而需要对服务机器人进行合理的路径规划。
1 问题描述
研究服务机器人实时躲避障碍问题的难点分别为复杂性、随机性、约束性和条件性等。现阶段应用较多的方法为基于随机采样的路径规划算法。例如YTing等人[1]提出了一种改进的基于RRT 的平滑RRT 方法,此算法通过设立一个最大的曲率约束来防止遇到占该物体时可以获得平滑的曲线,通过论文中的仿真实验显示,此算法比传统的基于RRT 方法拥有更快的收敛速度。AlvesNetoA 等人[2]讨论了基于PRM 方法的概率基础,结论为其中部份的先验知识能够加快算法自身的收敛速度。但是此类中基于概率的路径规划方常常很难确保每次运行期间都可以实现对期望轨迹的高精度跟踪。由一种典型的避障算法称作人工势场法,障碍物在此类算法中被冠以为某类排斥性的表面的称号,并且目标防卫则被刻画成为一种具有吸引能力的端子,这样使得机器人可以趋近最终目标任务,从而避免与障碍物发生碰撞[3]。陈钢等人[4]采用人工势场法对障碍物进行碰撞检测获取到了虚拟的排斥力,且引入臂平面和避障面设立了机械臂的动力学避障算法。申浩宇等人[5]定义了两个转换算子,且定义了一类基于主从任务转换的动力学避障算法,使得冗余机器人可以实现轻松在多主从任务之间进行平稳切换。方承等人[6]设计了基于多个目标函数的避障规划算法,主要是为了解决单独使用最短距离某些场景下会导致避障失败的问题,该算法主要为当障碍物位于机器人手臂构型内部时,以两者之间的最短距离作为避障优化指标,而当障碍物位于构型外部时,以避障区域作为替代。Lacevic等人[7]提出了一种新的安全评价方法——危险场法。该算法结合了机器人手臂与障碍物之间的位置关系、机器人手臂的使用速度以及障碍物与障碍物手臂之间产生的夹角,导致了危险场中的不稳定因素,并将其应用于修改后的CLIK 算法[8],顺利解决了例如某些顺利可变障碍物体的问题。其他方法还有如Hart、Nilsson和Raphael 提出的A*算法[9],但是这些方法都存在一个明显的问题,只是一味追求局部最优解而忽略全局解。
针对以上所分析的情况,本文采用深度学习中的Q-Learning 算法对服务机器人的路径选择学习行为进行建模,使得机器人可以在快速选择合理的路径,完善自身冲突探测和解脱知识库的不足,进一步提升自身的智能程度。
2 算法描述
2.1 强化学习相关理论
强化学习自身作为一种无监督学习方法,机器人Agent 可以借助与动态环境的反复交互,学会选择最优或近最优的行为以实现其长期目标[10]。Sutton 和Barton 定义了强化学习方法的四个关键要素:策略、奖赏函数、价值函数、环境模型[11]。如1 图表示为强化学习的主要基本模型。
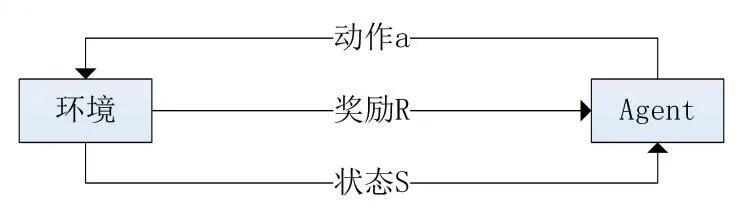
图1 强化学习基本模型
在图1 中,Agent 会依照目前环境的状态进行下一步的动作与环境产生交互,而因此会从环境中得到此不行动所产生的奖励,并更新为新的状态,进行更新策略的学习,接着再次执行下一步动作作用于环境中,反复重复此过程,直到优化策略完成任务。
2.2 Q-Learning
Q-Learning 作为一种典型的与模型无关的算法。该算法由Watkins[13]在1989 年提出,算法通过每一步进行的价值来进行下一步的动作。Q-Learning 算法首先会建立一张Q 值表,机器人自身每前进一步都和环境会产生交互,并根据每次交互的结果,机器人会得到一定的奖赏,如上述强化学习的基本过程,其中Q 表如表1 所示。
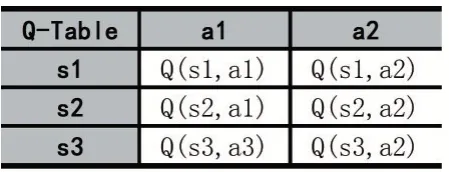
表1 Q 值表
其中算法整体的基本流程如图2 所示。
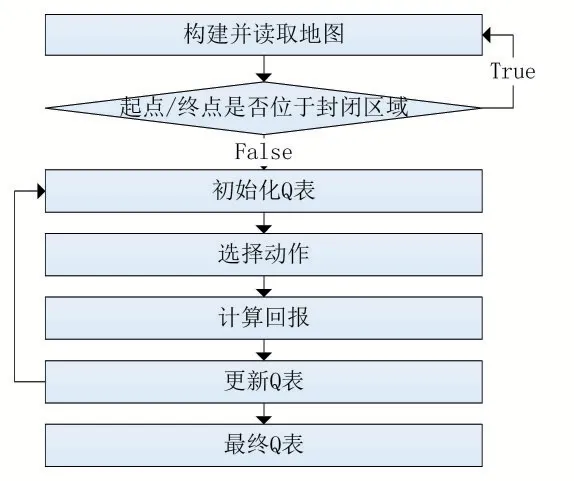
图2 算法基本流程图
Q-Learning 采用状态-动作对Q(s,a)迭代方式来获取到最优的路径策略。Q-Learning 在每次迭代的时候都会考虑每一个状态-动作组合对Q(s,a)产生的结果值。其中算法的基本形式主要为:

其中:st,为t 时刻目标机器人的移动状态,在该st,状态下执行动作at,目标机器人当前状态转化为st,+1,同时获取到此状态的奖励rt;rt主要的作用是对下一状态st,+1进行的评估,代表目标物体从前一个状态进行到下一个状态所能够得到的奖励值。动作a∈A,A 含义是作为动作空间;状态st,,st,+1∈S,S 为状态空间;α为学习率,Q 值会随着学习率的增大而收敛速度加快,但是也存在更加容易产生振荡的缺陷;maxaQ(st+1,a)代表从A 中选取某一个动作促使Q(st+1,a) 的当前获取值变为最大;γ代表了折扣因子,表示未来奖励对当前动作的影响程度[12]。
其中可以将式(1)变形为:
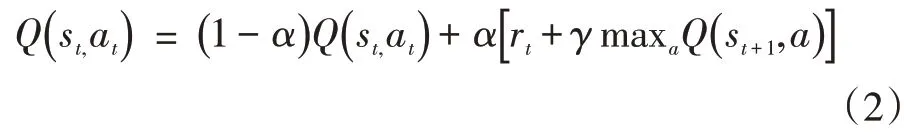
通过式(2)可得到,st所对应的Q 值稳定的必要条件需为st,+1对应的maxaQ(st+1,a) 为固定值,若maxaQ(st+1,a)为非固定值则前一状态Q 值将会随下一状态Q 值更新而发生变化,导致前序动作的状态变得不稳定。
通过对式(2)进行n 此不断迭代可以得到:

因为0 <α<1,所以当n→∞时,Q(st,at)收敛。
Q-Learning 会借助式(2)进行更新,使得完整的Q表趋向一个极限的ΔQ(st,at)=rt+γmaxaQ( )st+1,a,随着状态得不断更迭,Q 值会进行更新操作,当n→∞时,最终结果将趋向于最优值。
避免产生局部最优:Q-Learning 本质上是贪心算法。如果每次都取预期奖励最高的行为去做,那么在训练过程中可能无法探索其他可能的行为,甚至会进入“局部最优”,无法完成游戏。所以,设置系数,使得智能体有一定的概率采取最优行为,也有一定概率随即采取所有可采取的行动。将走过的路径纳入记忆库,避免小范围内的循环。
3 实验仿真
本研究使用MATLAB 软件进行仿真验证,设计基于Q-Learning 的最短路径规划算法,并考虑障碍物体的实时且随机的变化情况,更加符合实际情况。同时使用网络对Q 值更新进行一定的优化,使得Q 值表能够更加符合实际应用。
3.1 环境建模
本文在仿真实验中主要使用地图建模的方式建立一个有33 个节点的无向图,其中每两个个节点间的路径都含有一个权值,代表两点之间位移的代价,从开始点至结束点代价最小的路径则为最优路径。同时,两个节点间相连则表示两点可以互相连接,若两节点之间无路径连接或有障碍物则表明该路径不可前进,其中障碍物在本次实验中设定为随机生成,在图中第一次生成的障碍路径以红色叉号显示,之后在原本寻路路径基础上增添的新的障碍路径则设定为黑色叉号显示。

图3 原始地图
3.2 实验仿真
为了验证所设计的机场服务机器人自动避障算法可行性,采用MATLAB 软件对本算法进行仿真实验。现在我们拿其中一次实验结果举例,在本次仿真实验中,随机生成障碍路径,机器人初始时刻位于1 号节点,终点坐标位于28 号节点,障碍路径分别为9、11、19、29、34、35、41。其中总结点数量为33,单位路径数量为44,迭代次数为50,学习率α=0.9 ,折扣因子γ=0.8,试验结果如图4 所示。

图4 第一次出现障碍图
其中在实验中增加了障碍物动态变化的可能性,新增障碍路径为7、14、16、26。在变化的仿真环境中机器人路径也同时产生了优化,每次和环境产生交互都会更新其奖励值,再根据奖励值更新Q 表,最终通过环境-动作交互求得最终的Q 表,显示出其实时动态性。如图5 所示,其中黑色叉号为新增障碍路径。
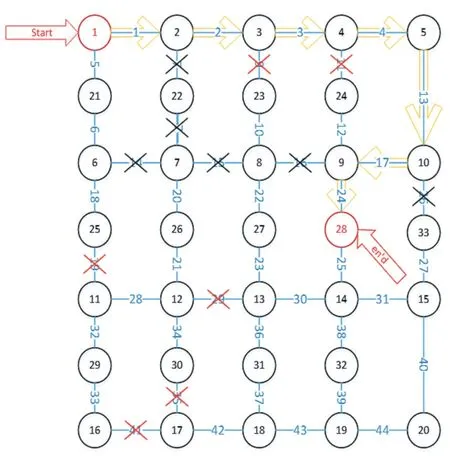
图5 第二次出现障碍图
其中由于Q-Learning 特性需要重复学习并记录相关知识库,故而在多次实验后建立了寻找最优路径时间和运行次数统计图。图6 列出了Q-Learning 和传统算法的时间和运行次数比较图,图6(a)表示传统A*算法,图6(b)为深度学习Q-Learning 算法。可以从两张图中看到随着Q-Learning 实验运行次数的增加,使用传统A*算法随着运行次数的增加,运行时间并不会减少,而在使用Q-Learning 算法中随着实验次数的增加,路径的动态变化,服务机器人顺利找到起始点到终点的最优路径所需的时间消耗呈现大幅的下降,体现了Q-Learning 算法在动态路径识别中所代表出的优势。
4 结语
(1)本文针对机场服务机器人的移动路径中可能会发生的碰撞问题及碰撞物体的动态移动问题提出了以深度学习Q-Learning 算法为基础的解决方法。
(2)此方法经过实验论证相较于传统算法也是有了较大的提升。通过对路径进行数学建模的方式进行拓扑建模化,在拓扑化之后,将所有的障碍物所遮挡的路径加入相应的知识库,该方法减少了多次运行试验后机器人寻路的时间消耗量,提高了服务机器人的运算速度,并且在运行过程中实时对障碍物所处路径进行实时更新,以模拟现场环境中人员及其他障碍物体的不确定性。
(3)在经过多次Q-Learning 实验之后,服务机器人以较短时间顺利避开行李车或机场地勤人员等障碍物,满足设计的要求。

图6

