等积变形法VS割补法

黄旭军

今天的数学课上，阿木老师在黑板上画了一组平行线，然后在里面画了两个平行四边形。然后笑眯眯地问：“大家看看，甲乙两个阴影部分的面积相等吗？”

心急的同学马上说：“甲大，一看就是甲大！”有些同学举手表示不同意见。

阿木老师点点头，接着说：“这道题就是等积变形的好例子。利用等积变形，可以让一些图形题变得很简单。

例1

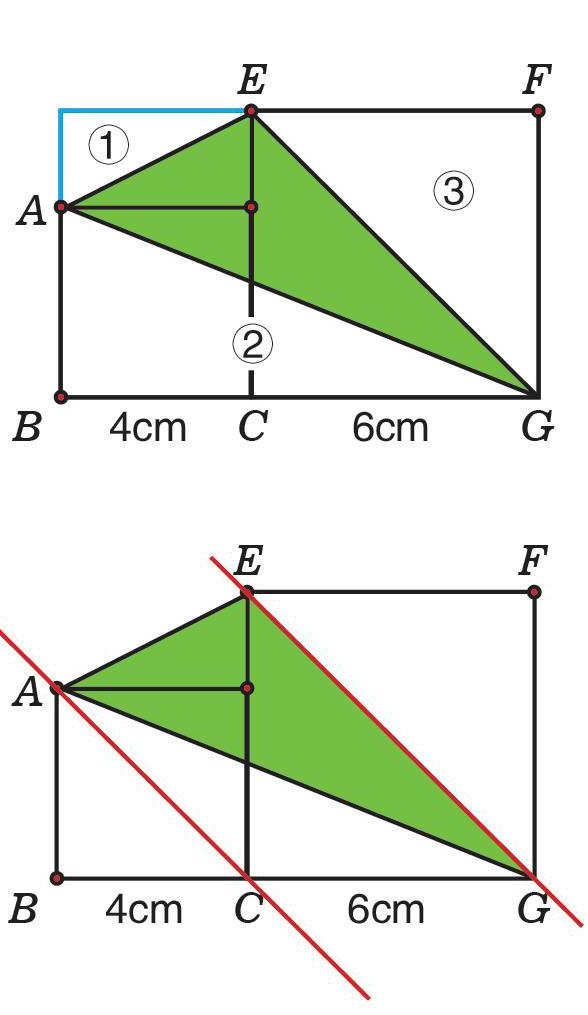
已知图中大正方形的边长是6厘米，小正方形的边长是4厘米，求阴影部分的面积。

观察

开始

所求阴影部分是三角形，但这个三角形三条边的长度都不知道，也没有高的长度，不能直接求。

常规

思路

如果用割补法解决的话，如右图，先补出一个大长方形。

然后再从大长方形的面积里减去白色部分的面积。

长方形面积=（4+6）×6=60（平方厘米）

三角形①面积=（6-4）×4÷2=4（平方厘米）

三角形②面积=（6+4）×4÷2=20（平方厘米）

三角形③面积=6×6÷2=18（平方厘米）

所求阴影部分面积=60-4-20-18=18（平方厘米）

答：阴影部分面积是18平方厘米。

另辟

蹊径

用等积变形法来解决。

如图，先画出两条对角线，正方形对角线与水平面都成45度角，所以这两条对角线是一组平行线。

平行线之间进行等积变形。

如图，这些三角形的面积都与原三角形相等。

其中三角形ECG不但面积与原三角形相等，计算时也非常方便。算出它的面积就等于阴影部分面积。

三角形ECG面积=6×6÷2=18（平方厘米）

答：阴影部分面积是18平方厘米。

例2

边长分别为1厘米、2厘米、3厘米的三个正方形摆成如下形状，求阴影部分的面积。

观察

开始

阴影部分是一个三角形，可是没有任何边长和高的信息。

常规

思路

用割补法来解决问题。

如图1，把阴影部分切成两个三角形。

把它们看成底都是2厘米的三角形。

左边红三角形面积=2×（1+2）÷2=3（平方厘米）

右边蓝三角形面积=2×3÷2=3（平方厘米）

所以阴影部分面积=3+3=6（平方厘米）

答：阴影部分面积是6平方厘米。

另辟

蹊径

用等积变形来解决。

如图2，正方形的两条边是一组平行线，把左边红三角形等积变形。

同理，把右边蓝三角形也等積变形，如图3所示。

经过二次等积变形，所求阴影部分面积就是图4三角形面积。

阴影部分面积=（1+2+3）×2÷2=6（平方厘米）

答：阴影部分面积是6平方厘米。

训练一二一

如图，在一个长18厘米，宽5厘米的长方形中，空白部分面积是多少？

上期答案：设圆的半径为r，则阴影部分面积为r2÷2=6（平方厘米），所以r2=6×2=12，圆的面积为3.14×12=37.68（平方厘米）。