基于粒子群优化算法的多能互补系统经济调度研究

赵鑫，郑文禹，侯智华，陈衡，徐钢

（华北电力大学能源动力与机械工程学院，北京102206）

0 引言

一直以来，煤、石油、天然气、太阳能、风能的利用大多局限于单独规划和运行，无法充分发挥多种能源的互补与协同优势。在能源危机与环境污染的双重压力下，多能互补系统的建设在我国乃至全世界引起了广泛关注［1-2］。如何提高可再生能源的消纳比例，实现能源的梯级利用，保证电力系统安全、低碳、稳定、高效、经济运行，是目前亟须解决的问题［3-4］。针对该问题，考虑将分布式能源与传统能源系统相结合，形成多能源系统，协同运行多种形式的能源，发挥不同能源的优势和潜能，实现资源的优化配置和可再生能源利用的最大化。为此，研究人员提出了微电网、综合能源系统、智能能源系统等概念［5-8］，从不同角度对多源系统的整体架构进行了阐述说明。

多能互补系统的能源形式包括天然气、柴油、生物质能、太阳能、风能、氢能、水能等；在供能端对不同类型的能源进行有机整合，提高能源利用效率，减少弃风、弃光、弃水现象；在用能端将电、热、冷、气等不同能源系统进行优化耦合，同时综合考虑经济性以及用户的舒适性，提供安全可靠的能源，促进能源利用最大化［9］。

多能互补系统可以发挥不同能源的优势，丰富可再生能源的消纳路径，提高可再生能源的利用比例，提高能源的利用效率，从而达到经济、环保、效率的最优。2016 年国家发改委、能源局印发了《推进多能互补集成优化示范工程建设的实施意见》，指出建成终端一体化集成供能系统，因地制宜实施传统能源与风能、太阳能等能源系统的开发利用，通过天然气热电冷联供等方式实现多能互补和协同供应，提高能源的综合利用效率；同时提出了“十三五”期间的建设目标，明确了开展多能互补集成优化项目的评审标准和优惠政策，规范了项目实际核实与督查机制。

多能互补是按照不同资源条件和用能对象，采取多种能源互相补充，以缓解能源供需矛盾，合理保护和利用自然资源，同时获得较好的环境效益的用能方式。多能互补的特点：（1）包含了多种能源形式，构成了丰富的供能结构体系；（2）多种能源之间相互补充和梯级利用，达到一加一大于二的效果，从而提升能源系统的综合利用效率，缓解能源供需矛盾。

目前，制约多能互补分布式能源系统发展的主要问题在于技术水平和投资回报2个方面。由于各类可再生能源尚未实现平价上网，加之关键储能技术成本不具市场竞争力，经济成本成为多能互补系统的主要短板，阻碍其大规模推广应用。随着我国一批多能互补示范项目的开工建设，诸多问题逐渐显现出来，其中亟须解决的是多能互补发展理念不明确、系统集成方法不清晰等问题。

文献［10］梳理了系统优化的内容和路径，探讨了优化路径中现有的研究方法及其不足，总结了多能互补分布式能源系统发展所面临的关键问题。为了提高能源利用率，实现节能减排，文献［11］设计了一种集成太阳能利用和内燃机驱动传统联供系统的太阳能冷热电三联供系统，对其能量流程和运行策略进行了分析。文献［12］建立了冷热电联供型微电网数学模型，综合考虑了各微电源的运行维护费用、燃料费用以及购售电费用等，采用改进粒子群优化算法，以运行成本最小为目标进行计算仿真。

以上相关研究中，关于多能互补系统优化模型中约束条件的考虑相对欠缺，与实际情况有一定差距。本研究对多能互补系统中各设备单元独立建模，综合考虑运行中设备间的制约关系，采用粒子群优化算法，以运行成本最小为目标进行仿真。最后以某小区为例，对结果进行分析讨论。

1 系统建模

传统能源系统主要对电、热、冷、气等单一能源形式进行分析规划，或者针对单个设备进行建模仿真和优化运行，而不考虑各能源间的协同优化［13-14］。多能互补系统的一个重要特征是供能端和用能端存在多种不同能流系统的耦合，各系统模型不同，特性差异大且具有不同的建模和分析方法［15-16］。多能互补系统的优化策略主要是以系统成本为目标函数，以可靠性指标或环境影响指标为约束条件建立数学模型，利用多种算法分析多能互补系统最优化问题［17-24］。为了更清晰地描述系统结构，本研究采用电冷热母线式结构进行系统建模。具体而言，根据电负荷、热负荷、冷负荷3类能量产品建立功率平衡的约束，从而实现各设备之间的连接。从需求侧来讲，冷负荷是为保持建筑物的热湿环境和所要求的室内温度，由空调系统从房间带走的热量或在某一时刻需向房间供应的冷量。相反，如果空调系统需要向室内供热，为补偿房间损失热量而向房间供应的热量称为热负荷。利用图1所描述的系统组成和结构关系，可以方便地列出能量平衡约束。

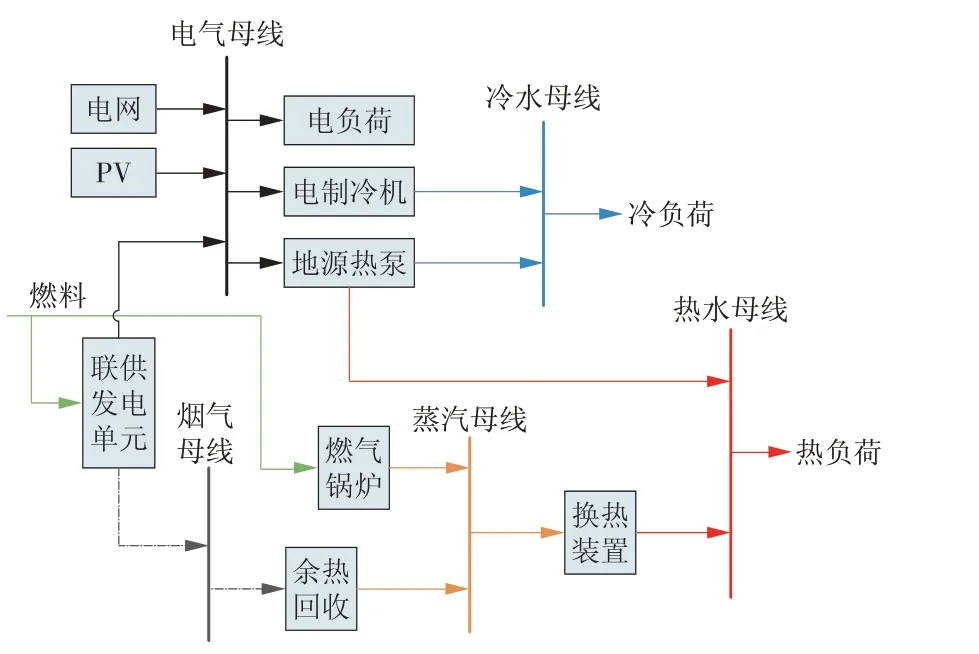
图1 多能互补系统能量流动Fig.1 Energy flow in the multi-energy complementary system

2 动态经济调度的数学模型

根据图1 中的5 种母线（电气母线、烟气母线、空气母线、蒸汽母线、热水母线）可以列出如下公式，公式的左侧为能源的输入，右侧为能源的输出。

（1）在电气母线平衡式子中，多能互补系统用户侧的电负荷由电网、燃气轮机、光伏、风机、储能设备等提供。

（2）热水母线平衡。多能互补系统用户侧的热负荷由燃气轮机回收的余热、燃气锅炉的热功率和地源热泵等提供，燃气轮机余热由换热装置转化为生活热水提供给用户。

制热模式为

2.1 目标函数和约束条件

2.1.1 目标函数对于并网运行的多能互补系统，日动态经济调度模型的目标函数为

2.1.2 约束条件

除了系统的能量平衡，还需要考虑各设备自身的约束，如各设备功率的上下限约束

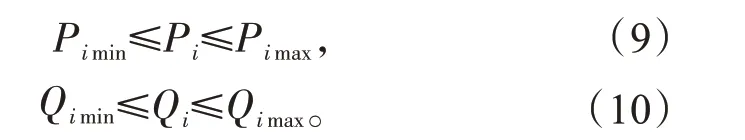
2.2 求解方法

优化算法是多能互补分布式能源系统优化过程中重要的求解工具，目前用于该领域优化的算法很多。优化算法可分为传统经典算法和现代智能算法，本文采用现代智能算法中的粒子群优化算法（Particle Swarm Optimization，PSO）寻求最优解。

粒子群算法是在1995 年由Eberhart 博士和Kennedy 博士提出的，它源于对鸟群捕食行为的研究。其核心是利用群体中个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化，从而获得问题的最优解。设想这么一个场景：一群鸟在觅食，所有的鸟都不知道食物在哪里，但是它们知道自己当前的位置距离食物有多远，那么找到食物的最佳策略，也是最简单有效的策略就是搜寻目前距离食物最近的鸟群周围的区域。

在PSO 中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”，而问题的最优解就对应于鸟群寻找的“食物”。所有的粒子都具有一个位置向量（粒子在解空间的位置）和速度向量（决定下次飞行的方向和速度），并可以根据目标函数来计算当前所在位置的适应值，可以将其理解为距离“食物”的距离。在每次的迭代中，种群中的粒子除了根据自身的经验（历史位置）进行学习，还可以根据种群中最优粒子的经验来学习，从而确定下一次迭代时需要如何调整飞行的方向和速度。就这样逐步迭代，最终整个种群的粒子趋于最优解。

假设维度为m 的n 个粒子计算适应度函数，获得使之达到最值的每个粒子的历史最优位置p和群体中所有粒子的历史最优位置g，并根据式（11）与（12）迭代更新各粒子的速度v和位置x

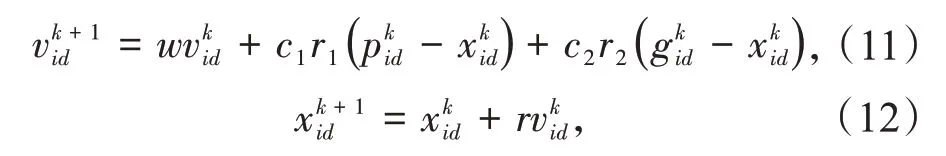
式中：i 表示第i 个粒子；d 表示第d 维空间；k 为迭代次数，可设置阈值使迭代停止；w 为惯性权重因子，表示粒子维持上一次迭代速度的能力；c1，c2为加速因子，分别表示粒子迭代倾向个体最优位置和群体最优位置的权重；r 为收敛因子，表示对位置移动幅度的控制，r1和r2为［0，1］区间内均匀分布的随机数。

3 案例分析

3.1 案例介绍

本文选取湖北省某医院为研究案例，该案例中各设备功率上限见表1，主要设备参数见表2。该区域分时电价与天然气价格见表3，其中，天然气价格2.270 元/m3折成热值后的价格为0.254 元/（kW·h）。分别选取夏季和冬季2 个季节的典型日进行优化，夏季、冬季的日负荷与光伏出力预测曲线分别如图2、图3所示。

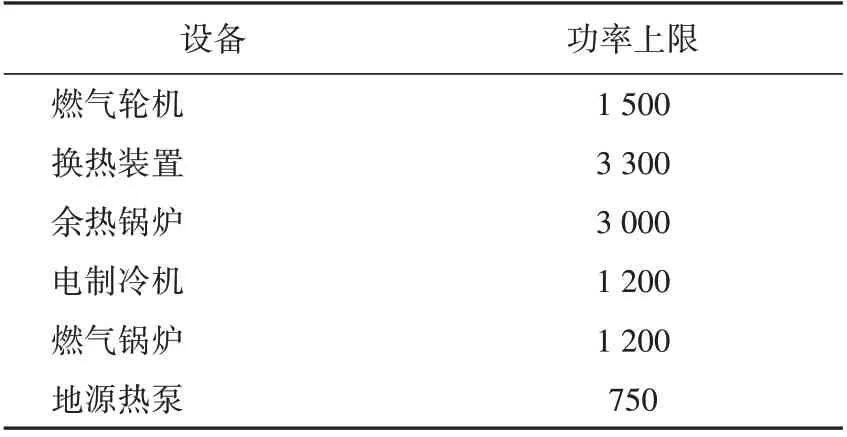
表1 主要设备功率上限Tab.1 Output power upper limit of main devices kW

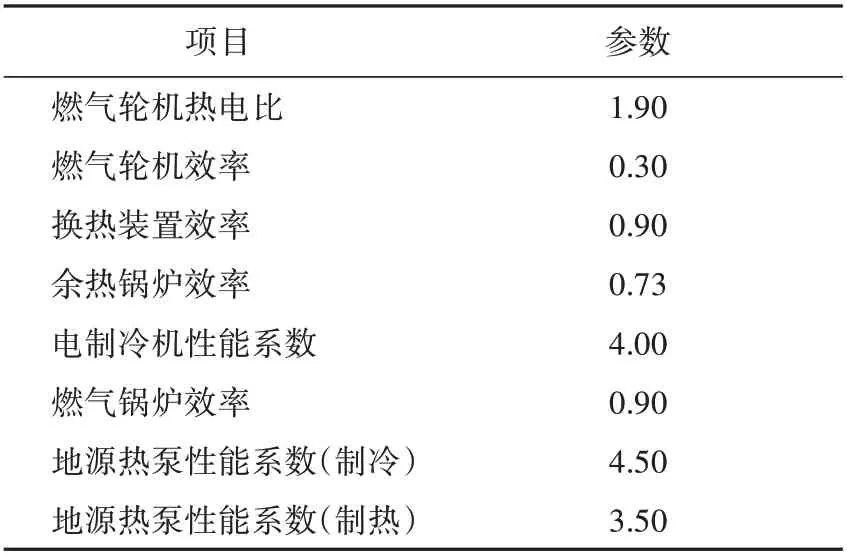
表2 主要设备参数Tab.2 Parameters of the main device

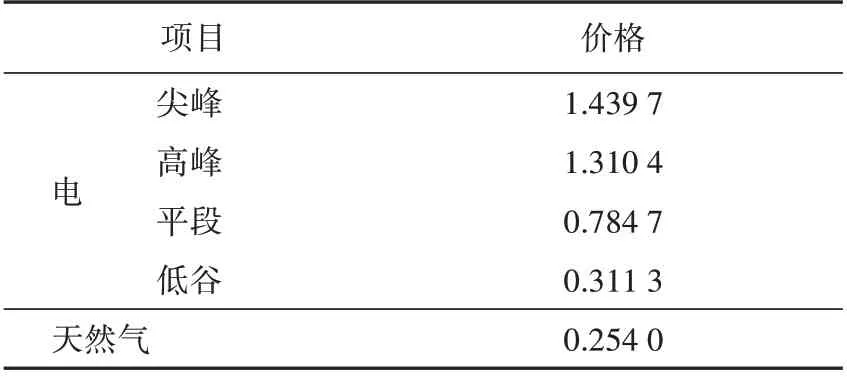
表3 分时电价与天然气价格Tab.3 Time-of-use price and natural gas price 元/（kW·h）

由图3 可见，冬季最大热负荷出现在08：00 前后，原因是冬季早晨气温较低以及医院各部门开始工作。随着白天光照变强，环境温度升高，热负荷逐渐减小。

3.2 优化结果分析

从图4 可以看出，系统优先使用光伏等可再生能源，但由于该项目可再生能源有限，电能主要来源于电网购电。从图5可知，夏季热能需求较少，由于地源热泵夏季用于制冷，热能全部由换热装置提供。

图2 夏季日负荷和光伏出力预测曲线Fig.2 Predicted curves of daily load and PV output in summer

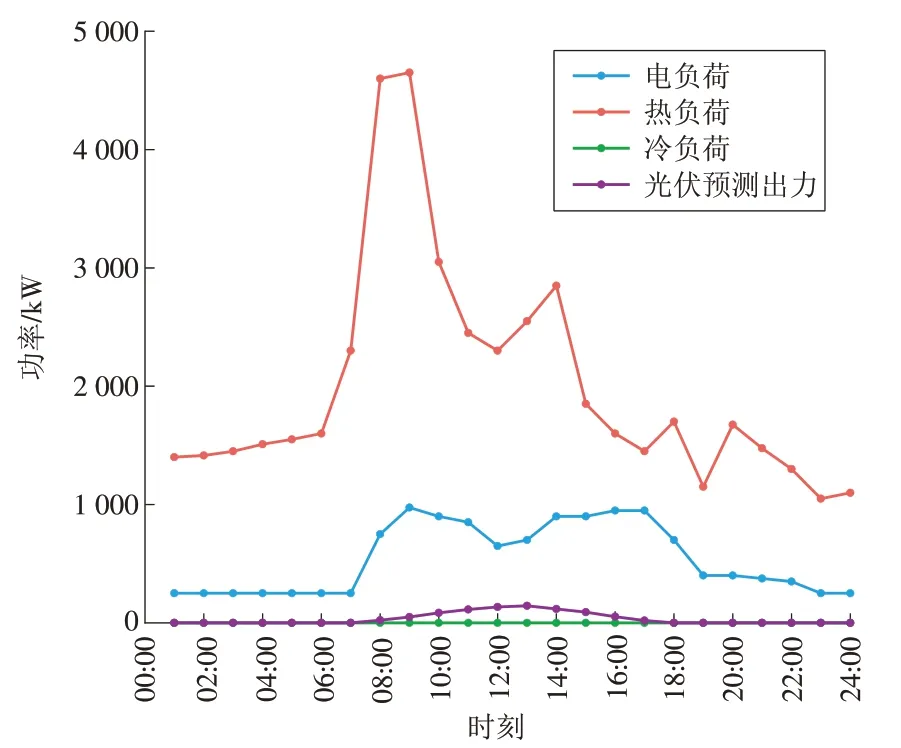
图3 冬季日负荷和光伏出力预测曲线Fig.3 Predicted curves of daily load and PV output in winter

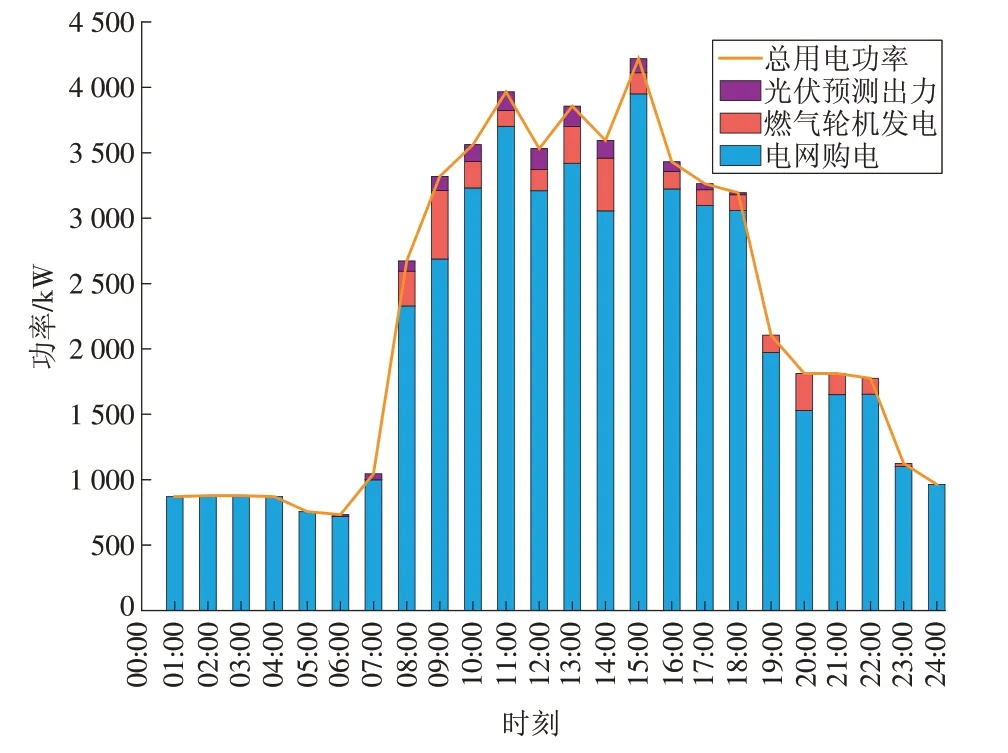
图4 夏季电功率优化调度结果Fig.4 Optimized dispatch results of electric power in summer

从图6 可知，地源热泵为主要供冷设备且全天24 h 运行，电制冷机仅在白天地源热泵供应不足时启动工作。

图5 夏季热功率优化调度结果Fig.5 Optimized dispatch results of heat power in summer

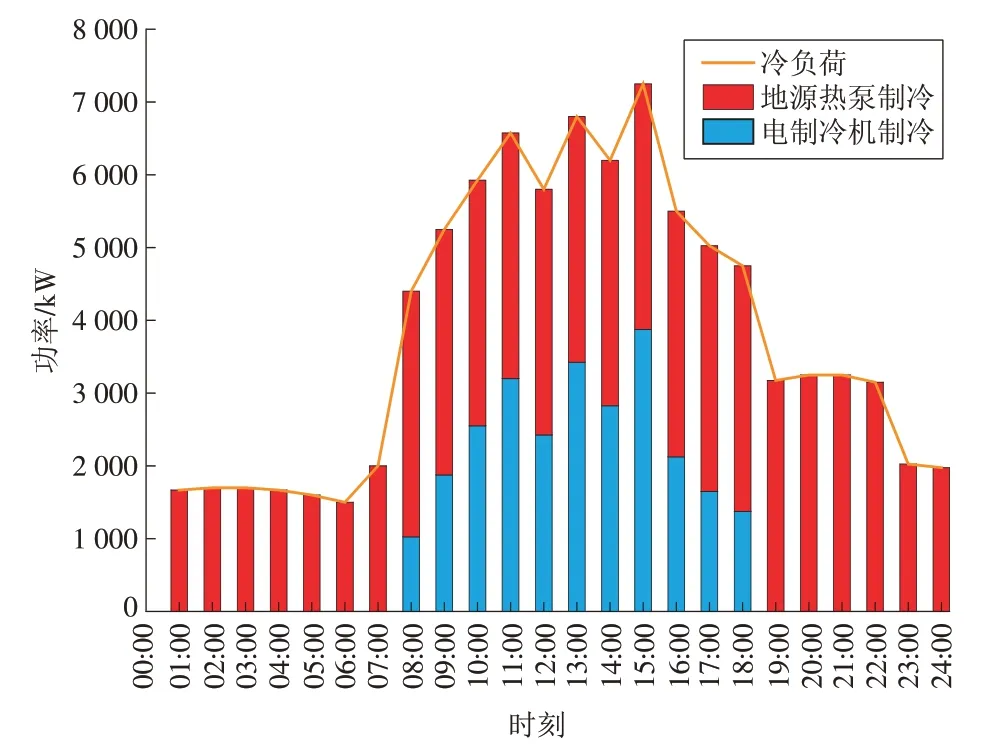
图6 夏季冷功率优化调度结果Fig.6 Optimized dispatch results of cold power in summer

由图7 可知，冬季典型日夜间电能来源于电网购电，白天由燃气轮机发电和光伏发电提供，有太阳能时优先利用太阳能。其原因为：冬季夜间热能需求较少（如图8所示），采用地源热泵即可满足，故燃气轮机不工作，电能由电网提供；白天热能需求较大，地源热泵无法提供全部所需热量，故需要燃气轮机产生的余热来供热，自然要利用燃气轮机所发的电量，所以白天优先选择光伏供电，其次选择燃气轮机发电，不足的电能由电网提供。

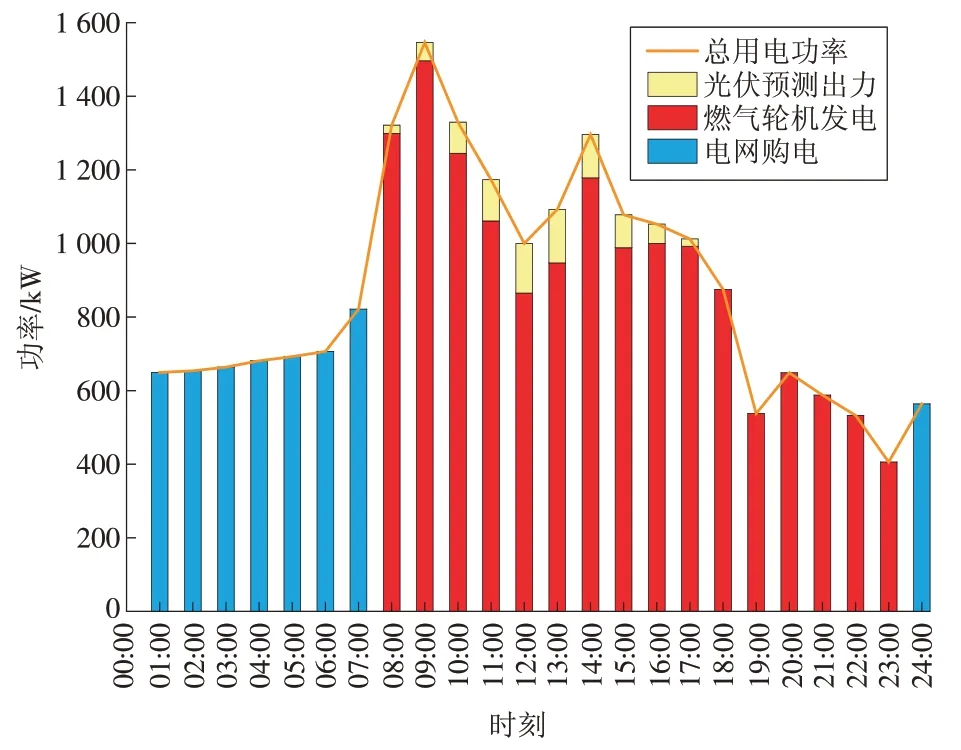
图7 冬季电功率优化调度结果Fig.7 Optimized dispatch results of electric power in winter

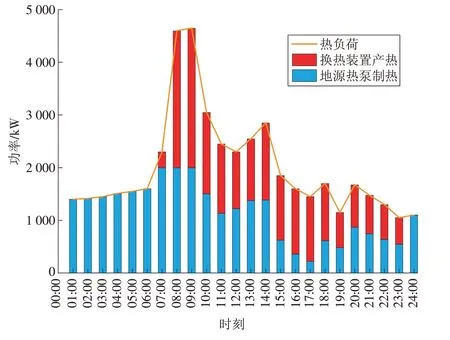
图8 冬季热功率优化调度结果Fig.8 Optimized dispatch results of heat power in winter

从图8 可以看出：地源热泵为冬季主要供热设备且全天24 h 运行；来自换热装置的热能仅在白天供热，原因是换热装置的能量是前端燃气机组发电的附属品，若不加以利用则会浪费，故此时优先供热，不足的热能再由地源热泵提供。

案例优化调度结果如图4—8所示，系统夏季日总运行成本为53 309 元，冬季日总运行成本为14 747元。优化后的系统方案具有以下特点。

（1）系统可以通过分时电价的波动进行削峰填谷；燃气轮机运行受电负荷以及热负荷影响，在平时段与峰时段运行；光伏等可再生能源在日间运行，优先利用，可以减少系统的购电量，降低运行成本。

（2）夏季热能由换热装置提供，冷能由电制冷机和地源热泵共同提供且受电价影响；燃气轮机在平时段和峰时段开启，同时提供电能和热能。冬季热能主要由地源热泵提供，换热装置作为补充，由于地源热泵效率较高，冬季运行成本较低。

4 结束语

本文在冷热电联供系统通用框架的基础上构建了动态经济调度模型，模型充分参考了不同设备间的耦合关系，并且通过各设备独立建模提高了系统配置的灵活性和准确性。结合该结构的特点，采用智能算法寻求最优解。结果显示，通过求解该模型得到满足系统负荷需求的合理方案，证实了本文模型和方法的正确性和有效性。

随着绿色低碳环保经济的发展和智能电网的建设，接近用户侧、环境友好型的多能互补式分布式能源系统将受到更多青睐。该模型可扩展应用于区域性的多能源系统，如具有光伏板的学校、住宅园区及农村等。在拥有大量光伏板的学校，可利用蓄电装置存储多余电量，在本文模型中加入蓄电池模型，同样能节约成本。对于园区类，可以加上蓄电以及储热装置，从而减少能量浪费。农村可建立大型沼气池，提供可再生能源，代替天然气的使用，满足村庄的用能需求，同样能利用本文模型，通过改变能源输入模式来达到运行优化的目的。