一种基于NoC多核系统的矩阵乘法映射技术

汪 杨，王晓蕾，袁子昂，袁儒明

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)

矩阵乘法在数字信号处理、工程控制、神经网络以及图像处理等领域中有着重要的应用[1-2]。随着待计算矩阵规模的不断扩大，实现一个大规模且有较高运算性能的矩阵乘法器具有重大的工程意义。

脉动阵列算法[3]是将复杂的计算形成硬件结构的一般方法，其巧妙地将矩阵乘法自身良好的运算并行性和硬件的并行特性结合在一起，为后续研究利用硬件结构实现复杂的运算奠定了基础。在FPGA上实现脉动阵列矩阵乘法已经取得了一些研究成果。在浮点矩阵乘法方面，文献[4]在基于FPGA上实现了实时双精度浮点矩阵乘法，在稠密矩阵乘法运算中获得了较高的计算性能，并对稀疏矩阵进行了优化处理。但针对大维度的矩阵乘法，上述方法的I/O带宽成为制约性能的瓶颈。文献[5]提出了一个基于FPGA的Systolic乘法，保留了脉动阵列的运算速度。但随着矩阵规模的增大，该算法需要的运算资源和I/O带宽成比例增长，限制了该设计的可扩展性，导致实用性较低。

上述研究虽然在特定规模下的矩阵乘法中获得了优越的加速性能，但随着矩阵规模的变化，上述方案的性能优势难以体现，对不同维度的矩阵乘法通用性不高。另一方面，脉动阵列需要一个全局时钟来控制全部的运算节点，必然会存在大量的时钟偏移(Clock-Skew)问题[6-8]。随着集成电路制造工艺的迅速发展，特征尺寸越来越小，工作频率不断提高，时钟偏移和连线延时对设计工作具有重大影响，甚至会导致整个设计系统出现问题。

NoC(Network on Chip)作为一种全新的片上系统设计方法[9-14]，不仅克服了单一时钟频率同步全局芯片工作方式带来的种种制约问题，还可以通网络灵活地构建多种运算结构，克服了固定运算结构中提高特定规模矩阵乘法性能的局限性，具有较好的适应性和扩展性。本文研究在有限的I/O带宽资源约束下，对不同维度的矩阵乘法运算进行任务调度及资源分配，充分利用了NoC通信并行性和多核系统计算并行性，提高了矩阵乘法的计算效率。

1 矩阵乘法分析

常采用的并行矩阵乘算法有旋转矩阵元素(Cannon)算法、复制矩阵元素(DNS)算法，以及采用流水线(脉动阵列)算法。Cannon算法源于空间对准思想，需要预先在运算节点中分配好数据，此过程处理难度较大，不易于实现。DNS算法是面向立方体的处理器结构，其结构难以表示。脉动阵列算法结构简单且分布规则，数据按照流水线的形式直接输入到节点中，更易于设计实现[15]。

给定两个矩阵A和B，矩阵C=A·B表示二者的积，如式(1)和式(2)所示。

(1)

(2)

这些方程的空间表示如图1所示。

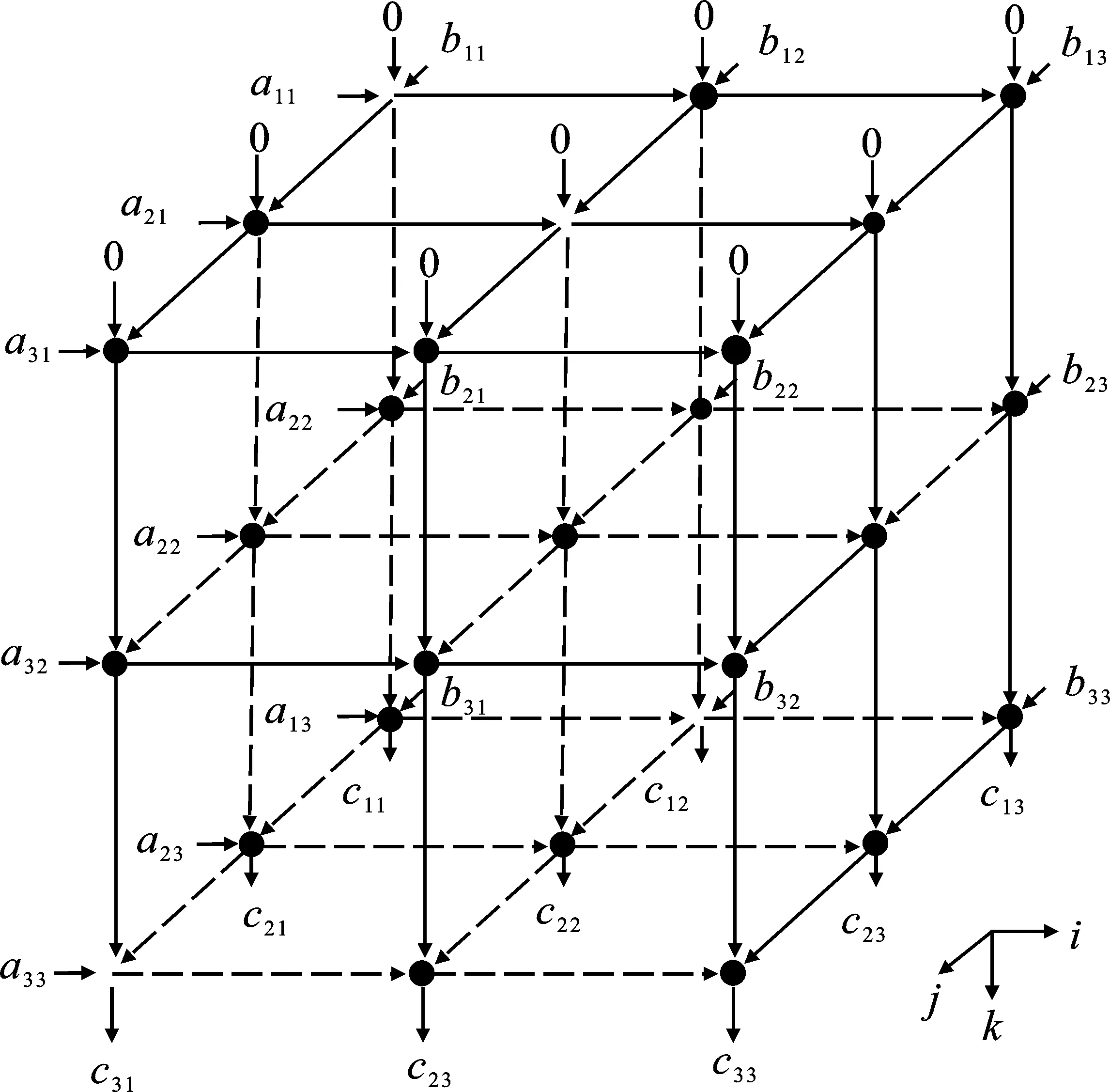
图1 矩阵乘法的三维空间图

脉动算法源于时间对准思想。首先，对矩阵的行列向量进行分配，将数据输入到运算节点中，计算的结果进行本地缓存，并作为下一次计算的中间值，用于计算的数据传入相邻的运算节点中执行运算，直至该向量运算结束。由图1可以看出，矩阵A的行向量(a11,a12,a13)、(a21,a22,a23)、(a31,a32,a33)分别进入i轴方向的运算节点，矩阵B的列向量(b11,b12,b13)、(b21,b22,b23)、(b31,b32,b33)分别进入j轴方向的运算节点，通过k轴方向上的节点运算后得到结果矩阵C，简化的依赖图如图2所示。

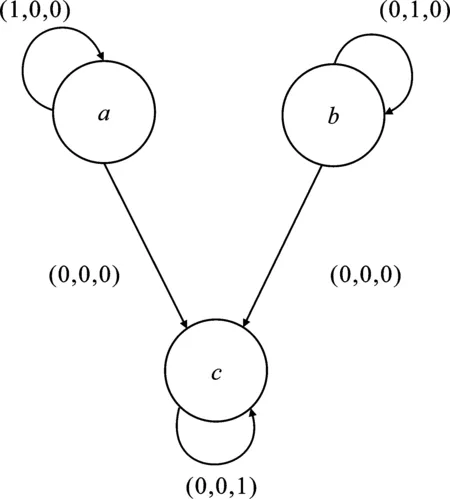
图2 矩阵乘法的依赖图

由图2可知，迭代的标准输出形式可以表示为式(3)。

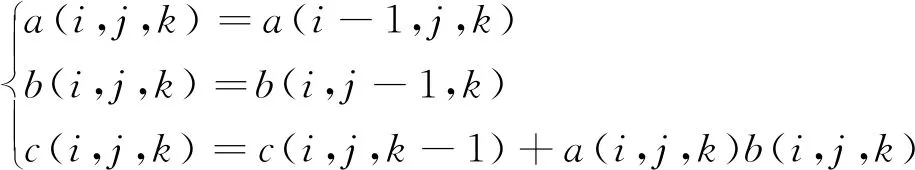
(3)

用于矩阵运算的脉动阵列主要分为一维、二维脉动阵列结构，如图3所示。

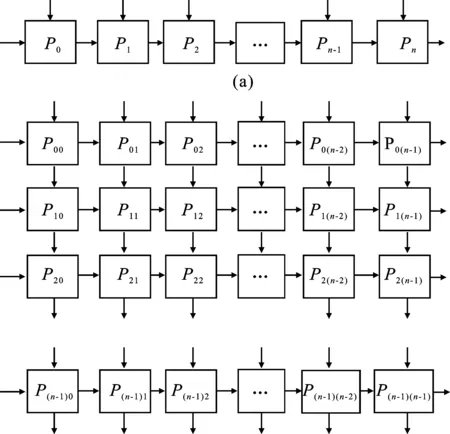
图3 脉动阵列结构图

一维线性阵列可在固定的存储带宽下实现矩阵乘法的加速运算[16]，通过提高运算资源来满足性能需求。相比于一维阵列，二维脉动阵列需要更高的I/O带宽资源，通过增加运算并行度来获得良好的加速性能[17]。结合脉动阵列算法，本文在多核系统中针对不同维度的矩阵乘法实现了多种有效的映射方案，既满足了对不同维度矩阵乘法运算的适应性，又保留了脉动阵列算法卓越的运算性能。

2 基于NoC多核系统

基于NoC多核系统是一种可编程的多核处理系统，主要面向复杂度高、数据带宽要求大的计算密集型应用，如图4所示。

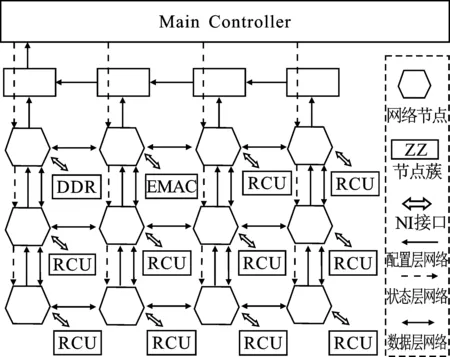
图4 NoC多核系统的结构框图

系统中主要包括主控制器(Main Controller)、NoC网络节点，其节点中挂载了可重构运算单元(Reconfigurable Calculate Unit，RCU)以及外围存储器。NoC网络是整个系统数据传输枢纽，主要负责网络节点间的数据传送。主控制器通过片上网络实现了对节点中运算单元的控制管理，保证了系统高效的数据通信效率。

RCU是一种可重构的计算单元，也是整个多核系统的核心运算单元，支持IEEE 754标准的32位单精度浮点运算能力。在不同配置信息下，RCU可以完成多种规则的单精度浮点运算，包括加、减及乘累加等运算。RCU结构如图5所示。

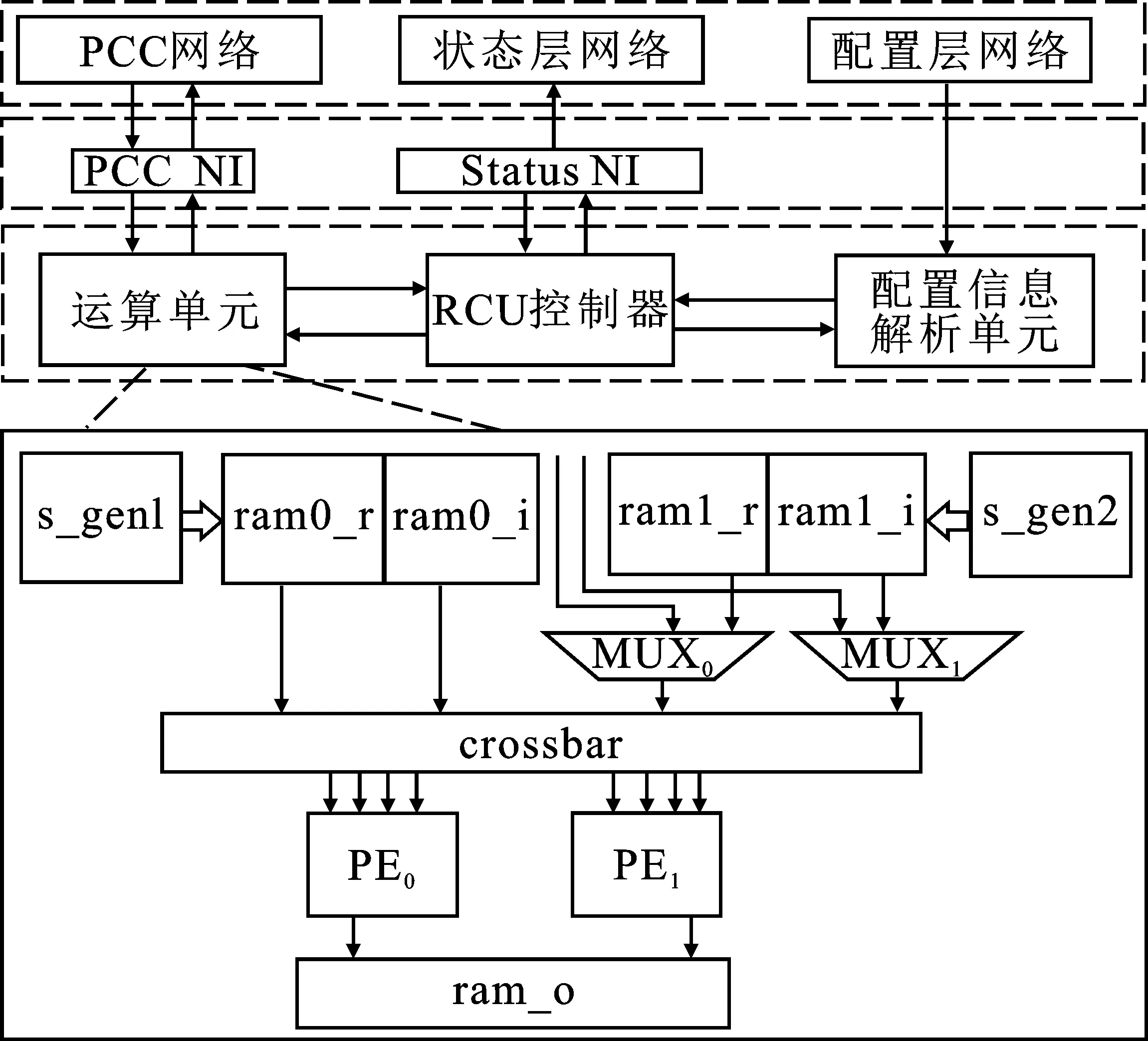
图5 RCU结构图

NoC系统可以支持多种工作模式：流、存储和脉动工作模式。图6为流模式的结构图，结构中两条路径route1、route2分别执行双目运算和单目运算。route1执行xin的数据传递，待xin存入PE(Processing Element)后，yin直接流入PE进行计算，得到计算结果z=z+xin·yin。route2中xin不参与计算，流入PE的值为空值(NULL)。先执行route1，并释放route1执行route2，寄存在PE中的xin作为源数据与新数据yin进行计算，有效提高了数据xin的复用度。

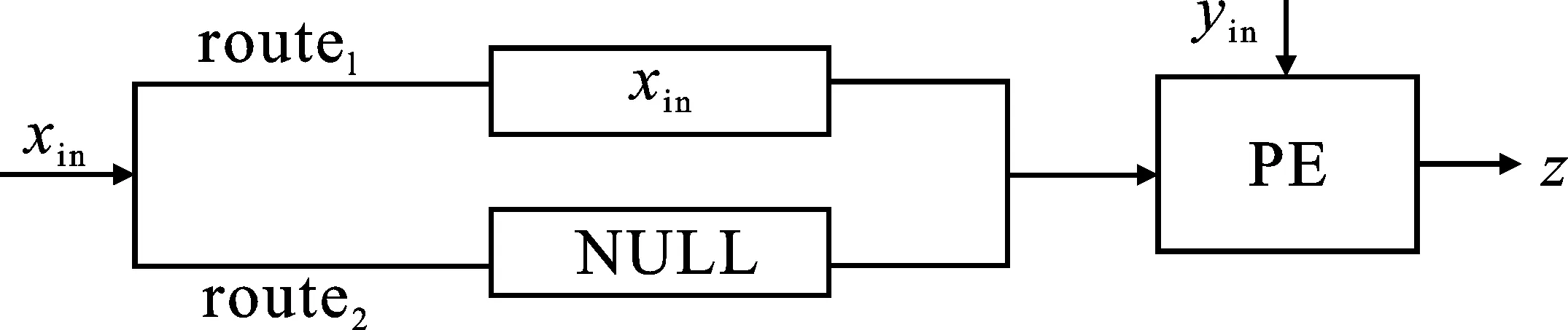
图6 流模式结构图

脉动模式利用了传统脉动算法中数据的流动方式，如图7所示。PE中计算结果z0、z1可以由式(4)表示。

(4)

计算完成后，z0和z1存储在PE中作为下一次计算的中间结果，x0、x1和y0、y1分别流入相邻节点，并以流水线形式进行传递。整个运算阵列可以同步工作，不仅提高了运算并行性，还获得了较高的数据吞吐量。在有限的I/O带宽下，为了保持系统的运算速度与I/O带宽之间的平衡，脉动工作模式较适用于节点数较少的运算阵列。

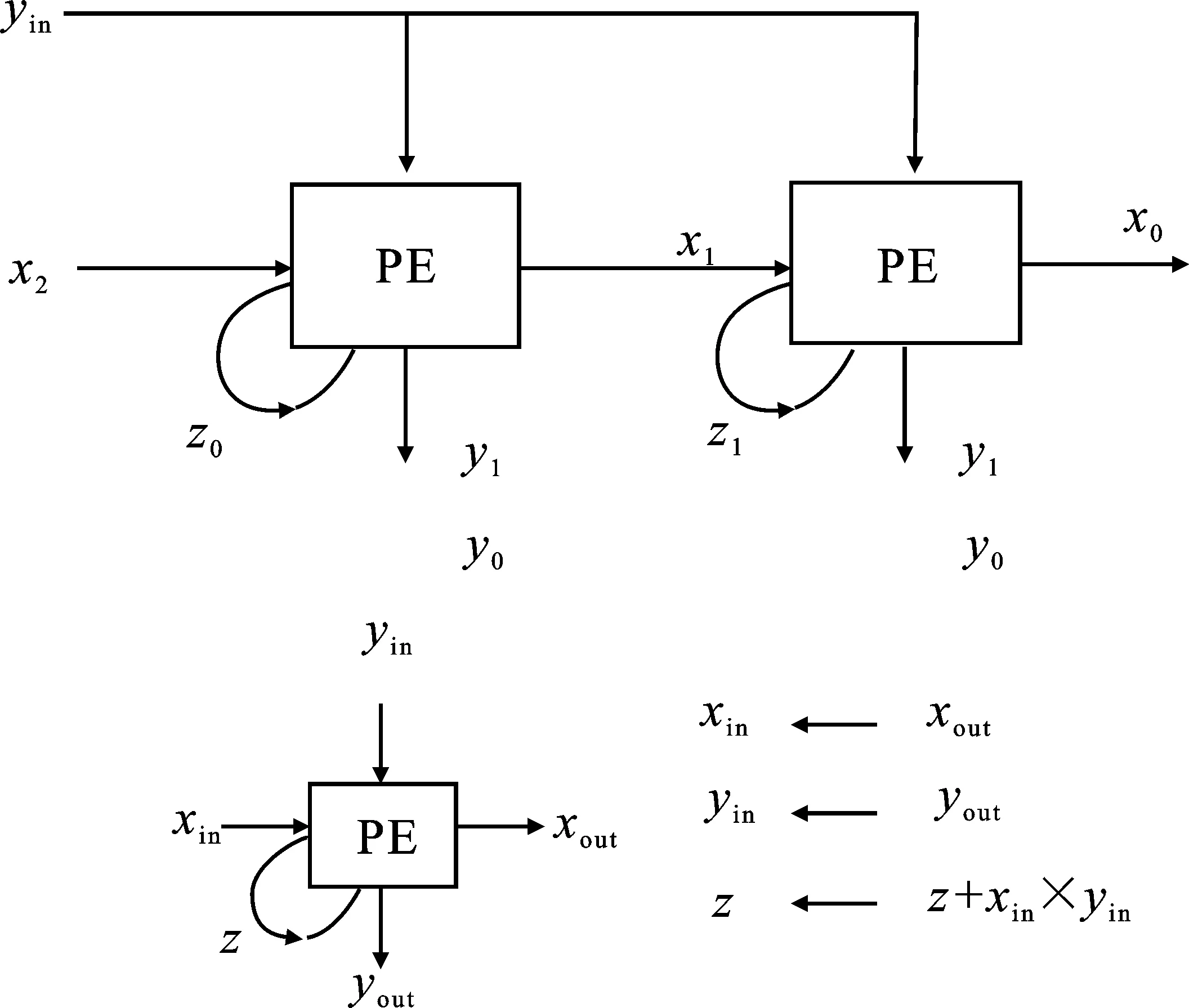
图7 脉动模式结构图

存储模式中数据在运算节点中缓存，通过特殊的地址控制规则对数据进行读写控制，规则如图8所示。

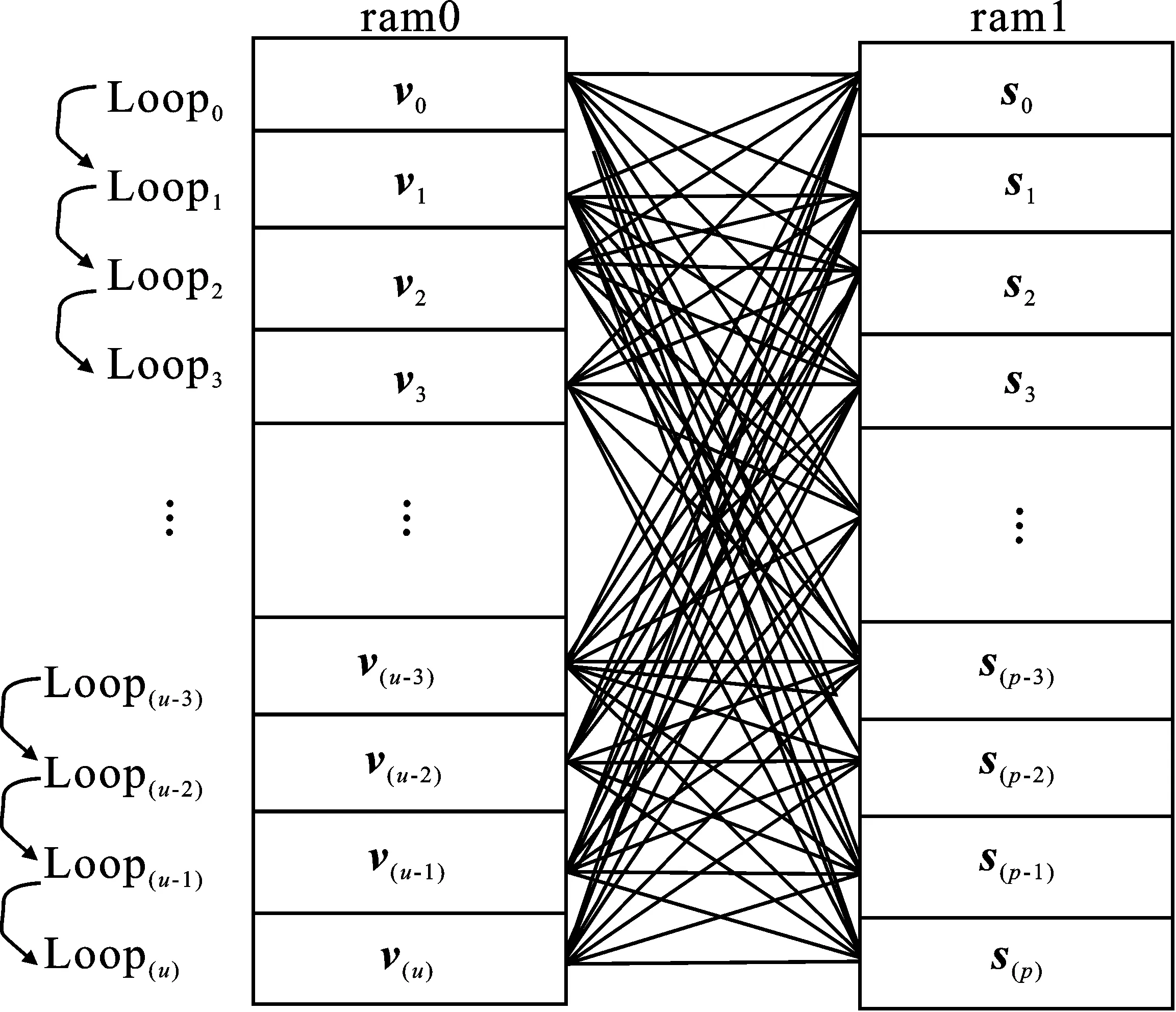
图8 存储模式运算规则

具体代码如下：

输入：矩阵v；矩阵s。

输出：矩阵积h=v·s。

begin

for u=0 to N-1 do

for p=0 to N-1 do

h(u,p)=v(u)×s(p)

end for

end for

end

其中，u、p分别代表ram0中矩阵v行向量和ram1中矩阵s列向量的序列号；N为总向量个数。

该模式下数据可以实现完全复用，提高了数据复用性，减少了重复数据传输带来的周期消耗及I/O带宽占用率，并降低了数据传输周期占总运算周期的比值，可以有效提高系统的计算速度。

本文针对不同维度的矩阵在多种映射方案中灵活运用上述系统的工作模式，提高了矩阵乘法在阵列结构中的运算效率。

3 算法映射

基于NoC多核系统可实现多种运算结构，具有良好的灵活性。本设计分别以I/O带宽和运算资源为设计导向，提出了多种映射算法。

3.1 基于I/O带宽的矩阵乘法

在有限的I/O带宽资源下，确定系统中最大带宽通道的数量，通道数量的计算式如式(5)所示。其中，Q表示最大带宽通道数量；W表示数据位宽；D表示最大可支持带宽；f表示工作频率。该算法通过对不同阵列结构进行合理的带宽分配来提高计算并行度和带宽利用率，如图9所示。

(5)

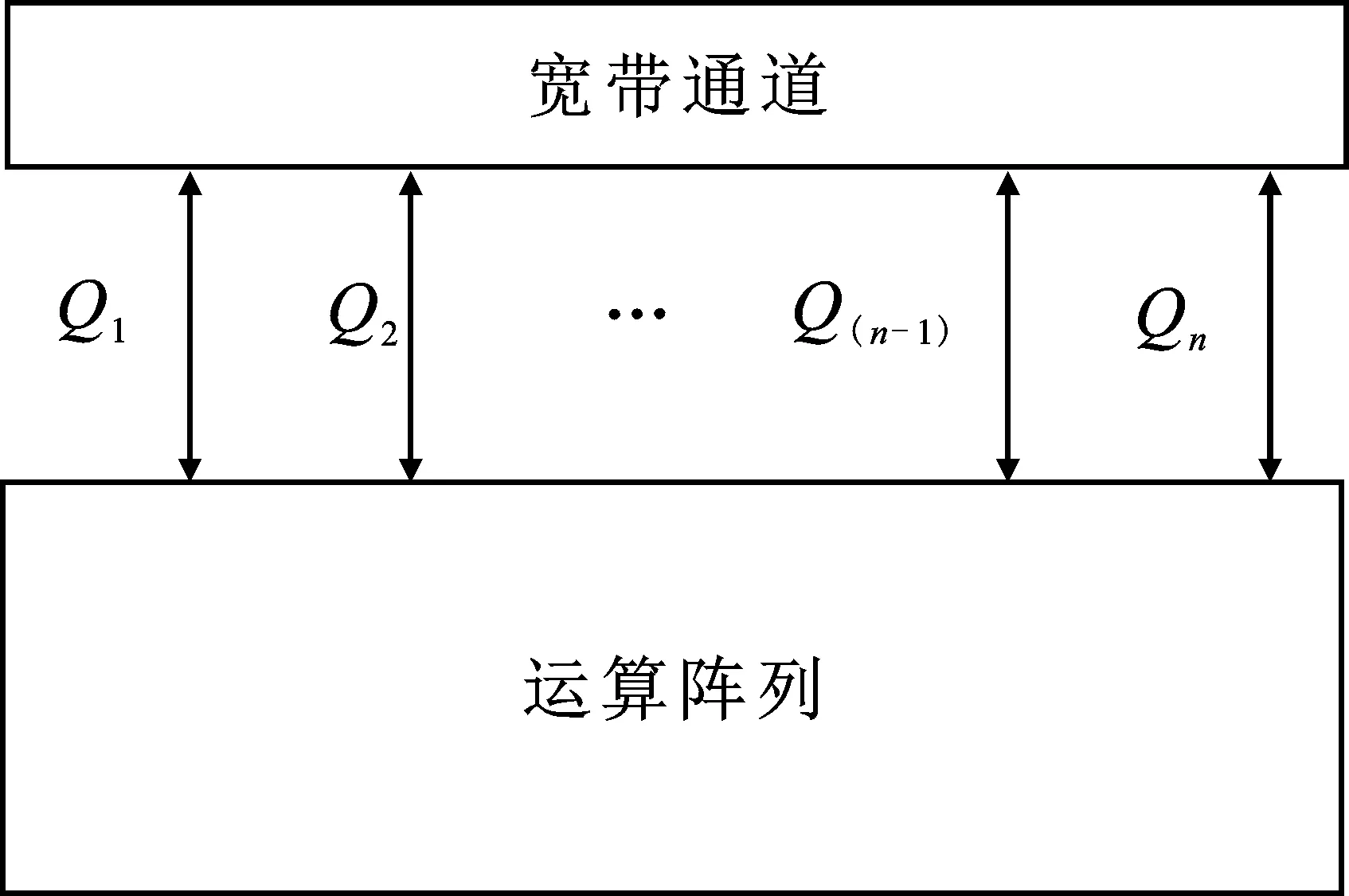
图9 基于I/O带宽的结构示意图

本设计中外围存储接口的数据带宽通道最大可以支持8路并发，基于有限的I/O带宽提出了以下几种映射方案。

方案1该方案采用4×4的运算阵列，如图10所示。

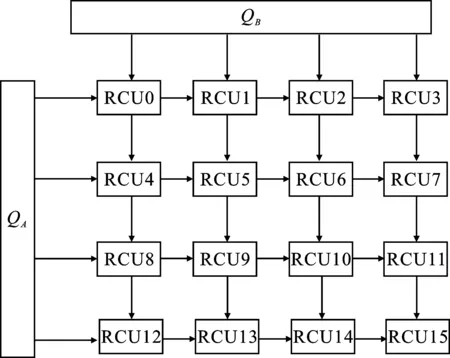
图10 映射方案1

在该阵列中，QA、QB通道分别负责矩阵A和B的数据传输，并通过脉动传输方式在阵列中执行计算。数据在流经阵列的交叉计算节点时实现多次复用，充分保留了脉动阵列高度并行流水的运算形式。计算的结果在RCU内部存储器中缓存，每个RCU可存储2 k点的结果数据。可以看出，方案1中的运算阵列最大可支持32 k点数据缓存，缓解了数据回写引起的带宽负担。但当矩阵维度大于128时，本地数据缓存空间不足，需要额外的带宽用于数据回写，导致乘法器中的计算单元出现空闲状态，影响系统整体的计算性能。

方案2在方案1的基础上进行折叠、展开，得到方案2，其结构如图11所示。

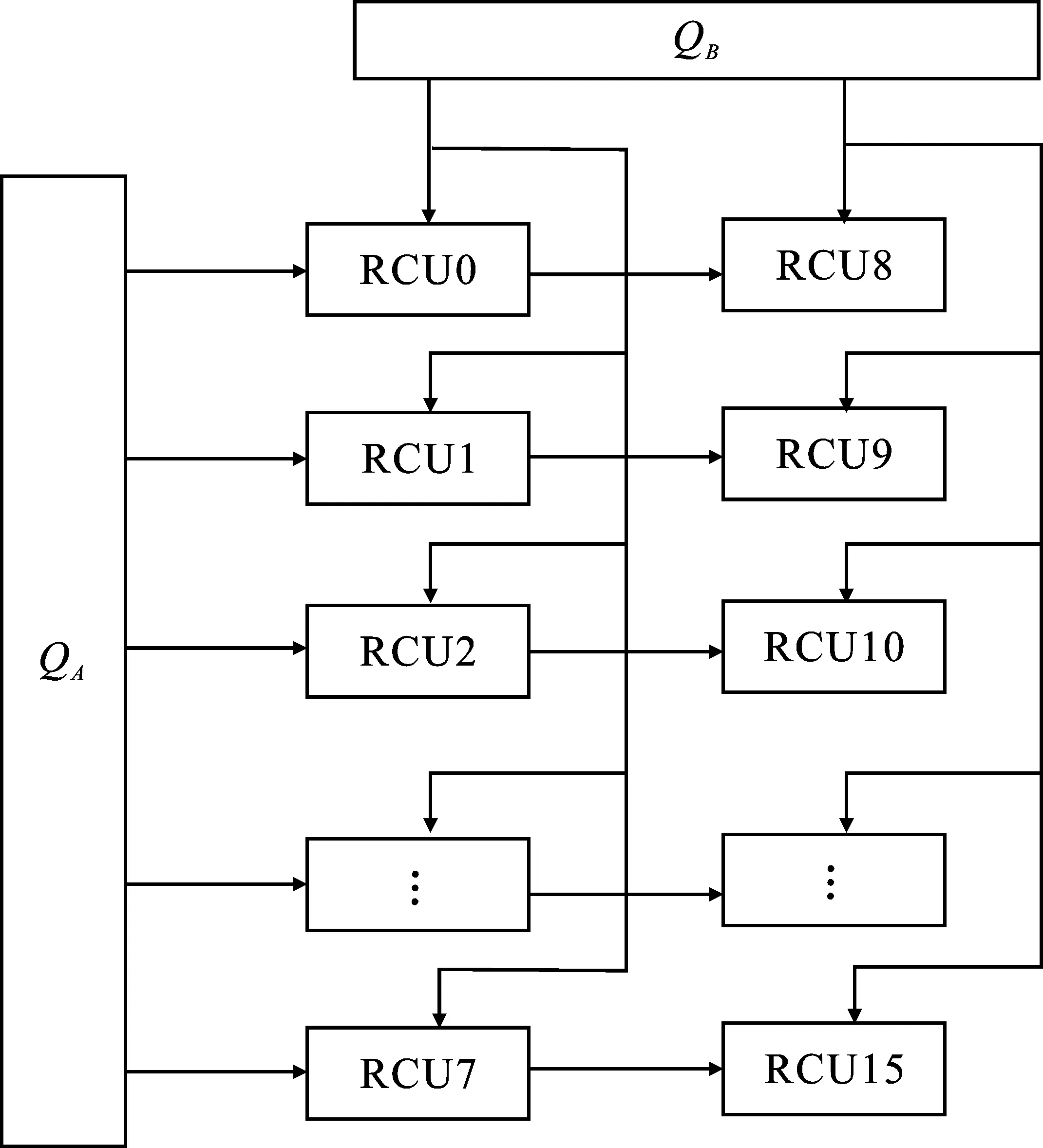
图11 映射方案2

该结构为双阵列结构，主要分为task1、task2两个任务过程。task1如下：QB通道以广播的数据传输形式向两列运算单元发送矩阵B的列向量元素，待数据传输完成后，释放QB通道，执行task2。task2为：QA通道发送矩阵A的行向量元素，并采用存储模式在RCU节点中完成向量乘运算，得到的计算结果在本地缓存，直至完成矩阵的所有运算，输出结果矩阵。

在处理阶数不大于64的矩阵乘法时，相比于方案1，方案2中数据的分配控制相对简单，并且可以实现数据的完全复用，有效地减少重复数据传输次数，降低了运算节点的闲置率。当矩阵维度处于64～128之间时，矩阵B通道的传输次数增加，但并不影响整个结构的并行运算形式。当维度大于128时，本地空间不足导致阵列单元的闲置率增大，系统的运算性能受到影响。

3.2 基于运算资源的矩阵乘法

方案3随着矩阵规模的进一步增大，仅仅利用有限的I/O带宽来提高矩阵乘法的运算速度是不够的。在具有充足的运算资源下，上述两种映射方案由于受到I/O带宽的限制，运算资源将成为大维度矩阵乘法运算的瓶颈。为了提高运算结构的可扩展性，系统采用固定带宽数量为Qs(Qs=QA+QB+QC=3)的线性阵列结构。该结构可以将NoC系统中挂载的所有计算节点连接在一起，并且不受I/O带宽的影响，如图12所示。

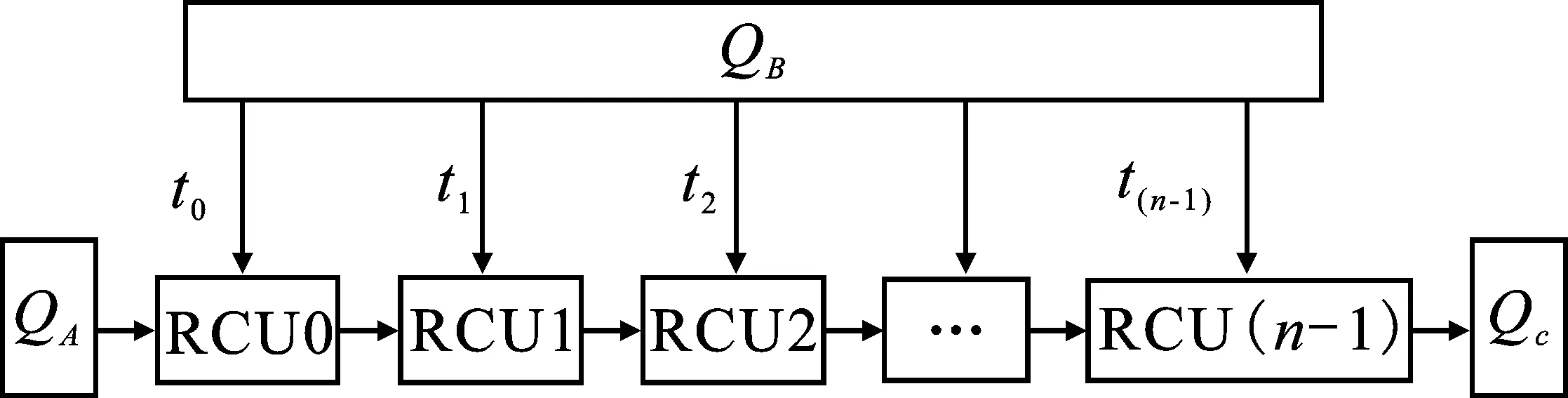
图12 映射方案3

在该方案中，QA通道通过线性阵列传递矩阵A的数据，QB通道采用单通道的分时传递方式。t0时刻，完成第n=0个RCU节点的数据传送；t1时刻，完成第n=1个RCU节点的数据传输，此时第n=0个RCU节点中通过流工作模式与流经该节点的数据进行计算；tn时刻，其中tn=t(n-1)+1，结束第n-1个RCU节点的数据传输，并重新向第n=0个RCU节点发送数据。这种传输方式提高了运算结构的可扩展性，保证数据的高效复用和并行流水的运算机制。同时，针对大维度的矩阵乘法，可以在更低的I/O带宽要求下调度当前系统中所有的运算资源，相比方案1和方案2，该方案预留了数据结果的回写通道Qc，解决了大维度矩阵运算中由于I/O带宽、存储空间不足而导致的运算节点的闲置问题，能够有效提高大规模矩阵乘法的运算速度。

4 实验和结果分析

本实验在Xilinx公司Virtex7系列XC7V2000T FPGA芯片上进行原型验证。RCU内部PE单元的浮点乘法器和加法器使用Xilinx公司提供的Floating Point IP核实现。本设计中所使用的FPGA开发环境和仿真环境为Xilinx Vivado 2018.3及MentorGraphics Modelsim SE-64 10.2c。

4.1 系统的峰值计算性能

理想情况下，系统中RCU单元每个周期可以完成1次单精度浮点乘法和1次单精度浮点加法操作。系统的计算性能可由式(6)得出

PERFpeak= 2×(P×f)

(6)

式中，PERFpeak表示矩阵乘法器的峰值计算性能(每秒百万次浮点操作)；P为RCU节点的个数；f为矩阵乘法器工作的时钟频率。各映射方案的FPGA内部资源使用情况如表1所示，该乘法器在未作优化的情况下工作频率为158.7 MHz。由此可以得出该系统的峰值计算性能可以达到5 078 MFLOPS。

表1 FPGA内部资源消耗表

4.2 系统对不同规模下矩阵乘法的性能分析

表2为系统中在不同规模下矩阵乘法的运算周期，为了方便对比，脉动阵列中由16个运算单元组成的4×4阵列。

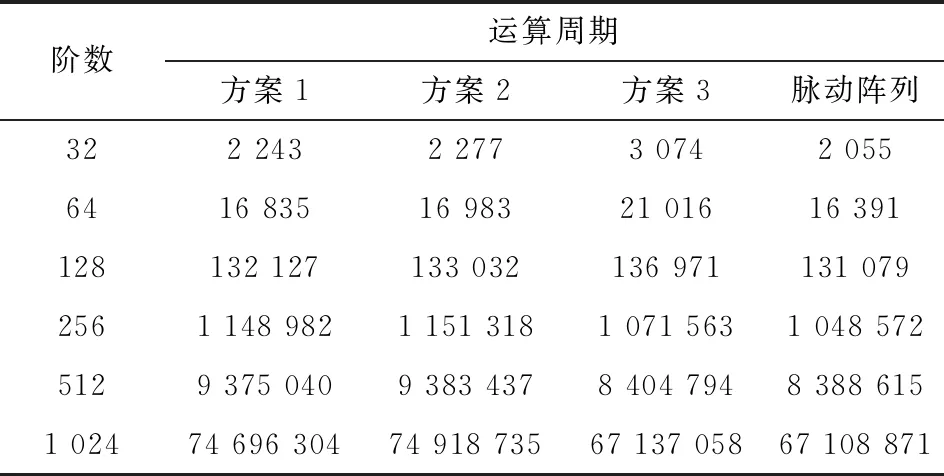
表2 不同矩阵乘法的运算周期

由表2中的实验结果可以看出，当矩阵阶数不大于128时，方案3的运算消耗的周期数最大，高于方案1和方案2的周期数。当阶数大于128的矩阵乘法时，方案3的运算周期消耗最小，并逐渐与脉动阵列的运算周期相近。

为了方便对实验结果的进一步分析，以不同映射方案的运算并行度更直观地表示系统的运算性能，其中并行度定义计算式为

(7)

式中，Ep表示并行度；Sp表示加速比；Ts表示串行算法的计算时间；Tq表示在q个运算节点下的计算时间；q表示计算节点个数。各映射方案的计算并行度如表3所示。

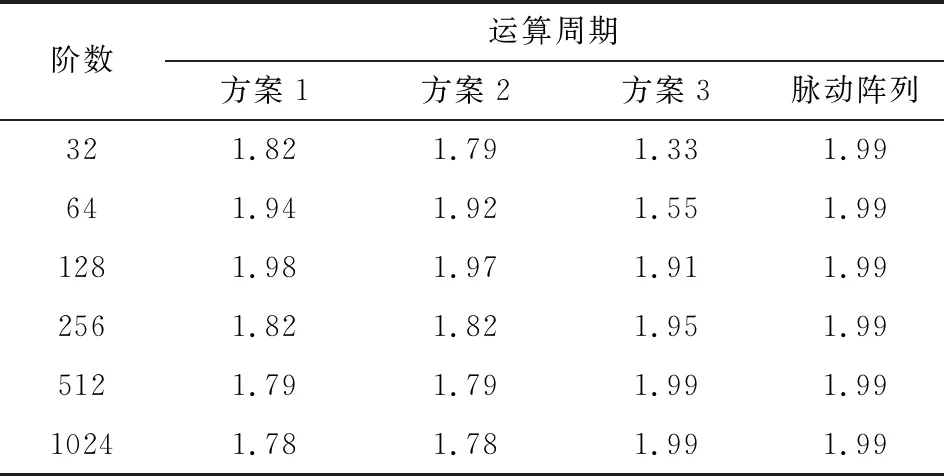
表3 不同映射方案的运算并行度

由表3可知，矩阵阶数小于128时，方案1和方案2的运算并行度高于方案3，并逐渐趋近于脉动阵列的运算并行度。当矩阵阶数大于128时，方案1和方案2的运算并行度不断下降。而随着矩阵维度的不断增大，方案3运算并行度不断提高，最终达到脉动阵列的运算并行度，并保持不变。

可以总结出，在处理规模相对较小的矩阵乘法时，方案1和方案2高度并行的数据传输和运算形式有效提高了矩阵乘法的运算速度，并获得了较高的运算并行度。但随着矩阵规模增大，方案1、方案2中存储容量和带宽资源达到上限，数据回传周期占总运算周期的比例越来越大，导致运算速度受到限制，并行度也随之降低。此时方案2的数据传输周期占总周期的比例会越来越小，运算节点的闲置率最低，并保持高度并行全流水的运算形式，从而获得了良好的运算性能。

5 结束语

本文通过对矩阵乘法硬件加速常规算法的分析，设计了一种基于NoC多核系统的矩阵乘法器，并在Xilinx XC7V2000T FPGA上进行了实现。该矩阵乘法器不仅可以利用系统可重构性针对具体的性能需求灵活地改变运算结构，提高矩阵乘法器的通用性和可扩展性，还保留了脉动阵列算法中高度并行的运算形式，取得良好的运算性能。系统整体的运算性能仍有较大的提升空间。为了获得更高的并行度和运算速度，可以增加存储资源、I/O带宽以及运算节点个数，也可以进一步改善和增强RCU的运算性能，提出更高效的映射算法来提升矩阵乘法的运算速度。