一类具有分布时滞的离散SVIR传染病模型的稳定性分析

许泽宇，雒志学

（兰州交通大学数理学院，兰州 730070）

近些年来，为了能更加准确地描述传染病的传播机理，引入了时滞这一概念。在传染病的研究过程中，大量学者发现时滞能够破坏模型的稳定性，并在一定条件下产生Hopf分支。通常用微分方程建立的模型都是连续的［1-13］，对离散模型的研究比较少，而且离散模型在参数和初值的选取上都相对容易。因此建立和分析离散传染病模型更具有实际意义。在考虑具体的传染病模型时，大多数模型采用的是标准发生率和双线性发生率。为了方便起见，本文选取传染病模型中经常使用的双线性发生率。

1 模型的建立

Li等［14］研究了一类具有双线性发生率的SVIR传染病模型，即：

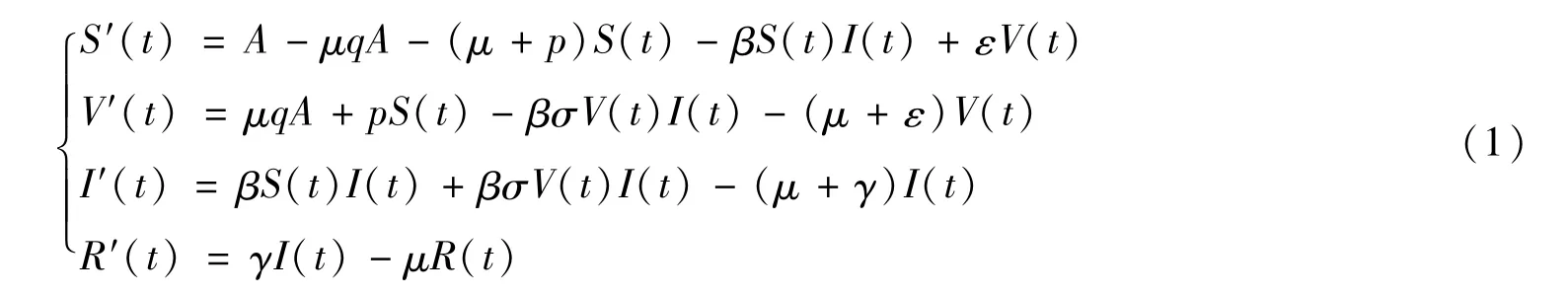
该模型给出了无病平衡点全局渐进稳定和地方病平衡点局部渐进稳定所满足的条件。若潜伏期比较小时，则地方病平衡点是全局稳定的。

对模型（1）进行降维，则它的等价系统为：

在系统（2）的基础上考虑分布时滞对传染病的影响，建立了如下模型：

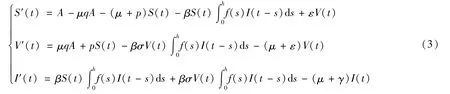
式中：S（t）、V（t）、I（t）和 R（t）分别表示 t时刻易感染者、接种者、染病者和恢复者的数量；A表示易感染者的输入量（包括新生儿）；假设上述4类人均具有相同的死亡率μ（0≤μ≤1）；q（0≤q≤1）表示新生儿的疫苗接种率；p（0≤p≤1）表示易感染者的疫苗接种率；β和βσ（0＜σ＜1）分别表示传染病在易感人群和接种人群中的传染率；ε表示免疫失效比例；γ表示感染者的恢复率；h（h＞0）表示时滞；f（s）≥0且满足且上述参数和变量均为非负数。

传染病的传染机制如图1所示。

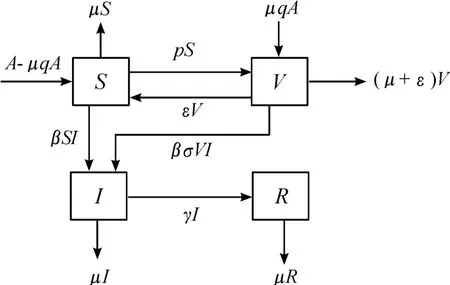
图1 传染病的传染机制示意图

为了便于讨论，采用隐式Euler方法对系统离散化后进行研究，主要思想是应用文献［15-16］的方法处理该离散传染病模型，运用隐式Euler方法建立系统（3）所对应的离散传染病模型：

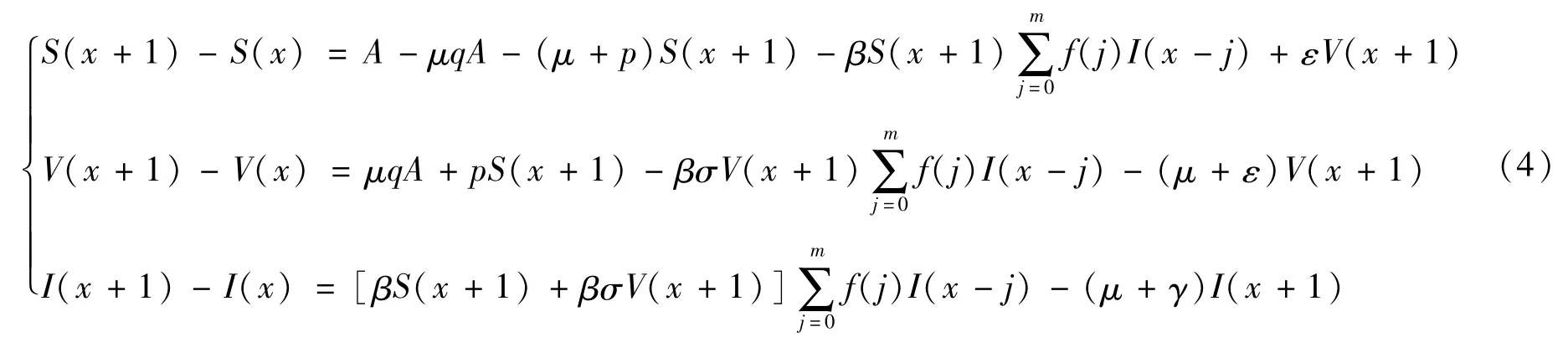
初始条件为：

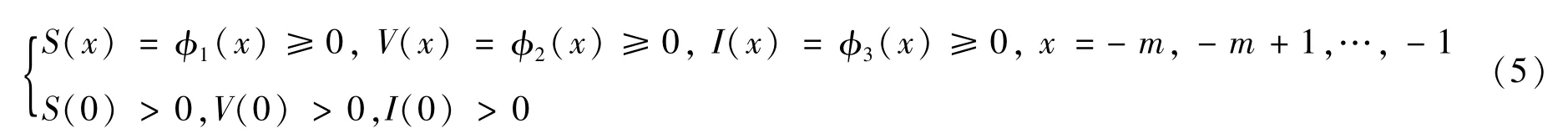
当 I（x）≡0时，容易得到系统（4）的无病平衡点 E0＝（S0，V0，0），其中：

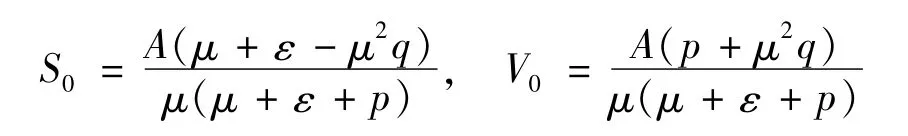
定义基本再生数为：

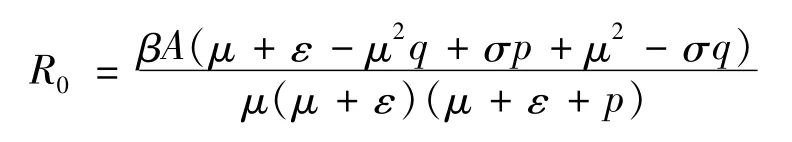
2 无病平衡点的全局吸引性

引理2.1［17-19］当 x＞0时，系统（4）的任意解（S（x），V（x），I（x））都满足 S（x）＞0，V（x）＞0，I（x）＞0。

定理2.1若R0＜1且γ＞μ+2ε，则系统（4）的无病平衡点E0是全局吸引的。

证我们利用文献［20］中的方法来定义Lyapunov函数，有：

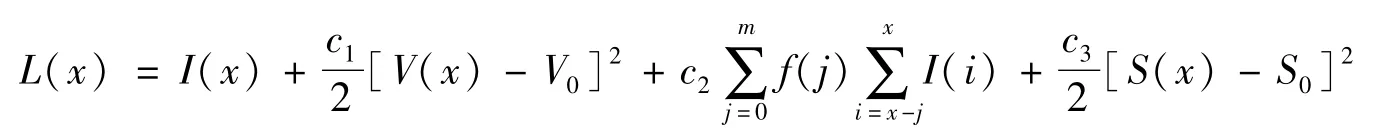
记

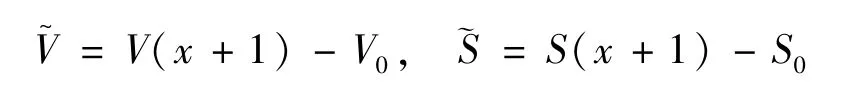
根据引理［2.1］可知 I（x）＞0，从而 L（x）＞0，即 L（x）正定。

由系统（4）可以得到：

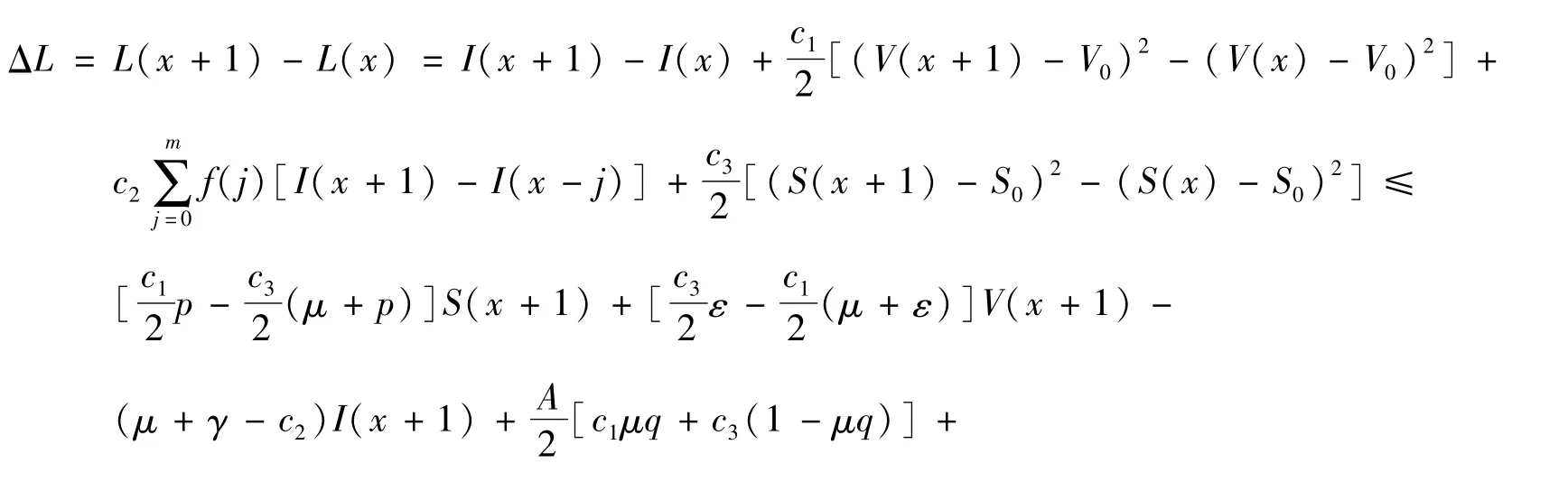
要使 ΔL＜0，只需找到 ci（i＝1，2，3）＞0，使下面的条件同时成立：

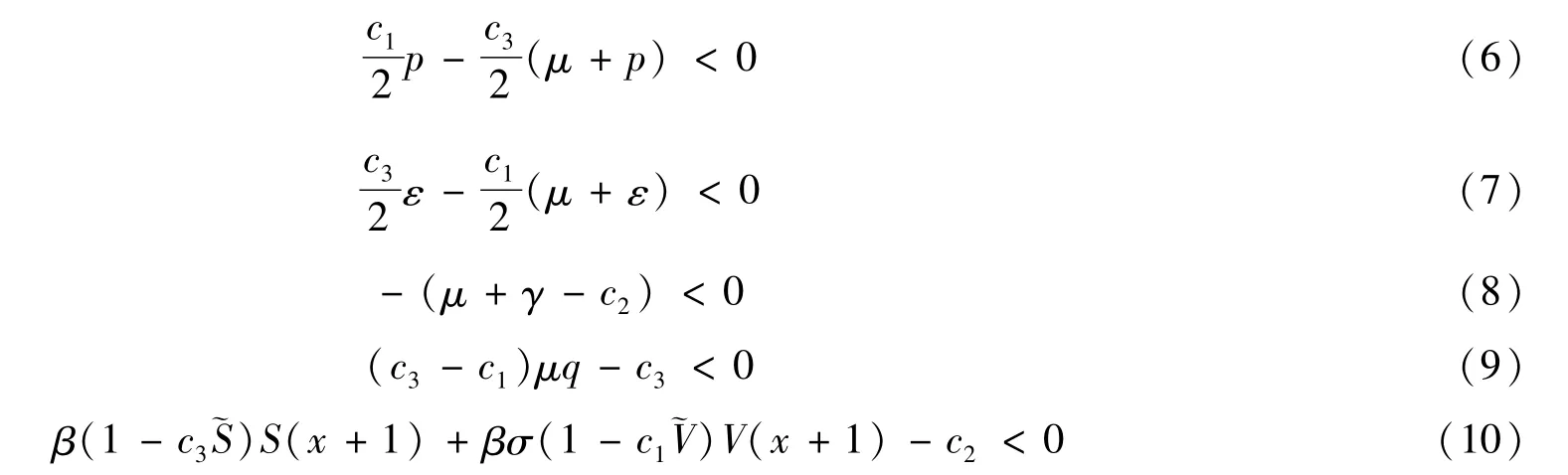
联立式（6）和式（7），可以得到：

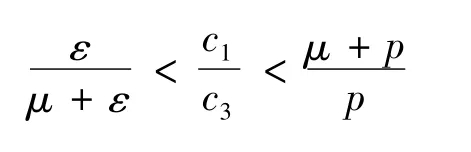
由式（8）可得：

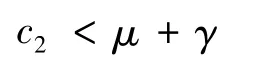
因为 μ，q∈［0，1］，所以 μq-1≤0，从而对于任意的正数 c1和 c3，式（9）恒成立。

式（10）可以变形为：

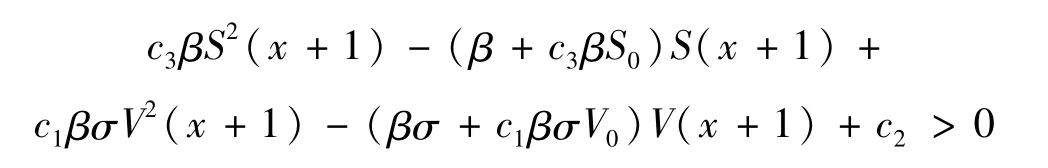
根据实际意义，式（10）等价于：

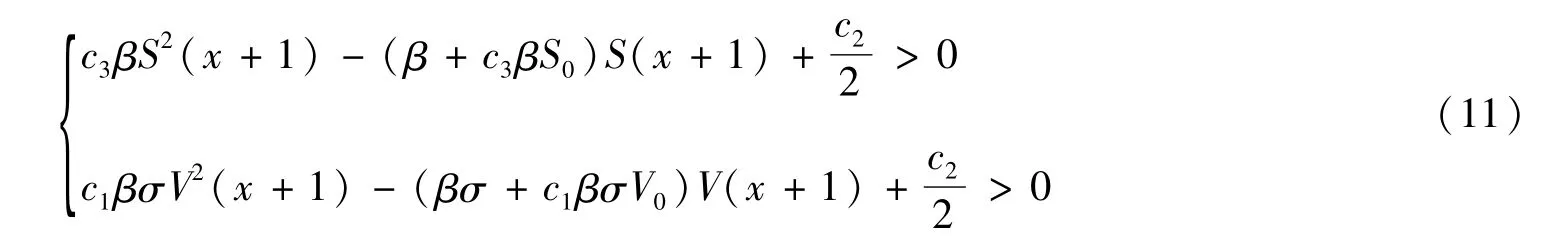
已知c3β＞0，要使式（11）的第一式成立，则只需：

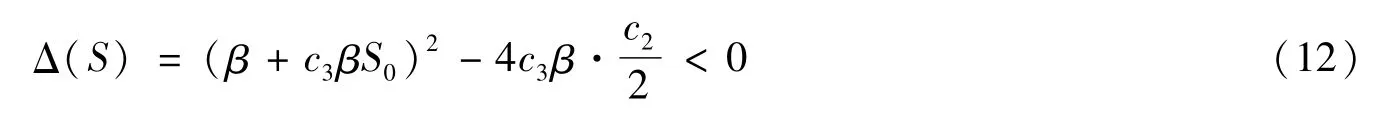
将式（12）关于c3展开，有：

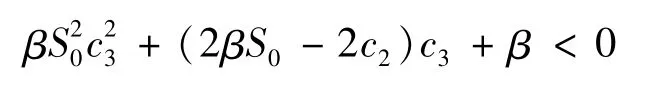
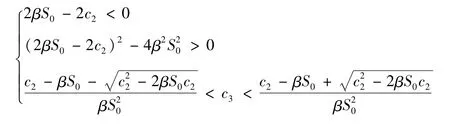
即

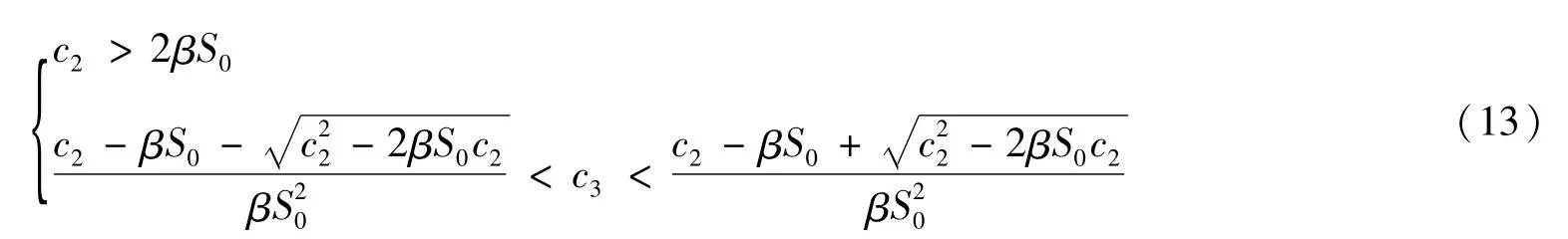
同理，可以找到使式（11）的第二式成立的条件，有：

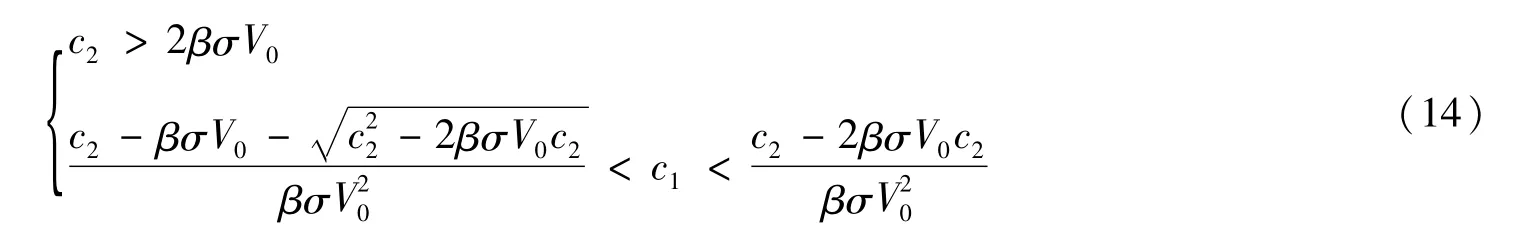
因此，当式（13）（14）同时成立时，式（10）成立。

综上所述，只需逐次找到c2、c3、c1满足如下条件：

由于 R0＜1，由此可知 βS0＜μ+ε，βσV0＜μ+ε，则式（15）成立需满足 γ＞μ+2ε。综上讨论，依次取：

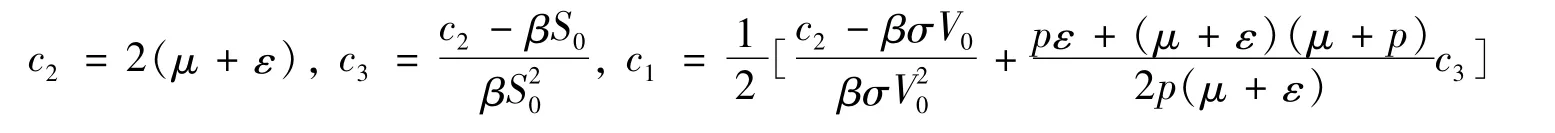
使式（6）～式（10）同时成立，最终使 ΔL＜0。因此数列｛L（x）｝单调递减且有界，从而｛L（x）｝收敛，即：

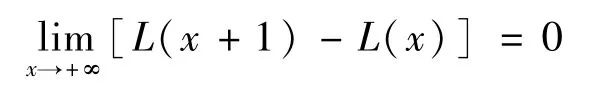
则有

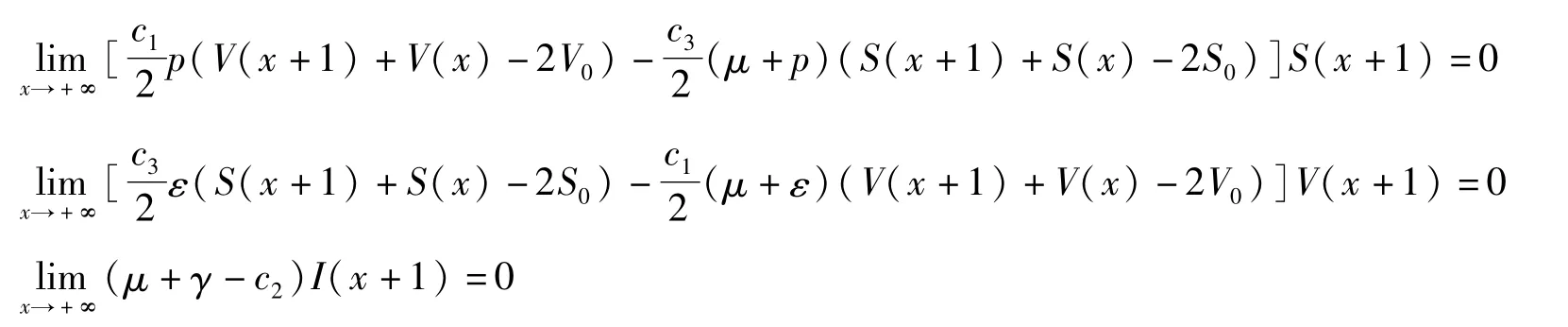
所以

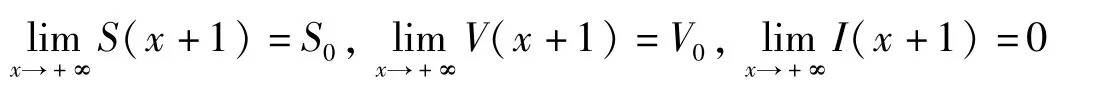
3 系统的持续性

引理3.1若系统（4）的任意解为（S（x），V（x），I（x）），记总人口为 N（x）＝S（x）+V（x）+I（x）+R（x），则有

证由系统（4）可以得到：

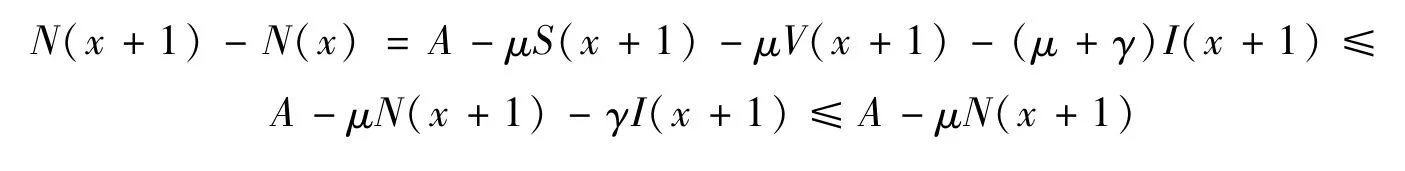
故有

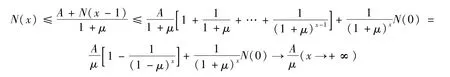
定理3.1若 R0＞1，则系统（4）对任何初始条件（5）是持续的。

证根据引理［3.1］可知，对任意的 ε0＞0，存在充分大的 x0＞0，当 x＞x0时，有

由系统（4）的第一式可得：

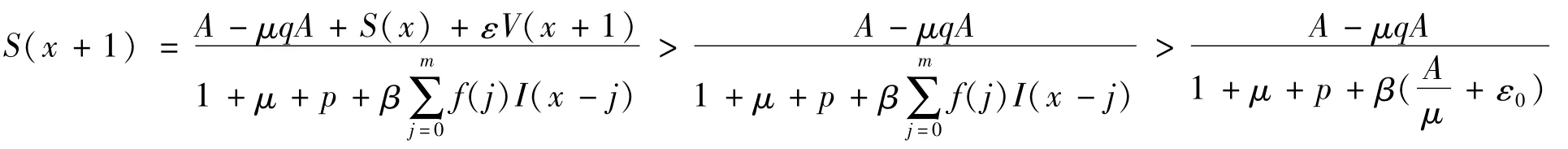
由ε0的任意性可得：

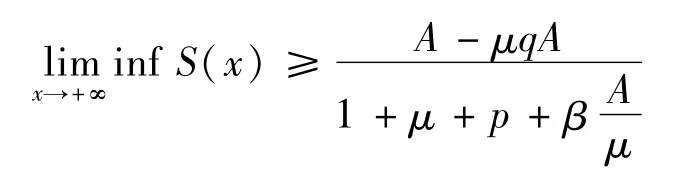
因此由引理［3.1］有：

同理，由系统（4）的第二式可得：

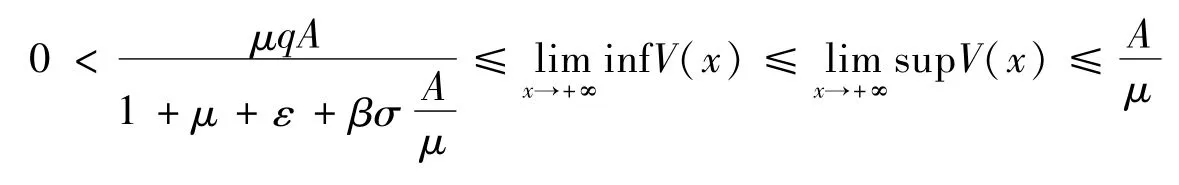
由于

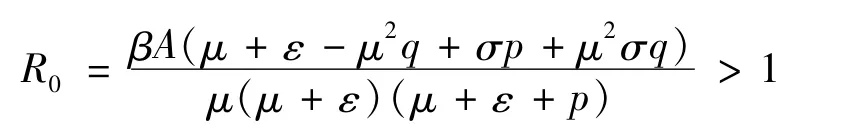
则存在0＜α＜max｛I（x）｝和θ＞0使得：

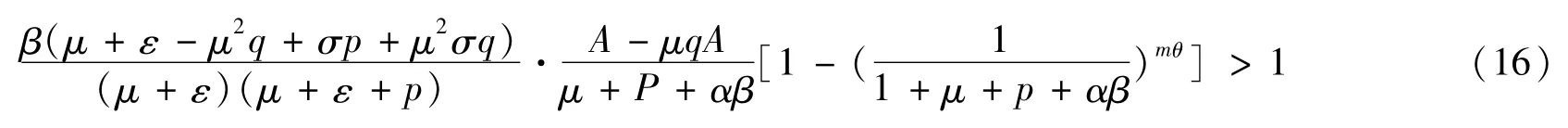
记

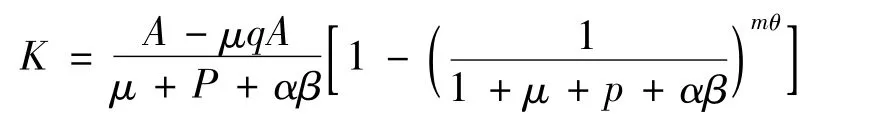
在这里，I（x）和α的关系只能有以下3种情况：

（i）对于任意的 x＞mθ，都有 I（x）≤α；

（ii）对于一切充分大的 x，都有 I（x）＞α；

（iii）当 x充分大时，I（x）关于 α振荡。

根据系统（4）中第三式的特点，构造数列：

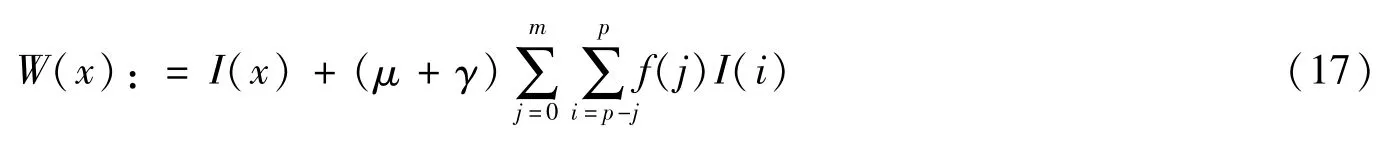
则

当x≥x1+m时，有：

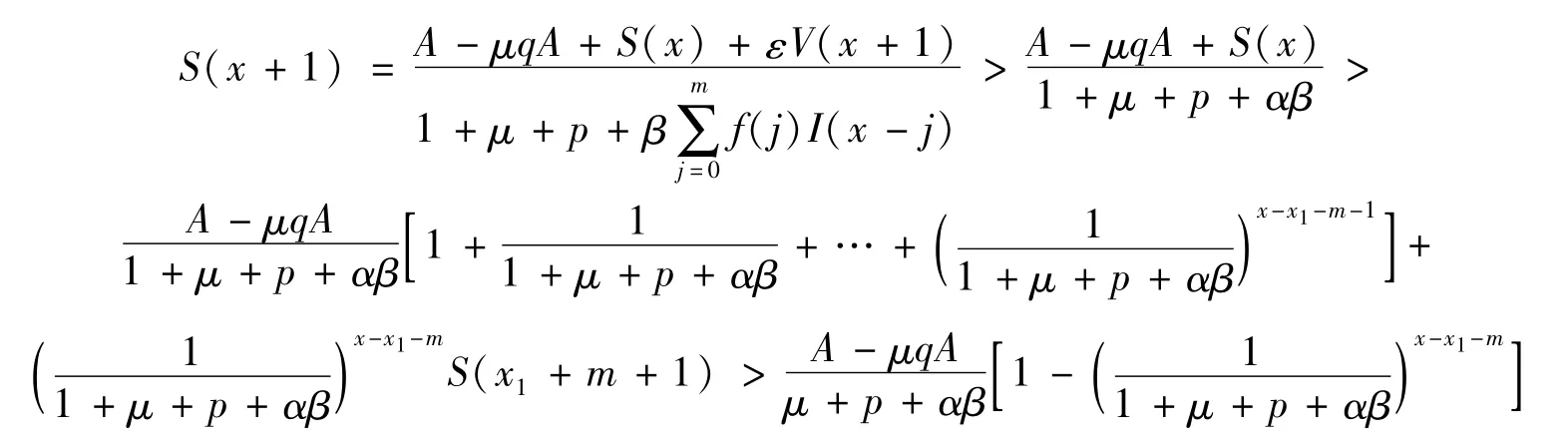
当 x≥x1+m+mθ时，有：

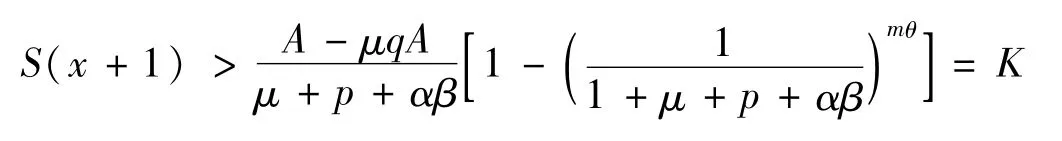
同理有：

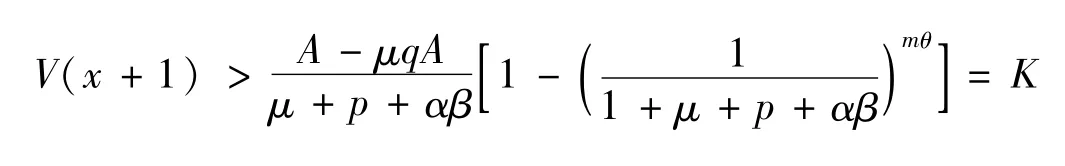
因此

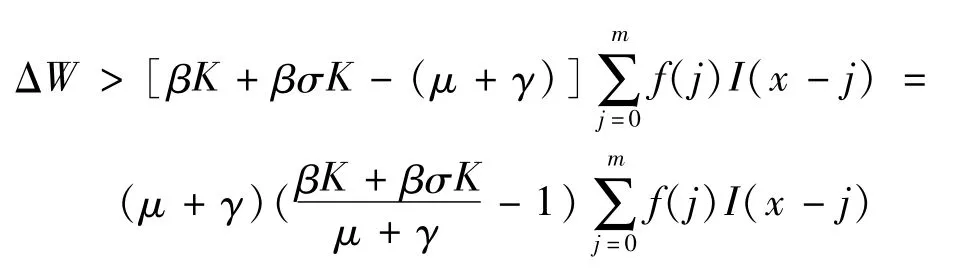
设 I′：＝min｛I（x1+mθ+2m+k）｝，k＝-m，-m+1，…，1，0，则，当 x≥x1+m+mθ时，I（x）＞I′。

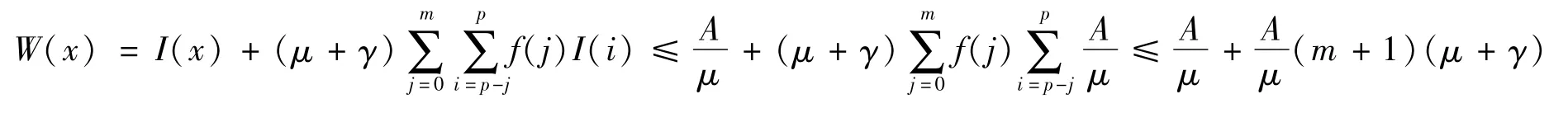
即W（x）有界，这与 W（x）→ +∞矛盾，故情况（i）不成立。

若情况（ii）成立，则结论成立。

若情况（iii）成立，设存在足够大的 x，x1，x2满足 x1＜x＜x2，使 I（x1），I（x2）≥α，I（x）＜α，由系统（4）可知，I（x+1）-I（x）≥ -（μ+γ）I（x+1），即对任意的 x1＜x＜x1+m+mθ，都有：

如果x2≥x1+m+mθ，则用相同的方法可以得到由区间x1＜x＜x2的任意性可知，对足够大的x都有即得到：

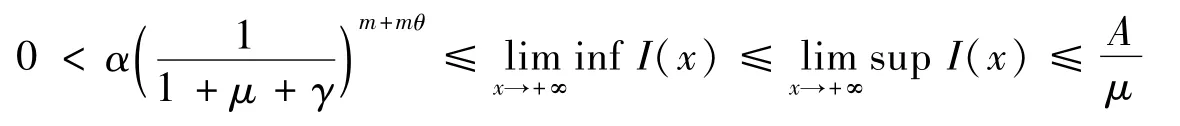
综上所述，系统（4）对于任何初始条件（5）是持续的。

4 结论

考虑了一类具有分布时滞的离散SVIR传染病模型，从理论上分析了该模型的动力学性质。首先对原模型等价降维，得到了连续的模型；然后运用隐式欧拉方法对模型离散化，并通过计算得到系统的无病平衡点E0和基本再生数R0；最后证明了无病平衡点的全局吸引性和系统的持续性。最终得到如下结论：当R0＜1时，系统的无病平衡点E0是全局吸引的，疾病会消亡；当R0＞1时，系统是持续的，疾病将始终存在。通过对这种SVIR模型的研究，给该类传染病的预防和控制提供了理论基础，具有一定的参考价值。