基于改进Bingham模型的磁流变阻尼器力学建模及试验研究

祝世兴，杨丽昆，魏 戬，祝恒佳

（中国民航大学航空工程学院，天津 300300）

磁流变阻尼器（magnetorheological damper，MRD）是一种阻尼可调的半主动智能控制器件，其传动介质磁流变液（magnetorheological fluid，MRF）是一种受磁场影响的特殊材料［1］。MRF的黏度可随外加磁场强度不同而迅速发生变化，进而改变输出阻尼力的大小。因此MRD的输出阻尼可以在外加磁场（一般通过电流大小来控制）作用下实现动态调节，并以其结构简单、可调范围宽、响应快、可靠性和适应性强等优点被广泛应用于建筑［2-4］、汽车［5-8］、航空［9-10］、航海［11-12］等领域。

一般阻尼器多应用于结构的减震、隔振及减摆等维持系统的稳定性方面。在削弱振动过程中往往由于非线性因素［13］（本文MRD的非线性因素主要是MRF）的存在，使系统的运动具有非线性特性，非线性特性对多体系统动力学建模［14-15］的影响是不可避免的。黎崛珉等［16］研究了刚度非线性与阻尼非线性对隔振系统的影响。姚文莉等［17］将非理想系统的动力学建模问题描述为目标函数为高斯拘束函数、优化变量为质点加速度的约束最优化问题，并验证其方法的有效性。Zhu［18，19］等人研究了带有阻尼器的空气弹簧非线性动力学模型，用来描述车辆减震系统以提高乘坐舒适性。

为了准确模拟MRD复杂的非线性阻尼力特性，实现对MRD精准控制，研究人员基于多体动力学［20］及MRF的材料特性对MRD的力学建模方法进行了深入探究［21-22］。Shou［23］、李赵春［24］等人研究了MRD在冲击载荷作用下动力学响应特性模型。Ma［25］、Gurubasavaraju［26］、Yang［27］等研究了MRF剪切应力模型，对MRF电导率特性进行了 实 验 研 究。Zolfagharian［28］、Peng［29］、陈 世嵬［30］等人对MRD进行参数化建模并对模型的参数辨识方法进行了研究。龚微［31］等提出了一种可以求解阻尼器逆模型的3段线性变阻尼恢复力模型，适用于MRD控制器的设计。梅真等［32］对MRD进行动力性能测试，建立了参数化模型和非参数化模型，通过对比2种建模方式的结果，发现非参数化模型的精度高于参数化模型。

以上研究结果表明，由于MRF的流变机理复杂，目前尚无统一、精确的力学模型描述，使得参数化模型的建模方式复杂化。非参数化模型是基于实验测试结果建立的，利用数值计算方法对模型参数进行辨识，得到较为精确化的模型，可简化建模方式和提高模型精度。孔祥东等［33］提出了Bingham-多项式力学模型，并与试验测试结果进行对比，解决了Bingham模型精度低、多项式模型高阶不稳定的问题。祝世兴等［34］提出用傅立叶级数来表达MRD的非线性关系，改进了线性模型精度差的问题。刘永强等［35］提出一种对MRD模型进行参数辨识的新方法，分析模型参数对MRD输出阻尼的影响规律，获取调控阻尼力的最佳参数，并拟合参数值和电流之间的函数关系。胡海刚等［36］提出一种将遗传算法和最小二乘法相结合的方法，对MRD的力学模型进行参数辨识，并用Simulink工具箱进行仿真验证，所得结果精度较高，可靠性满足要求。周勇等［37］提出一种改进型RBF神经网络模型，基于实验实测结果，利用线性插值法建立模型算法，并与改进前的模型进行对比，发现改进后模型精度更高，可以更加可靠地描述MRD的动力学特性。

现有的非参数化模型参数较多，建模方式较为复杂，分段模型存在分段方式模糊、拐点不明确等问题。为了精确描述磁流变阻尼器在不同电流下力与速度之间的非线性关系、减少力学模型参数、简化分段模型的分段方式，本文作者通过对台架试验的实验结果进行分析，建立Rational-Bingham模型，采用最小二乘法对模型参数进行辨识，基于台架试验结果对Rational-Bingham模型和多项式-Bingham模型的精度进行对比研究。

1 实验

实验所采用的磁流变阻尼器结构原理图如图1，其中缸筒内填充MRF。

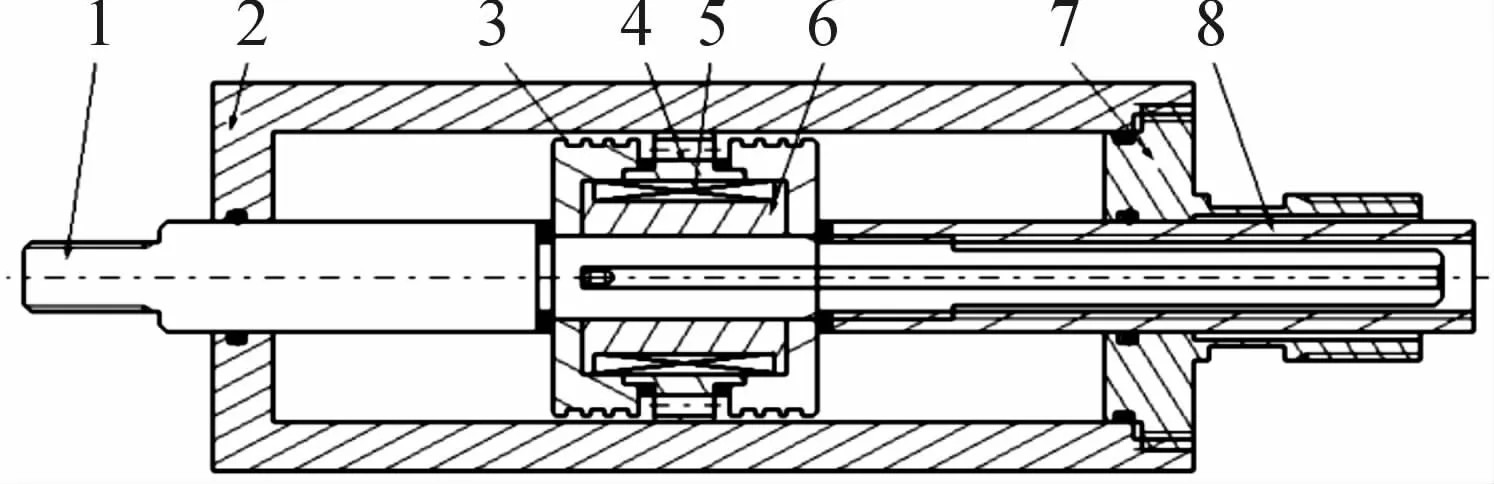
图1 磁流变阻尼器结构原理图

MRD实物图如图2，通过活塞杆引出的导线可以为MRD施加不同大小的电流。阻尼特性测试平台如图3所示，将MRD的上端固定，下端活塞端连接激振台中心，激振台通过液压作动为阻尼器提供正弦位移激励。

实验采用正弦位移激励，以振幅为2 mm、频率为3 Hz为例，通过图2引出的导线分别对MRD施加0、0.5、1.0、1.5、2.0、2.5 A的电流，研究在不同磁场强度下MRD的阻尼特性。将不同电流下力-位移关系转换为力-速度关系，结果如图4所示，其中横坐标表示MRD的输入速度v，纵坐标表示MRD的输出阻尼力F。

图2 实物图

图3 阻尼特性测试平台

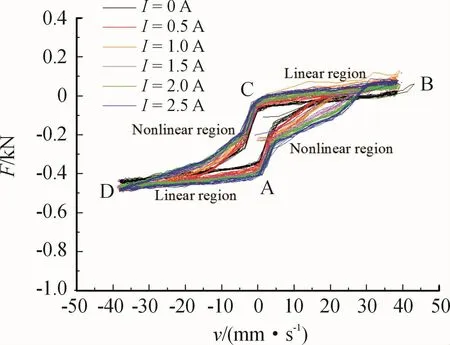
图4 不同电流下MRD力-速度关系

从不同电流下MRD的动态响应曲线可以看出，将速度换向处（A处和C处）和加速度换向处（B处和D处）作为分段点进行分段建模可将一个运动周期分为2段线性曲线和2段为非线性曲线。

2 Bingham模型中MRF力学特性

MRF在无外加磁场的影响下可近似为牛顿流体，此时MRF的剪切应力与剪切应变率之间的关系为：

式中：τ为剪切应力；η为黏度系数；γ为剪切应变率。

MRF在外加磁场影响下具有黏塑性流体特性，如图5所示，在不同的磁场强度下，流动模式可分为屈服前区、屈服区、屈服后区等3种变化过程。其中MRF在屈服前区剪切应力随剪切应变率的变化呈正相关；在屈服区剪切应力随剪切应变率的变化呈不稳定状态；在屈服后区呈稳态，剪切应力不随剪切应变率变化。

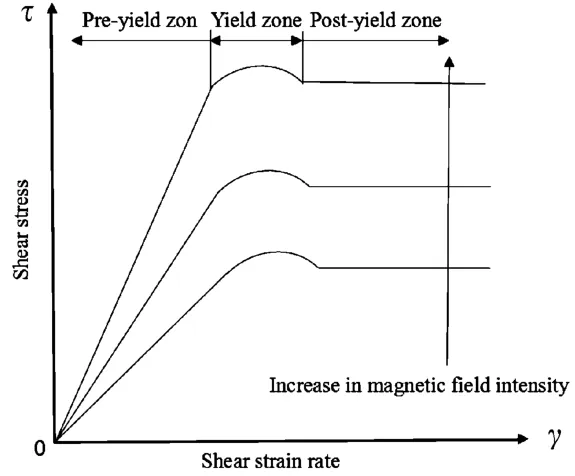
图5 MRF的剪切应力与剪切应变率关系

出于本文的实际工况及MRD的工作状态考虑，选取稳态工作状态下MRD中MRF的所处状态进行研究，此状态下MRF稳定流动处于屈服后区，剪切应力为定值，MRF黏度为定值。

Bingham模型将MRF的剪切应力描述为：

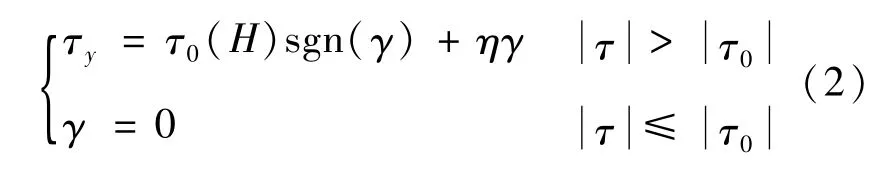
式中：τy为MRF的剪切应力；τ0为MRF的临界剪切应力；H为MRF所处磁场强度；γ为MRF的剪切应变率；η为MRF达到屈服后区的黏度系数。

Bingham模型中MRF在不同磁场强度影响下剪切应力与剪切应变率的量纲为一化关系如图6所示。

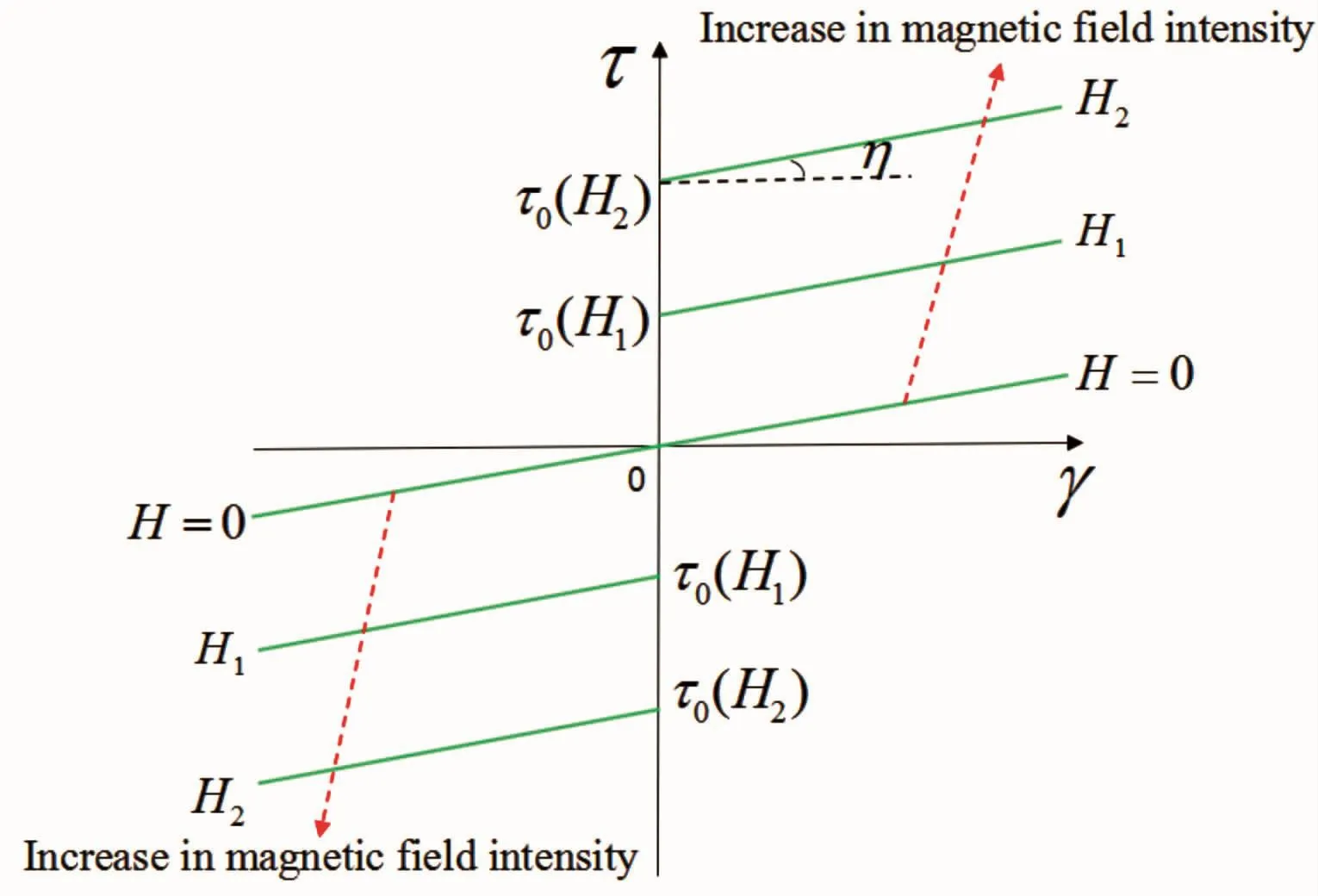
图6 Bingham模型中MRF本构关系

由图6可知，磁场强度的变化会改变Bingham模型中的临界剪切应力，而MRF在剪切屈服前后的黏度η在Bingham模型中被视为定值。

描述MRD输出力与激励速度之间线性关系的常用 Bingham力学模型，是由 Stanway等［38］提出的由库伦摩擦力和黏滞阻尼器构成的理想化模型，即：

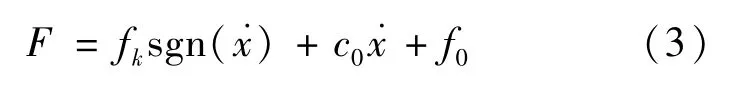
式中：fk为库伦阻尼力，与MRF的屈服应力相关；x为MRD的输出位移；˙x为MRD的输出速度；c0为黏滞阻尼系数；f0为补偿元件存在而产生的力，结合本文MRD实际结构及实际工况此项可忽略。

将图4的实验结果与Bingham力学模型进行对比分析，可以发现：图4的线性部分在理论上近似表示MRF达到屈服后期且黏度不变时MRD的运动状态，可通过Bingham模型模拟，但其非线性区域的滞回特性无法用Bingham模型进行精确描述。本文针对Bingham模型对描述MRD非线性区域力学特性存在的局限性问题，对传统的Bingham模型进行改进，从而获得更准确的磁流变阻尼器非线性力学模型。

3 力学建模与参数辨识

本文在Bingham模型基础上进行分段建模，对图4的线性部分采用Bingham模型，非线性部分分别采用多项式函数和Rational函数进行描述。

3.1 多项式-Bingham模型建立与参数辨识

对图4进行分析可知，B-C段和D-A段所表示的MRD输出力与速度之间的线性关系可通过Bingham模型进行描述，为了在形式上进一步简化分段模型，本文将式（3）中fksgn（˙x）视为一个整体 f，c0视为 c，则参数 f和 c为待识别参数。A-B段和C-D段为非线性部分，首先采用多项式函数进行描述。为了防止高阶振荡失真和更好地描述滞回特性，拟采用3次多项式建模，可得多项式-Bingham模型（以下简称为多项式函数模型），其表达式为：

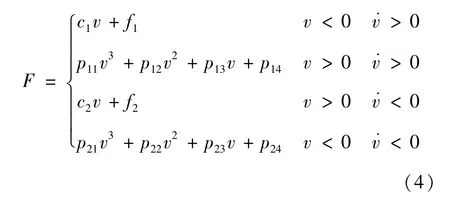
式中：v为MRD的速度；˙v为MRD的加速度；c1、f1、p11、p12…为待识别参数；式（4）中函数分别依次对应表示图4中D-A段、A-B段、B-C段、CD段。

本文采用最小二程曲线拟合法对模型参数进行辨识，最小二成曲线拟合法的基本原理是对给定数据（xi，yi）（i＝0，1，…，n），在函数类 φ中，求得g（x）∈φ，使误差的平方和R最小，可表示为：

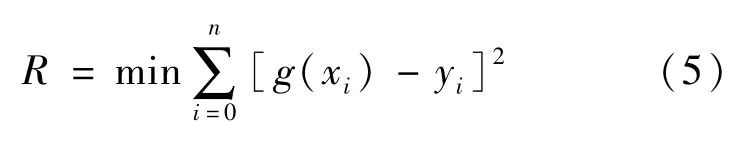
从几何意义上来说，就是找到与给定点（xi，yi）（i＝0，1，…，n）的距离平方和为最小的函数曲线 y＝g（x），函数 g（x）称为最小二乘解或拟合函数，求拟合函数g（x）的方法称为最小二乘曲线拟合法。

在振幅为2 mm、频率为3 Hz的振动工况下，将加载电流分别为 0、0.5、1.0、1.5、2.0、2.5 A的实验结果分别对多项式函数模型进行参数辨识，得到不同电流下对应的参数值，并建立不同参数与电流之间的关系。具体过程以加载电流为1.5 A的参数辨识结果为例，利用Matlab拟合工具箱对 CD段系数为 p21、p22、p23、p24的多项式函数进行曲线拟合，拟合结果如图7所示，可得CD段的各参数 p21、p22、p23、p24分别为：0.000 016、0.001 25、0.035 35、0.063 13。

根据拟合结果可以看出，多项式函数与实际散点之间的拟合偏差较小，因此三阶多项式具有一定的有效性。通过对多项式函数模型进行参数辨识，可得到不同电流下多项式函数模型的各参数值，部分结果如表1所示。

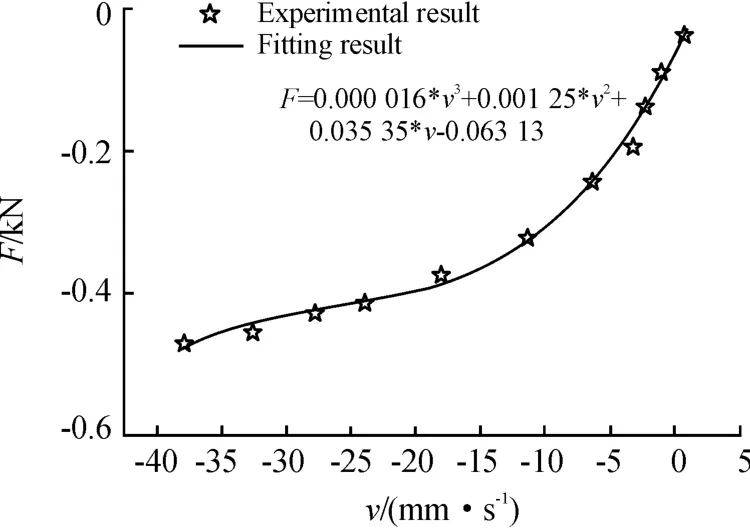
图7 1.5 A电流下C-D段多项式函数的拟合结果

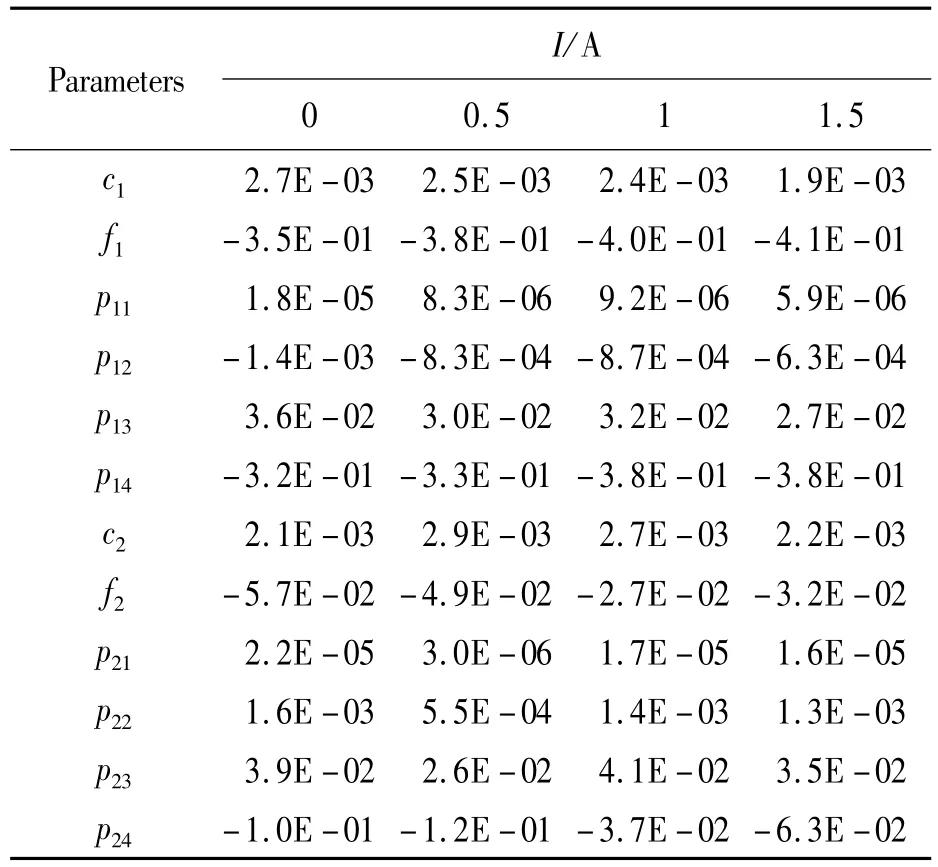
表1 多项式-Bingham模型参数辨识结果

通过对参数辨识结果进行分析可知，多项式函数模型各参数与电流之间为非线性关系，作者拟采用三阶多项式来建立各个参数与电流之间的关系，可得到各参数与电流的函数关系，部分结果如下：

以上为多项式函数模型中各参数与电流之间建立的映射关系，结合式（4），可以得到完整的多项式函数模型，其中模型的输入分别为电流和速度，输出为对应输入电流和速度下的输出阻尼力。

3.2 Rational-Bingham模型建立与参数辨识

为了更好地描述同一振动工况不同电流下MRD的动态响应，本文建立了有理函数模型与多项式函数模型表进行对比研究。本质上有理函数（rational函数）是由2个多项式的商表示的函数，表示如下：

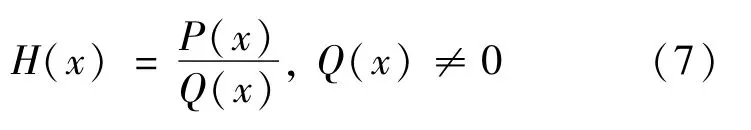
式中：P（x）为分子多项式函数；Q（x）为分母多项式函数。

当多项式拟合效果不够好时，Rational函数拟合在精度上有一定的优越性［39］。为了减少模型参数，将Rational函数的分子分母拟采用一次线性函数进行建模，可得到Rational-Bingham模型（以下简称为Rational函数模型）为：

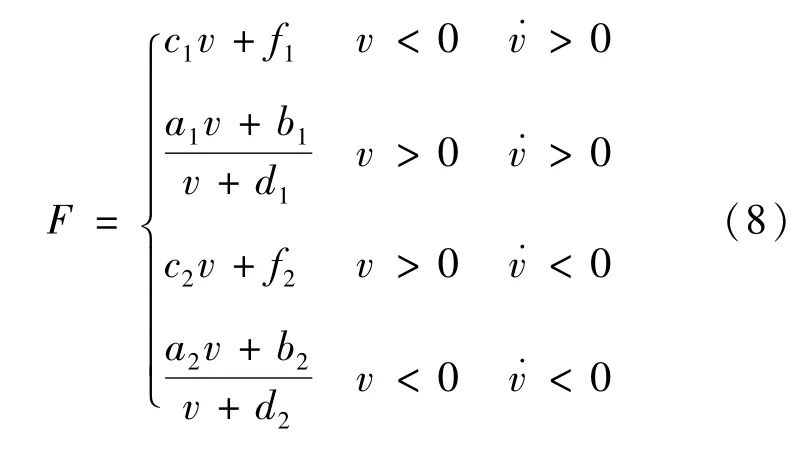
式中：v为MRD的速度；˙v为MRD的加速度；a1、b1、d1、a2、b2、d2为待识别参数；式中函数分别对应表示图4中 D-A段、A-B段、B-C段、CD段。

同样在振幅为2 mm、频率为3 Hz的振动工况下，将加载电流分别为 0、0.5、1.0、1.5、2.0、2.5 A实验结果分别对Rational函数模型进行参数辨识，得到不同电流下对应的参数值，并建立不同参数与电流之间的关系。具体过程仍以加载电流为1.5 A的参数辨识结果为例，利用Matlab中的拟合工具箱对CD段系数为a2、b2、d2的Rational函数进行曲线拟合，拟合结果如图8所示，可得CD段的各参数 a2、b2、d2分别为：-0.591 7、0.677 1、-11.78。

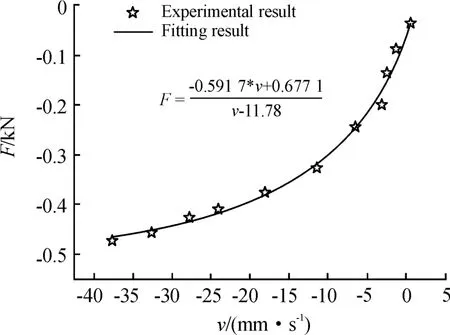
图8 1.5 A电流下C-D段Rational函数的拟合结果

根据拟合结果可以看出，与多项式函数模型相比，Rational函数模型与实际散点的拟合效果好一些，通过对Rational函数模型进行参数辨识，得到不同电流下Rational函数模型中各参数值，部分结果如表2所示。

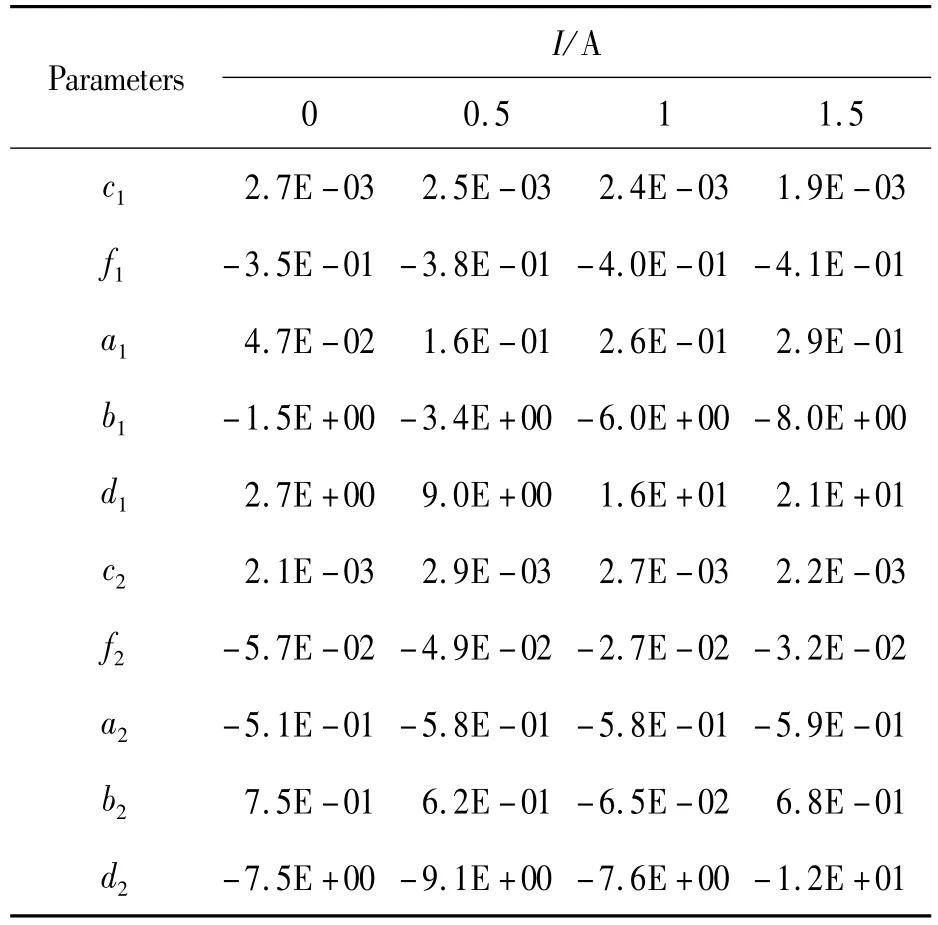
表2 Rational-Bingham模型参数辨识结果

同样，对Rational函数模型参数辨识结果进行分析可知，各参数与电流为非线性关系，选择采用三阶多项式来建立各参数与电流之间的关系，得到各参数与电流之间的函数关系，部分结果如下：

以上为Rational函数模型中各参数与电流之间建立的映射关系，结合式（8）可得到完整的Rational函数模型，与多项式函数模型相似，Rational函数模型的输入分别为电流和速度，输出为对应输入电流和速度下的输出阻尼力。

4 模型仿真分析

本文在Matlab／Simulink环境中对模型在不同工况下力与速度之间的非线性关系进行仿真分析。如图9所示，模型输入分别为可以自定义的输入电流及正弦位移激励，模型输出为MRD输出阻尼力与速度之间的关系。其中SubSystem模块中分别为多项式函数模型和Rational函数模型，是仿真系统的子系统。系统可分别输出在不同工况下多项式函数模型和Rational函数模型的F-v仿真结果。

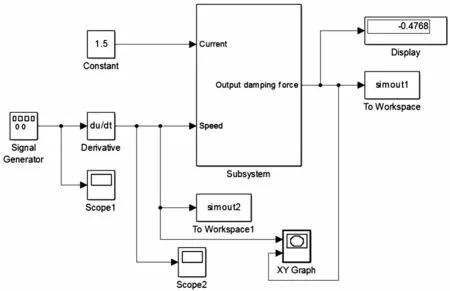
图9 模型的Simulink仿真框图

4.1 辨识工况（电流不同）

在振幅A为2 mm、频率f为3 Hz的振动工况下，将不同电流分别输入多项式函数模型仿真系统和Rational函数模型仿真系统，可分别得到输出F-v曲线并与实验结果生成对比，受篇幅限制，本节以施加电流大小分别为0、0.5、1.0、1.5 A为例，所得结果如图10所示。

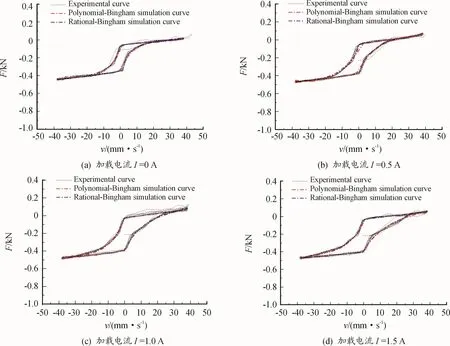
图10 辨识工况下两模型仿真结果与实验结果

通过分析图10中模型仿真结果与实验结果对比，可以得出以下结果：

1）从整体上看，在同一振动工况不同电流下2种模型的拟合效果都比较好，都可以不同程度较为准确地描述经典Bingham力学模型无法模拟的非线性滞回区域。

2）从局部上看，多项式函数模型在低于0.5 A时高速段存在局部不稳定性、在速度换向处存在拟合效果不佳的缺陷，而Rational函数模型可以修正多项式函数这一缺陷，在稳定性上更加符合实际。

4.2 验证工况（激励频率、振幅不同）

为了分别检验2种模型在同一电流不同振动工况下的适用性，将图9中输入电流设为I＝1.0 A固定不变，首先改变输入正弦位移激励信号的频率，以振幅A为2 mm、频率f为5 Hz为例，所得多项式函数模型和Rational函数模型的仿真结果与实验结果对比如图11所示。

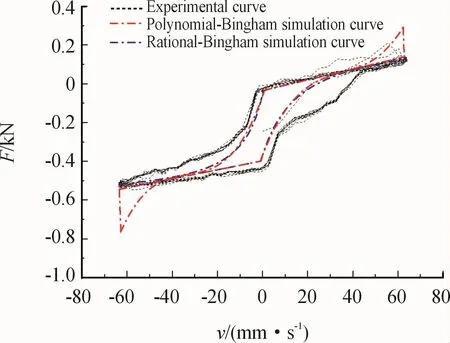
图11 I＝1.0 A，A＝2 mm，f＝5 Hz工况下，两模型仿真结果与实验结果

电流I＝1.0 A固定不变，改变输入位移激励信号的振幅，以振幅A为4 mm、频率f为3 Hz的振动工况为例，所得多项式函数模型和Rational函数模型的仿真结果与实验结果如图12所示。

通过分析改变正弦激励输入信号的频率或振幅后，2种模型的仿真结果与实验结果对比（见图11、图12），可以得出以下结果：

1）多项式函数模型存在的缺陷更加显著，改变频率或振幅后，多项式函数模型在一个行程周期的高速段均存在不收敛的现象。线性区的仿真结果趋近于实验结果，非线性低速区的仿真结果存在一定程度的误差。

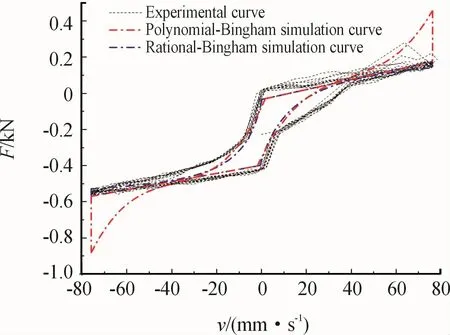
图12 I＝1.0 A，A＝4 mm，f＝3 Hz工况下，两模型仿真结果与实验结果

2）为解决多项式函数模型在改变振动工况后高速段存在不收敛问题，可将多项式函数与线性函数相交之后的高速段取线性函数，低速非线性区用多项式函数来表达，这将改变分段模型的分段方式，因此多项式函数模型在本文的分段方式下对同一电流不同振动工况的适用性较弱。

3）在改变频率或振幅后，Rational函数模型在非线性区的表达存在不同程度的误差，但总体仿真结果与实验结果相符，改变振动工况后仍然可以较好地模拟MRD输出阻尼力的最大值。此外Rational函数模型可以修正多项式函数模型高速段不收敛的震荡现象，对同一输入电流不同振动工况下的适用性较强。

2种模型的非线性区均存在一定程度误差的原因是：不同振动工况（正弦输入信号）直接影响模型的输入速度，所以简化模型中各参数与正弦输入信号的关系，在同一振动工况下建立各参数与电流之间的绝对关系，使得改变振动工况后非线性低速区的仿真结果存在一定程度的误差。

5 模型误差对比评估

2种非线性模型与实验结果之间的误差可通过均方根误差RMSE来进行评价，计算公式如下：

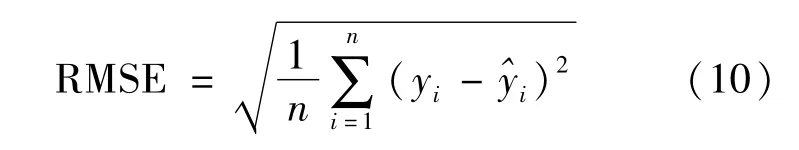
式中：RMSE为均方根误差；yi为拟合数据为实验数据。

5.1 辨识工况

对同一振动工况（A＝2 mm，f＝3 Hz）不同电流下，2种模型的仿真结果与实验结果各段的均方根误差值及Rational函数与多项式函数相比Rational函数的误差降低率，如表3所示。

CRMSE（累积均方根误差）计算公式表示为：

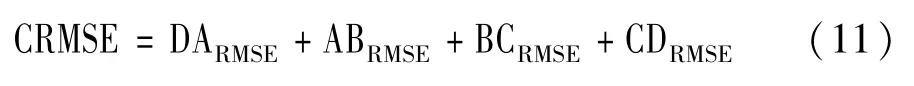
ERR（误差降低率）计算公式表示为：

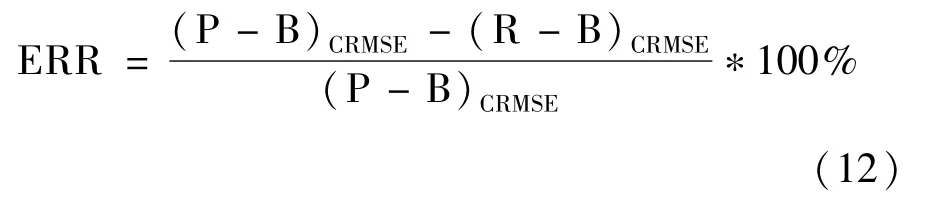
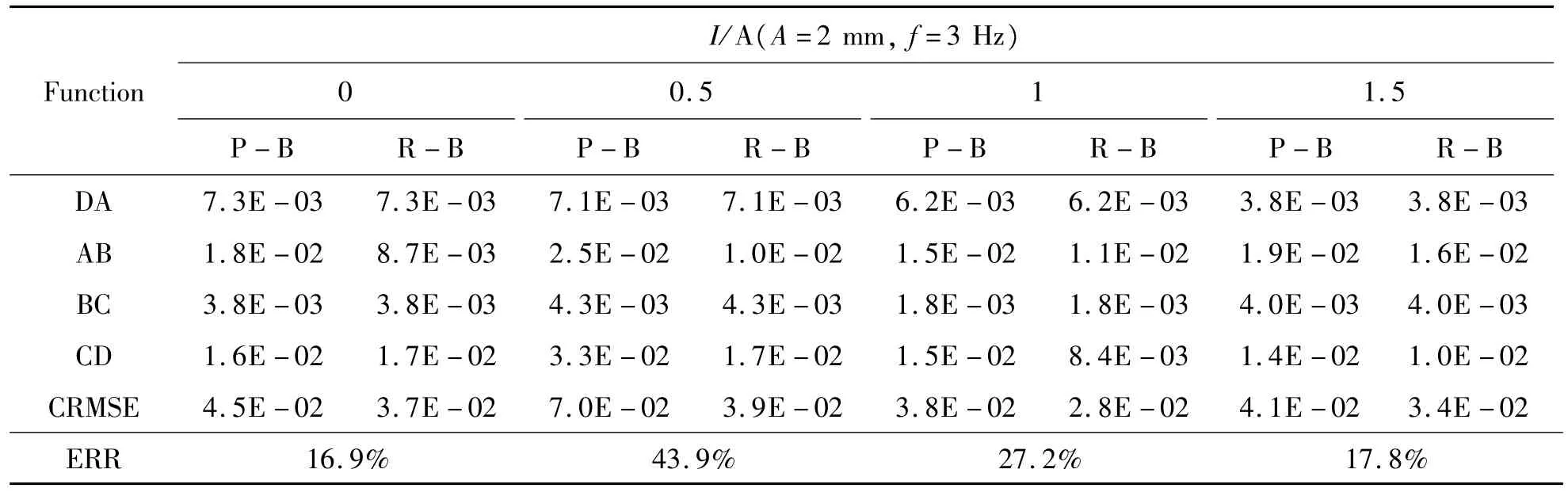
表3 2种模型在不同电流下的均方根误差

通过对表3进行分析，可以得出以下结果：

1）2种模型在同一振动工况不同电流下各段的拟合精度平均可达0.99以上；

2）不同电流下，Rational函数模型的累积拟合误差与多项式函数模型的累积拟合误差相比均有一定程度的降低，与2种模型各自的仿真结果一致；

3）在电流低于0.5 A时，Rational函数模型的误差降低率随着电流的增大而增大，电流高于0.5 A后Rational函数模型的误差降低率随着电流的增大而减小。

5.2 验证工况

对同一电流（I＝1.0 A）不同振动工况（分别改变正弦位移激励输入信号的频率和振幅）下，2种模型的仿真结果与实验结果各段的均方根误差值及Rational函数模型与多项式函数模型相比Rational函数模型的误差降低率，如表4所示。

通过对表4进行分析，可以得出以下结果：

1）2种模型线性区的误差结果较为接近，与模型结构相符合；非线性区多项式函数模型的误差与Rational函数模型相比均有不同程度的增大，与仿真结果一致；

2）同一电流不同振动工况下Rational函数模型与多项式函数模型相比Rational函数模型的误差降低率均在20%以上，结合图11、图12的仿真结果可知，Rational函数模型的适用性强于多项式函数模型。

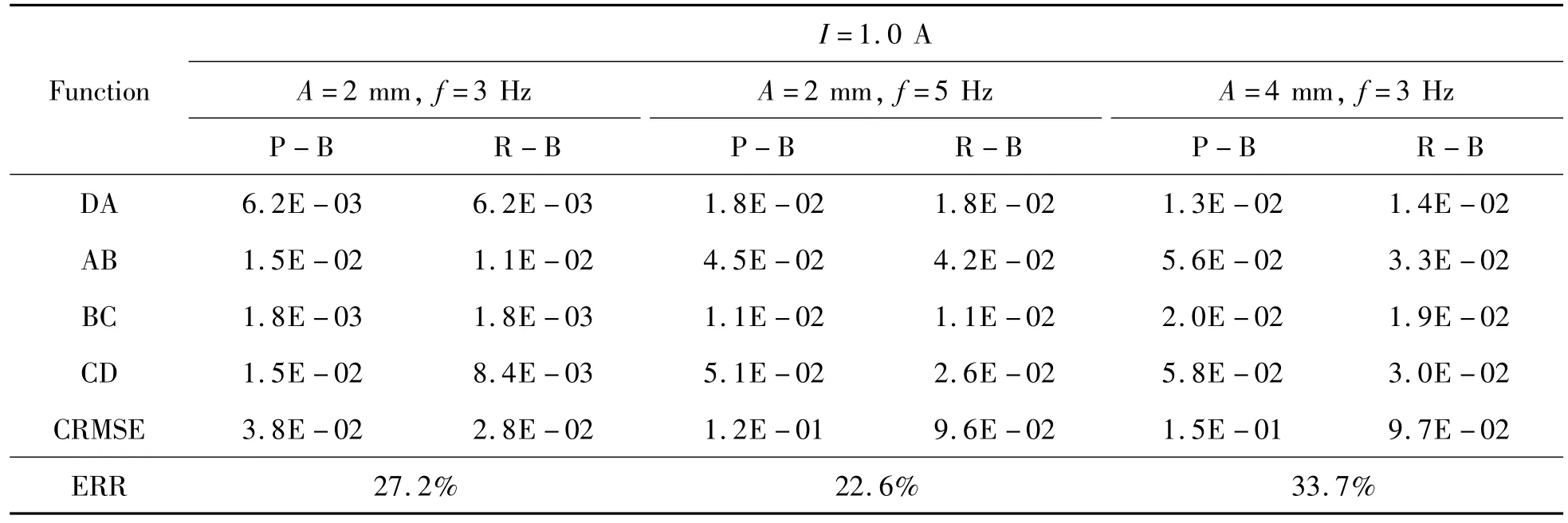
表4 2种模型在不同振动工况下的均方根误差

6 结论

1）相比于多项式函数模型，Rational函数模型的分子、分母项均为一次线性函数，模型参数较少，且模型结构简单，分段方式明确。

2）在相同振动工况下，Rational函数模型可改进多项式函数模型在电流低于0.5 A时高速段存在的不稳定性和在速度换向拐点处拟合效果不佳的现象，之后随着电流增大，2种模型拟合误差的差距逐渐缩小。Rational函数模型整体上可更加精确地描述MRD在不同电流下的非线性动态特性。

3）在相同电流下，改变输入正弦位移激励的频率或振幅，通过不同频率、不同振幅激励工况的验证表明，Rational函数模型与多项式函数模型相比，具有更高的精度和更好的适用性。