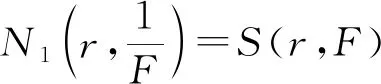涉及导数分担小函数的亚纯函数的唯一性
胡 岚,符方健,李 倩
(1.四川财经职业学院 通识与人文教育学院,成都 610000;2.琼台师范学院 理学院,海口 571127)
0 引言
本研究使用值分布论的基础知识及Nevanlinna常用理论的标准符号[1-2],其中:对于复平面上的亚纯函数f(z),其涉及到的符号S(r,f)表示任意满足S(r,f)=o{T(r,f)}(r→∞)的量,可能除去r的一个线性测度有限集合,且它每次出现并不一定相同。如果亚纯函数a(z)满足等式T(r,a)=S(r,f),那么称a(z)为f(z)的一个小函数。设f(z)与g(z)为复平面上的两个非常数亚纯函数,小函数a(z)称为亚纯函数f(z)与g(z)的CM(或IM)公共小函数,当且仅当在计重数(或不计重数)的情况下,f(z)-a(z)与g(z)-a(z)具有公共的零点。
用Ek(a,f)表示f(z)-a(z)的k(∈+正整数集)重零点(重级零点按其重数计算)的集合,Ek)(a,f)表示f(z)-a(z)的m(≤k)重零点的集合,即Ek)(a,f)=∪Em)(a,f)。E(k(a,f)表示f(z)-a(z)的n(≥k)重零点的集合。Ek(a,f)=Ek(a,g)表示f(z)-a(z)的k重零点当且仅当它是g(z)-a(z)的k重零点。用
分别表示相应集合Ek(a,f),Ek)(a,f)与E(k(a,f)的密指量
其中:
f(z)与g(z)权分担(a,k)表示f(z)-a(z)与g(z)-a(z)具有公共的零点,当m≤k时,若z*是f(z)-a(z)的m重零点当且仅当z*是g(z)-a(z)的m重零点;当时m>k,若z*是f(z)-a(z)的m重零点当且仅当z*是g(z)-a(z)的n(n>k且n不一定等于m)重零点。因此,f(z)与g(z)的IM或CM的公共小函数,可以表示为f(z)与g(z)的权分担(a,0)或(a,∞)。
定理A[2]2(Nevanlinna第一基本定理) 设f(z)为区间|z| 定理B[2]18(对数导数引理)设f(z)为复数域上的非常数亚纯函数,则 本研究主要利用值分布论的基础知识,将随机微分方程作为一种重要的数学工具(主要参考了文献[3-5]),探讨导函数的唯一性定理。 1964年,杨乐研究导函数的唯一性,得到了如下关于亚纯函数导函数的4CM值定理。 定理C[6]设f(z)与g(z)为复平面上两个超越亚纯函数,k为正整数,aj(j=1,2,3,4)为四个判别的有穷复数,若aj(j=1,2,3,4)为f(k)(z)和g(k)(z)的CM公共值,则f(k)=g(k)。 2012年,韩俊峰等人改进上面的结论,通过研究两个亚纯函数的k阶导数在涉及截断分担一个公共值的情况下得到了以下导函数的唯一性定理。 定理D[7]设f(z)与g(z)为复平面上的两个非常数亚纯函数,k∈+,aj(j=1,2,3,4)为四个判别的有穷复数,f(k)与g(k)分担a1,a2CM;f(k)与g(k)权分担(a3,1),E1(a4,f(k))=E1(a4,g(k))。若是则有f(k)=g(k)。 本研究将定理D中关于两个亚纯函数的导数分担公共值问题改进为分担公共小函数的情况,得到了改进的导函数的唯一性定理。 为了证明主要结果,需要引入以下引理。 引理1[8]设f(z)与g(z)为判别的非常数亚纯函数,aj(j=1,2,…,q)为f(z)与g(z)的q个互相判别的小函数,则对于任意的ε>0,有 其中:r∉E,E⊂R且ʃEdlog(logr)<∞。 引理2 设f(z)与g(z)为判别的非常数亚纯函数,aj(j=1,2,3)为f(z)与g(z)三个互相判别的小函数,如果aj(j=1,2,3)为f(z)与g(z)的IM公共小函数,那么有 S(r,f)=S(r,g)=S(r)。 证明由引理1可知 由此可得引理2。 引理3 设aj(j=1,2,3,4)为非常数亚纯函数f(z)与g(z)的四个判别的IM分担小函数,如果f(z)≢g(z),那么有 证明由引理1与引理2可知 即T(r,f)≤T(r,g)+S(r)。同理可得T(r,g)≤T(r,f)+S(r)。故有 T(r,f)=T(r,g)+S(r)。 由定理A与上式可知 引理4[9]f(z)为一个非常数亚纯函数,若是aj(j=1,2)为f(z)与g(z)两个互相判别的小函数且 则有 定理1 设f(z)与g(z)为复平面上的两个非常数亚纯函数,k∈+,aj(j=1,2,3,4),为f(k)与g(k)的四个判别的公共小函数,f(k)与g(k)分担a1,a2CM;f(k)与g(k)权分担(a3,1),E1(a4,f(k))。若有则有f(k)=g(k)。 证明令 则由命题中条件可得: 由引理2可知 S(r,F)=S(r,G)=S(r)。 令 (1) (2) 因此由式(1)可见,在F(F-1)的零点处,Δ1解析;F的极点处,Δ1解析。故有 N(r,Δ1)=S(r) , (3) 从而由定理B可知 m(r,Δ1)=S(r) , (4) 由定理A、式(3)和式(4)式可知 T(r,Δ1)=S(r) 。 (5) 类似地,由式(2)可知,Δ2在F(F-1)的零点处解析,在F与G的单重极点处也解析。故有 (6) 由定理B可知 m(r,Δ2)=S(r) , (7) 故由定理A、式(6)和式(7)可知 (8) 可以断言Δ1≡0或Δ2≡0。事实上,如果假设有Δ1≢0且Δ2≢0成立。 注意到:如果z∞为F的p(≥2)重极点,且为G的q(≥2)重极点,则z∞为Δ1的零点。 当Δ1≢0时,有 (9) 当Δ2≢0时,有 (10) 由式(8)和式(10)可知 (11) 由式(9)和式(11)可知 当Δ1≡0时,也即 (12) 对式(12)积分可得 当Δ2≡0时,也即 (13) 由式(13)可知:∞为F与G的CM分担值,a为F与G的IM分担值。又因E1(a,F)=E1(a,G),故F与G的权分担为(a,1)。令 (14) 即 (15) 则由引理4可知 m(r,Δ3)=S(r)。 (16) 以下对Δ3分两种情况进行讨论。 (I)若Δ3≡0,则 情况1 当F≡G时就有f(k)=g(k)。 情况2 当有 (17) 成立时,由式(13)可知 (18) 由式(17)和式(18)可得 (19) 对式(19)进行积分可得 F=AG(其中A为非零常数)。 (II)若Δ3≢0,结合式(18)可知 由0,1,∞为F与G的CM分担值,可知0,1,∞为Δ3的解析点。 假设za为F-a的p重零点,且为G-a的q重零点,但不是a和a-1的零点和极点。不失一般性,不妨设p≤q,由式(14)可知:za为Δ3的右端第一个分式中分子的至少p+q-1重零点,为Δ3的右端第一个分式中分母的q重零点,为Δ3的右端第二个分式中分子的至少2p-1重零点,为Δ3的右端第二个分式中分母的p重零点。从而可知za为Δ3的至少p-1(≥0)重零点,故za不是Δ3的极点。 综合以上分析可得 N(r,Δ3)=S(r)。 (20) 由定理A、式(16)和式(20)可知 T(r,Δ3)=S(r)。 (21) 由F与G权分担(a,1)及式(15)可知:F-a的p(≥2)重零点,G-a的q(≥2)重零点均是Δ3的零点。由式(21)可知 (22) (23) 即可得到a为F与G的CM公共小函数。 设Z0为F的m(≥2)重极点或F(F-1)的n(≥2)重零点,则z0为Δ3的零点。由式(21)可知 (24) (25) (26) 由引理3可知 (27) 由N1(r,F)=S(r)及式(22)—式(27)可知 (28) (29) (30) 令 因1与∞为F与G的CM公共值,故在F-1的零点处,α解析;在F的极点处,α解析。故有 (31) 由引理1可知 (32) (33) 由式(32)和式(33)可知 由上式可知 (34) 再由式(30)、式(31)和式(34)可知 N(r,a)=S(r), (35) 由此及定理B可知 m(r,α)=S(r), (36) 因此,由定理A、式(35)和式(36)可知 T(r,α)=S(r)。 (37) 若α≢0,设z1为F-1的1重零点,且为G-1的1重零点。则z1为α的零点。故由式(37)可知 (38) 若α≡0,则 对上式进行两次积分可得 (39) 又因0,a为F与G的CM分担,故A=1且B=1。由式(39)可知F=G,即f(k)=g(k)。 (40) (41) 因0,1,∞,a均为F与G的CM分担,故 N(r,H1)=S(r),N(r,H2)=S(r), (42) 由定理B可知 m(r,H1)=S(r),m(r,H2)=S(r)。 (43) 由定理A、式(42)和式(43)可知 T(r,H1)=S(r),T(r,H2)=S(r)。 (44) 若H1≢0,令z1为F-1的1重零点,且为G-1的1重零点,则H1(z1)=0。故z1为H1的零点。因此有 若H2≢0,令z0为F的1重零点,且为G的1重零点,则H2(z0)=0。故z0为H2的零点。这时也有 若H1≡0且H2≡0,由式(40)和式(41)可知 (45) 由式(13)和式(45)可得 a(1-a)(F-G)≡0。 (46) 又由于a≠0,1,故由式(46)可知F=G,即f(k)=g(k)。

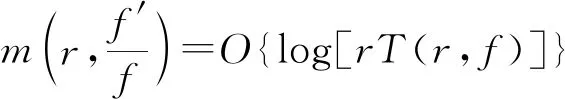
1 几个引理

2 主要结果及其证明