对资源导向型城市经济的简单模型分析
——以辽宁省本溪市为引
张林涛
(北京航空航天大学,北京 100191)
一、相对资本回报率与资源导向型经济的内在关联
几乎全部的资源导向型城市在其经济发展进入成熟乃至衰退期之前,矿产资源开发产业的发展速度都要快于其余产业。这种现象的一个突出表现是矿产资源开发产业的产出增长率高于其他产业的产出增长率。本文将以这一现象作为切入点,以进行模型的初步构建。
假设生产函数F=f(K,L)满足柯布道格拉斯生产函数的形式,也就是说,产出的增加或是因为生产技术发生变化,或是因为生产要素投入得到增加。由于生产技术发生变化带来的产量增长往往呈现断崖状,而我们看到的此类型增长十分平稳,因此这种增长的原因不在于生产技术而在于生产要素投入的增加[1]。对于钢铁以及其他的矿产资源开发产业,影响其产量的关键生产要素不是劳动力L而是资本K,因为高炉需要工人进行操作,但倘若不增加高炉数量而只增加工人数量则产量无法提高,因此劳动力的增加伴随于资本的增加,资本增加是关键。而资本的增加量等于矿产资源开发产业的投资减去折旧,即Ka=Is-R(Ka代表资本增加量,Is代表钢铁厂的投资,R代表折旧)。由于此时矿产资源开发产业的产出与生产规模不断扩张,可以得出其资本的边际产出大于折旧率这一结论,即MPK>rR(rR代表资本的折旧率),否则资源开发产业的生产规模则不能够继续提高。所以,此时就可以忽略折旧对资本增加带来的影响而只把投资视为改变资本增加量的唯一因变量(这表示只要投资增加资本存量就会增加,因为资本的边际产出在抵偿折旧的同时还有富余)。资源开发产业获得的投资越多,其资本增加量就越多,产出也就越多。
当把资源导向型城市视作一个宏观经济主体时,由国民经济恒等式Y=C+I+G(Y代表产出,C代表消费,I代表投资,G代表政府购买,NX净出口则不计入考虑,也就是视为封闭经济),我们可以得出Y-C-G=I,其中Y-C-G(即产出扣除消费与政府购买)被定义为国民储蓄,这里称为资源导向型城市的储蓄S。因此,我们最终可以得到一个关系式S=I,即资源导向型城市的所有投资都来源于储蓄,投资与储蓄相等。本文假定资源导向型城市的储蓄是既定的,因而投资总量也是固定的。本文构建的模型将投资I的用途设定为两部分,一部分是对矿产资源开发产业的投资Is,另一部分是对其余产业的投资Ie,即I=Is+Ie,也就是说资源开发产业(或者任意某种产业)的投资来自固定的总投资的一部分。下面,我们讨论的关键在于投资如何对这两个部分进行分配。为了帮助我们进行讨论,在此我们引入一个变量,投资分配系数a,表示对矿产资源开发产业(或者目前先视作任意某种要代入分析的产业)的投资占全部投资的比例,即Is=a×I。
由此,我们就构建起了一个可以用来分析资源导向型城市经济的初步模型。这一模型的核心要素是资源开发产业的相对资本回报率。我们目前通过相对资本回报率这一核心变量意图说明两个问题。其一,资源导向型城市的经济结构在最初是如何形成的,一个地区有充裕的自然资源或许并不足以使其形成资源导向型经济,关键在于自然资源开发相关产业是否能够具有相对较高的资本回报率。美国加州具有十分丰裕的自然资源,包括大量的石油、天然气、石棉、金、钨等,但是美国加州的经济结构并非形成以自然资源开发为支柱的资源导向型经济,资本回报率可能是一个原因。其二,不同资源导向型城市的经济结构的不同。不同资源导向型城市的区位越适合于发展资源开发型产业,资源开发型产业的资本回报率相较于其他产业越高,其支柱的资源开发产业占经济的比例就会越大。
二、索洛经济增长模型的引入
以基本的索洛经济增长模型为基础继续拓宽本文的模型。根据基本的索洛经济增长模型,生产函数Y=f(K,L),对各项除以L,得到Y/L=f(K/L,1),因此人均产出(Y/L)是人均资本(K/L)的函数,我们把这一函数写作y=f(k)。同时,索洛经济增长模型仍然满足基本的投资等于储蓄的关系式,且人均投资等于人均产出×储蓄率,即i=s×y=s×f(k)(s为储蓄率)。来源于储蓄的投资使资本增长而折旧使资本减损。在此基础上,索洛经济增长模型定义了一个稳态点,在这一点投资与折旧相等从而使资本数量稳定在该水平。稳态的人均资本数量为k*,其也代表了一个经济长期将达到的经济规模。图1即展现了索洛经济增长模型定义的稳态资本数量,图1中斜向上的直线代表折旧曲线,凸向于纵轴的曲线代表投资曲线,两者的交点k*即为稳态资本数量。

图1 索洛经济增长模型定义的稳态资本数量
接着引入之前构建的模型,由资源开发产业的投资与总投资的关系式Is=a×I(对资源开发产业的投资等于总投资×分配系数)可以得到人均对资源开发产业的投资等于分配系数a×人均投资i,即is=a×i。由此我们可以在图1中再加入一条资源开发产业的投资曲线,该曲线与折旧曲线相交于一点,定义该点为k1。该点表示了资源导向型经济中其资源开发产业的稳态资本数量,同时也表示资源开发产业占总体经济的规模(k1越靠近k*,资源开发产业占总体经济的规模就越大)。(见图2)在图1的基础上,虚线代表资源开发产业的投资曲线,原点到k1的距离Ok1表示资源开发产业的经济规模,原点到k*的距离Ok*表示总体经济规模,k1到k*的距离表示其余产业的经济规模。

图2 资源开发产业的投资曲线
当资源开发产业的相对资本回报率上升时,分配系数a会增加,同时资源开发产业的投资曲线会向上偏移(is=a×i,在k一定时,a增加,is也会增加),新的资源开发产业的投资曲线与折旧曲线相交于k2,k2>k1。这表示当资源开发产业的相对资本回报率上升时,其经济规模也会得到增加。(见图3)当我们假定规模报酬递增时,这个模型就能够帮助我们解释资源导向型经济的经济惯性现象。当初始时资源开发产业具有相对较高的资本回报率时,其会吸引大量投资使经济规模到达k1处,此时由于规模报酬递增,其会取得额外的资本报酬,因此提高了资本回报率,进而又吸引更多投资推动自身的经济规模达到k2处,这一过程一直持续直至规模效益被完全挖掘。因而,我们可以看到资源导向型经济往往越发展,其经济形态就越是依赖于资源开发产业,这一过程在下图中得到呈现(见组图4)。

图3 新的资源开发产业的投资曲线与折旧曲线
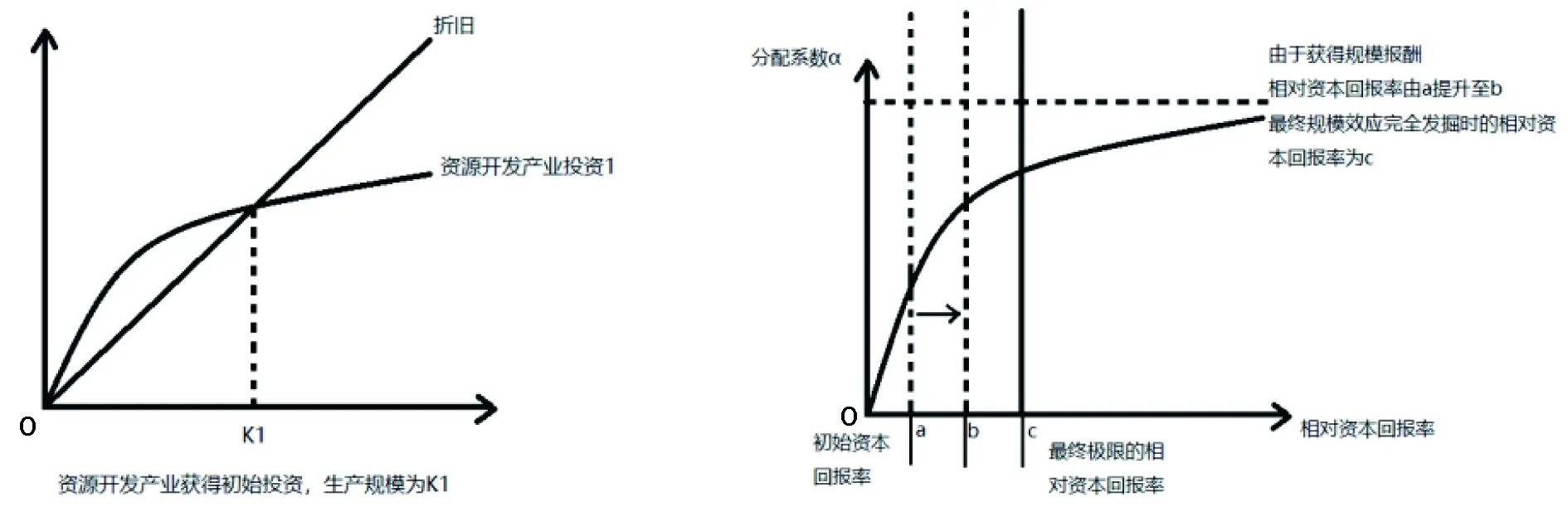
图4 规模报酬递增所影响图3所示的情形变动
到了这里,模型就已经基本构建完毕,并且也运用其解释了三个资源导向型经济中存在的基本问题。下面,本文将引出资源导向型城市在经济发展进入成熟以及衰退期后会出现的一个问题,该问题可由本溪市经济现象中观察到且也能够被我们构建的这一模型所解释,我们依据模型将其称为“折旧刚性”。
三、折旧刚性对资源导向型城市的影响
1.“折旧刚性”的概念分析
当一个地区的矿产开采出现枯竭时,资源开发产业的生产效率就会降低,表现为在相同的资本与劳动力情况下产量低于成熟期产量,因此其生产函数曲线会呈现出随着时间推移向内偏移的状态(资本劳动力不变但产量不断下降,从而形成由上到下的对应于不同时期的不同生产函数曲线)。生产函数曲线的下滑、生产效率的降低会导致资源开发产业的资本边际产出及相对资本回报率下降,进而导致分配系数a下降,最终使得资源开发产业的投资曲线降低。新的资源开发产业的投资曲线与折旧曲线相交于新的一点k3,k3小于资源出现枯竭前资源开发产业的稳态资本k1,亦即矿产枯竭带来的生产效率的降低会导致资源开发产业的稳态资本或者可以说经济规模下降。

图5 资源出现枯竭前后资源开发产业的状况
所以,当资源导向型城市的经济进入衰退期时,其资源开发产业的稳态资本或者也可以说有效的经济规模应该降至k3水平,并且随着时间的推移,矿产开发产业的生产效率进一步下降,倘若政府不进行干预,k3会远离原本的稳态资本k1而趋向于原点。这是我们由模型可以得到的结果。但是实际情况是,资源导向型城市中的资源开发产业往往在这种状况下也会维持在原本k1的规模下进行资本折旧,也就是说会出现k3k1的资本,其生产效率要低于其折旧成本,属于社会的“负资产”。此种现象即为“折旧刚性”,这一概念的提出是类比于宏观经济学的“工资刚性”,两者有相似之处。“折旧刚性”背后的力量来自于政府,而动因往往出自“就业”问题。
2.本溪市应对折旧刚性的策略及相关思考
位于本溪市的本溪钢铁有限公司(以下简称“本钢”)曾经经历过辉煌,是本溪市的代表企业。同时本钢作为国有企业基本垄断了本溪市的矿产资源开发,形成了非常大的体量规模,在本溪市几乎随处可以看到本钢的影子。不过自从2019年,本溪市的矿产资源短缺已经越来越严重,国内产能过剩极大冲击了钢材价格,导致本钢出现持续的亏损。目前,本钢每生产1吨钢铁要亏损约1000元。对于本钢来说,裁减员工关闭工厂似乎是最佳的选择,但是本钢并没有如此。其主要的工厂依旧在相对低效率的运行而员工也基本维持原编制。这背后的力量就在于本溪市政府出于对“就业”问题的考虑而给予本钢的生产补贴。
政府出于对社会问题的考虑就会给予资源开发产业的企业以生产补贴来弥补k3k1的投资,从而稳定就业,这就导致了“折旧刚性”的现象(当一个地区的资源开发产业被少数企业垄断时尤其如此),而“折旧刚性”会给资源导向型城市的经济带来不利的影响。
其一,在于政府负债问题,为了维持就业,政府需要扩大地方财政赤字来对资源开发产业进行补贴或者说是一种变相的投资。政府的投资量等于k3k1之间的距离。根据模型,随着资源开发产业的生产效率因为资源进一步枯竭而进一步下降,k3将继续远离k1。这意味着政府如果选择进行生产补贴,其就要承担一个逐渐走高的债务压力。倘若处理不当会产生经济波动等系统性风险。同时,很多文献研究认为,政府的支出对于引导资源导向型城市进行经济转型起到非常重要的作用[2]。过高的债务压力毫无疑问会削弱政府通过财政支出引导经济转型的能力。与此同时,政府的措施不能从根本上解决就业问题,就业问题的解决还要依赖于经济转型升级的实现。
其二,政府为了稳定就业采取生产补贴的方式,实际在投资一个社会的“负资产”。其资本的收益不足以抵偿折旧的成本,因此生产补贴实际是对社会福利的一种无谓消耗。同时,根据模型,由于投资总量是固定的,当政府的投资扩大时,私人的投资就会被挤出从而减少。一方面,政府不断增加带来负收益的投资;另一方面,很多具有更高效率的投资被挤出,从而导致原本低迷的经济雪上加霜。
四、结语
综上所述,首先,本文意图以相对资本回报率作为分析资源导向型城市经济现象的切入点,并依据基本的索洛经济增长模型构建起一个简单的用于分析资源导向型城市经济的模型。其次,运用这个构建起来的简单模型试图对有关资源导向型经济的三个问题给出答案。其一,一个地区为什么会发展为资源导向型经济。这个问题的关键不在于是否有丰裕的自然资源,而在于资源开发产业是否具有相对较高的资本回报率。其二,是什么从根本上影响了不同资源导向型城市,其主导产业部门占总体经济的比例。这一问题也可以从相对资本回报率中找到答案,资源开发产业具有越高的资本回报率,其占总体经济的比例就会越大。其三,如何理解资源导向型经济的“经济惯性”。模型对这一问题的解答关键在于规模报酬递增给分配系数a带来一种类似于“惯性”的变动趋势。最后,运用该模型,结合本溪市实际存在的经济现象,指出并试图分析一个存在于资源导向型城市的“折旧刚性”的问题。
本模型理论仍然存在很多局限,例如不能解释城市经济与资源开发产业的发展之间的联系,封闭经济的宏观经济假定偏离实际,等等。与此同时,现实的资源导向型经济的相关发展问题仍然十分复杂,因此该模型还不能深入完整地对各方面问题作出解释。因此,本文的主要目的是希望能够为有关问题的分析提供工具上的创新与帮助。

